一类求解全局优化问题的单参数填充函数算法
2022-09-30段晓辉景书杰牛海峰
段晓辉,景书杰,牛海峰
(河南理工大学 数学与信息科学学院,河南 焦作 454000)
1 引言
全局优化被广泛地应用于工程、运输、生产、经济等领域.全局优化方法可分为随机型方法和确定型方法两大类.前者包括模拟退火法[1]、遗传算法[2]、粒子群算法[3]等,后者包括打洞函数法[4]、填充函数法[5]等.本文主要讨论确定型方法中的填充函数算法,该算法的主要步骤是从目标函数任一局部极小点出发,构建一个与之相关的复合函数,通过极小化上述复合函数找到一个更好的局部极小点.填充函数算法的关键是构建满足条件的复合函数和选取有效的局部优化算法.上面构建的填充函数是一个与目标函数有关的复合函数且需要满足x′填充函数定义,局部优化算法通常根据问题类型从前人提出的经典局部优化算法中选择.构建有效可行的填充函数为该算法的关键.
1990年,葛仁普提出了求解无约束全局优化问题的填充函数法,给出了第一代填充函数P-function,具体见文献[6].上述填充函数存在许多不足,如:填充函数包含指数项,使得在计算中可能产生假的平稳点.为了改善上述不足,后续研究者提出了新的填充函数及有效算法,如文献[7].
同时葛仁普在文献[6]中给出了原始填充函数定义.





2 准备工作
我们考虑如下优化问题:

(P)
其中X为有界闭集且X⊂Rn.
为了解决问题(P),首先假定目标函数满足如下假设:
(1) 函数f(x)在Ω上是连续可微的.
(2) 函数f(x)是强制性的,即函数f(x)满足

(3) 问题(P)的不同局部极小点的个数可以是无限的,但不同局部极小值只有有限个.
定义1.1[9]函数f(x,x*,P)称为f(x)在局部极小点x*处的填充函数,如果它满足下列条件:
(1)在X上x*是F(x,x*,P)的一个严格局部极大点;
(2)对于任意的x∈S1,有▽F(x,x*,P)≠0.即F(x,x*,P)在S1上没有极小点或鞍点,其中
S1={x∣f(x)≥f(x*),x∈X{x*}};
(3)如果x*不是f(x)的全局极小点,那么F(x,x*,P)在S2上一定存在局部极小点,其中S2={x∣f(x) 本文构造问题(P)的一类填充函数: ψ(f(x)-fx*)) (2.1) 下面证明当参数A充分大时,函数F(x,x*,A)为满足定义2.1的填充函数. 定理3.1设x*是问题(P)的局部极小点,则当A充分大时,x*是F(x,x*,A)的一个严格局部极大点. 证明当x=x*时,代入(3.1)可得: 由于x*是问题(P)的局部极小点,从而 ∃δ>0,对∀x∈N(x*,δ)且x≠x*,有 f(x)≥f(x*),即f(x)-f(x*)≥0. φ(A·(f(x)-f(x*)))=2,ψ(f(x)-f(x*))=0代入(3.1)有 综上所述,当A充分大时,x*是F(x,x*,A)的严格局部极大点. 定理3.2设x*是问题(P)的局部极小点,则当A充分大时,对于任意的x∈S1,有▽F(x,x*,P)≠0,其中S1={x∣f(x)≥f(x*),x∈X{x*}}. 证明对∀x∈S1={x∣f(x)≥f(x*), x∈X{x*}}有f(x)-f(x*)≥0且x≠x*,取 定理3.3若x*不是问题(P)的全局极小点,则函数F(x,x*,A)在S2上存在局部极小点,这里 S2={x∣f(x) 证明令S3={x∣f(x)≤f(x*),x∈X},记∂S2={x∣f(x)=f(x*),x∈X},则S3=S2∪∂S2,且S3及∂S2均为有界闭集. (1)因为∂S2为有界闭集,且F(x,x*,A)为连续可微函数,故∃x′∈∂S2为函数F(x,x*,A)在∂S2上的全局极小点,因此 F(x′,x*,A)=minx∈∂S2F(x,x*,A)=0. (2)对∀x″∈S2,φ(A·(f(x)-f(x*)))=0,代入(3.1)可得 f(x*))=-(f(x″)-f(x*))2+(fx″)-f(x*))3<0. 综上所述,若x*不是问题(P)的全局极小点,函数F(x,x*,A)在S2上存在局部极小点. 本节中,结合上面构建的填充函数给出下述算法. 步骤0 初始化阶段 选择Up作为A的上确界(本文中取UA=109); 选择常数ρ>1(本文中取ρ=103);选择初始值A=1;选择初始值A=1;提前给出方向向量记为di,i=1, 2, …,2n.任取点x0∈X作为极小化问题(P)的初始点;令k=1,转步骤1. 步骤2 构建填充函数如下: ψ(f(x)-f(x*)). 步骤5 若A 对上述算法做如下注解: (1)本文在数值计算中步骤1中选择用FMINCON函数极小化目标函数;步骤4中选择BFGS拟牛顿算法极小化填充函数. (2)初始化中方向向量di如下: 例1 (二维函数) minf(x)=[1-2x2+csin(4πx2)]2+[x2- 0.5sin(2πx1)]2 s.t.0≤x1≤10, -10≤x2≤0. 其中c=0.2, 0.5, 0.05.对所有c全局极小值为f(x*)=0.具体迭代过程见表1. 例2 (三驼峰函数) s.t.-3≤x1≤3, -3≤x2≤3. 全局极小点为x*=(0, 0)T.具体迭代过程见表2. 表1 例1的数值实验结果(c=0.05) 表2 例2的数值实验结果 例3 (n维正弦平方Ⅱ函数) s.t.-10≤xi≤10,i=1, 2,…,n. 表3 例3的数值实验结果(n=10) 表4 数值实验结果对比 上述表1—表3中的数值结果,证明本文中构建的填充函数及算法是有效可行的.表4的数据说明在初始点相同的情况下,与文献[10]结果比较本文算法迭代次数更少或结果更精确. 本文在不含有不等式约束条件下构建了新的只含有一个参数连续可微的填充函数,且在适当条件下该填充函数与目标函数含有相同的局部极小点,因此可以减少极小化目标函数的次数,在一定程度上加快了计算速度.从理论上证明提出的函数满足填充函数定义,设计相应的填充函数算法,结合MATLAB软件通过数值实验证明算法是可行的.3 新的填充函数
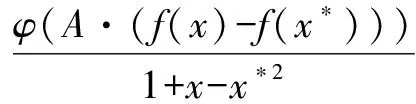








4 算法和数值实验结果
4.1 填充函数算法


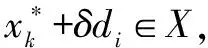


4.2 数值实验及结果





5 结语
