海上供应船的周期性调度与规划

侯春媛，钟铭，岳美

(大连海事大学交通运输工程学院，辽宁 大连 116026)

0 引 言

许多石油和天然气生产商运营着海上设施。因为海上设施空间有限，所以需要定期进行补给，以保证海上设施生产活动的正常进行。对于海上设施的补给需要专门的船将所需物资从陆上供应基地运送到海上设施。这种在供应基地与海上设施之间来回运输补给的船舶即为供应船。在海上供应链中，供应船是一种非常昂贵的资源，一艘供应船的日租金可达数万美元。因此，为提高供应服务的成本效益，对供应船进行规划是非常有必要的。供应船规划问题(supply vessel planning problem, SVPP)包括确定最优的船队组成、确定规划期内各供应船的航线和时间表(即供应船的船期表)。船期表的有效期取决于何时出现新的需求或者需求发生巨大的变化(例如，新的勘探钻机需要进行维修，或者某海上设施的主要作业从钻井改为生产，或者其作业从钻井和生产改为仅生产)，一般为几个月。SVPP的目标是最小化运营成本，同时保持可靠的供应服务，要尽量减少的费用是供应船的定期租船费用(固定成本)和航行费用(可变成本)。供应船的一次航行起止于陆上供应基地，且供应船在一次航行中访问一个或多个海上设施。

SVPP是一个船队组成和周期性的路线问题，与车辆路径问题(vehicle routing problem，VRP)相似。DANTZIG等最早提出VRP，并基于线性规划给出该问题的求解过程。

SVPP虽然与VRP有许多相似之处，但也有其自身的特性，如在规划期内需要多次访问海上设施。目前，研究SVPP的文献较少。BORTHEN等提出一个针对SVPP的双目标模型及其遗传搜索求解方法，使规划人员能够同时考虑成本和与持久性相关的目标。NORLUND等提出一种多步骤模拟优化方法，生成能同时考虑成本、排放和鲁棒性等3个因素的规划期供应船计划。KISIALIOU等引入优化与仿真相结合的鲁棒方法，在生成船舶交货时刻表时考虑特定航程的鲁棒性。BORTHEN等提出一种基于混合遗传搜索和自适应多样性控制的元启发式算法，成功地解决了多周期的VRP。CUESTA等研究了一艘船的装卸和交货问题，即单艘船在一组海上石油平台上执行装卸和交货操作，并涉及订单选择。HALVORSEN-WEARE等提出一个新的弧流模型和一个基于航行的模型来解决SVPP。KISIALIOU等研究了具有灵活出发时间和多类型船舶的周期性供应船规划问题，并开发了一个自适应大邻域搜索算法对其进行了求解。MAISIUK等提出一个离散事件模拟模型，以评估考虑不确定性天气条件和未来现货船费率的船队规模配置，并利用实际算例对模型进行了验证和测试。HALVORSEN-WEARE等考虑海上供应船服务中出现的船队组成和周期路径问题，提出一种基于航次的求解方法。NORLUND等开发了一个模拟优化工具，用于估计在各种天气条件下船舶在规划期内的平均燃料消耗，并生成在不同天气条件下的航次，提高了在环境目标与成本目标之间进行优先权衡来生成船期表的可行性。NORLUND等通过优化航行速度来减少供应船在海上设施供应服务中的排放，并介绍了几种用于船舶周期调度的速度优化策略。

综合分析以上文献可知，现有解决SVPP的方法主要为求其近似解的启发式算法，不能保证解的质量。本文在现有研究的基础上，考虑各海上设施需要访问的次数、供应基地和供应船容量约束、船舶均匀离港等因素，以最小化运营成本为目标，建立海上供应船调度与规划模型；运用分支定价算法对模型进行求解，并提出一种生成船期表的方法；通过算例分析证明算法和模型的合理性与有效性。

1 问题描述

SVPP既可作为确定性问题求解，也可以作为随机问题求解。确定性供应船规划意味着参数值不随时间动态变化，不受不确定因素(比如不确定天气条件)的影响。本文研究确定性SVPP。

=∪{0}∪{+1}为所有网络节点的集合，其中为海上设施集合，={1,2,…,}，0代表陆上供应基地，+1代表虚拟陆上供应基地；=∪{0}；+1=∪{+1}；={(,)|,∈,≠}为弧集；={,}为供应网络集合；为海上设施集合的包含任意个海上设施的真子集，即⊂；为航次集合，∈；为供应船类型集合，∈；为型供应船的数量；为型供应船的容量；f,为型供应船的固定成本；,,为型供应船从海上设施到的可变成本；为供应基地第天的服务能力；和分别为航次最短和最长持续时间；为在供应船的一次航行中所访问海上设施的货物需求量；s,为服务海上设施的时间；为一个规划期内海上设施所需的访问次数；,,为型供应船从海上设施到的航行时间；为规划期，其中∈。,,和,,为决策变量：型供应船经过弧(,)时,,为1，否则为0；型供应船在第天开始航次时,,为1，否则为0。

2 模型及算法

2.1 模型建立

SVPP的目标是在保证可靠的供应服务的情况下使运营成本最小化。通常石油公司通过定期租赁供应船进行供应服务，并确定规划期内的船期表，该计划通常在几个月内是有效的。因此，本文给定海上设施在规划期内的总需求。由于海上设施空间有限，供应船规划还需要满足海上设施在规划期内所需的访问次数，则每次访问海上设施的需求为总需求除以访问次数，且对于任一航次，供应船所访问的海上设施的总需求量不应超过其容量。根据SVPP区别于VRP的特性，本文模型考虑在规划期内需要访问海上设施的次数、供应基地和供应船容量约束、船舶均匀离港等，并采用由Dantzig-Fulkerson-Johnson提出的方法(简称DFJ法)来消除航次内的子回路。模型目标函数包含固定的定期租船成本和可变的航行成本两部分，具体描述如下：

(1)

(2)

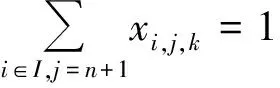
(3)

(4)

(5)

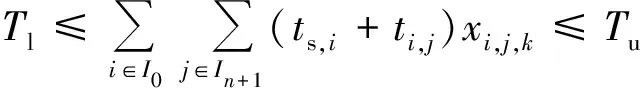
(6)

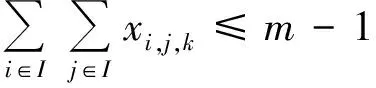
(7)

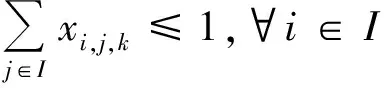
(8)

,,∈{0,1}

(9)

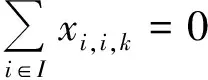
(10)

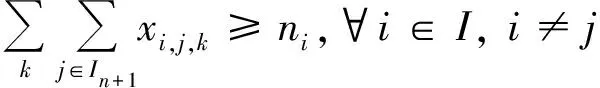
(11)

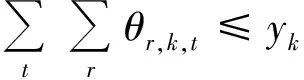
(12)

式(1)表示目标函数为航行的固定成本和变动成本的总和最小；式(2)和(3)表示在规划期内各供应船必须从陆上供应基地出发并返回到虚拟陆上供应基地；式(4)为流量守恒约束，表示到达和离开同一海上设施的弧的数量必须相等；式(5)表示供应船的装载量不得超过其容量；式(6)表示一个航次的持续时间约束；式(7)表示采用DFJ法消除任意一个包含任意个海上设施的子回路；式(8)表示任意一个航次访问一个海上设施最多只能有一次；式(9)表示变量约束；式(10)表示同一航次供应船不能连续访问同一个海上设施；式(11)表示必须保证海上设施在规划期内所需的访问次数；式(12)表示可用型供应船的数量约束。

船期表和均匀离港是由给定的海上设施在规划期内需要的访问次数决定的。用、和分别表示在规划期内需要访问2次、3次和4次的海上设施集合，则船期表和均匀离港约束如下：

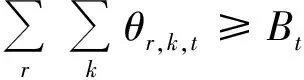
(13)

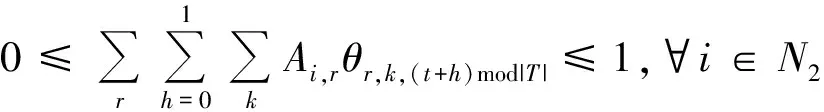
(14)

(15)

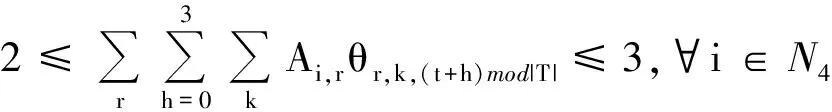
(16)

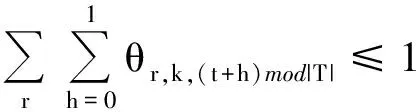
(17)

,,∈{0,1}

(18)

将决策变量，，中的用(+)mod||代替就为式(14)～(17)中的，,(+)mod||，其中(+)mod||表示(+)除以||的余数，||表示规划期的长度。式(13)表示陆上供应基地服务供应船的能力约束；式(14)确保在规划期内访问海上设施2次，在任何2天(=0,1)内最多有1次离开；式(15)确保在规划期内访问海上设施3次，在任何3天(=0,1,2)内至少有1次且不超过2次的离开；式(16)确保在规划期内访问海上设施4次，在任何4天(=0,1,2,3)内至少有2次且不超过3次的离开；式(17)表示任意连续2天同一艘船最多只能离开1次；式(18)表示变量约束。

2.2 算法设计

2.2.1 基本概念与流程

列生成算法可以快速求解大规模问题，但无法获得整数最优解；分支定界法虽然可以获得整数最优解，但对求解大规模问题乏力。DESROSIERS等于1992年提出分支定价算法，获得VRP的整数最优解。分支定价算法就是在分支定界法的基础上，采用列生成算法对每个分支进行求解。图1简要概括了分支定价算法的主要步骤。其中列生成算法的核心思想为：用单纯形法求解经过线性松弛后的主问题，用所得约束的对偶变量对子问题进行定价，并调用MATLAB的LPSolve工具箱对定价后的子问题进行求解，然后将对子问题求解所得的路径集作为新的列加入原有路径集中;再用单纯形法求解松弛后的主问题，得到新的后对子问题重新定价，并继续寻找有效路径集；如此迭代，直到无法找到有效路径，即获得了松弛后主问题的最优解。

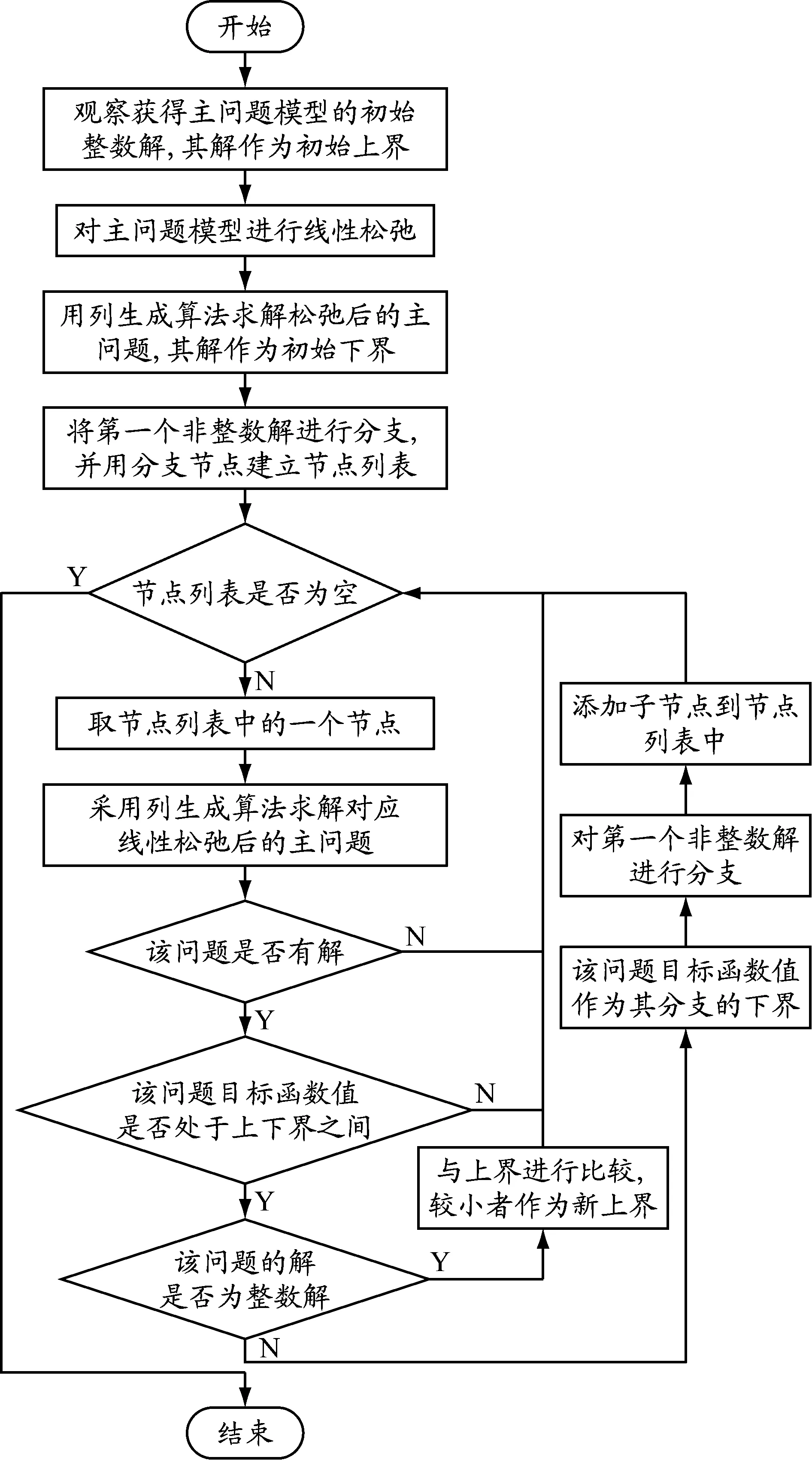
图1 分支定价算法设计流程

采用上述步骤可以获得最优的航次集合，但无法获得各航次的离港日期，即船期表。本文提出一种生成船期表的方法，该方法的具体流程见图2。

图2 船期表生成流程

2.2.2 模型分解

由于上述模型中含有大量的约束和变量，为求得模型的最优解，本文根据Dantzig-Wolfe分解原理，把上述模型分解成一个基于航行路径的主问题和一个含资源约束的最短路径子问题。

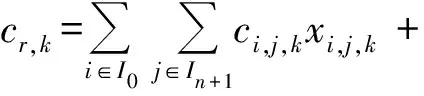
f,,≠；,,，若型供应船的航次访问海上设施，则为1，否则为0；,，若解中包含组合(,)，则为1，否则为0。主模型如下：

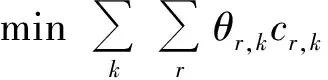
(19)

s.t.

(22)

式(20)和(21)与式(11)和(12)类似，式(22)表示变量约束。由于可行航次集中的组合(,)数量较多，本文采用列生成算法通过不断迭代为求解松弛后的主问题加入有效列(,)。

(2)子问题模型。表示海上设施到的距离；表示型供应船航行单位距离的可变成本；、分别代表式(20)和式(21)的对偶变量。主问题的检验数

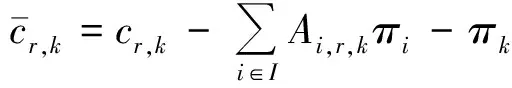
(23)

令+1=，则

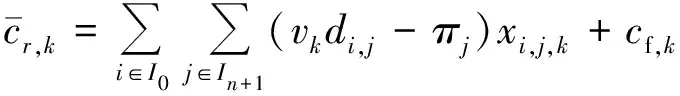
(24)

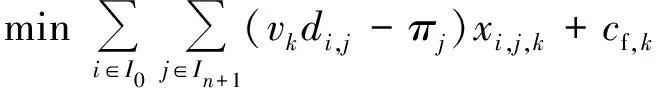
(25)

s.t.式(2)～(10)

式(25)表示在中寻找检验数小于零的组合(,)。子问题则为求解个独立问题，对于每一个问题所求得的目标函数值，只有小于零才能作为新的列代入主问题中进行迭代，以优化主问题的目标函数值；其中的定价是根据修改,,，得到新的可变成本,-，当不存在使得目标函数值小于零的列时，当前解即为松弛后主问题的最优解。

3 算例及分析

3.1 数据收集

由于部分数据较难获得，所以本文参照我国某石油服务公司的公开信息和HALVORSEN-WEARE等的相关数据，并根据实际情况进行设置。在备选船队方面，本文给出了6类船型(见表1)并提供了供应船甲板面积、经济航速等船舶信息。假定各类型船舶在规划期内的使用次数不超过3次，存在10个海上设施和1个陆上供应基地，且需要访问1次的海上设施为1、2、10，需要访问2次的海上设施为3、7、9，需要访问3次的海上设施为5、8，需要访问4次的海上设施为4、6。在渤海海域选取海上设施和陆上供应基地，图3为渤海海域海上设施和陆上供应基地的具体分布情况。

表1 供应船的主要参数

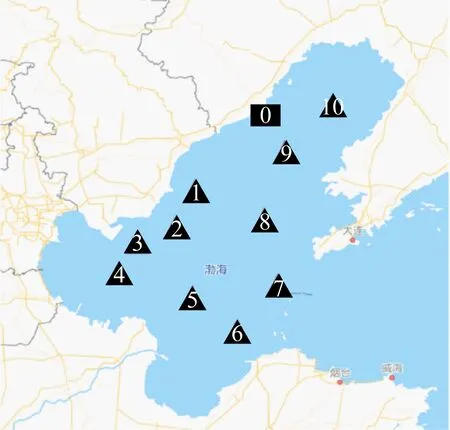
图3 渤海海域海上设施和陆上供应基地的分布情况

3.2 算例验证

本文程序的运行环境如下：计算机参数配置为AMD Ryzen 5 4600H with Radeon Graphics 3.00 GHz，应用MATLAB调用LPSolve工具箱编写计算程序。结合本文所提出的生成船期表的方法，得到表2所示算例优化结果。表2展示了在规划期内，根据各海上设施的需求及其所需的访问次数分别配置了相应的供应船、各船的航行路径、各航次的持续时间、各船的离港次数和离港日期等，并在可行的候选航次中选择了5个最优航次组合，使用了C、E两种船型。算例优化结果满足了规划期内各海上设施的访问次数需求、船舶容量约束、船舶使用次数约束，且每个航次的船舶装载量非常接近船舶容量，验证了本文模型及算法的有效性。

表2 算例优化结果

表3显示了在式(13)～(18)约束下，在规划期内需要进行多次访问的海上设施对应航次的离港日期分布比较均匀，验证了所提出的生成船期表的方法是可行的。

表3 供应船离港模式

3.3 敏感性分析

当船舶的固定成本(即定期租船成本)不变时，可变成本直接影响运营收益。因此，本文通过对可变成本进行敏感性分析，分析可变成本对船型选择的影响。在保证其他条件不变的情况下，将可变成本分别设为相对初始值逐渐增加0、50%、100%和150%，结果见图4。

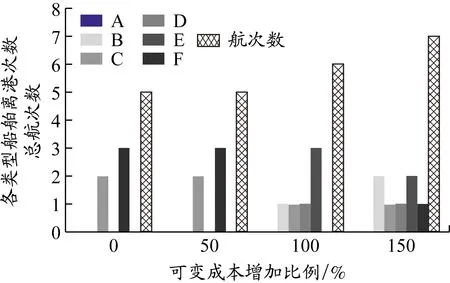
图4 各类型船舶离港次数及航次数变化趋势

由图4可以得出两点结论：(1)随着可变成本的增加，离港船舶的船型分布更加广泛；(2)当可变成本增加到一定程度时，总航次数呈现上升趋势，这是因为随着可变成本的增加，固定成本已经不是决定性因素。由可变成本敏感性分析可知，在进行船舶类型选择和航次规划时，供应船规划工作者应该考虑船舶使用期间可变成本的变化。

4 结 论

针对供应船规划问题(SVPP)，考虑在规划期内各海上设施需要访问的次数、供应基地和供应船容量约束、船舶均匀离港等因素，建立海上供应船调度与规划模型。运用分支定价算法求解模型并提出一种生成船期表的方法。以渤海海域为例进行算例验证，得到了规划期内的最优航次组合、每艘船的航行路径和离港次数、船期表，证明了算法和模型的合理性与有效性。通过对可变成本的敏感性分析可知：(1)随着可变成本的增加，离港船舶的船型分布更加广泛；(2)当可变成本增加到一定程度时，航次数呈现上升趋势。由此可知，在进行船舶类型选择和航次规划时，应该考虑船舶服役期间可变成本的变化。本文研究可以为供应船规划工作者提供更好的决策依据。