考虑服务优先级的绿色多式联运路径鲁棒优化
2022-09-30赵旭朱晓飞张瑶
赵旭,朱晓飞,张瑶
(大连海事大学交通运输工程学院,辽宁 大连 116026)
0 引 言
随着“一带一路”倡议的落实,多式联运成为一种能够有效实现物流设施的联通,保障贸易畅通,减少环境污染的重要运输组织形式。在货物运输多元化及经济全球化发展趋势下,多式联运服务质量也逐渐备受关注,若货物能安全准时到达,则满意度较高,若货物提前或延迟到达,则满意度会下降。因此,如何降低成本、提高满意度、实现交通运输绿色发展具有重要意义。
多式联运作为一个较为复杂的系统,可能由于内外部条件变化面临各种不确定性。此外,多式联运可能会受到随时加入的其他货物以及实际线路的限制,导致其不同运输线路的运输时间发生变化,从而使得其货物时间价值受到影响,因此有必要考虑货物时间价值服务优先级来处理各运输任务在运输中的相互影响。因此,本文研究的问题是一个考虑货物时间价值服务优先级的、带时间窗的、动态的绿色多式联运路径优化问题。
现有研究模型大多以成本最低、风险最低和时间最短等为目标。在绿色低碳背景下,碳排放因素通常体现在模型的目标或约束条件中,不同碳排放政策下多式联运路径选择结果通常不同。在不确定性分析方面,DEMIR等运用样本逼近方法优化时间和需求不确定时的绿色多式联运路径,WANG等运用期望值准则和临界值准则研究需求、成本和时间不确定时的多式联运路径。在优先级研究方面,李孟良等探讨了需求优先级约束下的应急物资多式联运调配策略问题,赵志文等研究了危险度优先级约束下的多类别危险品多式联运选址及路径规划问题,冯鹏等研究了到港船舶靠泊优先级和装船任务作业优先级约束下的煤炭出口码头装船作业调度优化问题。
当前关于多式联运路径优化的研究中考虑货物时间价值服务优先级的较少,且同时考虑碳排放、硫排放和混合不确定性(单位货物运费、运输速度、换装等待时间、运输线路可行概率的不确定性)的更少。基于此,本文引入货物时间价值服务优先级,在综合考虑不确定性、混合时间窗、运输能力、环境成本等的基础上建立鲁棒优化模型,使得总成本和托运人不满意度最低,最后通过分析不同情景得出较为理想的运输决策。
1 模型构建
1.1 问题描述与模型假设
多批货物需要在规定时间内通过包含公路、铁路、水路等3种运输方式的联合运输网络从起点运至终点。由于转运节点容量和运输线路容量有限,可能会发生运输延误或拥堵,从而导致货物时间价值损失和运输成本增加。基于此,本文根据货物时间价值优先原则,在运输任务到达中转节点后,依据其服务优先级在中转节点依次进行作业,若货运量不超过运输线路容量,则下一级任务可以继续选择上一级任务的运输线路,否则需重新进行选择。此外,实际网络可能存在诸多不确定性,如:装卸、运输操作不当造成货物损失;汇率变动、油价波动、疫情下货物供求情况和运营商主观因素等造成运费不确定;多变的交通状况和天气导致运输速度不确定;口岸通货能力不足、突发事故等导致换装等待时间不确定;自然灾害、设施破坏和公共卫生事件(如新冠疫情)等造成运输线路可行概率不确定。因此,本文研究在不确定性、时间限制、运输能力、环境成本等因素影响下,为不同服务优先级的任务确定总成本最低和托运人不满意度最低的最优路径问题。
为方便建模和求解,假设:(1)转运只在节点处且货流不可拆分;(2)仅铁路运输和班轮运输有发班时刻;(3)不补货或减货;(4)铁路运输与中欧班列运输的碳、硫排放相同,班轮运输在内河与远洋的碳、硫排放相同;(5)政府补贴不计入运费;(6)报关报检站与换装站为一点;(7)中欧班列仅在始发车站和边境站上货;(8)由于我国还未开征碳税、硫税,设碳税和硫税为固定值;(9)各不确定因素相互独立。
1.2 符号说明
集合。为运输节点集合,,,∈;为运输方式集合,,∈;为运输任务集合,∈。

变量。决策变量包括,,,、,,,。若在节点与之间任务采用运输方式,则,,,为1,否则为0。若在节点任务的运输方式由转换为,则,,,为1,否则为0。其他变量:若第次取值中节点与之间采用运输方式的线路可行,则,,,为1,否则为0。
1.3 多目标鲁棒优化模型构建

目标函数1为最小化所有情景下总成本的期望值:

(1)


g,),,,
(2)


(3)
=max{E,-d,,,0}+
max{d,,-L,,0}+
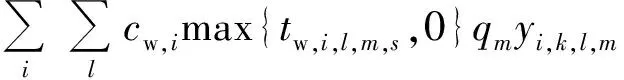
(4)
=v,(1-)
(5)
其中:为直接运输成本(运输成本和转运成本);为环境成本(碳排放成本、硫排放成本);为时间成本;为货物损失成本。
目标函数2为最小化所有情景下托运人不满意度的期望值:
min
(6)
=

(7)
s.t.

(8)

(9)

(10)

(11)

b,+g,+tg,),,,
(12)
w,,,,=

(13)

(14)
d,,≤L,
(15)

(16)

(17)

(18)

(19)
,,,-1=(+,,,),,,,-1>
(20)
,,,-1=(+,,,),,,,-1>
(21)
,,,,,,,,,,,∈{0,1}
(22)
式(8)表示两节点间最多选择一种运输方式;式(9)表示节点上最多进行一次中转;式(10)表示运输方式连续性;式(11)表示节点流量平衡;式(12)为换装完成时间;式(13)为等待时间;式(14)为到达节点的时间;式(15)为运输时间约束;式(16)~(18)表示单位运费、运输速度和换装等待时间取值满足鲁棒优化的最大保守程度;式(19)表示删除不可行的路线;式(20)表示上一级任务的运输剩余能力等于下一级任务货运量与其运输剩余能力之和;式(21)表示上一级任务的中转剩余能力等于下一级任务货运量与其中转剩余能力之和;式(22)为0-1变量。
2 模型求解
2.1 算法设计
本文模型是一个多目标整数规划模型,适合采用带精英策略的非支配排序遗传算法(elitist non-dominated sorting genetic algorithm,NSGA Ⅱ)进行求解,具体算法设计如下:
(1)编码与解码。染色体采用双层编码结构,第一层为运输路径编码,第二层为运输方式编码,如图1所示。解码时,运输路径终点之后的节点序列和运输方式中对应部分无效。

图1 染色体编码示意图
(2)初始化种群和快速非支配排序。首先随机生成父代种群,然后剔除运输节点间不存在通路或者不存在运输方式的个体。然后通过非支配排序对种群进行分级,对相同排序等级的染色体按拥挤距离进一步排序。
(3)选择、交叉和变异。采用锦标赛选择法进行选择操作:随机比较两个个体的排序等级,选择排序等级值小的个体进入子代种群,若两个个体排序等级相同,则选择拥挤距离大的个体进入子代种群。在交叉方式上,运输路径段采用顺序交叉可以避免子代染色体出现重复节点,运输方式段采用部分绘制交叉来保持种群个体的多样性,具体见图2。变异算子采用的是两点交换变异的方式,具体见图3。

图2 混合交叉示意图

图3 染色体变异示意图
(4)精英策略。将父代种群与其子代种群组合,有利于父代中的优良个体进入下一代,而且通过对种群中所有个体的分层存放,可以迅速提高种群水平。
2.2 多目标处理
决策者在决策时可根据实际网络情况、货物种类和托运人的实际需求对不同目标赋予不同的偏好权重,从而增加决策的灵活性,具体如下:
′=(-min)(max-min)
(23)
′=(-min)(max-min)
(24)
=′+′
(25)
式中:和分别为方案的任务总成本和不满意度;max和min分别为所有方案中任务总成本的最大值和最小值;max和min分别为所有方案中不满意度的最大值和最小值;和分别为任务总成本和不满意度的偏好权重;值越小代表决策越优。
3 案例分析
苏州水陆交通发达,在“一带一路”中作用重大。德国是中国在欧洲的最大贸易伙伴,中德贸易额约占中欧贸易总额的1/3。因此,本文选择苏州到汉堡的20个节点为研究对象。由于网络节点较多且我国与欧盟地区任意两个节点之间都有直达的公路和铁路,故部分直达路线没有画出。苏州与汉堡之间的多式联运网络见图4。

说明:R、T、W分别代表公路、铁路、水路运输方式
3.1 案例数据
运输距离数据源于交通运输部及全国公路、铁路和水路里程表。运输能力在区间内随机生成。铁路运输班期、中欧班列班期、水运班期参考中铁和中远集团相关数据。任务出发时间为2021年1月31日0时,运输集装箱为40英尺(1英尺=0.304 8 m)集装箱。参考中国海关网和文献[12],得到任务参数,见表1。参考文献[12-13],得到运输方式参数,见表2。公路运输平均速度与最高速度关系因子取0.75;铁路运输平均速度与最高速度关系因子,我国国内为0.7(因为我国路况较好且限速最高),欧盟段为0.6,独联体段为0.52(由于部分铁路如哈萨克斯坦段,老旧现象严重导致速度受限);内河平均速度与最高速度关系因子为0.6;远洋平均速度与最高速度关系因子为0.8。参考文献[6],得到运输方式转换参数,见表3。多式联运网络涉及的其他参数设置见表4。

表1 运输任务参数

表2 运输方式有关参数
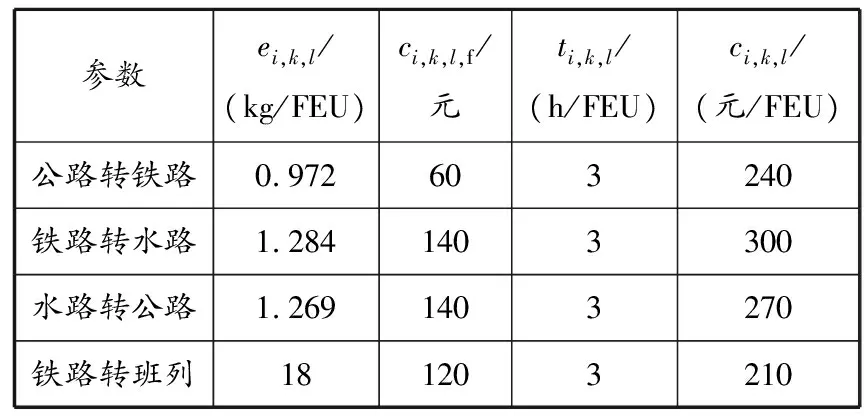
表3 运输方式转换参数

表4 多式联运网络涉及的其他参数设置
(1)公路基本运价为9元/(FEU·km),箱次费为25元/FEU,运价总体平稳,取10%。国内铁路运输基价1为436.3元/FEU,基价2为1.834 6元/(FEU·km);中欧班列运输基价1为680元/FEU,基价2为2.754元/(FEU·km),运输费率由满洲里出境为2.6元/(FEU·km),由二连浩特出境为2.5元/(FEU·km),由阿拉山口出境为4.4元/(FEU·km),欧盟段统一费率为6.5元/(FEU·km)。由于疫情影响,中欧班列运价飙升至疫情前的4倍,境外段取400%,其他铁路段取20%。水路集装箱运价参考市场运价,苏州至武汉为800元/FEU、武汉至重庆为1 000元/FEU,上海至汉堡为24 178元/FEU、深圳至汉堡为23 573元/FEU,水路运价较上月上升54.7%,取50%,和分别取-30%和300%。
(2)设置情景1~9来探究不同的单位运费、运输速度以及换装等待时间对路径优化结果的影响。从情景1到情景9,分别取0,0.4,0.6,0,0,0,0,0,0,分别取0,0,0,0.2,0.4,0.7,0,0,0,分别取0,0,0,0,0,0,0.1,0.3,0.6。设置情景10~12,选择任务1来分析不同的运输线路可行概率对路径优化结果的影响,分别取1、0.8和0.5。
3.2 求解结果
依据构建的鲁棒优化模型,设置=0.5,=0.5,=0.8,随机变量取值次数上限为100次。运用MATLAB R2018a求解模型,交叉概率取0.95,变异概率取0.2,种群数量取80,最大迭代次数取700。不同情景下的目标函数值的变化规律和优化结果见图5~10和表5。

图5 单位运费情景成本值

图6 运输速度情景成本值

图7 换装等待时间情景成本值
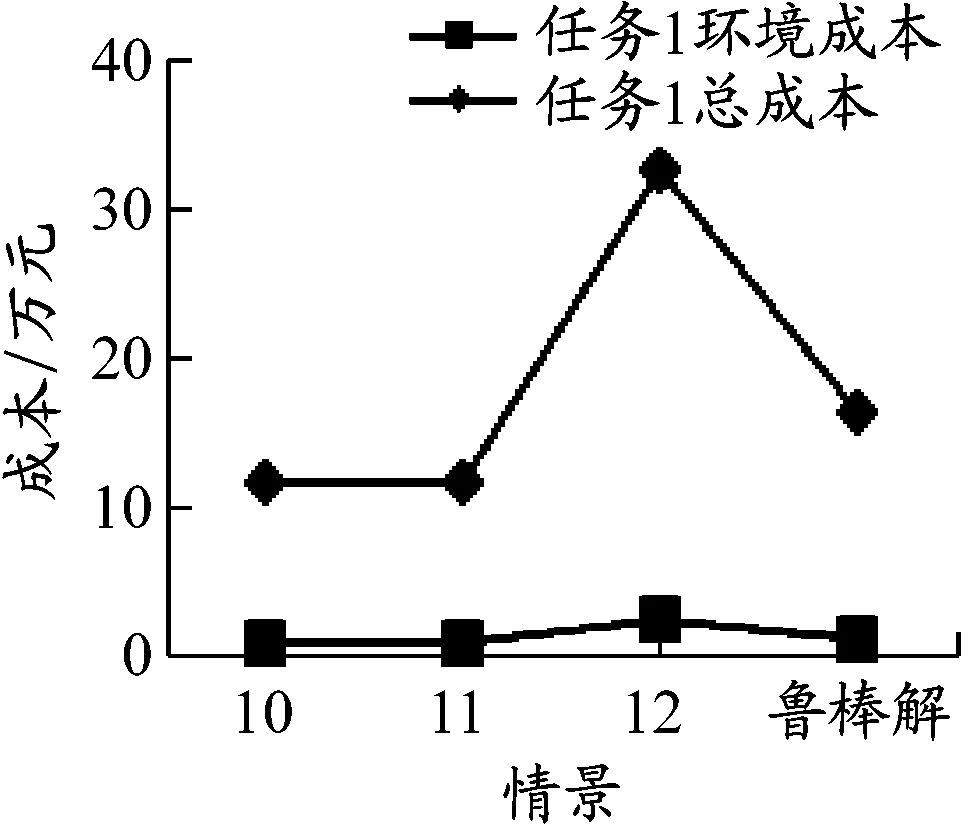
图8 线路可行概率情景成本值

图9 不同情景下托运人不满意度值

图10 不同情景下目标函数值

表5 多式联运路径优化结果
从图5~10可以看出,鲁棒优化结果较接近各不确定因素下情景2的优化结果。其结果表明,鲁棒优化能够提供较好的折中解。结合图5~10和表5可知:随着单位运费的增加,总成本都增加,运输决策均发生改变。随着速度的减小,对于时间敏感的任务,运输决策由铁水联运变为速度较快的公路运输或铁路运输,总成本较高,环境成本和不满意度较低;对于成本敏感的任务,多选择节点和弧段较少的单一铁路运输或公水联运,总成本较低,环境成本和不满意度较高。随着换装等待时间的增加,对于时间敏感的任务,运输决策由公铁水联运变为中转次数较少且环境成本较低的公路或铁路运输;对于以总成本最低为目标的任务,多选择节点和弧段较少且环境成本较低的铁路运输。随着线路可行概率的降低,总成本也相应增加。由此可见,多式联运经营人在决策时应综合考虑货物种类、托运人实际需求和实际网络情况,以获得更好的综合效益。
4 结 论
针对绿色多式联运路径优化问题,引入货物时间价值服务优先级,从运输总成本和托运人不满意度的角度,构建鲁棒优化模型,并采用带精英策略的非支配排序遗传算法(NSGA Ⅱ)进行求解,得到不同情景下较为理想的运输决策。结果表明:鲁棒优化可在参数概率分布未知的情况下提供较好的决策;不确定因素变化和决策者对不同目标的偏好均会影响运输决策的选择,对不满意度敏感的任务,其运输方式多为公铁联运,以总成本最低为目标的任务会使多式联运向更加经济的水路运输倾斜。本文研究可为绿色多式联运路径优化问题提供参考。
