相似三角形问题的解题策略研究

胡红伟 周凤霞

（1.湖北省十堰市茅箭区三堰小学 湖北十堰 442000;2.湖北省十堰市茅箭区致远学校 湖北十堰 442000）

绪论：有关三角形的存在性问题，中考常考查等腰三角形、直角三角形、相似三角形这三种，本篇重点讲解“相似三角形问题”的解题策略。相似三角形作为初中数学的重要组成部分，在历年的中考中已经越来越凸显其重要地位。相似三角形是全等三角形知识的延伸与拓展，作为中考的核心考点之一，它不仅考查学生对图形相似认识的深刻程度，更是对知识的综合应用提出了较高要求。

一、相似三角形证明与求解问题的分类梳理

1.对相似三角形的定义的辨析掌握

对应角相等、对应边成比例的两个三角形叫作相似三角形。平行于三角形一边的直线截其他两边所在的直线，截得的三角形与原三角形相似。相似三角形是初中数学学习的重点内容，对学生的能力培养与训练，有着重要的地位，而“相似三角形判定定理一”又是相似三角形这章内容的重点与难点所在，“难”的不是定理的本身，而是要跟以前学过的“角的等量关系”证明联系紧密，综合性比较强，因此对定理的运用也带来了障碍。“相似三角形判定定理一”应用的一个方面，这是根据对最近几年中考、各区县模拟考的压轴题的研究，发现全等三角形证明当中，我们可以找到“一条直线上有三个相等的角”这样的条件原型，所以，这节课就是基于这样的原型，选择了相关内容，试图从一个侧面突破的难点。

2.对相似三角形判定定理的运用

在对比中反复体验判定条件的运用，整理分析思路，积累解题格式和套路。这是以下判定方法证明的基础，也是不断梳理这类问题证明方法的分类积累。

常用的判定定理有以下6条，判定定理1至6：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。判定定理2：如果两个三角形的两组对应边成比例，并且对应的夹角相等，那么这两个三角形相似。判定定理3：如果两个三角形的三组对应边成比例，那么这两个三角形相似。判定定理4：两三角形三边对应平行，则两三角形相似。判定定理5：如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。判定定理6：如果两个三角形全等，那么这两个三角形相似。

学生所用的判定方法主要有以下5种：有平行截线：用平行线的性质，找“等角”；有一对等角：找“另一对等角”或“夹边对应成比例”；有两边对应成比例：找“夹角相等”或“第三边也对应成比例”或“有一对直角”；直角三角形：找“一对锐角相等”或“两直角边对应成比例”；等腰三角形：找“顶角相等”或“一对底角相等”或“底和腰对应成比例”。

3.需要改进的地方

相似三角形的判定教学内容还有待于进一步改进。教学的实践课要站在更高的角度来思考，反映出我们要不断归纳，应该把类题型至少要细分为基本图形的形成、基本图形的巩固、基本图形的拓展应用三个层次，相似三角形判定的引例、判定定理（1）的内容在探究方法上又具有一定的相似性，因此教学安排上注意方法上的新旧联系，以帮助学生形成认知上的正迁移。此外，由于判定定理2的条件相应的夹角相等在应用中容易让学生忽视，所以教学设计采用了小组讨论加集中展示反例的学习形式来加深学生的印象，在具体引导学生接受过程中，要力求使探究途径多元化，把学生利用作图工具作静态探究与应用。

让学生充分感受探究的全面性，丰富探究的内涵，协同式小组合作学习的开展不仅提高对三角形判定的定理的反复运用。对比条件核查与已知条件相适应的判定模式，直到证明或求解模式构建成功，分析解题套路打通，形成经验积累中相对固定的解题建构模型。

4.从学生的认知规律中梳理相似三角形的判定问题

学生在体验了“实验操作——探索发现——科学论证”的学习过程后，从单纯地重视知识点的记忆、复习变为有意识关注学习方法的掌握、数学思想的领悟。学生在探究矩形的比值时，就能意识地把解决特殊问题的策略、方法迁移到解决一般问题中去，而且还能感悟一题多解、一题多变等数学学习方法。

相似三角形的判定主要介绍了三种方法以及相似三角形的预备定理，从结果来看，不是很理想，绝大部分学生对定理的应用不是很熟练，特别对于“两边对应成比例且夹角相等”不能灵活运用，夹角也不能准确找到。我想问题的主要原因在于学生对图形的认知不深，对定理的理解不透，一味死记结论，不能理解每个量所表示的含义。我想在现阶段应培养学生认识图形的能力、合情推理的能力，争取这方面有所提高。

教师是学生学习的组织者、引导者、合作者、共同研究者，鼓励学生大胆探索，引导学生关注过程，及时肯定学生的表现，鼓励创新，哪怕是微小的进步都给予热情赞扬。教师只在关键处点拨，在不足时补充。

二、解题思路架构分析和探索解题方法归纳

1.结合已知条件，恰当引入参数，巧妙构造相似。

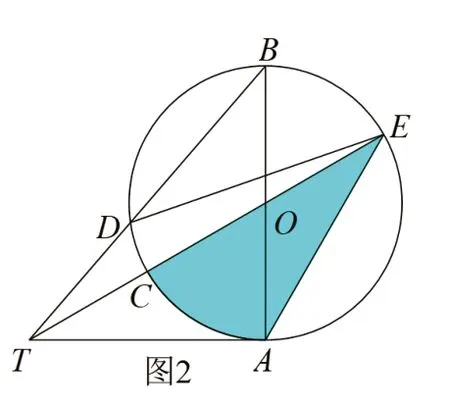
例：如图1，AB为⊙O的直径，TA为⊙O切线，BT交于⊙O点D，TO交⊙O于点C，E.（1）若BD＝TD，求证：AB＝AT；（2）在（1）的条件下，求tan∠BDE的值；（3）如图2，若BD/TD＝4/3，且⊙O的半径r＝，则图中阴影部分的面积是__________。

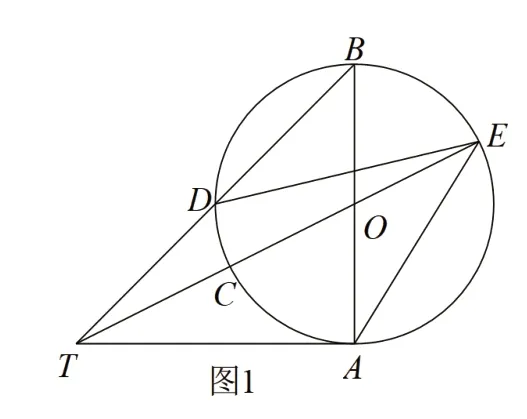
解题对策的研究：针对问题先进行思路分析，初步形成解题框架，较快找到突破口。要牢记求解目标，要求tan∠BDE的值，一般要把所求角放在直角三角形中。其主要方法是要么作垂线直接构造直角三角形，要么把∠BDE转化为已在某个直角三角形中的角。这里很容易想到连接BE，根据AB为直径，以及同弧所对的圆周角相等，由∠BDE=∠BAE，从而在直角△ABE中考虑∠BAE的正切值即可。但此时BE与AE的数量关系并不明确，tan∠BAE的值仍然无法求得。若此时过点E作AB的垂线EH，把∠BAE放在直角△AEH中考虑就迎刃而解了。此时，借助（1）中的结论AB=AT，通过构造△OEH与△OTA相似，再借助半径OA=OE的相等关系，通过设OH=m，引入参数，进一步明确△AEH中三边的数量关系即可求出tan∠BAE的值，也就是tan∠BDE的值。

不规则阴影部分面积必须要对其合理切割。这里可以切割成扇形OAC和△OAE.对于扇形，在半径已知的情形下，欲求面积则必须先解决弧长或圆心角的度数，别无他法。连接AD，结合已知条件引入参数，可设BD=4a，TD=3a，再借助三角形相似（或射影定理）和勾股定理得到a=1，从而求得，由边的关系进一步可以得到∠AOC=60度，只要突破了∠AOC的度数这一关键性结论，扇形AOC和△AOE的面积均可得到妥善解决。

2.垂径定理与勾股定理巧融合，借助二次相似达成目标

如图1，△ABC内接于⊙O，∠BAC的平分线交⊙O于 点D，交BC于 点E（BE＞EC），且BD=.过 点D作DF∥BC，交AB的延长线于点F.（1）求证：DF为⊙O的切线；（2）若∠BAC=60°，，求图中阴影部分的面积；

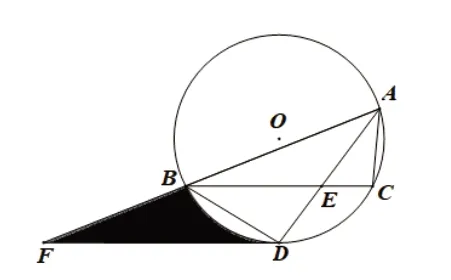
图1

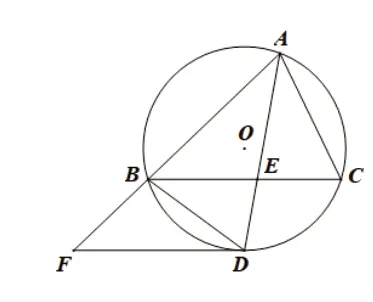
图2

问题的分析：对于问题（1）的分析，属于典型的“连半径、证垂直”类问题，连接OD与BC交于点N，学生易于入手。对问题（2）的分析，要用好60度特殊角，运用垂径定理和勾股定理，分别得到BN、NE、ND和CE的值；再由△BDE和△ACE相似，求出AE和AD的值；最后再根据△ABE与△AFD相似得到DF的长。求出DF后，所求阴影部分面积就可以看成是△BDF与其所含的弓形面积之差，从而使问题最终解决。

解题对策的研究：最后问题的解决依赖于两个已知条件的正确使用，它仍然属于二次相似的典型应用。这里线段数量关系比较复杂，需要通过引入参数来把几条线段的关系“串起来”。例如，可设所求的线段BF=x，首先通过△FDB与△FAD相似来准确表示出AB与AC，再根据△ACD与△DBF相似来确定未知数x的值即可。

3.应用二次相似进行比值转换。

例：（2017年十堰市中考题）已知，AB为半圆O的直径，BC⊥AB于点B，且BC=AB，D为半圆上一点，连接BD并延长交半圆O的切线AE于点E.

（1）如图1，若CD=CB，求证：CD为半圆O的切线；

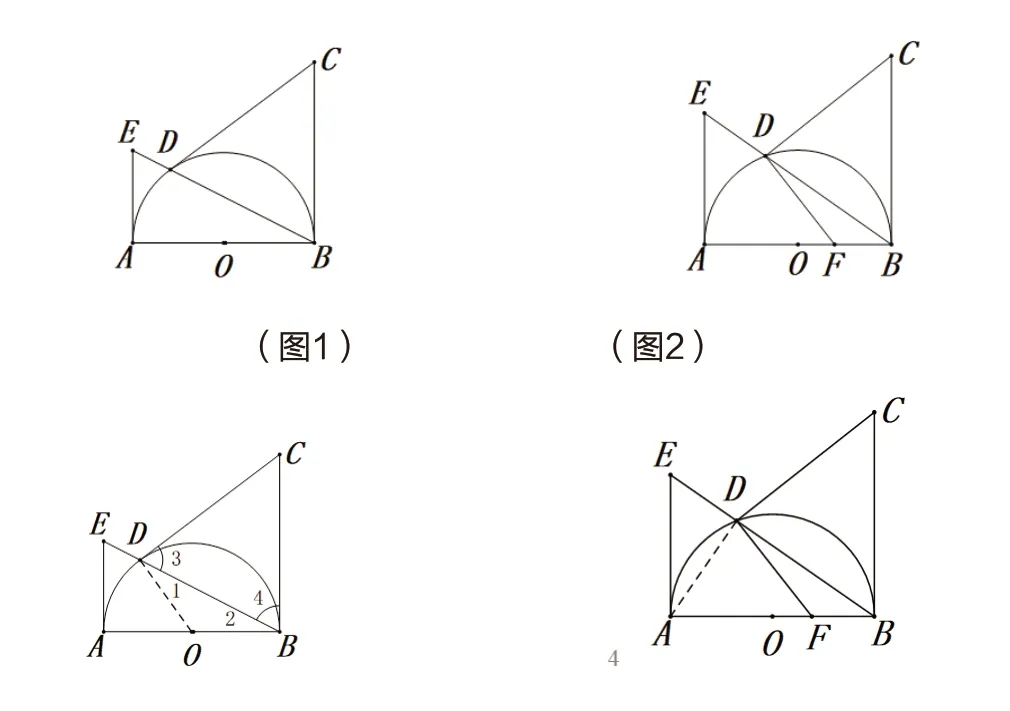
问题的分析：问题（1）仍然属于“连半径、证垂直”。通过连接半径OD，借助“等边对等角”和BC⊥AB这一已知条件，来得到∠ODC为直角，进而说明CD为半圆O的切线。

问题（2）中连接AD，结合AB是圆O的直径得到∠ADB=∠ADE=90°，从而△ADE∽△BDA

解题对策的研究：这道题在已知条件中并没有给出任何一条线段的值，而最后的结论却要求两条线段的比值，这也说明我们必须要弄清与AE和AF相关联线段之间的密切联系。分别把AE和AF放在各自所在的三角形中进行考虑，从这个角度出发，连接AD就显得必然了；另一方面，△ADE为一直角三角形，而△AFD却是一锐角三角形，通过观察图形结构再分别研究与这两个三角形相似的特征三角形，以线段AE和AF为目标线段，写出相关的对应比值，抓住AB=BC这一关键性条件，正确的解题思路就形成了。

结语

综上所述，相似三角形的问题现阶段已经成为中考必考的热门考点之一，特别是对于二次相似的应用，其解题要求较高难度较大的特点已越来越受到广大师生的重视。它需要我们在教学中去不断地总结经验、提炼方法，灵活应用题目条件中的边角关系，合理构造相似三角形。相信通过同学们的辛勤努力和广大教师的高效引领，越来越多的学生能够成功跨越“二次相似”这一难关。