深地热开采热能提取效率研究及对EGS-E的启示

李迎春，孙文明，亢方超，唐春安

1) 大连理工大学深地工程研究中心，大连 116024 2) 广东石油化工学院机电工程学院，茂名 52500

深地热资源因其储量丰富、绿色清洁、稳定可持续等优点而受到广泛关注[1]. 传统的深地热开发系统一般通过地面钻井至干热岩储层，然后利用水力压裂技术改造储层，增强储层的渗透性，从注入井注入换热工质（一般为水）流经干热岩储层吸收热量，最后通过生产井提升至地表进行利用. 此深地热开发系统主要依靠钻井施工至热储水平，因此可称为EGS-D (Enhanced geothermal system based on drilling)[2-3]. 从1973年在美国Fenton Hill测试的首个EGS-D项目以来，近50年来在全球范围内约42个EGS-D项目，但这些项目大多难以维持商业化运转[4]. 通过梳理这些项目未能成功商业化的原因主要有以下几点：（1）热储规模不足，水力压裂效果不明显，如美国的Fenton Hill项目；（2）换热工质流动范围不可控，流体大规模流失，如英国的Rosemanowes和日本的Ogachi项目；（3）水力压裂诱发地震，如瑞士的St Gallen和韩国的Pohang项目[5-13].

为克服EGS-D的不足，近年来大连理工大学深地工程研究中心提出了基于成熟地下采矿技术的深地热开发系统，即EGS-E (Enhanced geothermal system based on excavation). 此系统主要是通过开挖竖井至干热岩热储的设计开采水平，然后通过大巷、经准备巷道至矿体（热储）；热储可通过爆破或水力压裂等方法进行自然崩落，崩落后的干热岩块体运至中央换热池进行热交换，从而实现大规模热储定制，控制热储垮落范围、约束热储与换热工质的热交换过程[14-15]. 另一方面由于EGSE的整体技术框架与地下采矿技术一致，因此较易实现矿热共采，即在浅部低温区进行常规矿产资源开采，中部中温区先采热降温后采矿，高温区完全采热[16-17]. 对于中温区的矿热共采工艺流程，可通过爆破或水力压裂工艺分层致裂热储，制造贯穿或随机裂隙，注入换热工质，进行第一次换热，同时起到取热和降温作用. 预裂降温后的热储通过自然崩落法进行大规模崩落破碎，运至中央换热池，进行二次换热.

不管是传统的EGS-D还是新提出的EGS-E，最终目的均是利用换热工质提取热储中的热量；而热储换热效率和采热量很大程度上取决于热储改造模式和相应的换热方式. 纵观地热开发系统，改造后的热储可简化为以下四个模型：高渗透率热储模型（对应EGS-E中崩落后的破碎块体）、贯穿裂隙热储（对应管道换热系统）[18-23]、随机裂隙热储模型（对应EGS-D中水力压力技术改造后的热储）[24-26]、以及贯穿裂隙+随机裂隙热储（复合换热系统）. 由于从实验层面很难实现4种热储模式换热效率和采热量的直接对比，因此本文通过COMSOL Multiphysics多场耦合软件系统研究了热储改造方式对热能提取效率和采热量的影响，为EGSE采热方式的选择和优化提供有效指导.

1 基本假设和控制方程

1.1 基本假设

为了方便数值计算，对裂隙开度演化数值模型做如下假设[27]：

(1) 岩体的物理力学性质均匀、各向同性；

(2) 初始状态下，岩体中的温度分布均匀且为同一数值；

(3) 岩体中没有热量的产生和散失，热量由岩体垂直传导到裂隙中的流体.

1.2 控制方程

我们在COMSOL Multiphysics中耦合了裂隙流、固体力学、固体和流体传热等模块，固体和流体之间的热导率随温度的变化而改变[28]，各模块的控制方程如下：

裂隙中的流体流动遵从质量连续性：

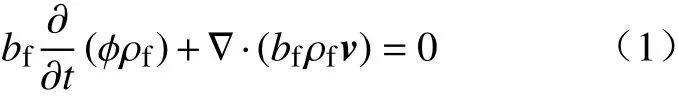
其中，bf为 裂隙开度，m；t为注入时间，s；φ为裂隙孔隙度；ρf为 流体密度，kg·m-3；v为达西速度矢量，m·s-1；可以表示为：

其中，µ是流体动力黏度，Pa·s；p是裂隙内的流体压力，MPa；K是依据立方定律计算的裂隙渗透率，mD：

联合公式(1)、(2)和(3)，可以得到裂隙中流体流动的控制方程：

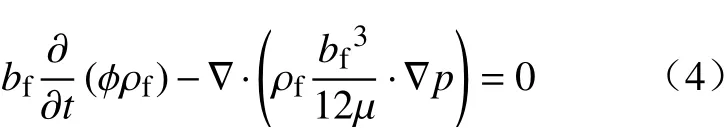
裂隙传热基于对流扩散方程：

其中，cf为恒定压力下的流体的比热容，J·kg-1·K-1；Tf为流体温度，℃；kf为流体的导热系数，W·m-1·K-1.

基岩传导传热基于傅立叶定律的微分形式：

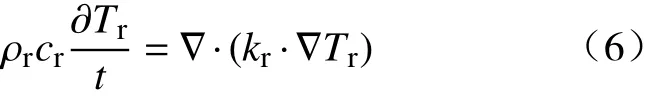
其中，ρr为 岩体密度，kg·m-3；cr为恒定压力下的岩体的比热容，J·kg-1·K-1；Tr为 岩体温度，℃；kr为岩体的导热系数，W·m-1·K-1.

基岩降温过程中产生温度应力和流体压力共同作用于模型的下边界. 考虑热弹性和流体压力（压应力为正值）的本构方程为：

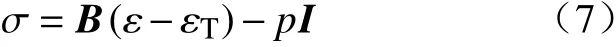
其中，B为弹性矩阵；I为特征矩阵；εT为温度应变，可以表示为：

其中，α为热膨胀系数，K-1；Tini为岩石初始温度，℃.

裂隙开度是法向应力的线性函数：

其中，sn为 裂隙的法向刚度，MPa；Δσn为裂隙的法向方向的应力变化值，MPa.

2 热储改造方式对热能提取效率的影响

2.1 数值模型

图1(a)展示了在COMSOL Multiphysics软件中构建的热储换热几何模型. 模型长度和宽度分别为1000 m和400 m，热储面积为4.0×105m2. 换热流体（水）以恒定的质量流量（Qf）从左边界（AB）注入，右边界（CD）流出；模型上边界（BC）和下边界（AD）为恒温边界，温度为200 ℃，左边界（AB）和右边界（CD）为热绝缘；模型全部边界（AB、CD、AD和BC）的力学条件均为辊约束. 在开展热储改造方式对热能提取效率数值模拟时，模型的基岩以及换热工质的物理和力学参数如表1所示.

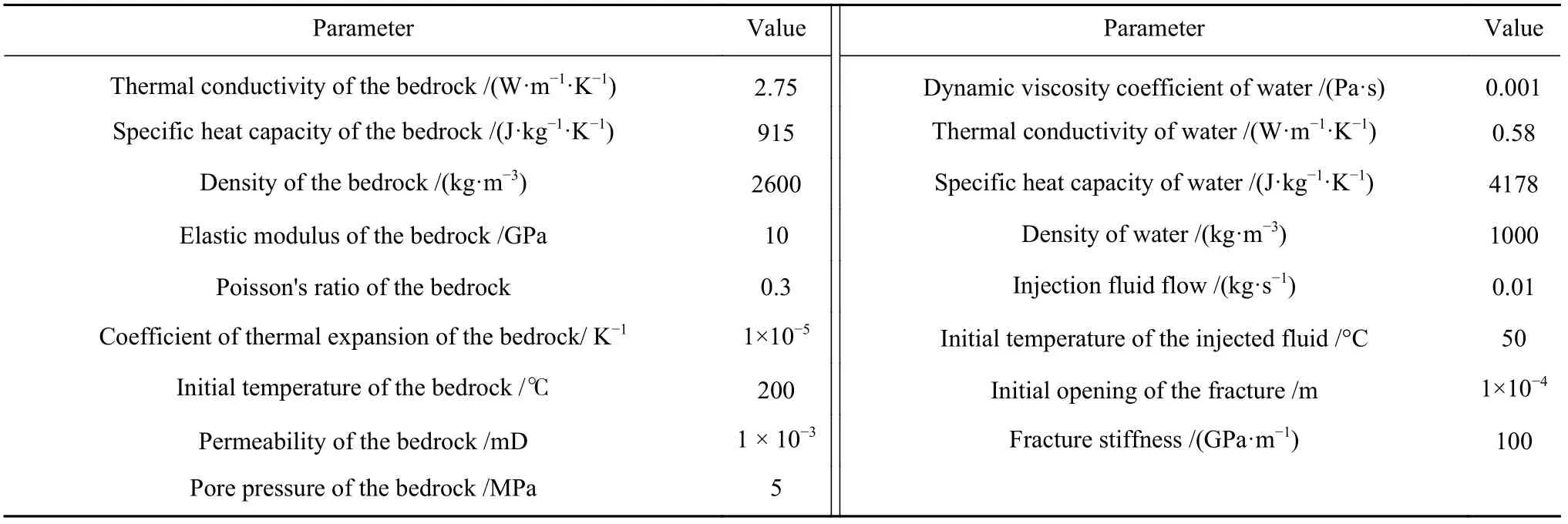
表1 热能提取效率研究数值模型中的物理和力学参数Table 1 Physical and mechanical parameters used in the numerical model

为研究不同热储改造方式对热能提取效率的影响，本文对比了以下4种热储改造方式：

(1) 高渗透率模型（图1(b)）：将基岩渗透率从1×10-3mD提升至1×103mD，研究高渗透率热储的热能提取效率. 此模型可代表EGS-E中充分垮落的干热岩与换热流体的换热.

(2) 贯通裂隙（或管道）模型（图1(c)）：在热储基岩中等间距布置3条贯通裂隙（或管道），研究仅使用贯通裂隙（或管道）进行热储改造时的热能提取效率. 贯穿裂隙模型中水流可以流动至周围岩体，而管道模型中不可以.

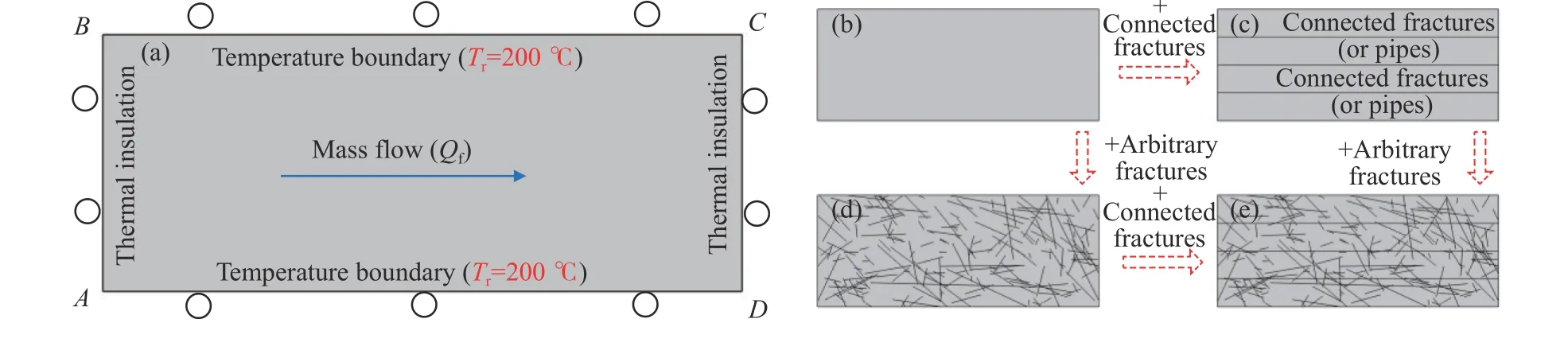
图1 数值模型. (a) 热能提取效率研究数值模型; (b) 高渗透率模型; (c) 贯通裂隙（或管道）模型; (d) 随机裂隙模型; (e) 贯通裂隙+随机裂隙模型Fig.1 Numerical model: (a) numerical model for heat extraction efficiency study; (b) high permeability matrix model; (c) connected fracture (pipes)model; (d) random fracture model; (e) connected fracture and random fracture model

(3) 随机裂隙网络模型（图1(d)）：在热储基岩中增加定量的随机裂隙（随机裂隙参数如表2所示），模拟采用爆破崩落或水力压裂等技术改造后的热储状态，研究随机裂隙热储的热能提取效率.

表2 随机裂隙属性Table 2 Random fracture properties

(4) 贯通裂隙+随机裂隙模型（图1(e)）：在热储岩体中同时增加随机裂隙和贯通裂隙，模拟热储分层改造后的裂隙分布状态，研究分层改造热储的热能提取效率.

2.2 不同改造模型温度场演化规律

图2展示了四种热储改造模型的温度场演化规律. 高渗透率热储的冷锋最早出现在注入边界，并均匀布满整条边界（图2(a)）. 随着注入时间的增加，冷锋沿着流体注入方向不断推进，热储降温区域逐渐增大并沿流体注入方向呈现出明显的温度梯度. 由于模型上下边界为恒温，冷锋在垂直方向的影响区域逐渐缩小，但幅度较小. 进一步增加注入时间导致冷锋的影响范围进一步增大，沿注入方向的温度梯度更加明显. 当注入时间（t）达到30 a时，冷锋已接近热储流出边界.

图2 温度场演化规律. (a)高渗透率热储温度场演化规律; (b) 贯通裂隙（管道）热储温度场演化规律; (c) 随机裂隙热储温度场演化规律; (d) 贯通裂隙+随机裂隙热储温度场演化规律Fig.2 Temperature field evolution: (a) high-permeability reservoir model; (b) connected fracture (or pipes) model; (c) random fracture model; (d) connected fracture and random fracture model

随机裂隙热储的冷锋最早出现在注入边界（图2(c)），这与高渗透热储有一定的相似性，但其传播方式却显著不同. 由于裂隙的渗透率远高于基岩，注入流体优先沿裂隙流动，导致随机裂隙热储的冷锋总是出现在裂隙区域. 而且裂隙密度越大，连通程度越高，冷锋出现的时间越早，影响范围越大. 注入时间为5 a时，冷锋在热储区域内的影响范围基本相同；当注入时间增加到10 a时，由于热储下部的裂隙密度比热储上部更高，且连通性更好，流体优先流向热储下部，冷锋的影响范围也更多的出现在下部区域. 这种差异性随着注入时间的增加而愈发显著，当注入时间增加到30 a时，热储下部区域的降温程度要远高于热储上部. 贯通裂隙热储的冷锋最早出现在贯通裂隙（图2(b)）.随着注入时间的增加，冷锋的影响范围沿裂隙平行方向逐渐扩大. 同时，冷锋的影响范围在流体的注入端最大，沿着注入方向不断减小. 由于热储上下边界为恒温，始终有热量沿边界流入热储，所以裂隙与上下边界之间的区域降温幅度明显低于裂隙间的区域，而且这种差异性随着注入时间的增加逐渐增强. 随机裂隙+贯通裂隙热储的冷锋最早出现在贯通裂隙周围（图2(d)），类似于贯通裂隙热储. 随着注入时间的增加，冷锋首先沿贯通裂隙平行方向扩展，之后逐渐出现在与贯通裂隙相联通的随机裂隙附近. 此外，贯通裂隙和与之相连的随机裂隙逐渐将热储切割成许多独立的区域，该区域内基岩温度降低幅度普遍大于未被切割的区域；未与贯通裂隙连接的区域冷锋出现的时间较晚，降温幅度也较小.

以上结果表明4种热储改造方式中，高渗透率热储的降温幅度最大，其次是随机裂隙热储，随后是随机裂隙+贯通裂隙热储，最小的是贯通裂隙（管道）热储，这表明在相同的注入时间内，高渗透热储的热能提取效率最好.

2.3 不同热储改造方式的年采热量

地热系统的采热量与基岩的孔隙度、基岩密度、基岩比热容、流体密度、流体比内能等因素密切相关，可根据式（10）进行计算[29-30]：

其中，Q代表采热量，GJ；φ代表孔隙度；ρr代表基岩的密度，kg·m-3；cr代表基岩的比热容，J·kg-1·K-1；Tr代表初始温度，℃；ρf代表液体的密度，kg·m-3；uf代表液体的比内能，J·kg-1.

图2对比了不同改造方式热储温度场的演化规律. 模拟结果表明随着注入时间的增加，不同改造方式的热储流体冷锋影响范围和热储降温区域均逐渐增加，但其降温路径存在显著差异. 第一组模拟比较了不同换热方式（高渗透率基岩、随机缝网、随机缝网+贯通裂缝、贯通裂缝、管道）的热采出率，如图3(a)所示. 这组模拟基岩初始温度为200 ℃，换热流体注入温度为20 ℃，结果表明这5种模型的年采热量在30 a内均能保持在1400 GJ以上. 对比图3(a)中5条曲线可以发现，均匀的高渗透率基岩可以得到最多的年采热量，且在连续采热15 a后，高渗透率基岩年采热量为贯通裂缝和管道采热量的2倍. 高渗透率基岩和随机缝网的年采热量在前7年基本重合. 但高渗透率基岩的年采热量在30 a内保持在4000 GJ以上，比较平稳，随时间增加只有较小幅度降低. 随机缝网的采热量从第7年开始有明显降低，但仍然远远高于其他三种换热方式. 模拟得到的随机缝网+贯通裂隙、贯通裂隙和管道3种换热方式的年采热量变化趋势大致相同，基本上呈现负指数函数衰减. 如图2(b)和图2(c)所示，由于贯通裂隙是热储内的优势流体通道，液体会优先沿该通道流动，造成液体流速较快，周围基岩温度下降较快，裂隙开度会迅速改变；而随机裂隙为非贯通裂隙，液体流速较慢，周围基岩降温较为缓慢，裂隙开度改变速度相对比较慢. 这就导致了图3(a)所示结果，在地热开采初期，贯通裂隙的年采热量较大，但是优势通道会削弱流体向热储渗透的能力，随着开采时间的增加，贯通裂隙的年采热量迅速降低，而随机裂隙的年采热量降低较为缓慢，在经过2～3 a的开采时间之后，随机裂隙的年开采量逐渐超过贯通裂隙.

根据以上结果可知，制造大量次生裂隙来均匀增强基岩的渗透率，对提高采热量和保持稳定的采热量最有利. 针对EGS-E，垮落区和换热池采用裂隙流换热优于管道流换热. 同时，在垮落区制造均匀分布的密集缝网（如高渗透率模型）可以提高采热量，避免采热量随时间快速衰减.

2.4 不同流体注入温度的热能提取效率

第二组模拟比较了不同的注水温度（20、40、60、80和100 ℃）对采热量的影响. 假设基岩平均渗透率为1×104mD，初始温度为200 ℃. 模拟结果及对应曲线拟合如图3(b)所示，其中Tin代表注入流体的温度. 结果表明，注水温度越低，年采热量越大. 注水温度越低，出口水温越低；但注水温度越高，出口水温随时间变化越小，越容易保持水温恒定. 同时，随着注入时间的增加，热储的热能提

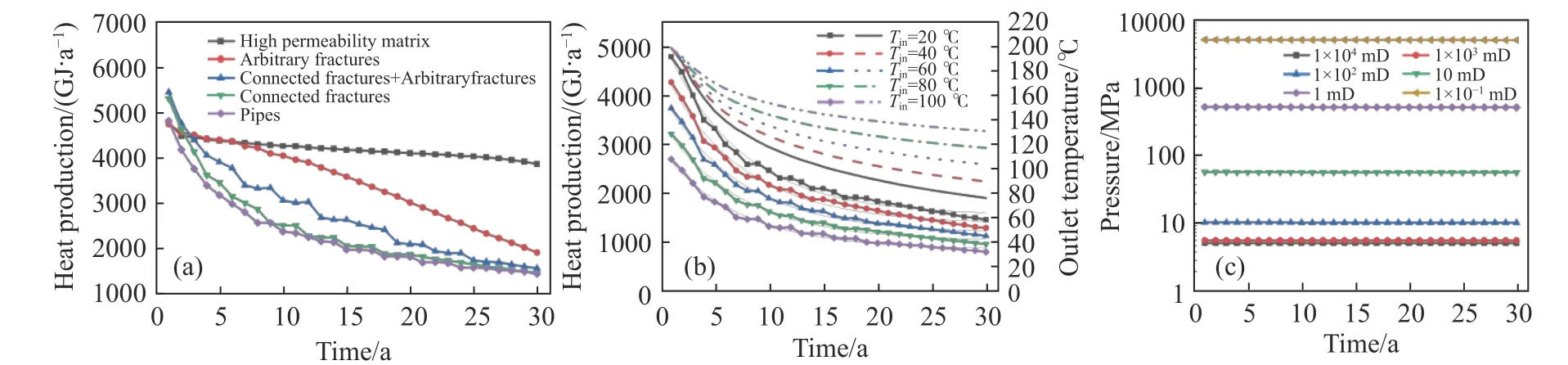
图3 不同换热方式的热能提取效率. (a) 不同换热方式年采热量对比; (b) 不同注水温度的年采热量和出水温度对比 (散点折线图为采热量、折线图为出水温度、细线为拟合曲线); (c) 不同基质渗透率入水压力比较Fig.3 Performance of different heat extraction approaches: (a) comparison of annual heat production using different heat exchange models; (b) comparison of annual heat production and water outlet temperature at different water injection temperatures (the scatter-line graph is the amount of heat production; the broken-line graph is the water outlet temperature; and the thin-line is the fitting curve); (c) comparison of water inlet pressure at different matrix permeabilities

取效率呈负指数函数迅速降低，注入时间与热能提取效率的相互关系如表3所示，其中y为热能提取效率，t为注入时间，a、b和c为常数变量.

表3 不同注水温度的采热量曲线拟合Table 3 Curve fitting of heat recovery at different water injection temperatures

不同注水温度的年采热量曲线拟合参数如表3所示. 对比发现5条拟合曲线的系数c基本相等，说明不同注水温度的年采热量曲线变化趋势基本一致，曲线之间数值呈倍数关系，注水温度为100 ℃的模型采热量约为注水温度为20 ℃的模型采热量的56%. 若EGS-E模型的换热池向垮落区提供100 ℃的注水温度，在30 a内可保证换热池回流温度稳定保持在140 ℃以上.

第三组模拟比较了不同的基岩渗透率（1×10-1mD～1×104mD）30 a采热量. 在模拟中不考虑由于注水导致的岩石破裂，假设基岩初始孔隙水压力为5 MPa，模拟结果如图3(c)所示. 通过图中6条曲线可以看出，基岩渗透率越低需要的注水压力越高，说明需要更多的能量来提高水压. 为保证基岩的稳定性和较高的采热效率，针对EGS-E，建议改造后的垮落区平均渗透率大于100 mD.

3 裂隙开度演化规律

EGS-E矿热共采的另一个问题是如何设置爆破/压裂参数对热储分层致裂[31]，进行第一次取热降温. 为此，本文建立了一个多平行裂缝的地热系统模型来研究热力作用和水力作用对储热渗透性改造的长期效果，以及裂缝间距（岩体尺寸）对裂隙开度演化规律的影响.

3.1 数值模型

图4(a)是一个多平行裂缝的EGS-E分层取热降温的示意图，具有多组由水力压裂产生的均匀分布的平行裂缝. 考虑到模型内流体流动和储层性质的均匀性，将计算域简化为一个嵌在两个岩体块中的裂缝. 同时由于模型的对称性，该计算域可进一步简化为半边岩体和半边裂缝. 在开展裂隙开度演化规律数值模拟时，模型的基岩以及换热工质的物理和力学参数如表4所示. 在简化的模型中，通过在裂缝的左侧注入给定速率的水，保持其恒定质量流量为2Qf，并在其右侧保持恒定压力来实现流动循环. 流体循环不仅可以在裂缝表面上施加压力，还能够从岩体中提取热量，导致岩石冷却收缩，而裂缝表面的水压和冷却引起的岩石收缩均可以增加裂缝开度. 该模型模拟深部环境下的低渗透性岩石，因此可以忽略岩石中的多孔流动和从裂缝向岩体的渗流. 模型边界的力学边界均为辊约束.

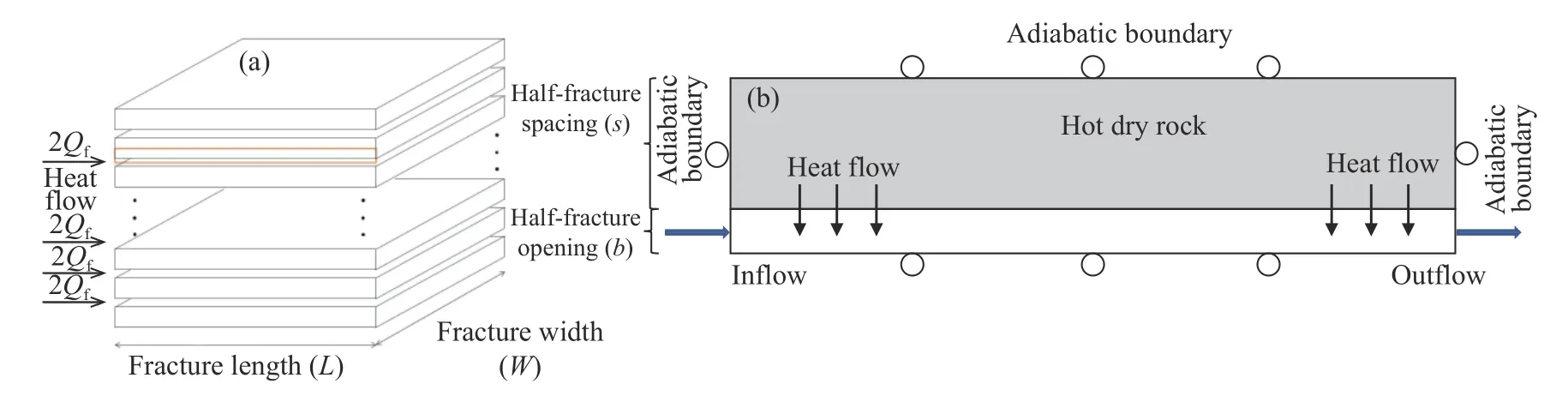
图4 取热示意图. (a) 分层取热EGS-E图; (b) 分层取热EGS-E数值模型图Fig.4 Schematic diagram of heat extraction: (a) illustration of EGS-E with multiple slices and (b) numerical model of EGS with multiple slices

表4 裂隙开度演化数值模型中的物理和力学参数Table 4 Physical and mechanical parameters used in the numerical model

3.2 热力作用对裂缝开度的影响

为揭示热力作用对裂缝开度的影响，本文分别模拟了HM（等温注入，流-固耦合）和THM（非等温注入，热-流-固耦合）两种情况，模拟结果如图5(a)所示. HM的模拟结果（蓝色曲线）表明，注入井附近的裂缝开度在很短时间内即可达到稳定状态，最大值为2.37×10-4m. 而THM的模拟结果（红色曲线）则完全不同. 由于热力作用的影响，注入井附近的孔隙开度随着时间的增加而增大，其数值从0.1 a时的2.5×10-4m增加到10 a时的2.84×10-4m，而且这种增大趋势还沿着生产井方向逐渐传播. 因此，与HM模型相比，THM模型中注入井周围具有更大的裂缝开度.

图5(b)和图5(c)分别分析了HM和THM情况下水力作用和热力作用对裂缝开度影响. 在HM情况下，裂缝开度的增大仅受水压分布的影响，如图5(b)中蓝色曲线所示；而对于THM情况，水压变化引起的裂缝开度变化则随注入时间的增大而减小，如图5(b)中红色曲线所示. 产生这种现象的原因是由于低温流体注入后，导致高温岩体产生了热收缩，从而造成裂缝开度的增大（图5(c)）.因此，在恒定的流体质量的前提下，水流压力随着裂缝开度的增大而逐渐减小，随之而来的是注水量的逐渐增加. 如图5(d)所示，在注入开始时，注水 量 的 断 崖 式 跌 落（从0.086 kg·s-1·MPa-1降 至0.076 kg·s-1·MPa-1）是因为，当流体注入裂隙后，使得压力开度在短时间内急剧上升至最高值，而此时基岩降温幅度小，累积的冷却收缩也不明显，裂隙内的流体压力迅速提高并达到稳定，导致流体注入量急剧减小. 随着注入时间的增加，流体冷锋逐渐向基岩内部扩展，基岩降温区域增加，温度的降低导致基岩冷却收缩逐渐增强，冷却开度也随之增加，在相同的质量流量下，裂隙内的流体压力随着冷却开度的增加而逐渐降低. 在给定的质量速率下，流体压力的减小会增加系统的注入能力.因此注入能力随时间呈现先急剧减小、然后缓慢增加的趋势.

图5 热力作用与水力作用对裂隙开度的影响. (a) 总裂缝开度; (b) 裂缝开度改变量（水力作用）; (c) 裂缝开度改变量（热力作用）; (d) 注水量Fig.5 Influence of thermal and hydraulic effects on fracture opening: (a) total fracture opening; (b) change in fracture opening (hydraulic action);(c) change in fracture opening (thermal effect); (d) water injection volume

以上研究表明热力作用在促进裂缝开度的增大（从2.2×10-5m（0.1 a）增加到7.5×10-5m（10 a））和影响范围的延长方面（从30 m（0.1 a）延展到580 m（10 a））均起到了积极的作用.

3.3 裂缝间距对裂缝开度的影响

本文进一步采用THM模型研究了不同裂缝间距（半裂缝间距为100、50和25 m）对裂缝开度变化的影响. 图6显示了3种不同裂缝间距在注入时间为10 a时的温度分布. 由图6可知，随着裂缝间距的减小，模型的冷却范围逐渐增加. 当注入时间为10 a时，半裂缝间距为50 m的模型的冷却范围比100 m的更靠近模型的上边界，而25 m的模型已经达到了上边界. 同时，从图7(a)中可以看出，裂缝开度也随着裂缝间距的减小而增大. 当半裂缝间距为50 m时，注入点的裂缝开度比100 m时增大了20%左右；而当半裂缝间距为25 m时，该增大量则升至了约60%.

图6 不同厚度岩体在注入时间为10 a后的温度分布图Fig.6 Temperature distributions of rock masses with different thicknesses after 10 years injection

从图7(b)可以看出，随着裂缝间距的减小，热力作用对裂缝开度的增强效果逐渐增强. 当注入时间为10 a时，在裂缝间距为100 m的模型中，热力作用对裂缝开度的增强效果仅为水力作用的68%；而在裂缝间距为50 m的模型中，热力作用的增强效果却是水力作用的1.7倍；在25 m模型中，热力作用的增强效果则达到了水力作用的4.8倍.同时，降低裂缝间距还可以显著提高裂缝注水量.也就是说，尽管降低裂缝间距会造成水力作用增强效果的降低，但是热力作用对裂缝开度的增强却显著增大，以至于总的裂缝开度仍是显著增大的. 由于热储在垮落和运输至换热池的过程中会损失热量，因此在实际生产中应尽量减少裂缝间距，增加第一次采热降温的效率（一方面提升了整体采热效率，另一方面冷却了热储，改善了地下开采环境）. 如当半裂缝间距为25 m时，注入时间达到10 a后，温度降低区域已贯穿整条裂缝，即绝大部分热量都已采出.

图7 不同裂缝间距下裂缝开度变化趋势对比图. (a) 总的裂缝开度; (b) 裂缝开度改变量（水力作用和热力作用）Fig.7 Comparison of the change trends of fracture opening at different fracture spacings: (a) total fracture opening; (b) change in fracture opening(hydraulic and thermal effect)

增加基岩的冷却收缩和裂隙流体压力均能提升总裂隙开度. 但是当基岩冷却收缩起主导作用时，系统的注入能力提升；而当裂隙流体压力起主导作用时，系统的注入能力降低. 减小裂隙间距可以显著增加裂隙的冷却开度和总开度. 相反，增加裂隙长度可以提高裂隙中的流体压力而不改变基岩的冷却收缩，造成裂隙压力开度和总开度增加.虽然减少裂隙间距和增加裂隙长度均能改善总裂隙开度，但前者增强了系统的注入能力，而后者却削弱了注入能力.

4 结论

本文通过COMSOL Multiphysics多场耦合软件系统地研究了不同热储改造方式对热能提取效率的影响和地热系统运行期间的裂隙开度演化机理. 主要研究结论如下：

(1) 通过对比4种热储改造模式的换热效率和采热量发现，高渗透率热储的降温幅度最大，其次是随机裂隙热储，之后是随机裂隙+贯通裂隙热储，最小的是贯通裂隙和管道热储，这表明在相同的注入时间内，高渗透热储的热能提取效率最好.因此，在ESG-E热储致裂方面，应优化爆破/水力压裂参数，使干热岩尽量破碎，增加岩体-换热工质交换面积，提升换热效率和采热量.

(2) 热储裂隙开度演化受基岩冷却收缩和裂隙流体压力的竞争影响作用. 裂隙流体压力在运行前期主导裂隙开度演化，随着注入时间的增加，累计的基岩冷却收缩增加，并在运行后期逐渐成为裂隙开度演化的主导因素. 注入时间为1 a时，冷却开度只有压力开度的22%，当注入时间增加到30 a时，冷却开度增长到后者的164%.

(3) 增加基岩的冷却收缩和裂隙流体压力均能提升总裂隙开度；但是当基岩冷却收缩起主导作用时，系统的注入能力提升；而当裂隙流体压力起主导作用时，系统的注入能力降低. 减小裂隙间距可以显著增加裂隙的热力作用开度和总开度. 当裂隙间距减小到25 m时，热力作用开度增加为水力作用开度的4.8倍. 因此在EGS-E的热储分层致裂采热降温中，建议尽量减小层间距离，提升整体裂隙开度，从而提升换热效率和采热量.