深部矿井水平方螺旋形埋管充填体换热器及其耦合热泵系统性能研究

张 波，詹 睿，刘 浪，郇 超，赵玉娇，王 美

西安科技大学能源学院，西安 710054

矿产资源和能源是保证世界经济持续发展的基石，随着经济的发展对矿产资源和能源的需求不断增大，资源和环境形势十分严峻. 浅部资源的逐渐枯竭迫使国内外矿产资源的开采向地球深部进军，据不完全统计，国外超过千米深井矿山达到112座[1]，我国开采深度在千米以上的金属矿山也超过20座[2]. 地层温度随着深度不断增加，温度梯度通常在1.7～3 ℃/100米，据此计算千米以上深部矿井的岩层温度超过40 ℃，例如南非西部矿井采深3000 m，围岩温度约80 ℃[1]；徐州张小楼煤矿采深1010 m，岩层温度达到45 ℃[3]. 高岩温虽然会导致严重热害问题制约深部矿产开采，但也反映出深部矿井蕴藏着丰富的地热能资源，吸引众多学者围绕矿井地热能开采展开研究.

1989年加拿大Nova Scotia省Springhill镇的一个工业园利用当地废弃煤矿的矿井水结合热泵为建筑物供暖和工业过程提供热能[4]. 自此，以矿井作为天然热交换器利用矿井水提取地热能的方式迅速发展，在德国Freiberg、波兰Czeladz、挪威Folldal和英国Shettleston等地方开展了通过地源热泵利用矿井水实现供暖和制冷的实例[5–7]. 基于矿井水的地热应用属于开环系统，即将矿井水抽取至地面，提取热量后，再回灌至井下[8]. 这种方式虽然取热效率高，地热生产能力大，但是存在污染地下水层和引起地面沉降的风险，因此逐渐采用闭环系统[9]. 闭环系统是采用循环水或其他循环流体在嵌入地下的封闭换热管网提取地热能，可实现取热不取水，有效保护地下环境. 但是，也存在钻井费用较高和地下换热管的传热面积扩展困难等问题. 针对这些问题，Ghoreishi-Madiseh等[10]创新性地在矿井采空区充填前预先安置地埋换热管网，充填固结后则通过充填体实现地埋换热管网内工质与采场围岩之间的热交换，节约了地热钻井费用，有效扩展了地下换热管网的传热面积.实验和数值模拟结果表明该方法可实现地热能的可持续提取，为矿区提供清洁、廉价的可再生能源. 刘浪等[11]和张波等[12]在传统矿山充填基础上提出了矿山功能性充填的学术理念，并以此给出了矿床–地热协同开采总体方案，在充填过程中构建埋管充填体换热器 (Backfill heat exchangers, BHE)，实现了深部矿井充填开采、矿井降温和地热能开采的有机结合.

充填体作为人工蓄热储层与埋管换热管网耦合而成的地下换热系统性能与充填体热物性、换热管排布、换热管内部循环流体流态、水文条件等密切相关. 为了解决充填体蓄热速度和储能密度以及地热开采效能等关键问题，Li和Zhang[13]构建了全尺寸煤矿充填体内嵌换热管网的物理模型，通过数值模拟方法研究了其蓄热和释热的特性及其影响因素. 结果表明:某典型煤矿地下充填采场储能系统在每年冬季可提供约23 GWh热能，平均能量回收率为60%. 为了提高充填体蓄热能力，张小艳等[14]将管间充入相变材料的套管换热器埋入充填体，通过数值模拟研究发现管间添加相变材料可以提高充填体的蓄热能力，每立方米充填体10 h内平均蓄热增量比普通充填体增加约6800 kJ，总蓄热量在5 h内增加到90%. 基于相似理论，赵玉娇等[15]通过缩尺实验研究了换热管布置、管内流体流速、围岩温度对BHE释热性能的影响. 结果表明随着管间距、管长、流体流速和围岩温度的增加，系统的释热量均增加. 当采用蛇形管布置、管内流体流速0.7 m·s–1、围岩温度为35 ℃时，系统的总能效率最高. 赵玉娇等[16]利用天然鳞片石墨和钢渣等固体废弃物制备出充填材料.通过实验研究了充填体复合材料和围岩温度对充填体耦合换热器系统性能的影响. 与传统充填耦合换热系统相比，添加天然鳞片石墨的充填材料可将能量回收率提升60%以上. 沉降作用会影响采场充填体热物性的均匀性，郇超等[17]在充分考虑充填料浆在采场沉积特性基础上，通过三维CFD数值模型详细评价了非均匀充填体的换热特性. 研究表明孔隙率对充填体的换热性能有显著影响，且在有无渗流情况下的影响相反.

充填体内嵌换热管网的方式为利用矿井实现地热能存储和开采提供了新路径，被越来越多的研究机构重视. 但是，在以往的研究中多数采用常规的蛇形管布置，在提取地热过程中充填体势必出现明显的冷热端现象产生冷堆积问题而影响地热开采. 因此，本文借鉴在地板辐射供暖领域中通过螺旋形布管改善房间地板温度均匀性的经验[18]，提出一种方螺旋形埋管充填体换热器（Square-spiraltype backfill heat exchangers，S-S BHE）. 为了探讨S-S BHE的可行性，建立了BHE的三维非稳态数值模型，与典型蛇形BHE的综合性能进行了对比研究. 其次，详细分析了管内流速、管间距、地下水渗流速度和入口水温对S-S BHE及其耦合热泵性能的影响. 最后，对采用方螺旋形埋管充填体换热器耦合热泵系统实现供暖的生态效益进行了评估.

1 计算模型

1.1 物理模型

图1为埋管充填体换热器耦合热泵（Backfill heat exchangers coupled heat pump，BHECHP）系统示意图. 循环水在管内循环流动将矿井地热能提取至地面，经过热泵进一步提升温度后为矿区建筑供暖提供热能. 根据几何对称，构建了全尺寸SS BHE物理模型（如图2），主要包括充填体、围岩和埋管三部分，其中充填体为一个分层充填，换热埋管选用铜管. 根据量纲一边界扰动因子的影响因素分析[19]，确定了充填体两侧围岩计算边界，以保证数值计算结果的可控性. 具体的几何和位置尺寸如表1所示.

表1 模型几何条件Table 1 Model geometric conditions

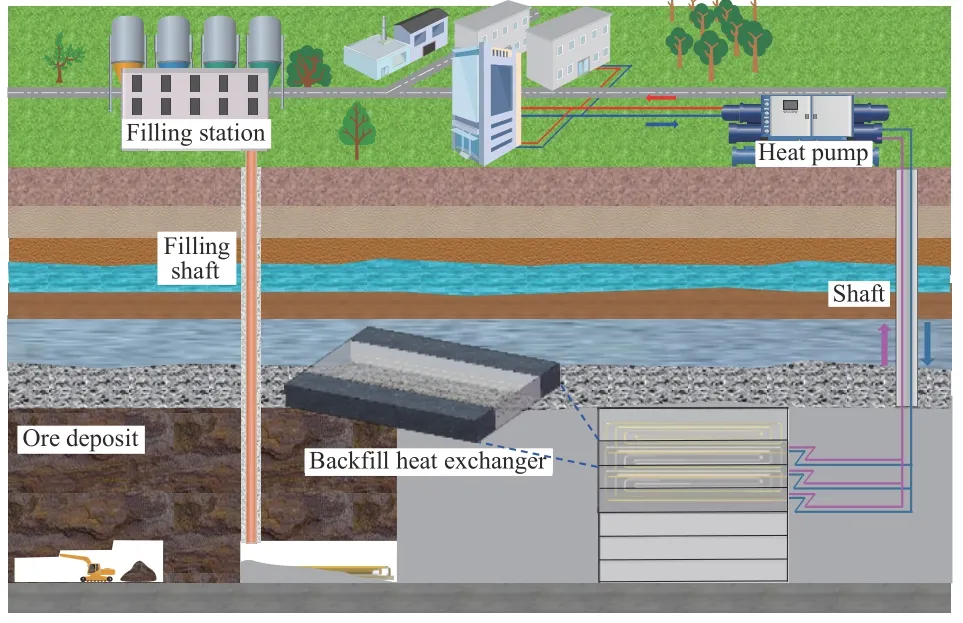
图1 BHECHP系统示意图Fig.1 Schematic diagram of BHECHP systems

考虑到数值计算量和计算精度，采用大型多物理场模拟软件COMSOL5.6模拟循环流体（水）、埋管、充填体和围岩之间在地下水渗流影响下的换热过程. 基于六面体结构和四面体混合网格对建立的三维物理模型进行网格划分，并对埋管及其毗邻区域网格加密，提高埋管与充填体之间传热计算精度，如图2（c）所示. 模型的相关热物性参数如表2所示.

表2 模型物理条件Table 2 Model physical conditions

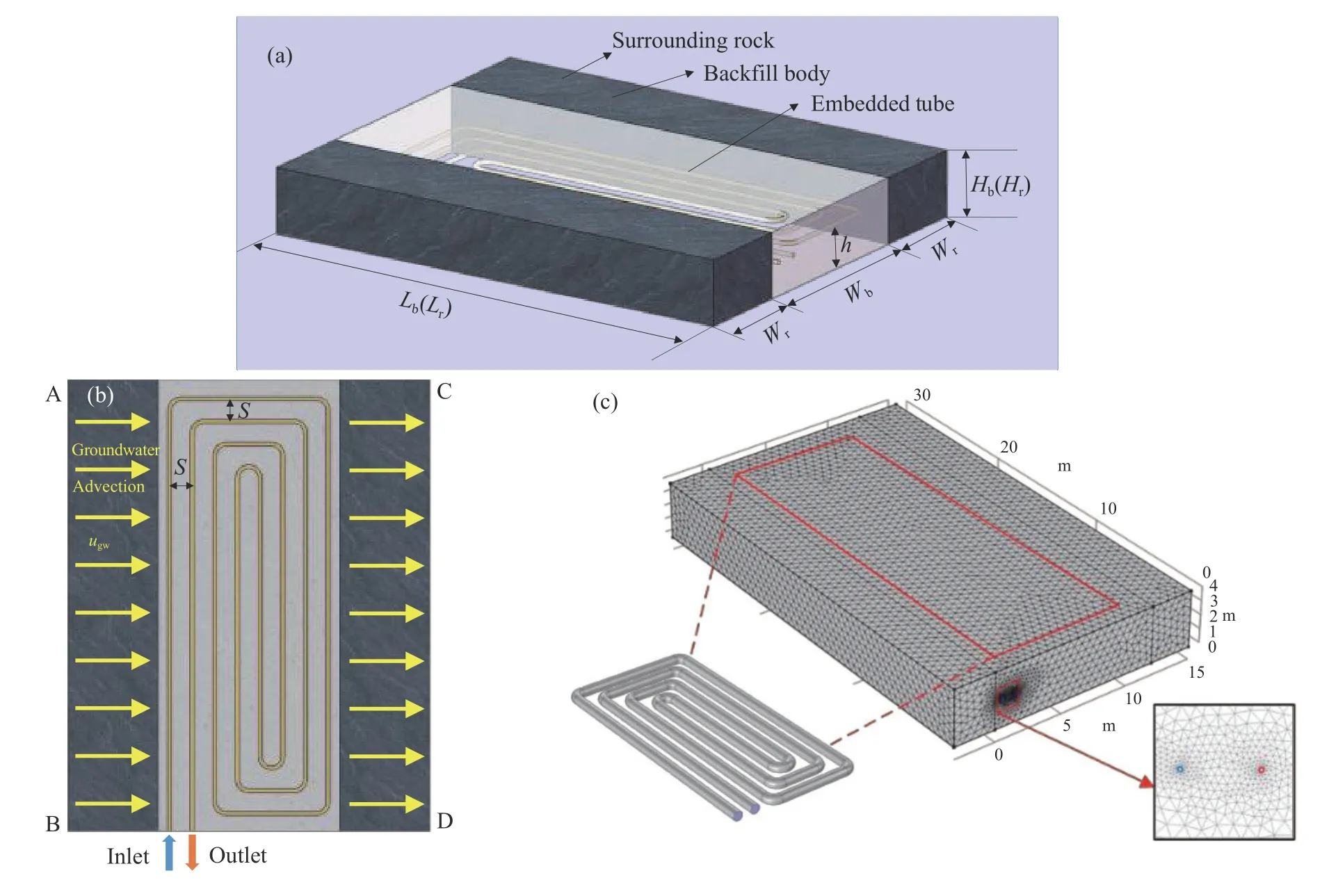
图2 S-S BHE物理模型与网格划分. (a) 3D物理模型; (b) 方螺旋管布置; (c) 物理模型网格划分Fig.2 Physical modeling and meshing of a horizontal S-S BHE: (a) 3D physical model; (b) square-spiral-type tube arrangement; (c) meshing of the physical model

1.2 数学模型

在地下水渗流影响下，埋管、充填体和围岩之间的换热是一个非常复杂的过程. 为了简化计算，本文做出了如下假设：①忽略埋管、充填体与围岩间的接触热阻；②充填体是各向同性的均匀、饱和多孔介质；③热物性参数在研究温度范围内保持稳定；④渗流地下水和循环流体均为不可压缩流体；⑤渗流过程服从达西定律；⑥地下水渗流方向沿水平方向；⑦地下渗流水与围岩或充填体之间处于瞬态热平衡状态，即地下渗流水与接触的充填体或围岩温度相同.

1.2.1 埋管的控制方程

连续性方程：

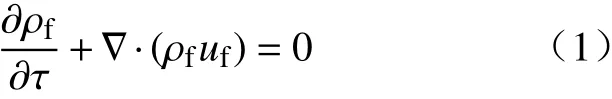
动量方程：

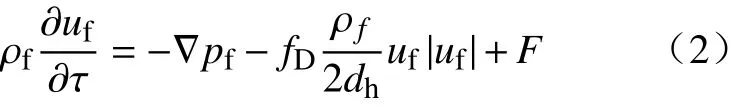
能量方程[20]：

式(1)～(3)中：τ为时间参数，s；ρf为管内循环水的密度，kg·m–3；uf为管内循环水的流速，m·s–1；pf为管内水头压力，Pa；Ap为管道的横截面积，m2；tf为管内循环水的温度，°C；fD为达西摩擦因子；F为体积力，N；dh为 平均水力直径，m；∇为梯度[20]；cpf为 管内循环水的比热容，J·kg–1· ℃–1；kr为埋管导热系数，W·m–1·°C–1；Qwall为通过管壁的换热量[20]，W·m–1.

1.2.2 充填体和围岩的控制方程

连续性方程[21]：

动量方程：

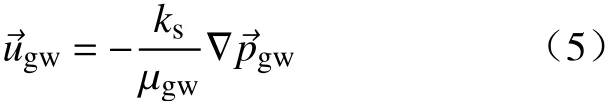
能量方程：

式(4)～(6)中：ρgw为地下渗流水密度，kg·m–3；T为地下渗流水温度，°C；ε为多孔介质孔隙度；为 地下水渗流速度，m·s–1；ks为充填体/围岩的渗透 率，m2；µgw为地下渗流水的动力黏度，Pa·s；Qm为质量源项，kg·m–3·s–1；为压强差，Pa；为等效体积比热容[21]，J·m–3·°C–1；分别为地下渗流水的体积比热容，J·m–3·°C–1；λeff为等效导热系数[21]，W·m–1·°C–1；Q为能量源项，W·m–3.

1.2.3 初始条件和边界条件

BHE设置在1200 m深部矿井采场内，根据中国大陆地温分布曲线推算出地温（t0）约为45 ℃[3].埋管及其内部计算区域：每个工况下的循环水入口温度和管内流速恒定，范围分别为8～20 ℃和0.06～1.2 m·s–1，默认温度10 ℃，默认管内流速为0.4 m·s–1. 围岩和充填体计算区域：AB和CD边界面（如图2(b)所示）的温度等于地温；其他边界面均为绝热面；渗流水进入围岩AB面时的温度等于地温，渗流速度恒定，范围为0～10–5m·s–1，默认渗流速度10–6m·s–1[22]. 充填体、围岩、埋管循环水和地下渗流水的初始温度均等于地温.

1.3 数学模型验证

1.3.1 独立性检验

在模拟计算之前，首先进行网格独立性和时间独立性验证，综合考虑计算工作量和计算精度，确定最佳网格数量和计算步长. 图3为模型独立性验证，图3（a）显示当网格数从290000升至800000时，运行第40、80和120天的计算结果平均偏差小于4.5%，因此网格数选取为290000. 图3（b）显示计算步长从1.0 d升至5.0 d，计算结果误差小于1%，因此计算步长选取为1.0 d.

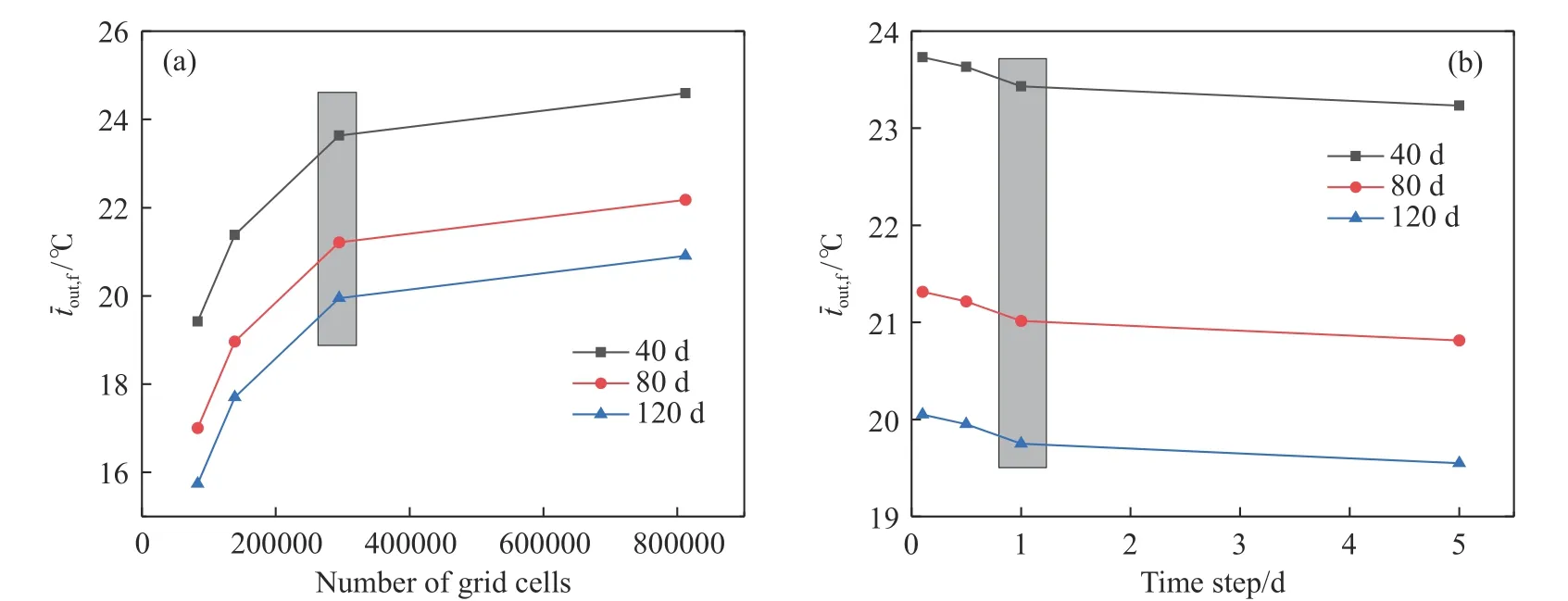
图3 数学模型独立性验证. (a) 网格独立性验证; (b) 时间步长独立性验证Fig.3 Mathematical model independence verification: (a) grid independence verification; (b) time-step independence verification

1.3.2 模型的验证

利用Guan等[23]和Chen等[21]的渗流条件下U形地埋管的实验数据，验证含地下水渗流的数值模型可靠性. 设置模型的几何参数、材料热物性、运行工况、边界条件和初始条件与上述两篇文献条件一致，模拟结果与实验结果对比如图4所示.可以看出模拟值变化趋势与实验值完全一致，模拟值与实验值之间的偏差在5%～–10%内. 因此，本文建立的数学模型具有足够的可靠性和精度.

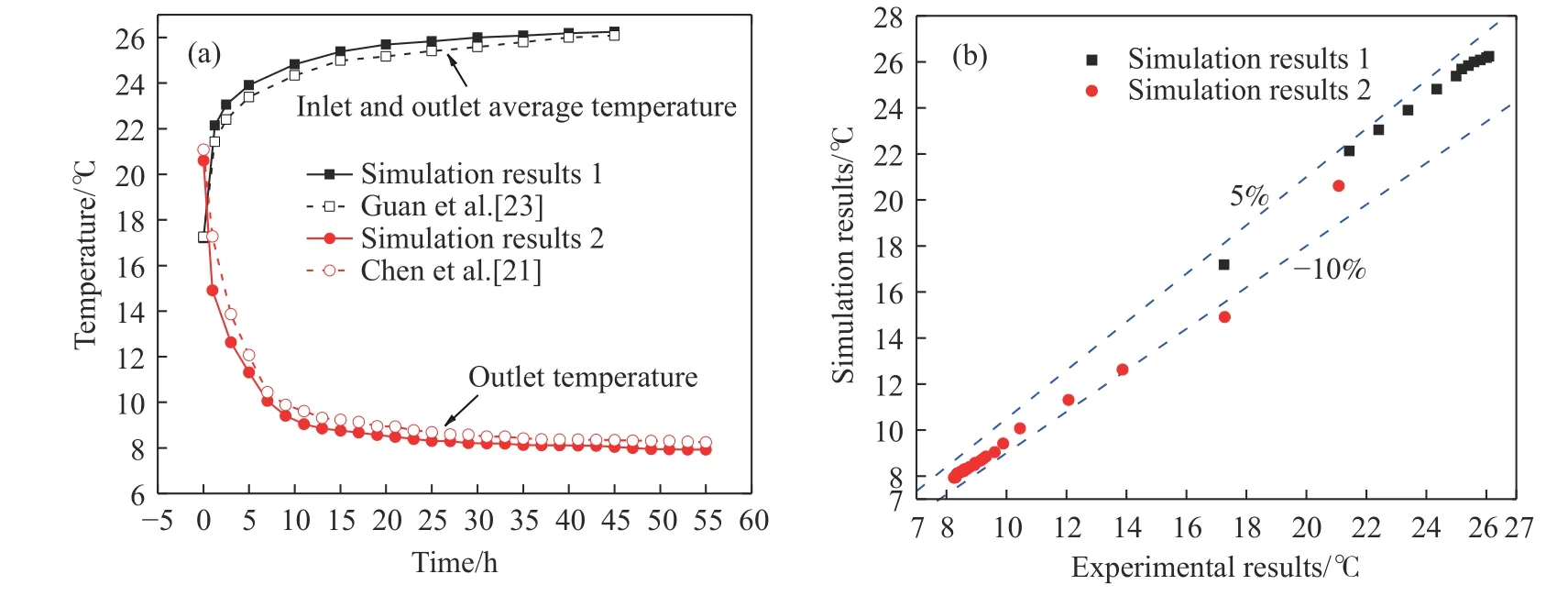
图4 模型准确性验证. (a)模拟值与文献实验值对比; (b)模拟值与实验值之间的偏差Fig.4 Model accuracy validation: (a) comparison of simulation values with experimental values from the literature; (b) deviation between simulation and experimental values

1.4 评价指标

1.4.1 单位管长平均换热功率

单位管长平均换热功率（）是一个采热周期内单位长度埋管的平均换热功率，W·m–1，反映了BHE提取地热的能力，由式（7）计算：

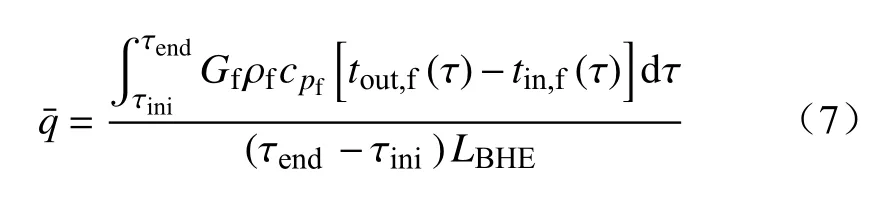
式中：Gf为管内循环水的体积流量，m3·s–1；tin,f(τ)、tout,f(τ)分别为管内循环水在BHE进、出口的实时温度，℃；LBHE为 埋管总长度，m；τini,τend分别为BHE换热的初始、结束时刻.

1.4.2 平均出口水温

平均出口水温（tout,f）是一个采热期内BHE出口水温的平均值，间接反映了BHE提取地热能的品质，由式（8）计算：

1.4.3 平均换热效能

平均换热效能（）的定义为一个采热期内BHE换热器实际总换热量与最大理论总换热量的比值，反应了BHE在一个采热期内的整体换热性能，由式（9）计算.

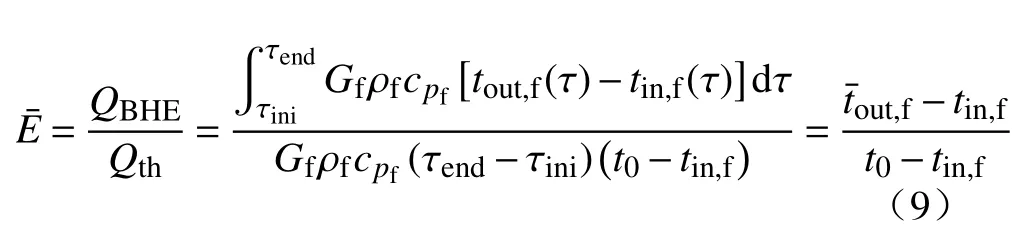
式中：QBHE为BHE换热器实际总换热量，J；Qth为BHE换热器最大理论总换热量，J；tin,f为BHE换热器入口水温，°C；t0为BHE换热器初始水温，°C.

1.4.4 制热季节能效

制热季节能效（Heating seasonal performance factor，HSPF）的定义是一个采暖周期的总供热量与总耗电量之比，综合反映了一个采暖季节能源利用效率的高低，由式（10）计算.

式中：Wpunp,BHE为BHE循环水泵[24]的实时功率，W. COPHP为热泵性能系数，近似与BHE出口水温成线性关系[25–27].Wcomp、Wpump,HP分别为热泵压缩机[28]、热泵循环水泵[28]的实时功率，W.QHP为热泵实时供热功率[28]，W. 依据地板辐射供暖要求设定热泵出水温度为40 ℃，根据德国制造商Dimplex提供的SI-30-TE型热泵的测试数据，COPHP=取a=0.092，b=3.85[28].

2 S-S BHE与蛇形BHE的性能比较

本节在相同运行工况和条件对比分析S-S BHE与两种典型蛇形BHE的换热特性. 三种BHE的充填体和围岩尺寸相同,如图5所示两种典型蛇形BHE分别为纵向蛇形埋管充填体换热器（Longitudinal-serpentine-type backfill heat exchangers，L-S BHE）和横向蛇形埋管充填体换热器（Transversalserpentine-type backfill heat exchangers，T-S BHE）.如表1所示，换热埋管内径25 mm，壁厚3 mm，管间距1 m，管长相同. 边界和模拟条件如下：循环水进口水温为10 ℃，循环水流速为0.4～1.2 m·s–1，地下水渗流速度分别取0、10–6和10–5m·s–1，地温为45 ℃，运行时间120 d.

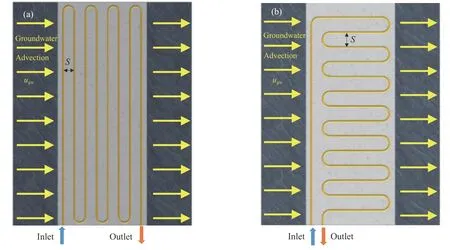
图5 典型蛇形管布置示意图. (a) L-S BHE; (b) T-S BHEFig.5 Schematic diagram of two typical serpentine tube arrangements: (a) L-S BHE; (b) T-S BHE

图6给出了120 d供热期内单位管长平均换热功率在不同渗流条件下随管内流速的变化. 从图中可以看出，S-S BHE的单位管长平均换热功率最大，略高于L-S BHE，而T-S BHE最小且差距明显. 随着渗流速度增大，S-S BHE换热能力的优势更加明显. 在无渗流情况下，S-S BHE换热功率比L-S BHE平均提高0.16 W·m–1，在渗流速度为10–5m·s–1时平均提高1.99 W·m–1. 在高渗流速度条件下，单位管长平均换热功率增幅较大，其中S-S BHE和L-S BHE换热功率增大的幅度大于T-S BHE.管内流速从0.4 m·s–1增大到1.2 m·s–1，S-S BHE、LS BHE和T-S BHE的单位管长平均换热功率，在渗流速度为10–6m·s–1时分别增加了6.41 W·m–1(19.96%)、6.48 W·m–1(20.62%)和5.67 W·m–1(18.48%)，在 渗 流 速 度 为10–5m·s–1时 分 别 增 加18.89 W·m–1(37.87%)、19.35 W·m–1(40.44%)和14.73 W·m–1(32.58%). 在相同管内循环水流速时，渗流速度对S-S BHE的单位管长平均换热功率正影响最大. 管内流速0.4 m·s–1时，渗流速度从10–6m·s–1增加到10–5m·s–1，S-S BHE、L-S BHE和T-S BHE单位管长平均换热功率分别增加17.79 W·m–1(55.41%)、16.44 W·m–1(52.31%)和14.50 W·m–1(47.21%).

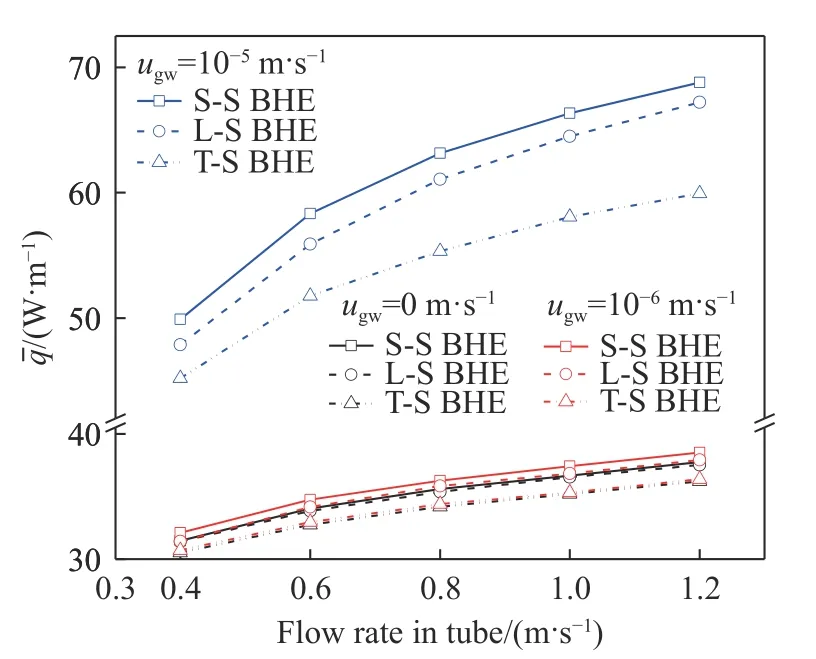
图6 120 d供热期内单位管长平均换热功率在不同渗流条件下随管内流速的变化Fig.6 Variations in the average heat transfer power per unit tube length with the flow rate in the tube at different groundwater advection conditions during a 120-day heating period

图7是120 d供热期内平均换热效能在不同渗流条件下随管内流速的变化. 可以看出，S-S BHE在不同工况下的换热效能始终最高. 渗流速度在0、10–6和10–5m·s–1情况下时，S-S BHE换热效能比随后的L-S BHE平均高出0.10%、0.41%和1.42%，随着渗流速度的提升，S-S BHE换热效能逐渐凸显. 另外，渗流对BHE换热效能有积极的影响，且对S-S BHE影响最大. 渗流速度从10–6m·s–1升至10–5m·s–1，S-S BHE、L-S BHE和T-S BHE换热效能分别提升12.04%～21.22%、11.66%～19.62%和9.62%～17.23%，管内流速越高，BHE换热效能

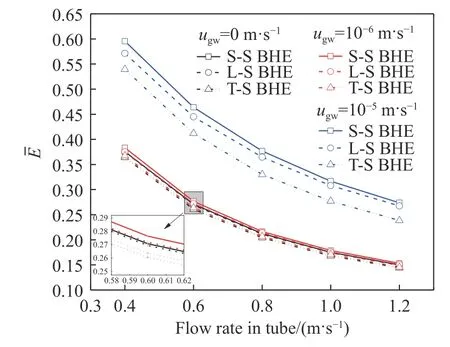
图7 120 d供热期内平均换热效能在不同渗流条件下随管内流速的变化Fig.7 Variations in the average heat transfer efficiency with the flow rate in the tube at different groundwater advection conditions during a 120-day heating period

的升幅越小. 从图中还可看出，BHE换热效能随着管内流速升高而降低，在高渗流环境下BHE换热效能降幅较大，且S-S BHE略高. 管内流速从0.4 m·s–1增加到1.2 m·s–1，S-S BHE、L-S BHE和TS BHE的换热效能，在渗流速度为10–6m·s–1时分别下降23.00%、22.42%和22.14%，在10–5m·s–1时分别下降32.18%、30.38%和30.11%.

3 计算结果与讨论

通过与蛇形BHE对比可以发现，S-S BHE在换热能力和换热效能表现出较优的特性，因此本节将对S-S BHE及其耦合热泵系统的运行特性进行详细的参数研究.

3.1 管内流速的影响

管内流速对换热器的换热能力和出口水温等性能参数影响明显，合理的流速非常重要[29]. 图8和图9分别为不同管内流速下S-S BHE的出口水温和单位管长换热功率随运行时间的变化曲线.从图中可以发现，出口水温和单位管长换热功率随运行时间不断降低，但下降速度逐渐趋缓，最终趋于某一数值. 120 d供热期内，管内流速越高，出口水温和单位管长换热功率的下降越明显. 管内流速0.06 m·s–1增加到1.2 m·s–1时，出口水温和单位管长换热功率的降幅分别从15.20%、19.54%增大到69.45%、74.63%. 另外，管内流速越高，出口温度和单位管长换热功率在运行初期下降的越快. 管内流速由0.06 m·s–1增加到1.2 m·s–1时，S-S BHE运行第7天的出口水温的降幅从1.62%升高至58.79%，单位管长换热功率的降幅则从2.08%增至42.14%. 当管内流速在0.1～0.4 m·s–1区间内时，出口水温和单位管长换热功率随管内流速变化明显. 分析其主要原因：管内流速在0.06 m·s–1和0.07 m·s–1时，循环水呈现层流状态，管内对流换热热阻与流速关系不大，另外循环水流速低有充足的换热时间，因此出口水温较高，单位管长换热功率较小，且两者的变化小. 管内流速在0.01～0.4 m·s–1范围内，循环水流动处于过渡区，流速升高会引起管内对流换热热阻明显降低，因此单位管长换热功率明显升高，出口水温明显下降则是因为循环水的管内换热时间缩短，埋管毗邻充填体温度下降等因素共同影响. 管内流速在0.6～1.2 m·s–1范围内，循环水流动处于旺盛湍流，管内对流换热热阻在总热阻的占比非常小，流速的增大对总热阻下降的贡献有限，因此单位管长换热功率略有升高，循环水的管内换热时间进一步缩短，导致出口水温有所下降. 综合考虑出口水温和单位管长换热功率，埋管的最佳管内流速为0.4～0.6 m·s–1，此时管内循环水处于从过渡区向旺盛湍流转变.

图8 不同管内流速下出口水温随运行时间的变化Fig.8 Variations in the outlet water temperature with the operating time at different flow rates in the tube

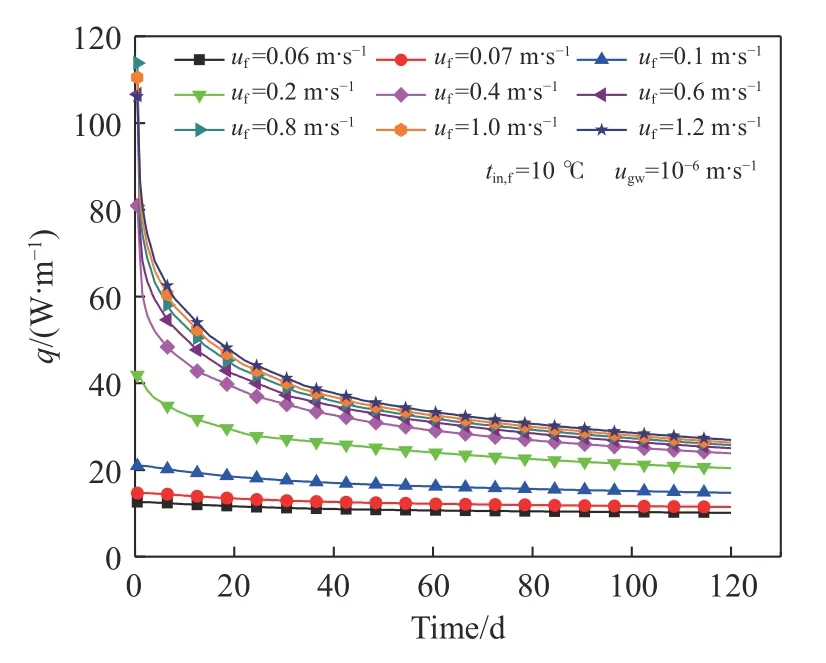
图9 不同管内流速下单位管长换热功率随运行时间的变化Fig.9 Variations in the heat transfer power per unit tube length with the operating time at different flow rates in the tube

图10为S-S BHE平均出口水温和单位管长平均换热功率随管内流速的变化. 可以看出平均出口水温和单位管长换热功率随管内流速分别呈现降低和升高的趋势，且变化幅度逐步减小. 在最佳管内流速区的平均出口水温和单位管长换热功率处于各自变化曲线的拐点附近. 管内流速从0.06 m·s–1升高到1.2 m·s–1，平均出口水温下降了24.94 ℃(61.89%)，单位管长平均换热功率提高了27.63 W·m–1(253.98%). 在最优管内流速区之前0.06～0.4 m·s–1和之后0.6～1.2 m·s–1的区域，管内流速每增加1 m·s–1，平均出口水温下降49.68 ℃和7.19 ℃，单位管长平均换热功率升高62.42 W和6.30 W，反映出管内流速在最优区域前后的影响差异非常明显.

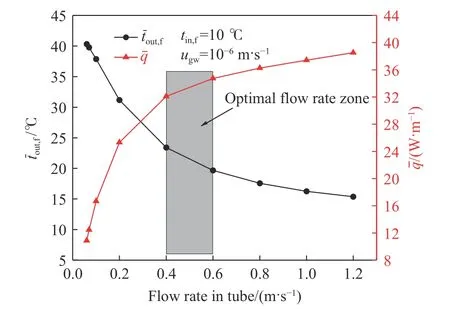
图10 平均出口水温和单位管长平均换热功率随管内流速的变化Fig.10 Variations in the average outlet water temperature and the average heat transfer power per unit tube length with the flow rate in the tube

图11是S-S BHECHP制热季节能效和S-S BHE平均换热效能随管内流速的变化. 随着管内流速的增加，制热季节能效和平均换热效能均呈现明显降低，其中平均换热效能下降更为显著. 从0.06 m·s–1增加到1.2 m·s–1，制热季节能效从7.56降低到4.70，降幅37.79%，平均换热效能从0.87下降到0.15，降幅达到82.30%. 管内流速过大对提高单位管长换热功率或降低对流换热热阻无明显效果[30]，反而会导致S-S BHE出口水温过低，严重降低了提取的地热能品质，进而降低热泵性能，功耗增加，最终反映到耦合系统的制热季节能效出现明显下降. 从图中可以看出，在0.4～0.6 m·s–1的最优管内流速范围，平均换热效能为耦合系统制热季节能效为5.60～6.01，远高于传统土壤源热泵2.1～3.4的制热性能[31].

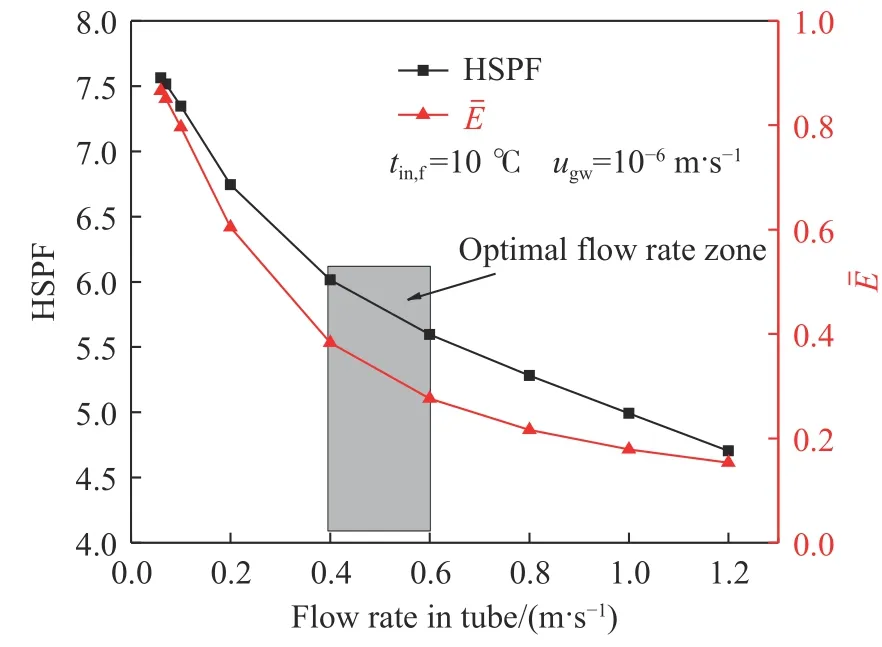
图11 制热季节能效和平均换热效能随管内流速的变化Fig.11 Variations in the HSPF and the average heat transfer efficiency with the flow rate in the tube

3.2 管间距的影响

管群换热性能受到充填体热阻和管间热干扰等因素的综合影响，而管间距是平衡充填体热阻和管间热干扰之间影响的关键参数. 图12和图13分别为不同管间距下S-S BHE出口水温和单位管长换热功率随运行时间变化的曲线. 管间距增大会引起S-S BHE出口水温下降，且在运行初期下降较明显而在运行后期降幅明显减小，单位管长换热功率正好相反. 管间距(S)从1.0 m增加到2.0 m时，出口水温在运行第7和120天分别下降了4.7和1.06 °C，差异明显，单位管长换热功率则分别提升了9.07和9.33 W·m–1，略有升高. 这主要是管间距的变化引起埋管总长变化所致. 从图13中还可以看出，管间距从1.0 m增加到1.5 m，单位管长换热功率提升明显，而在1.5 m至2.0 m范围内时变化不大.

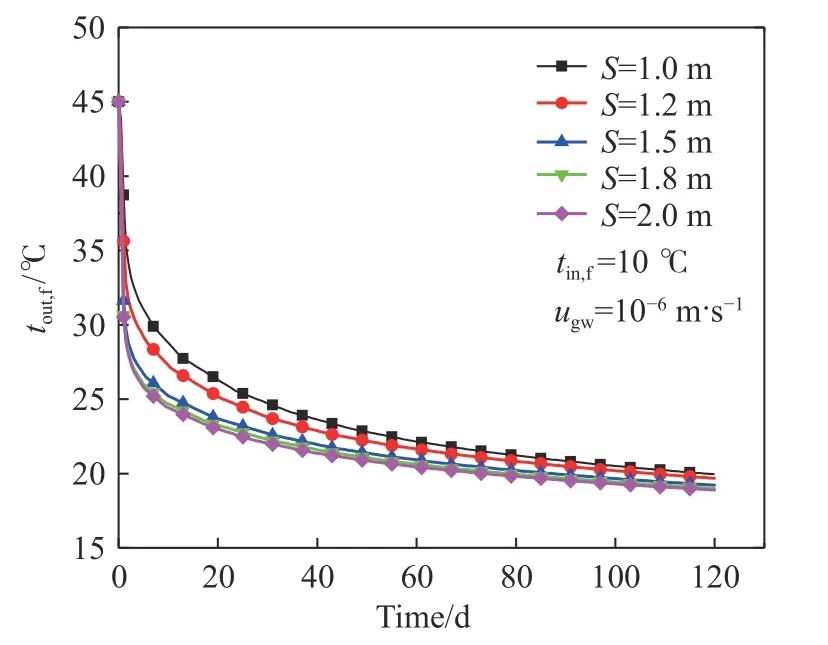
图12 不同管间距下出口水温随运行时间的变化Fig.12 Variations in the outlet water temperature with the operating time at different tube spacings

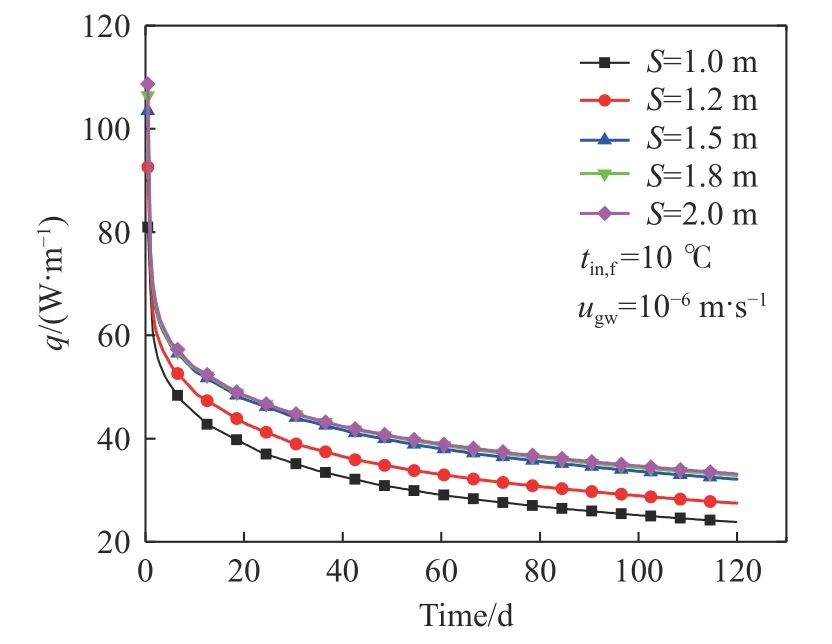
图13 不同管间距下单位管长换热功率随运行时间的变化Fig.13 Variations in the heat transfer power per unit tube length with the operating time at different tube spacings

图14 为S-S BHE平均出口水温和单位管长平均换热功率随管间距的变化. 如图所示，管间距在1.0～1.5 m和1.5～2.0 m两个范围内，平均出口水温分别下降1.65和0.52 ℃，单位管长平均换热功率平均升高8.88和0.94 W·m–1. 管间距增大，平均出口水温逐渐降低，但是单位管长平均换热功率没有出现Li和Zhang[13]描述的变化情况，即先增大后减小的趋势，峰值处为最优管间距. 其原因是本文中根据充填体的几何尺寸，能够形成方螺旋形布置的最大管间距为2 m，还未达到最优管间距，因此单位管长平均换热功率均成增长趋势，仅在大于1.5 m时出现涨幅减小的现象.

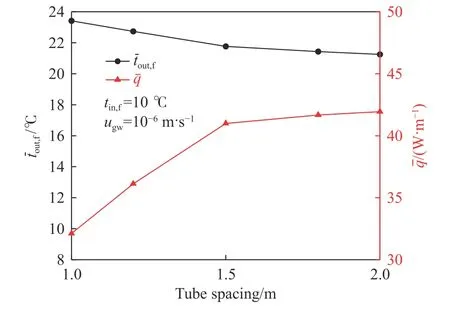
图14 平均出口水温和单位管长平均换热功率随管间距的变化Fig.14 Variations in the average outlet water temperature and the average heat transfer power per unit tube length with tube spacing

图15 为S-S BHECHP制热季节能效和S-S BHE平均换热效能随管间距的变化. 从图中可以看出，管间距增加会引起制热季节能效降低，但是下降有限，S-S BHE的平均换热效能降幅稍大. 管间距从1 m增加到2 m，制热季节能效仅下降3.59%，S-S BHE的平均换热效能下降了16.16%，这主要是管间距增加缩短了埋管管长引起出口水温降低所致.

图15 制热季节能效和平均换热效能随管间距的变化Fig.15 Variations in the HSPF and the average heat transfer efficiency with tube spacing

3.3 渗流速度的影响

地下水渗流可以明显提高地埋管的取热能力[32]. 因此有必要研究渗流速度对BHE及其耦合热泵系统性能的影响规律. 根据相关文献，渗流速度的数量级一般约为10–7～10–5m·s–1. 图16和图17为不同渗流速度下S-S BHE的出口水温和单位管长换热功率随运行时间的变化. 从图中可以看出，S-S BHE出口水温和单位管长换热功率均随着渗流速度增加而升高，且渗流速度越高越早趋于稳定，但是在低渗流速度时变化很小，甚至可以忽略不计. 渗流速度从5×10–7m·s–1增加到10–5m·s–1，运行第120天的出口水温从18.96 ℃升高至30.02 ℃，单位管长换热功率从22.10 W·m–1增加到47.94 W·m–1，渗流速度在5×10–7m·s–1时出口水温下降90%用时65.5 d，在10–5m·s–1时仅用17 d. 在0～10–6m·s–1的低渗流区，出口水温和单位管长换热功率在运行60 d内的变化几乎相同，在运行第120天时，出口水温变化小于1 ℃，单位管长换热功率变化小于2.5 W·m–1.

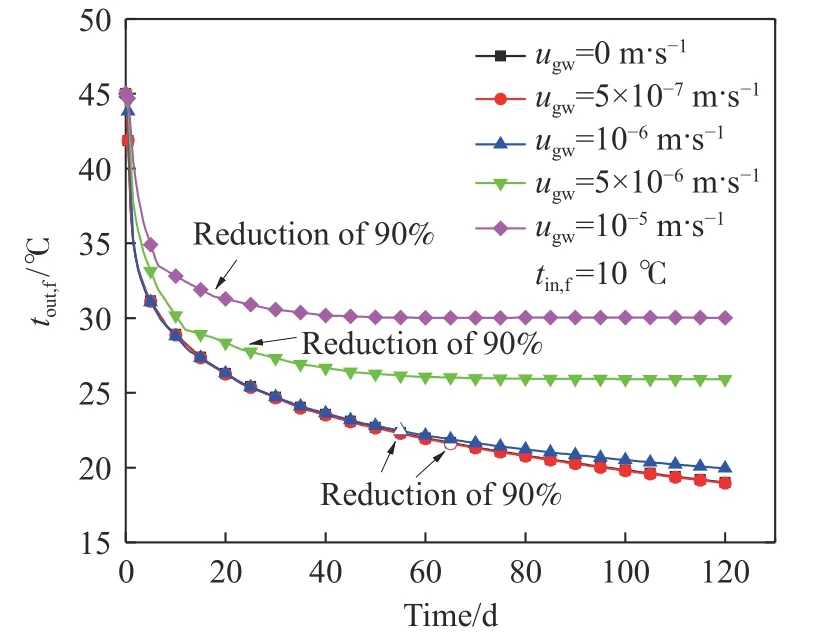
图16 不同渗流条件下出口水温随运行时间的变化Fig.16 Variations in the outlet water temperature with the operating time at different groundwater advection conditions

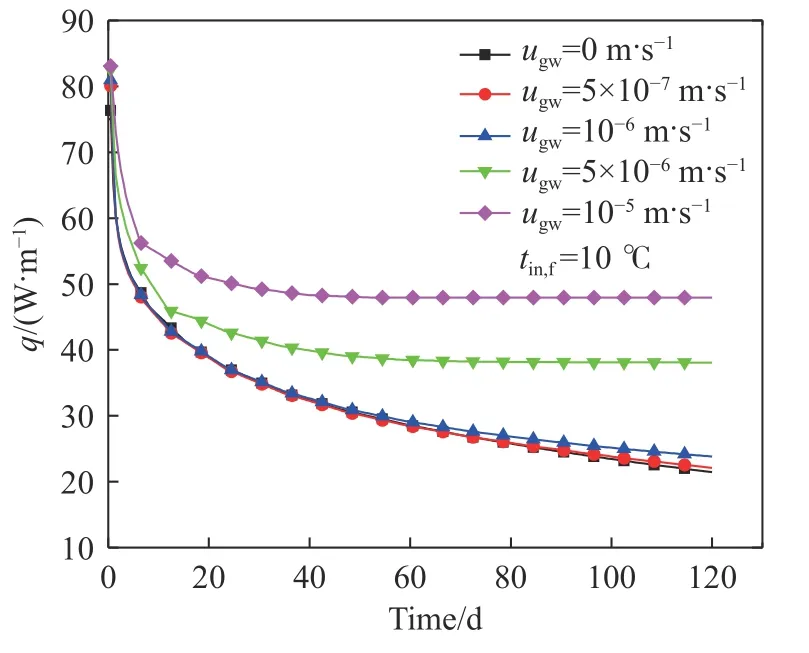
图17 不同渗流速度下单位管长换热功率随运行时间的变化Fig.17 Variations in the heat transfer power per unit tube length with the operating time at different groundwater advection conditions

图18为S-S BHE平均出口水温和单位管长平均换热功率随渗流速度的变化. 从图中可以看出，平均出口水温和单位管长平均换热功率随渗流速度呈线性递增趋势. 在5×10–7～10–5m·s–1常规渗流速度范围内，平均出口水温升高18.54 ℃，升幅59.16%，单位管长平均换热功率增长7.75 W·m–1，提高了33.54%，但是在0～10–6m·s–1低渗流速度区，平均出口水温提升0.33 ℃，单位管长平均换热功率增加0.81 W·m–1，变化很小.

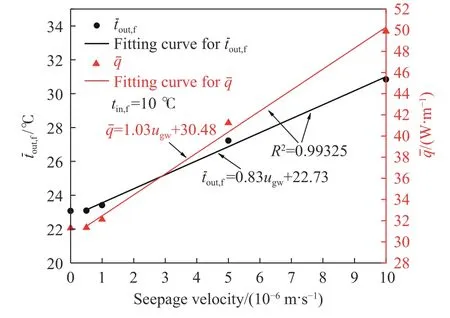
图18 平均出口水温和平均单位管长换热功率随渗流速度的变化Fig.18 Variations in the average outlet water temperature and the average heat transfer power per unit tube length with the seepage velocity

图19为S-S BHECHP制热季节能效和S-S BHE平均换热效能随渗流速度的变化. 从图中可以看出，渗流速度从0 m·s–1增加到10–6m·s–1，S-S BHECHP制热季节能效从6.00上升到6.01，仅增加0.23%，S-S BHE平均换热效能从37.36%升至38.32%，增加2.58%. 制热季节能效和平均换热效能在10–6～10–5m·s–1渗流范围内呈线性递增的趋势. 在10–5m·s–1渗流条件下，S-S BHECHP制热季节能效和BHE平均换热效能分别达到6.65和59.54%，比无渗流情况分别提升了10.90%和59.38%.

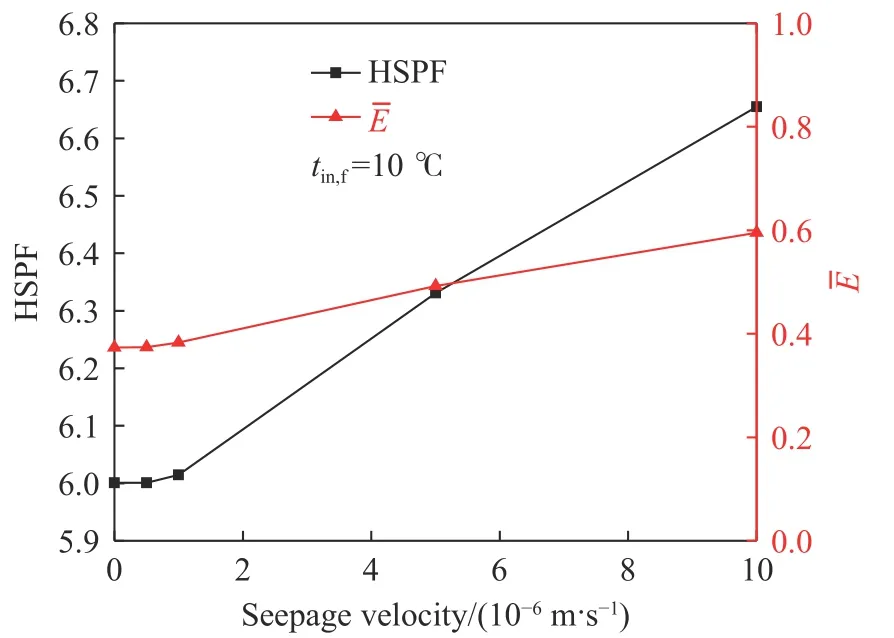
图19 制热季节能效和平均换热效能随渗流速度的变化Fig.19 Variations in the HSPF and the average heat transfer efficiency with the seepage velocity

3.4 入口水温的影响

入口水温变化会改变埋管与充填体之间的换热温差，进而影响BHE和BHECHP的整体性能.图20和图21分别为不同进口水温时S-S BHE出口水温和单位管长换热功率随运行时间的变化情况. 从图中可以看出，降低入口水温虽然可以增大循环水与充填体之间的换热温差，进而提高了单位管长换热功率，但是出口水温也相应下降，且运行时间越长温度下降越严重. 入口水温从20 ℃降低至8 ℃，在运行第7和第120天时，S-S BHE单位管长换热功率分别提高16.74和8.02 W·m–1，增幅均在48%附近，但是出口水温相应下降了14.63%和31.87%.

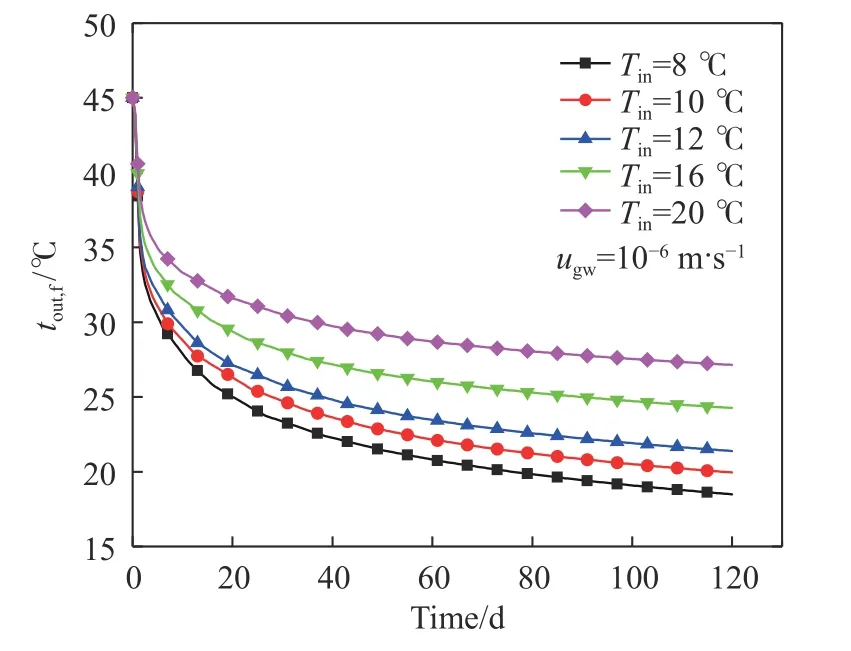
图20 不同进口水温时出口水温随运行时间的变化Fig.20 Variations in the outlet water temperature with the operating time at different inlet temperatures

图21 不同进口水温时单位管长换热功率随运行时间的变化Fig.21 Variations in the heat transfer power per unit tube length with the operating time at different inlet temperatures

图22 为S-S BHE平均出口水温和单位管长平均换热功率随入口水温的变化. 从图上可以看到，平均出口水温随入口水温线性增长，但单位管长平均换热功率正好相反. 入口水温在8～20 ℃范围内，每增加1 ℃，出口水温将升高约0.62 ℃，单位管长换热功率则下降约0.91 W·m–1. 其原因是入口水温改变了循环水与充填体之间的换热温差.

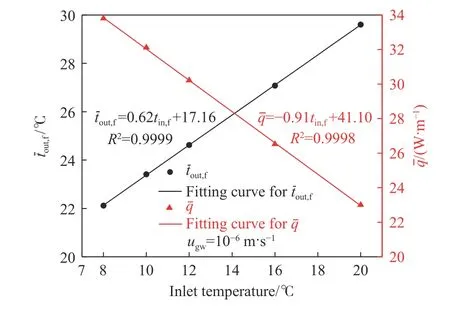
图22 平均出口水温和单位管长平均换热功率随入口水温的变化Fig.22 Variations in the average outlet water temperature and the average heat transfer power per unit tube length with the inlet temperature

图23 为S-S BHECHP制热季节能效和S-S BHE平均换热效能随入口水温的变化. 入口水温增加，制热季节能效呈线性提高，但是对平均换热效能影响不大. 当入口水温由8 °C增加到20 °C，制热季节能效从5.91上升到6.53，增加约为9.49%，但平均换热效能基本维持在0.38附近.

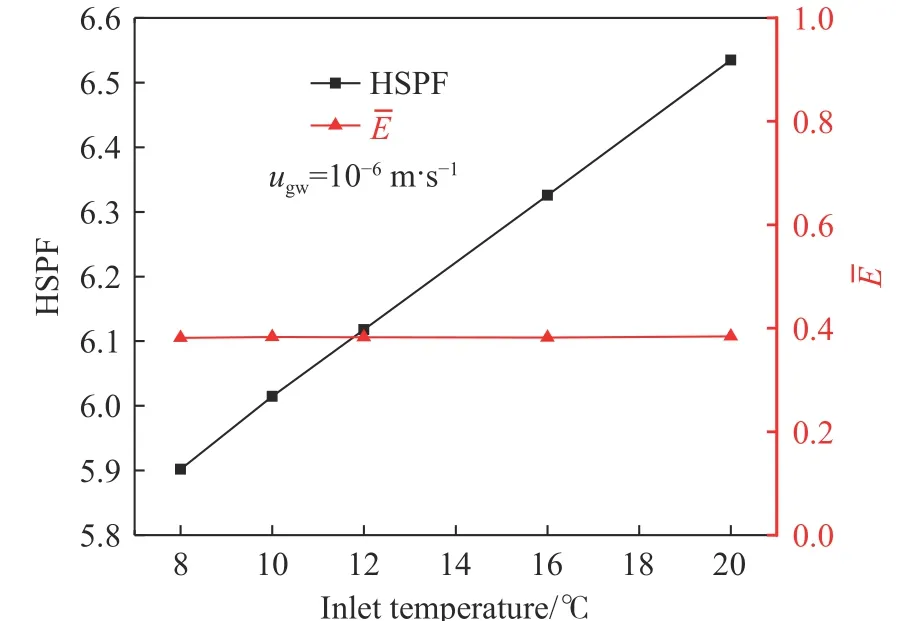
图23 制热季节能效和平均换热效能随入口水温的变化Fig.23 Variations in the HSPF and the average heat transfer efficiency with the inlet temperature

4 生态评价

节能降碳是我国“十四五”时期生态文明建设的重点战略方向，也是实现碳达峰碳中和目标的关键支撑. 本文将方螺旋形埋管充填体换热器耦合热泵（Square-spiral-type backfill heat exchangers coupled heat pump，S-S BHECHP）、燃煤锅炉（Coalfired boiler，CFB）、蓄热式电锅炉（Regenerative electric boiler，REB）、空气源热泵（Air source heat pump，ASHP）四种供热方式，从能耗和污染物排放量方面进行比较.

4.1 一次能源消费

忽略热网输送等损失，采用一次能源利用率计算单位供热面积年标准煤耗量：

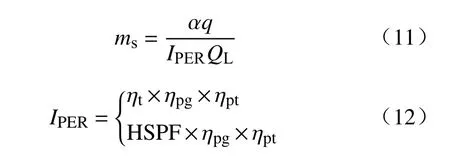
式（11）中：ms为单位供热面积年标准煤耗量，kg·m–2·a–1；IPER为一次能源利用率，如表3所示；α为供热时间，s·a–1；q为热负荷，W·m–2；QL为标准煤低位发热量，取29.3076 MJ·kg–1[33]；ηt为热效率；ηpg为发电效率；ηpt为电网输送效率.

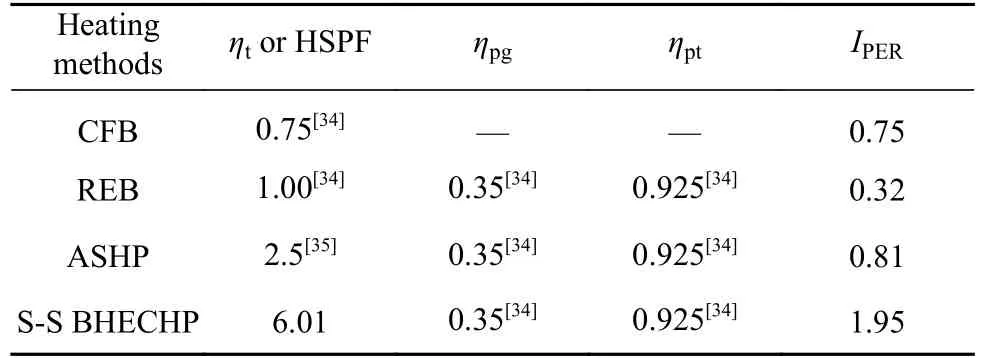
表3 不同供热方式的一次能源利用率Table 3 Primary energy efficiency of different heating methods

4.2 二氧化碳排放比较

我国能源活动引起的大气污染物主要有二氧化硫、氮氧化物、烟尘以及二氧化碳等[36]. 在实际应用计算中，为了简化起见，主要计算二氧化碳、二氧化硫、氮氧化合物等的排放量. 国家统计局及中国环境科学研究院资料研究表明，当1 kg标准煤燃烧会释放2.6 kg二氧化碳、0.024 kg二氧化硫和0.007 kg氮氧化物[37].

以我国黄河流域的严寒地区冬季供暖为例，单位面积热负荷取60 W·m–2[38]，供暖期为120 d，比较分析四种供暖方式的一次能源消费和二氧化碳排放. 图24为四种供热方式的单位供热面积年标准煤耗量和单位供热面积年碳排放量. 由此可见，采用S-S BHECHP供暖相比于其他三种传统供暖方式具有显著的节能降碳效果. S-S BHECHP的单位供暖面积年标准耗煤量和CO2排放量比REB、CFB和ASHP分别降低了83.39%、61.57%和56.84%. 以此计算，如采用S-S BHECHP替代最为常用的CFB供暖10万平方米，每年可节省标准煤4532 t，降低碳排放量1743 t.

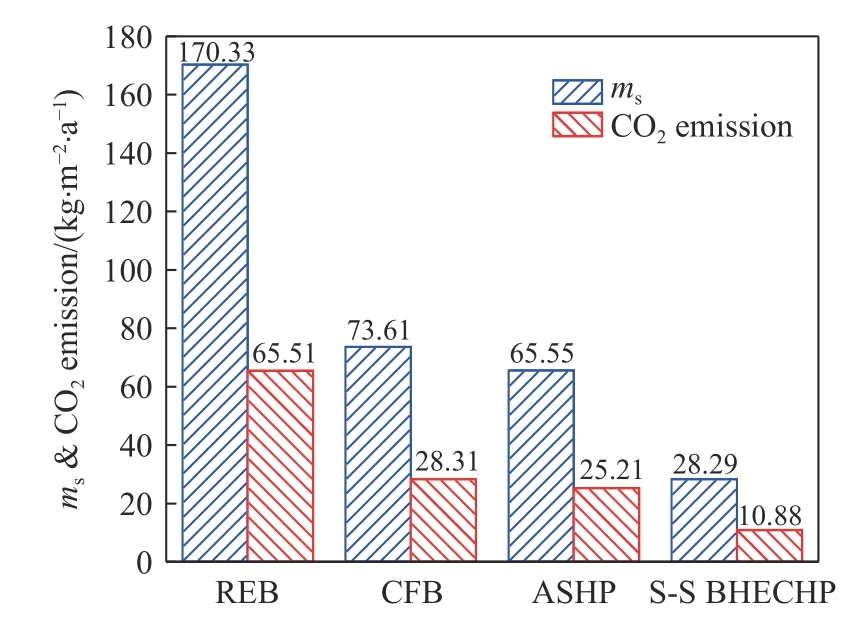
图24 四种供热方式的单位供热面积年标准煤耗量和单位供热面积年碳排放量Fig.24 Annual standard coal consumption and annual carbon emissions per unit heating area for the four heating methods

5 结论

(1) 针对在传统蛇形BHE在提取地热过程出现明显的冷热端现象产生冷堆积进而影响地热开采问题以及渗流对BHE的影响研究不足的现状.本文提出了一种水平S-S BHE，并基于达西定律构建了经过验证的三维非稳态传热–渗流耦合数值模型.

(2) 在相同几何条件和物理条件下，对比研究了S-S BHE、L-S BHE和T-S BHE的综合性能.发现S-S BHE展现了优良的性能，且较高渗流条件下的优势更加明显. 在无渗流情况下，S-S BHE单位管长平均换热功率比L-S BHE平均提高0.16 W·m–1，在渗流速度为10–5m·s–1，平均提高了1.99 W·m–1.

(3) 针对S-S BHE及其耦合热泵开展了详细的参数研究. 研究结果表明，管内流速和渗流速度对单位管长平均换热功率等四个综合评价指标的影响显著，而管间距和入口水温影响较小. 管内流速在0.06～1.2 m·s–1升高时，单位管长平均换热功率呈现前快后慢的增长趋势，但制热季节能效则相反，综合考虑发现最佳管内流速在0.4～0.6 m·s–1，此时管内循环水处于从过渡区向旺盛湍流转变.渗流速度对四个综合评价指标呈积极影响，但是在小于10–6m·s–1低渗流速度时影响很小，甚至可以忽略不计，在10–6～10–5m·s–1的中高渗流速度范围内，综合评价指标均随渗流速度线性递增.

(4) S-S BHECHP具有显著的降碳减排效果.对比研究结果表明，S-S BHECHP的单位供暖面积年标准耗煤量和CO2排放量比蓄热式电锅炉、燃煤锅炉和空气源热泵分别降低了83.39%、61.57%和56.84%. 采用S-S BHECHP替代传统燃煤锅炉供暖10万平方米，每年可节省标准煤4532 t，降低碳排放量1743 t.