基于肥尾效应的热带气旋迅速增强和路径突变研究
2022-09-29顾天红张艳梅
顾天红,许 可,杨 静,张艳梅,李 阳
(1.贵州省气象台,贵州 贵阳 550002;2.贵州省气象服务中心,贵州 贵阳 550002;3.贵州省黔西南布依族苗族自治州气象局,贵州 兴义 562400)
0 引言
热带气旋(Tropical Cyclone,以下简称TC)是最具破坏性的天气系统之一[1],其迅速增强(Rapid Intensification,RI)发展成强风暴后,总是伴随发生暴雨、风暴潮,造成严重的人民生命财产损失。对TC的强度和路径预报长期以来都是气象工作者研究的重点和难点[2-4]。自20世纪90年代后期以来,对TC的强度变化尤其是对影响其迅速增强的因素研究取得了诸多进展。如Holliday等[5]发现足够深的暖水、夜间发展、较小的台风眼尺寸有利于西北太平洋热带气旋的迅速增强。端义宏等[6]等发现环境气流、TC结构、海洋热状况变化等对TC强度变化有直接影响。金茹[7]分析发现TC的高空外流层对RI影响显著。薛霖等[8]研究发现台湾地形对台风Meranti(1010)的RI起重要作用。Bosart 等[9]通过分析台风Opal(1995)得出,对流层上层急流抽吸辐散增强、弱的垂直风切变、热量、水汽通量的共同增加会导致RI。DeMaria等[10]发现影响RI的有利因素包括弱的垂直风切变、弱的上层强迫和远的MPT。Jones等[11]研究了影响台风Erin(2001)强度变化的环境和内核条件。基于众多相关理论和试验,普遍认为TC的迅速增强一定是受某个特殊物理机制影响。
而KOWCH and EMANUEL[12]提出,既然TC迅速增强总是伴随着对流层上层某种特定机制,那只需识别出该机制即可证明存在迅速增强过程;反之,若迅速增强只是纯粹混沌内化的产物,其可预测性很小。同时,还指出基于统计学中的肥尾(Fat tail)效应,利用TC强度变化偏离正态分布的概率分布图来检验分析,若TC迅速增强过程的确有特定物理机制在起作用,则概率分布图上尾端会出现肥尾效应。并由此得出结论,在统计图的减弱一侧尾端出现肥尾,表明有特殊过程在TC的迅速减弱中起作用(排除登陆),而在TC增强一侧未见肥尾,故TC的迅速增强只是大尺度环境和自身连续强度变化的一部分,并无特殊机制作用。
此结论无疑是对前人研究的挑战和质疑,故本文基于众多已有研究成果,利用1988—2009年693个西北太平洋台风的最佳路径数据集与区域气候模拟资料作出TC强度变化的概率分布图,以期验证KOWCH and EMANUEL[12]的结论或其研究工作存在的瑕疵。同时,考虑TC的路径突变是小概率事件,相比强度变化的迅速增强而言,广大研究者对“特殊机制在TC路径突变中起作用”这一观点认同更高,故本文还将用此方法检验是否有特殊机制在TC路径突变中起作用。
1 资料与方法
1.1 资料
热带气旋数据采用2组。一组采用1988—2009年联合台风警报中心 (JTWC)西北太平洋(0~40°N,100~180°E) TC最佳路径数据集,包括6 h 1次的TC时间、经纬度位置、中心最低气压、中心附近最大海表面风速等;一组采用区域气候模拟资料6 h间隔记录,资料包括6 h 1次的TC中心经纬度、中心最低气压、近中心最大风速。考虑作图分析所需数据的同步性,本文选取1988年1月5日06时—2009年12月5日12时的693个TC进行研究。
1.2 肥尾效应
肥尾(Fat tail)效应,常译作肥尾、胖尾,统计学上按正态分布其两尾端都是很低的概率,但特殊情况下也会出现尾端极值分布,即偏离常态正态分布,尾端风险提升。著名的“黑天鹅事件”即罕见且破坏性大的事件,再如百年一遇的洪水等皆产生肥尾。

图1 肥尾分布示意简图Fig.1 The spatial distribution diagram of fat tail
1.3 模式与对流参数化方案简介
本文采用具有ARW核心(Skarmalock et al,2008)的WRF V3模型[14],该模型域以25°N,120°E为中心,在经纬方向上分别有232和196个网格点,水平间距25 km,有28个垂直高度。从1988年1月1日—2009年12月31日对模式进行积分,间隔为6 h。本文选取了目前数值预报模式中较为常用的3种对流参数化方案:KFMT(由南京大学中尺度灾害性天气教育部重点实验室的马雷鸣博士与谈哲敏教授合作开发)、KF(Kain-Fritsch)和SAS(Simplified Arakawa-Schubert)方案作为区域气候模拟的补充资料,关注不同方案对TC强度变化和路径变化的模拟差异。
1.4 TC迅速增强的定义和计算
目前国内外关于TC迅速增强的定义有多种[15]。Holliday[5]等利用SLP骤降42 hPa·day-1,约为增强阶段最强的25%。本文选取TC迅速增强的定义为24 h最大地面风速增强15 m·s-1。
TC强度变化概率分布图的横坐标为dv/dt,即TC的强度变化,纵坐标为概率P。值得注意的是,1 knot=1.852 km,最佳路径集里的时间间隔是6 h,而3种对流参数化方案资料里是1个单位代表6 h。故最佳路径数据集(best track)里的TC强度变化计算公式如下:
(1)
KFMT、KF和SAS 3种对流参数化方案下的TC强度变化计算如下:
(2)
1.5 路径突变的定义和计算
关于TC路径突变的定义也很多,Chan等[16]定义12 h内移向变化>20°为向右转折路径,移向变化<-20°为向左转折路径,移向变化在-10°~10°间为直行路径;董贞花[17]定义前后12 h平均移向右偏折角≥45°由偏西行或西北行突然转向偏东行或东北行为突然东折。本文参考85-906攻关项目[18]中TC路径突变的标准为:12 h内左折角度≥30°或右折角度≥45°。
TC路径突变的概率分布图,横坐标为偏折角度dθ,纵坐标仍为概率P。参考戴高菊等[19]关于TC路径偏折角度θ的计算如下:
(3)
利用球面距离公式计算距离:
L=α×R
(4)
其中α=arccos(cosa1cosa2cos(b2-b1)+sina1sina2),R=6371 km,a1、b1、a2、b2分别为A、B 2点经纬度。
TC折角计算[23]:12 h内的偏角,利用偏折角度公式计算每1、2和2、3时次组成的2个向量的夹角。图2为TC路径突变示意简图。
2 区域气候模拟的TC强度变化的概率分布
结合表1和图3分别给出KFMT、KF和SAS 3种不同对流参数化方案模拟的TC强度变化概率分布,可以看出,观测值(best-tracks)左右两端均有肥尾效应,当挑选出符合RI标准的TC再分析时,发现观测值尾端偏折(肥尾趋势)更明显,即决定台风的RI过程和非RI过程的物理机制是有差异的,否则图3里的观测值线偏折趋势应一致,这也说明,肥尾效应确实可以作为TC迅速增强过程是否受特殊物理机制支配的判据之一。 基于合理分析,本文提出猜测,可能是文献[15]所选取的样本数过大而掩盖了不明显的肥尾效应,即结果被平均,而肥尾在本文的缩小样本中却较为明显。

图2 TC路径突变示意简图Fig.2 The diagram of Tropical Cyclone path mutation
与观测值对比可以看出,无论是KFMT、KF还是SAS方案的模拟结果(圆圈黑线)在TC减弱阶段均有明显肥尾,而在增强阶段完全没有(TC个数均为0),即3个方案对TC强度RI的模拟能力都很弱。同时,KFMT方案对TC的强度变化(非RI)模拟效果最好,KF方案次之,SAS方案最差。
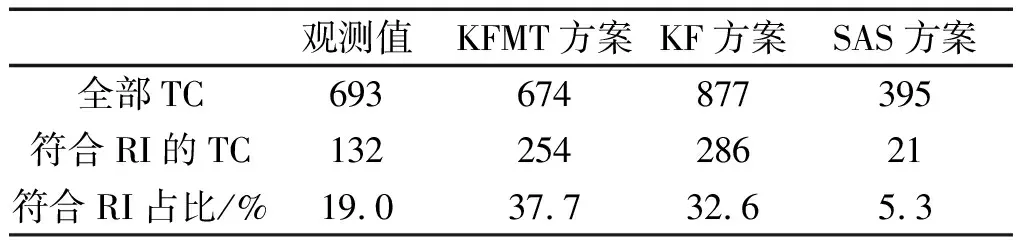
表1 3种方案下识别全部TC和符合RI标准TC的情况Tab.1 The details of all TC and the TC match condition of RI in the three Convection parameterization
3 区域气候模拟的TC路径偏折的概率分布
结合表2,从KFMT、KF、SAS 3种方案对TC路径偏折的概率分布(图略)可以看出,无论是实况还是模拟、路径左偏还是右偏,3种方案对TC路径偏折的模拟都较好,差异不大,且两端皆有较明显的肥尾效应,这表明TC的路径突变确实是有特殊物理过程在起作用。本文继续挑选出符合路径突变标准的TC进行分析,发现无论实况还是模式、左偏还是右偏,两端肥尾效应略有增加。分别对比RI筛选前后的图4,发现总体趋势不变,但筛选后的约等于整体略向上平移。

图3 方案KFMT(上)、KF(中)、SAS(下)全部(a、d、g)、符合RI(b、e、h)和挑选后一般增强(c、f、i)的TC强度变化概率分布Fig.3 The intensity change probability distribution diagram of All(a、d、g),RI(b、e、h),the rest of TC(c、f、i) in the KFMT(up),KF(middle),SAS(down)
本文还通过不断提高路径突变的偏折角度阈值,发现这种平移间距离会随着筛选条件的严苛即符合路径突变台风个数的减少而呈逐步扩大趋势。
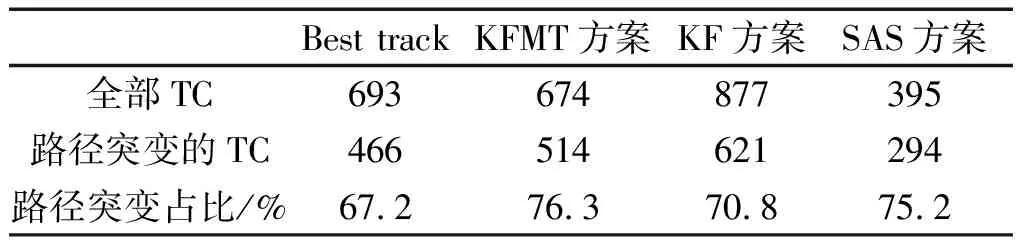
表2 3种方案下识别全部TC和符合路径突变标准TC的情况Tab.2 The details of all TC and the TC match condition of path mutation in the three Convection parameterization
4 结论
① KOWCH and EMANUEL(2015)的结论有瑕疵之处,决定TC的RI过程和非RI过程的物理机制是有差异的。
②肥尾效应在TC路径突变中比在TC迅速增强中更明显。
③不同对流参数化方案对TC的强度变化模拟不同,其中KFMT方案模拟效果最好,KF方案次之,SAS方案最差。但无论是KF、KFMT还是SAS方案,对TC强度迅速增强的模拟能力都很弱,但在减弱阶段均能较好模拟。
④ 3种方案对TC路径偏折的模拟都较好,两端皆有较明显的肥尾效应,表明TC的路径突变确实是有特殊物理机制在起作用。
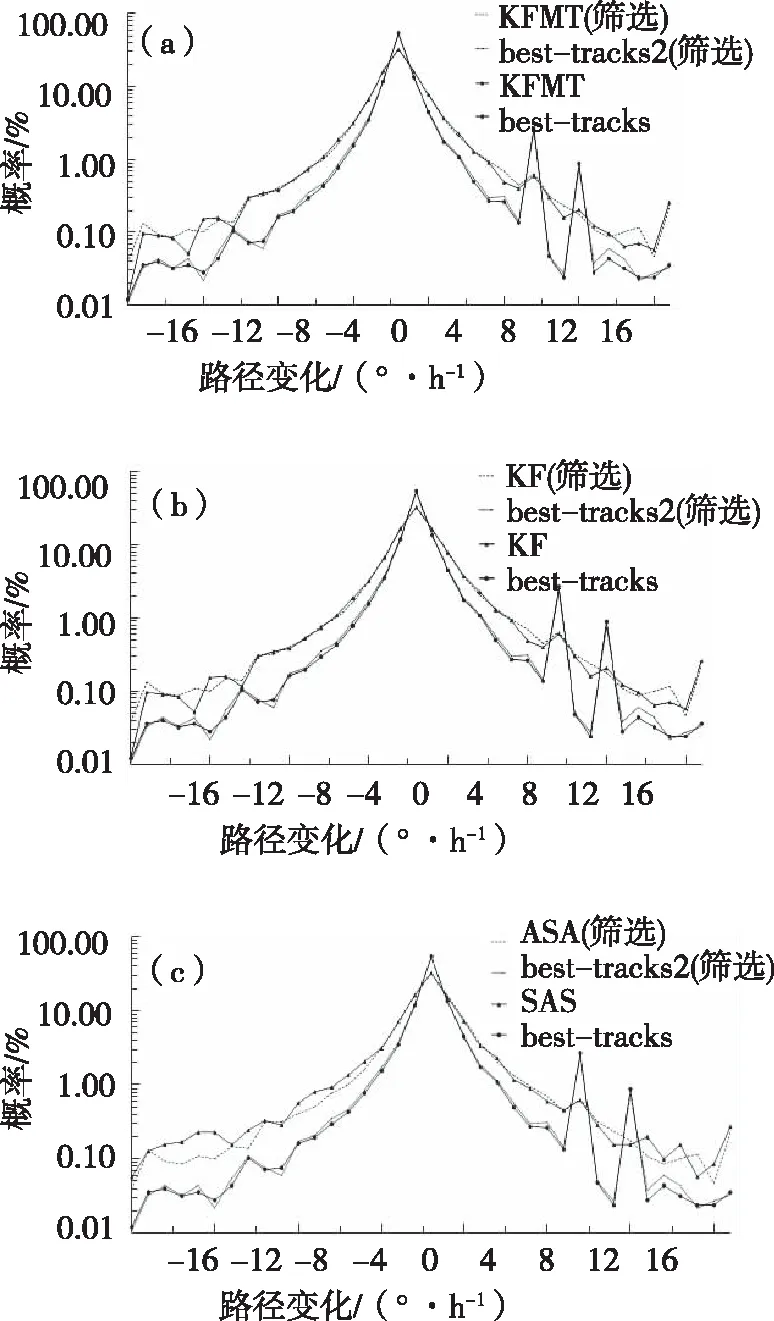
图4 KFMT(a)、KF(b)、SAS(c)方案下TC筛选前后路径偏折概率分布Fig.4 The path mutation probability distribution diagram of TC before and after comparison in the KFMT(a),in the KF(b) and in the SAS(c)
