一种区间二型T-S模糊模型辨识算法

尹 健

（华能国际电力江苏能源开发有限公司 南通电厂，江苏 南通 226001）

0 引言

由if-then规则描述的T-S模糊模型，其后件部分为线性表达式，在非线性系统的模糊模型辨识与控制方面具有较大的优势[1]。模糊聚类是一种无监督学习算法，针对给定数据集，根据一定的寻优算法将数据自动分为若干类。因此，模糊聚类经常应用于T-S模糊模型的辨识，聚类数目即T-S模糊模型的规则数。其中，模糊C均值聚类（Fuzzy c-means，FCM）算法是应用较多的算法[2-4]。

由于一型模糊逻辑系统（Type-1 fuzzy logic systems，T1-FLS），其隶属度函数的值为确定值，不能够处理实际非线性系统的不确定特性。针对这一缺陷，Zadeh提出了一种新的模糊集合，即二型模糊集合（Type-2 fuzzy sets，T2-FS）[5]。二型模糊集合与传统一型模糊结合的区别就在于隶属度函数的描述方面，二型模糊集合的隶属度由首隶属度和次隶属度构成。首隶属度与传统一型模糊集合一样，是输入变量的函数，一般可选择三角函数、高斯函数等；次隶属度由输入变量和首隶属度确定。

二型模糊集合分为区间二型模糊逻辑系统和普通二型模糊集合，区别在于两者的次隶属度函数。区间二型模糊集合的次隶属度定义为1，而普通二型模糊集合的次隶属度为函数。由于区间二型模糊集合的计算比较简单，不仅在控制系统中得到了大量应用[6-8]，也应用于区间二型模糊C均值聚类（Interval type-2 fuzzy c-means，IT2-FCM）算法[9]。区间二型模糊集合与传统一型模糊集合的差别在于其存在一降阶过程，一般采用Karnik-Mendel （KM）降阶算法[10]。KM降阶算法是一重复迭代过程，其计算过程耗时较多，不适用于实时控制系统。

为了克服传统KM降阶算法的缺陷，相关文献中研究了多种提高KM降阶效率的算法，比如EKM[11]，IASC[12]，EIASC[13]等。虽然这些算法提高了KM降阶算法的效率，但其本质上也是迭代算法。本文采用一种直接降阶算法BMM算法[14]，并将其应用于IT2-FCM聚类算法的降阶过程，避免了区间二型模糊集合降阶过程中的迭代过程，提高了IT2-FCM聚类算法的降阶效率。其次，根据IT2-FCM聚类算法对T-S模糊模型的输入空间进行划分，得到了区间二型T-S模糊模型，并进行前件参数的辨识。最后，利用最小二乘算法进行T-S模糊模型的后件参数辨识，通过两个典型的非线性系统的辨识结果验证了本文算法的有效性和实用性。

1 区间二型T-S模糊模型

与传统T-S模糊模型类似，区间二型T-S模糊模型也由if-then规则来描述。根据前件形式和后件形式的不同，区间二型T-S模糊模型有3种形式，分别为：前件为区间二型模糊子集，后件为确定值；前件为一型模糊子集，后件为区间值，以及前件为一型模糊子集，后件为区间值。本文采用第一种形式，则第i条模糊规则描述如下：

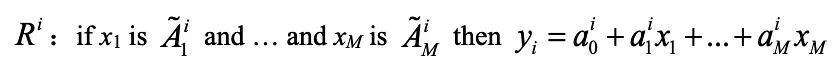
针对第k个采样时刻的输入向量xk，设第i条模糊规则的激发隶属度高、低限分别为，则T-S模糊模型的输出可根据KM降阶算法得到。为了简化，一般利用高、低限的平均值，表示如下：

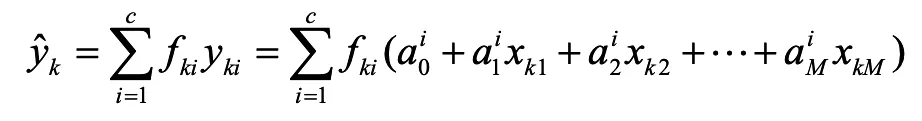
其中：

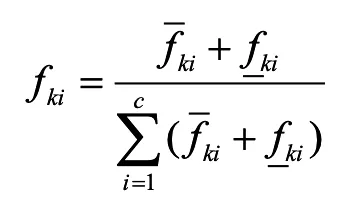
2 本文算法

2.1 区间二型模糊C均值聚类

模糊C均值（Fuzzy c-means，FCM）聚类算法是硬C均值聚类（Hard c-means，HCM）算法的拓展。将模糊隶属度引入聚类算法，克服了传统HCM聚类算法非0即1的缺陷，更符合实际人们的认知系统。FCM聚类算法定义了样本属于某一类别的隶属度的概念，可用uik来表示，i表示聚类的标识，k表示样本的标识。传统模糊C均值聚类算法的目标函数如式（1）。

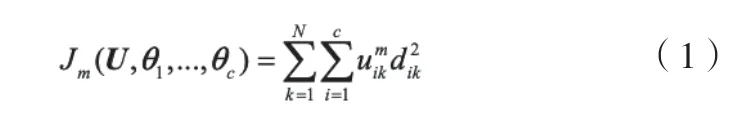
其中：dik为样本xk到聚类中心θi的欧式距离；加权指数m是算法的关键参数，m取大于1的实数，一般m选择2。聚类的最终结果是得出目标函数Jm的极小值，并满足式（2）的约束条件。

根据拉格朗日乘子法，FCM样本隶属度和聚类算法中心的迭代计算公式如式（3）和式（4）。

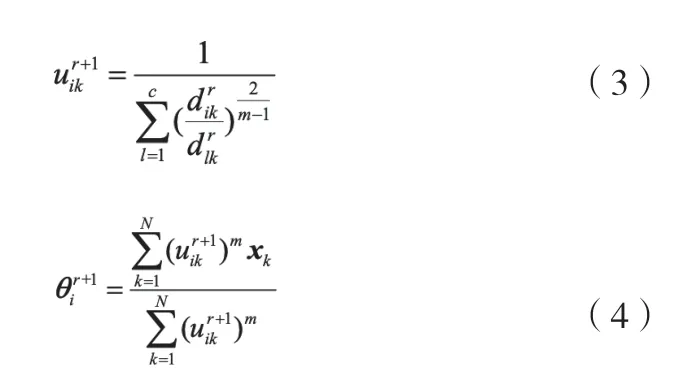
区间二型模糊C均值聚类算法设置两个m值，分别为m1和m2，其聚类目标是最小化如式（5）的两个目标函数[9]。

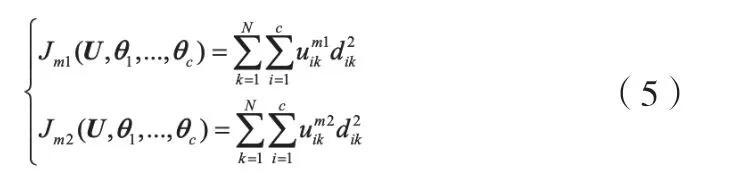
区间二型模糊C均值聚类隶属度的高、低限表示如式（6）和式（7）。

聚类中心θi则通KM降阶算法得到，具体的算法流程可参考文献[9]。

2.2 算法流程

本文采用一种直接降阶算法——BMM降阶算法，避免了KM降阶算法的迭代过程。将其应用于区间二型模糊C均值聚类算法的降阶过程，聚类中心的计算过程如式（8）。

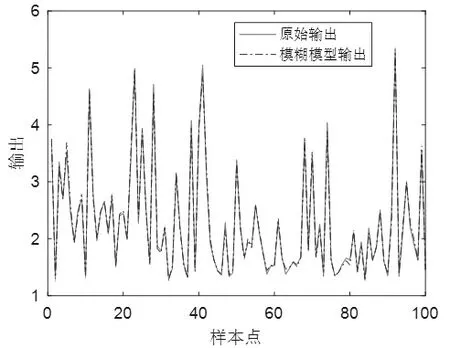
图1 模糊模型与原始输出曲线（实例1）Fig.1 Fuzzy model and original output curve (Example 1)

其中：0≤n≤1。

基于区间二型模糊C均值聚类算法的T-S模糊模型辨识流程描述如下：

1）针对N对训练数据(xk，yk)，设置聚类个数c（也即模糊规则数），参数m1、m2、n，算法结束阈值ε，算法的最多迭代次数rm，随机初始化聚类中心θi0，设迭代计数器r=0。

2）根据式（6）和式（7）计算样本隶属于第i个聚类的隶属度的高、低限。

3）根 据 式（8）计 算θi(r+1)，如 果||θi(r+1)-θi(r)||或 者r＞rm，则退出算法，执行步骤4），否则继续执行步骤2）。

4）根据最小二乘算法计算T-S模糊模型的后件参数。

3 仿真实例

3.1 仿真实例1

本例选取如下非线性方程：

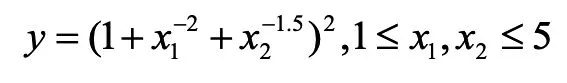
该方程共有100组数据，前50组作为训练数据，后50组作为验证数据。辨识参数设置如下：模糊规则数c=6，m1=2，m2=3，n=0.2。图1和图2分别为辨识结果的输出曲线和误差曲线。

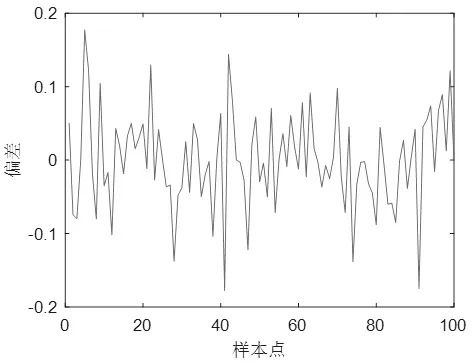
图2 模糊模型与原始输出误差曲线（实例1）Fig.2 Fuzzy model and original output error curve (Example 1)

3.2 仿真实例2

本例选取如下非线性离散模型：

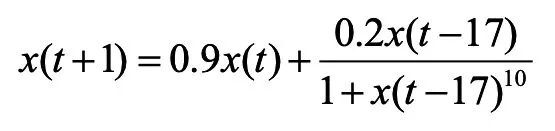
该模型共产生1000组数据，前200组作为训练数据，后800组作为验证数据。辨识参数设置如下：模糊规则数目c=2，m1=2，m2=3.5，n=0.4。图3和图4分别为辨识结果的输出曲线和误差曲线。

4 结论

区间二型模糊集合常用的KM降阶算法，其计算过程繁琐，并不适合于实时控制系统。目前，已有多种直接降阶算法来代替KM降阶算法。本文将BMM降阶算法应用于区间二型模糊C均值聚类，提高了区间二型模糊C均值聚类算法的实时性。在此基础上，利用区间二型模糊C均值聚类进行T-S模糊模型的输入空间划分，建立了区间二型T-S模糊模型。仿真实验表明，本文算法的辨识精度较高，并可用于实时建模与控制。在实际应用的时候，可根据对象特性选择合适的m1，m2以及n值，以得到较好的辨识效果。

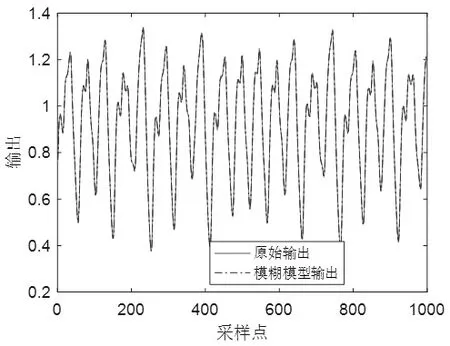
图3 模糊模型与原始输出曲线（实例2）Fig.3 Fuzzy model and original output curve (Example 2)

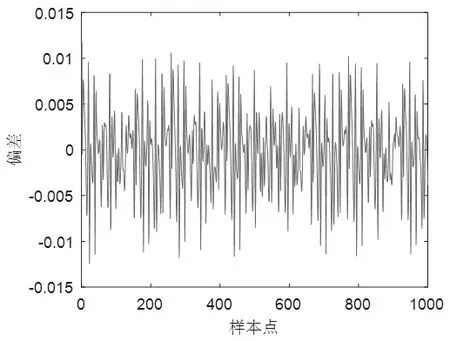
图4 模糊模型与原始输出误差曲线（实例2）Fig.4 Fuzzy model and original output error curve (Example 2)