基于EWT-PSO-Elman耦合模型在径流预测中的应用
2022-09-29莫崇勋邓云阮俞理雷兴碧麻荣永孙桂凯
莫崇勋, 邓云, 阮俞理*, 雷兴碧, 麻荣永, 孙桂凯
(1.广西大学土木建筑工程学院, 南宁 530004; 2.广西大学工程防灾与结构安全教育部重点实验室, 南宁 530004; 3.广西大学广西防灾减灾与工程安全重点实验室, 南宁 530004)
由于气候同人类活动等因素的影响,径流序列常常表现出非平稳性、非线性特征,一般的回归分析等预测方法较难取得理想的预测结果,因此需要不断探索并应用新的方法以提高对径流预测的准确性。Elman神经网络[1]具有较强计算能力和时变适应能力,较经典非线性模型BP(back propagation)神经网络,具备更好的全局稳定性,且拥有短期记忆功能等优点。但是,现有Elman算法是以梯度下降法为基准,易导致训练速度慢和陷入极小点,致使神经网络训练容易陷入局部最优。目前遗传算法[2]、粒子群算法[3]等已试用于Elman关键参数优化。李志新等[4]采用GA算法优化Elman参数以解决神经网络静态性及训练算法易陷入局部极值缺陷,构建了GA-Elman预测模型,结果显示预测平均相对误差从7.07%降低到5.29%,预测模型性能得到明显改善。但是,遗传算法存在参数设置复杂、易过早收敛、效率低等问题。其中,粒子群算法是一种基于迭代的优化算法,无较多参数,容易实现,在一些工程方面已被证明优于遗传算法[5]。但由于径流序列复杂性和多周期的特征,仅仅对优化 Elman 参数难以达到较好的效果,因此需要寻求方法挖掘序列中的规律成分和关键成分,使得预测精度能进一步提高。
近年来,预测模型的耦合越来越受到水文研究者的关注,以分解算法为基础,对数据进行预处理降低序列非平稳性来达到提高模型预测精度的目的。如经验小波分解(empirical mode decomposition, EMD)[6]、集合经验模态分解(ensemble empirical mode decomposition, EEMD)[7]方法常被应用于信号分解中,但其存在模态混叠、端点效应等特征,经验小波变换算法(empirical wavelet transform,EWT)[8]具有良好理论基础,且分解模态少,使得分解后序列更加平稳,减少混合建模的预测误差。张先起等[9]基于小波分解与Elman网络的优点,将其构建成组合模型小波分解-Elman,并与CEEMD-Elman 模型、BP模型作对比,并在地下水埋深的预测耦合模型进行验证,结果表明小波分解-Elman模型的精度最高。鉴于此,现通过对径流序列进行模态分解,进而建立一种基于EWT、PSO和Elman神经网络的耦合月径流预测模型(EWT-PSO-Elman),并将模型应用于西南典型岩溶区澄碧河流域坝首站月径流预测中,验证其预测精度和适应性,以期为非平稳、预测提供新思路。
1 基于神经网络的EWT-PSO-Elman月径流预测模型
1.1 EWT算法
经验小波变换(EWT)通过在频谱上的分割,从而在各频带上构建适合的正交小波滤波器组,并且结合了 EMD 的自适应优点,把信号分解成多个具有紧凑支撑特性的频率特征信息相异的分量[10]。计算步骤如下。
步骤1通过使用最小二乘法处理原始信号,分离出其中的趋势项,再进行去除。
步骤2对输入信号频谱进行傅里叶变换,归一化至[0,π]。
步骤3设置模态个数M,并且计算其中两个具有连续性的局部极大值的中间频率,并将计算值作为频谱划分边界ωn(n=1,2,…,M-1)。
步骤4根据各频谱分割后的状态分别构建尺度函数φn(ω)和小波函数ψn(ω);再次使用傅里叶变换计算F(ω)×φn(ω)和F(ω)×ψn(ω),最终得到各分量的时域表达式。
1.2 PSO算法
粒子群算法[11](particle swarm optimization,PSO)是美国的Kennedy和Eberhart受鸟群行为所启迪并于1995年提出的。粒子群算法是一种全局优化算法,其基于鸟群的觅食行为,通过合作和信息传递寻找最优解,其设置参数少,收敛速度快,有较强的全局寻优能力。
Elman神经网络中网络连接权重、阈值和隐含层神经元数量会直接影响Elman模型预测精度,通过PSO算法迭代寻找最优的权重、阈值和隐含层个数,算法原理如下。
首先初始化随机生成一群粒子,迭代过程中,各粒子由适应度值找到个体历史最优和群体历史最优解,根据式(1)和式(2)进而更新自己速度和位置。

(1)
xi(t+1)=xi(t)+φvi(t+1)
(2)

1.3 Elman神经网络
在局部回归网络中,Elman神经网络是较为典型的一种。它是一种具有极强的计算能力的前向神经网络,能够组合局部反馈与局部记忆单元。Elman 神经网络由输入、隐含、输出和承接层4层结构组合而成,相比于一般静态神经网络,具有逼近速度快、动态特性好等特点[12]。该模型的计算公式为

(3)

(4)

(5)
式中:

1.4 PSO-Elman算法
该优化算法的核心思想是通过PSO算法优化Elman网络的权值和阈值,可改善Elman神经网络的预测效果。
具体步骤如下。
步骤1将粒子群参数和Elman神经网络进行初始化。Elman神经网络的初始化主要包括确定输入层、隐含层和输出层的层数。粒子群参数的初始化主要有粒子位置和粒子速度的范围限定,层数、学习因子、迭代次数和种群规模。
步骤2确定粒子评价函数。种群中粒子适应度函数表示为

(6)
式(6)中:n为种群规模;yi为实际输出值;Yi为样本输出值。
步骤3据式(6)计算各粒子适应度值并排序,进一步创建粒子群的规则树结构。
步骤4时刻更新各粒子位置,进一步寻求各粒子的全局和局部最优位置。
步骤5据式(2)中确定的粒子评价函数更新粒子位置和速度。
步骤6一旦达到迭代结束条件就结束,否则将继续步骤三进行再次迭代。
步骤7将获取的最优结果对Elman神经网络权值和阈值进行赋值,Elman模型训练后,输出最优预测解。
1.5 基于EWT-PSO-Elman的组合预测模型
EWT方法继承EMD和小波分析方法的各自优点。PSO算法属于智能优化算法,属于进化算法之一,能科学处理约束全局的优化问题。Elman神经网络具有逼近速度快,动态特性好的优点。综合以上两种算法的优点,并与EWT结合对径流序列进行预测,构建了EWT-PSO-Elman耦合预测模型。
基于EWT-PSO-Elman耦合模型的预测步骤如下。
步骤1采用EWT对实例月径流数据先进行预处理,则得到几种不同特征的经验模态分量IMF,每个分量具有不同的频率和周期,分别对应原始信号的不同特征。
步骤2进行各IMF的PSO-Elman时序预测。据各不相同频率模态分量{IMF1,IMF2,…,IMFn}对应构建PSO-Elman模型,完成各分量预测后,对结果求和。
步骤3对预测结果进行计算。
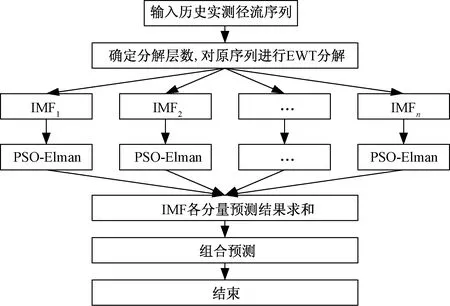
图1 EWT-PSO-Elman耦合模型预测流程图Fig.1 EWT-PSO-Elman coupled model prediction flow chart
EWT-PSO-Elman耦合预测模型流程如图1所示。
1.6 模型评价和优选
为评价预测模型的预测性能,参考《水文情报预报规范》[13],选取能够对两组非线性相关数据的拟合程度进行评价而被广泛应用于水文模型性能评估中的纳什效率系数(NSE)、均方根误差(RMSE)和平均相对误差绝对值(MAPE)共3种评价指标。

(7)

(8)

(9)

2 应用
2.1 数据来源
澄碧河流域位于百色市凌云县北部的青龙山,平均海拔650 m,属西江水系。流域总面积为 2 087 km2,其中岩溶区面积占总面积53.7%,干流河长151 km。该岩溶区是中国南方典型的岩溶区之一,具有高峰丛状洼地的特征,属喀斯特地貌。水库坝址以上集雨面积2 000 km2,约占整个流域集雨面积的95.8%,年平均降水量为1 560 mm,汛期降水约占全年降水的87%,多年平均流量约为37.8% m3/s,且流域属于亚热带季风气候,雨热同季,夏长冬短。以澄碧河水库坝首站为例,搜集选取坝首站1979—2019年共492个月的历史径流数据作为EWT-PSO-Elman径流预测模型数据集(图2)进行研究,并将训练集与测试集比例划分为8∶2,即前394个月作为模型训练期,后98个月作为检验期。流域位置图和示意图如图3所示。

图2 坝首站月径流序列Fig.2 Monthly runoff series at the dam head station
2.2 参数设置
在EWT-PSO-Elman模型对PSO的参数设置中,参考已有研究成果基础上[14],经过反复测试和结合数据特征,设置种群规模为10;初始化种群粒子位置和速度设置在[0,1];学习因子,即每个粒子所需要的加速度参数,本文设定c1=2,c2=2;最大迭代次数设置为50;惯性权重,一般惯性权重的设置区间为0.3~0.9,本文设定为0.9。其中Elman的输入层节点数设为1,以训练目标最小误差为目标进行隐含层层数动态寻优,对比测试后设定隐含层层数为10,隐含层节点数为11,训练次数设为 1 000,输出层节点数设为1,学习速率设为0.01,训练目标最小误差设为0.000 01。
2.3 预测及对比分析
2.3.1 EWT分解
在采用小波方法进行时间序列分析时,小波分解层数对结果有较大影响,其中,分解层数根据杜文辽等[14]提出的小波滤波分解层数的自适应方法确定,经反复测试,当进行4层分解时,模型性能能够达到最佳,其每个IMF分量代表一组特征尺度(频率),因此EWT分解实际上是将原始数据序列分解成不同尺度的叠加,各个IMF分量既可以是非线性的,也可以是线性的,而且各个IMF分量都有不同的物理背景相呼应。它不仅包含了原始序列的全部信息,而且突出了原始序列的不同特征,使得模型能够更准确地学习径流序列的周期性和规律性特征。小波分析具有强大的多尺度分辨功能,能识别水文序列的各种频率成分,EWT分解如图4所示。
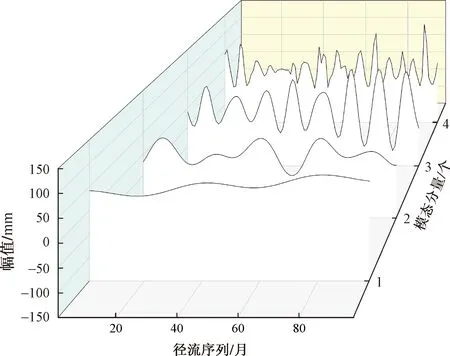
图4 EWT分解结果Fig.4 EWT decomposition results
各子序列表现出该径流序列的振幅变化和频率变化,其中,IMF1分量相较其余分量,频率最小,振幅最小,波长最长,波动情况最为平缓,IMF2~IMF4频率逐渐增大,波长随之变短,振幅逐渐变大,且表现一定的周期性,其中IMF1的波动范围为 30~75,IMF2的波动范围为-50~38,IMF3的波动范围为-110~98,IMF4的波动范围为-55~124。
2.3.2 预测结果分析
EWT-PSO-Elman、EWT-PSO-BP、PSO-Elman、PSO-BP、Elman和BP模型月预测结果如图5,预测效果如表1所示。
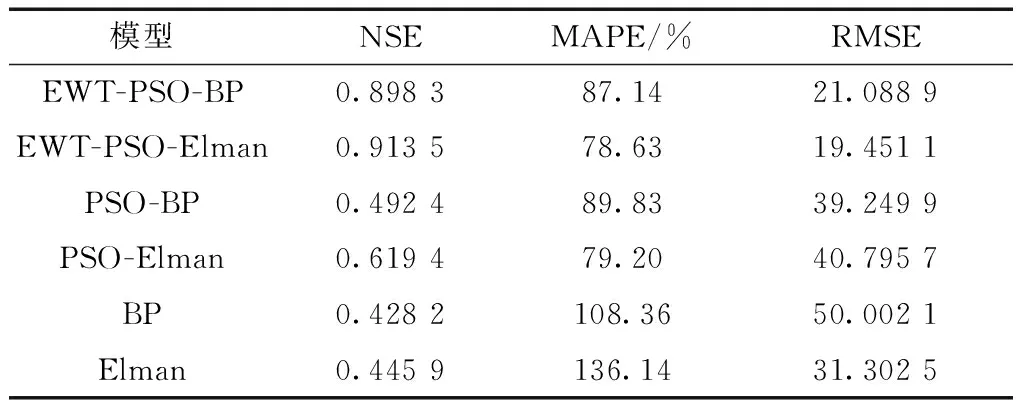
表1 各模型在验证集上的预测效果
由图5可知:①单一BP和Elman模型预测效果较差,只能反映出序列的大概趋势,预测值与实测值的结果相差较大,单一BP和Elman模型对月径流深峰值的预测效果较差,预测值与实测值相差约为54%、47%;②PSO优化的Elman模型较PSO优化的BP模型好,这取决于Elman模型的收敛速度快,训练准确度和分类精度更高,但对月径流深峰值的影响不明显;③EWT-PSO-Elman耦合模型的预测精度最高,预测径流序列趋势与原序列趋势的一致性最高,无较大差别,与其他模型相比,峰值优化明显,预测值与实测值相差约4%,有效地降低了序列非平稳和非线性带来的影响,取得较好的预测效果。
为进一步探索各模型的预测精度情况,对各评价指标进行分析,如表1所示。
(1)从参数优化前后性能来看:坝首站的PSO-Elman模型较Elman模型的NSE提高了约38.9%,MAPE减少了约41.8%,坝首站的PSO-BP模型较BP模型的NSE提高了15%,MAPE和RMSE分别减少约17.1%、21.5%。
(2)从小波分解前后性能来看:坝首站的EWT-PSO-Elman模型较PSO-Elman模型的NSE提高了47.5%,MAPE和RMSE分别减少约0.7%,52.3%,EWT-PSO-Elman模型较Elman模型的NSE提高了约 104.9%,MAPE和RMSE分别减少约42.2%、37.9%。坝首站的EWT-PSO-BP模型较PSO-Elman模型的NSE提高了82.4%,MAPE和RMSE分别减少约3%、46.2%,EWT-PSO-BP模型较BP模型的NSE值提高了109.8%,MAPE和RMSE分别减少约19.6%、58%。

图5 月径流模拟结果图Fig.5 Monthly runoff simulation results
(3)从同一模型预测效果对比来看:在预测精度上,EWT-PSO-Elman>PSO-Elman>Elman,EWT-PSO-BP>PSO-BP>BP。
(4)从整体上看:EWT-PSO-Elman模型的预测精度最高,大于EWT-PSO-BP模型,表明在PSO有效优化Elman权值和阈值,EWT有效处理数据非平稳性和非线性特征的结合上能有效提高Elman预测精度,将EWT-PSO-Elman模型应用于径流预测是可行的。
3 结论
通过构建EWT-PSO-Elman神经网络模型,应用于月径流深预测中并分析验证,得到如下结论。
(1)所构造的耦合模型的预测精度远大于单一模型,通过“分解-预测-重构”模式可有效提高预测精度。
(2)对比分析结果显示,本文提出的EWT-PSO-Elman模型优于EWT-PSO-BP模型、PSO-Elman模型和PSO-BP模型,可为径流预测工作提高一定的参考。
(3)本文所提的EWT-PSO-Elman耦合模型能提高径流预测精度。但仅应用于月径流中,今后可探讨不同时间尺度的适用性。
