求解多起点多旅行商问题的K-means聚类信息传播算法
2022-09-29程亚南王晓峰刘凇佐莫淳惠
程亚南, 王晓峰,2*, 刘凇佐, 莫淳惠
( 1. 北方民族大学计算机科学与工程学院, 银川 750021; 2. 北方民族大学,图像图形智能处理国家民委重点实验室, 银川 750021 )
旅行商问题(traveling salesman problem,TSP)作为NP难问题,近年来研究的热度只增不减,多旅行商问题(multiple traveling salesman problem, MTSP)是其扩展问题。相对于传统的TSP问题来说,MTSP更符合现实社会的复杂条件,在现实生活中应用更加广泛,在无人机路径规划、不同社区快递配送、调度等实际问题中比较贴合。相较于TSP问题,同样作为NP难问题的MTSP的求解难度在于求解的过程中需要进行分组优化,组内进行TSP的遍历。由于MTSP贴合实际情况的特性,近年来在学术界关注度较高,所以有效地求解MTSP的方法有助于解决现实生活中的问题。但是目前对于求解MTSP的算法研究还不够深入。在以往的研究中大致可以分为两类:精确算法和启发式算法。分支限界是现阶段为止最为精确的算法,可以用来求解TSP和小规模的对称型MTSP问题,精确算法的发展虽然解决了一些问题,但是其本身严格的数学定义,在求解时受到很大的限制,随着城市规模的增大,MTSP问题的维度会迅速增加,精确算法求解的难度逐渐提升,难以在合理的时间找到最优解。基于此,启发式算法越来越受到研究者的青睐。文献[1]提出一种改进分组遗传算法,设计了新的分组编码构造了一种快速交叉算子,同时,设计了一种新的局部交叉算子用来提高算法的求解精度。文献[2]提出一种新的求解MTSP的断点算子-初等断点算子,主要是通过初等矩阵运算来生成MTSP的解空间。文献[3]利用模糊C均值聚类按照城市隶属度划分类别,用单亲遗传算法求解分类的旅行商问题。近年来,MTSP问题引起众多研究人员的关注,一些新的启发式算法被改进解决MTSP问题。文献[4]利用改进的人工蜂群算法(artificial bee colony,ABC)与入侵杂草算法(invasive weed algorithm, IWA)相结合求解MTSP问题。文献[4]针对MMTSP问题,提出了一种改进的两部分狼群搜索算法(modified two-part wolf pack search, MTWPS),算法的全局性得到了提高。
上述启发式算法在局部搜索与全局搜索的平衡和求解质量上存在不足。现主要针对多旅行商问题中的多起点进行研究,提出了一种基于K-means聚类方法的信息传播算法来求解。信息传播算法的思想起源于统计物理学,信息传播算法可以解决多种图模型上的概率计算问题,在消息传播的过程是并行实现的,时间复杂度得到了降低,所以选择信息传播算法进行分组后的旅行商问题进行求解。
1 基本知识
1.1 多旅行商问题
MTSP[5]是传统TSP问题的一种扩展,与传统的TSP不同之处在于,MTSP是m个推销员访问n个城市(n>m),保证每个城市只访问一次。目标依旧是访问距离最短也就是m个旅行商旅行的距离之和最小。多旅行商问题会根据不同的起点城市和每个旅行商访问的城市个数分为不同的类型。现主要针对多起点闭合路线的MTSP问题。m个旅行商从不同的城市出发,访问一定数量的城市后返回出发城市,要求每个城市只能被一个旅行商访问一次。

(1)

1.2 K-means聚类方法
K-means[6]属于无监督学习的聚类算法,算法本身比较简单,对于给定的数据集,算法按照样本点之间的距离大小进行划分,划分结果是K个簇也可称为k类,同簇之间相似度较高,簇与簇之间相似度较低。算法迭代终止的条件是类簇中心点变化较少或者达到预先设定的迭代次数。基本原理是给定的数据集样本D={x1,x2,…,xm},初始中心点,从D中随机选择k个样本作为初始均值向量,计算样本与均值之间的距离,根据距离最近均值向量确定的簇标记,重新计算更新均值向量,均值向量未更新则输出簇划分C={C1,C2,…,CK}。
算法的基本步骤如下。
步骤1选定聚类的个数k,随机初始化k个中心点。
步骤2针对数据集中的每个样本点,找到距离其最近的中心点,按照样本点距离每个中心点的距离选择聚类。
步骤3聚类前后样本点不再发生变化,聚类达到稳态,则算法终止,否则进入步骤4。
步骤4对步骤3聚类后的类别进行中心点的更新,转至步骤3。
将聚类算法应用到旅行商问题上,假设城市个数n=9,旅行商个数m=3,9个城市进行编号聚类设置k=3,这里每一个旅行商访问的城市数目并不均等,就可得到{{1,3,8,1}{2,4,7,2}{5,6,9,5}} 3组数目不等的城市组合,在第二阶段对每一组按照传统的旅行商问题进行遍历排序就可以。
1.3 因子图
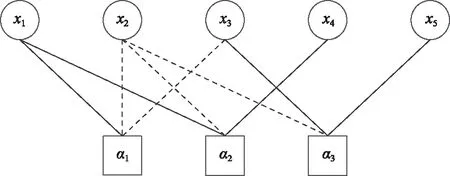
因子图[7]是一个特殊的二分图,代表由许多变量组成的全局函数分解成局部函数的图示。信息传播算法以因子图为工具,可以直观地表现一个多种约束条件的复杂问题。如函数p(x)可以分解成fA、fB、fC、fD、fE5个局部函数的乘积,构造对应关系为式(2)的因子图如图1所示。
p(x1,x2,x3,x4,x5)=fA(x1,x2,x3)fB(x2)·
fC(x3,x4,x5)fD(x4)fE(x5)
(2)

例如,对于一个CNF公式:


(3)
其因子图如图2所示。

图1 因子图实例Fig.1 Example of factor graph
α1=(x1∨x2∨x3),α2=(x1∨x2∨x4), α3=(x2∨x3∨x5) 图2 因子图实例Fig.2 Example of factor graph
1.4 最小和信息传播算法
1988年人工智能领域著名学者Pearl提出了置信传播(belief propagation, BP)算法,BP算法把全局的概率推理过程转变为局部变量间的消息传递,从而降低了推理的复杂度。因为BP算法的优点,自提出起,就受到了国际上众多学者的关注,掀起了研究的热潮。
置信传播算法[8]的特征是基于因子图上的边传递消息,当这种消息传递达到一种稳态时,可计算因子图上节点取值的边际概率,从而以高概率地确定变元的某种取值。研究结果表明,信息传播算法求解组合优化问题性能较好。当前,置信传播算法除了以“和积”的形式传递信息,近年来出现由和积算法简化的最小和算法,目前国内外主要是针对和积算法进行研究。
最小和信息传播算法[9]是一个信息逐步迭代的过程,在因子图的边 (i,α)上信息随着过程的迭代进行更新。μi→α(di)表示由变量节点发出给因子节点的信息;代表变量i取值为di的信息;μα→i(di)表示由因子节点发给变量节点的信息。信息迭代方程为
(4)
(5)
式中:V(i)为与i相连接的因子节点集合;V(i)a为不包含a的因子节点集合;V(a) 为与a相连接的变量节点集合;V(a)i为不包含i的变量节点集合;fa(dj)是对应问题的描述函数,也称为势函数。当BP收敛时,边际信念表示为
(6)
2 求解MMTSP的K-means聚类信息传播算法
2.1 旅行商问题的线性规划方程
旅行商问题可以用非负赋权无向图G(V,E)表示,旅行商问题的约束条件为每一个城市只能一条边进,一条边出,即旅行商问题的线性规划方程为
minimizewTx
xe∈[0,1]|E|
(7)
式(7)中:图中各边的权重集合为w=(w1,w2,…,wm),边的标签属性集合为x=(x1,x2,…,xm)T,标签x1=1,该边加入回路,反之,不加入回路;δ(v)是顶点v所连接的边;xe是顶点v加入回路边数量;|E|是边数目的模。
2.2 旅行商问题的因子图
图结构用G(V,E)表示,i和j两个节点之间的距离表示为wi:j,V={v1,v2,…,vn}为节点集合,节点之间存在边相连则(i:j)=1。令d={d1,d2,…,dM}∈{0,1}M是一组M维二进制变量,其中M=|E|。如果节点i和节点j所在的边在TSP问题的可行解中则di:j赋值为1。
根据TSP问题的特性定义两种条件约束。
(1)成本约束:代表因子图上边的成本,当i和j两个节点存在边,信息为非负距离,反之为0。
(8)
(2)势函数:确保每个结点刚好都与其他两个结点连接。
(9)
这里用小规模的旅行商问题给出无向图转换因子图的示例,如图3所示,图3(a)为四个城市的简单无向图,城市分别用a、b、c、d表示,城市之间的权重用无向边上的数字表示。边上的数字代表城市之间的权重,图3(b)中变量节点为城市之间的边构成,因子节点为城市和约束条件(势函数),其中白框和黑框分别表示城市和约束条件。

图3 四个城市的无向图示例Fig.3 Example factor diagrams for four cities
2.3 旅行商问题的算法优化
文献[10]针对消息传递的复杂性,提出简化信息的方法。根据TSP的特性, 当di:1=1时,表示节点i和节点j的边选入路径,反之则不选入。令min[k]A表示集合A中第k个最小值,将式(5)进行重写得到消息的更新公式为
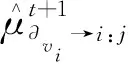
(10)
在BP算法迭代过程中,消息基于因子图进行传递,会产生消息震荡,进而影响算法的收敛速度,动态阻尼[11]是将最近两次的迭代信息加和求取平均值,经处理后提高BP算法信息更新的收敛速度。动态阻尼的公式为
(11)
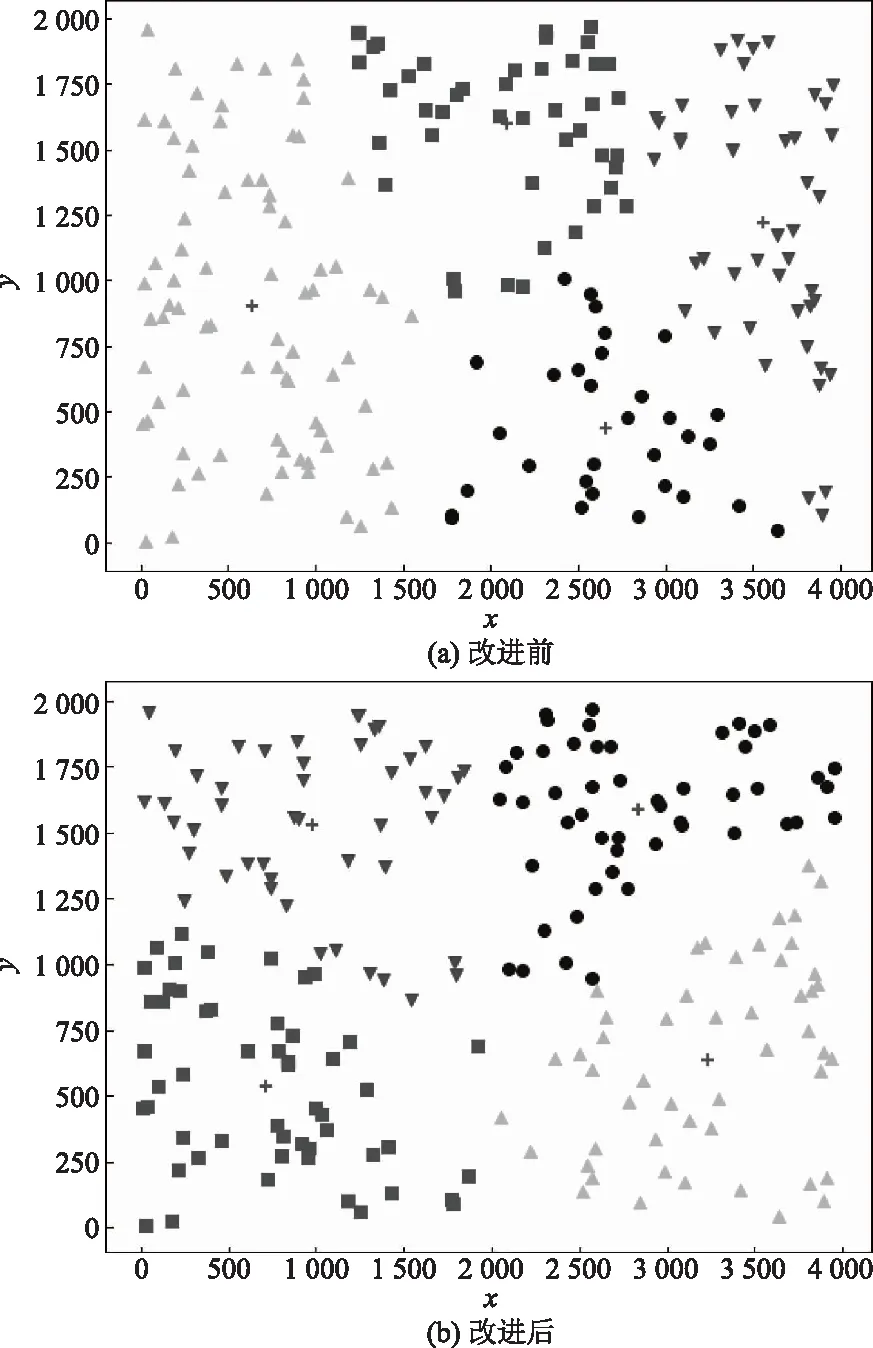
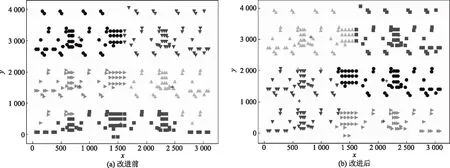
2.4 模拟退火算子
模拟退火的出发点是在固体退火的过程中和组合优化算法的求解是类似的,作为一种随机迭代思想是在搜索过程中进行随机搜索,具有突变性质,解决容易陷入局部最优的缺陷,模拟退火算子具有跳出局部最优的能力,全局搜索能力较强,能够有效求解旅行商问题。
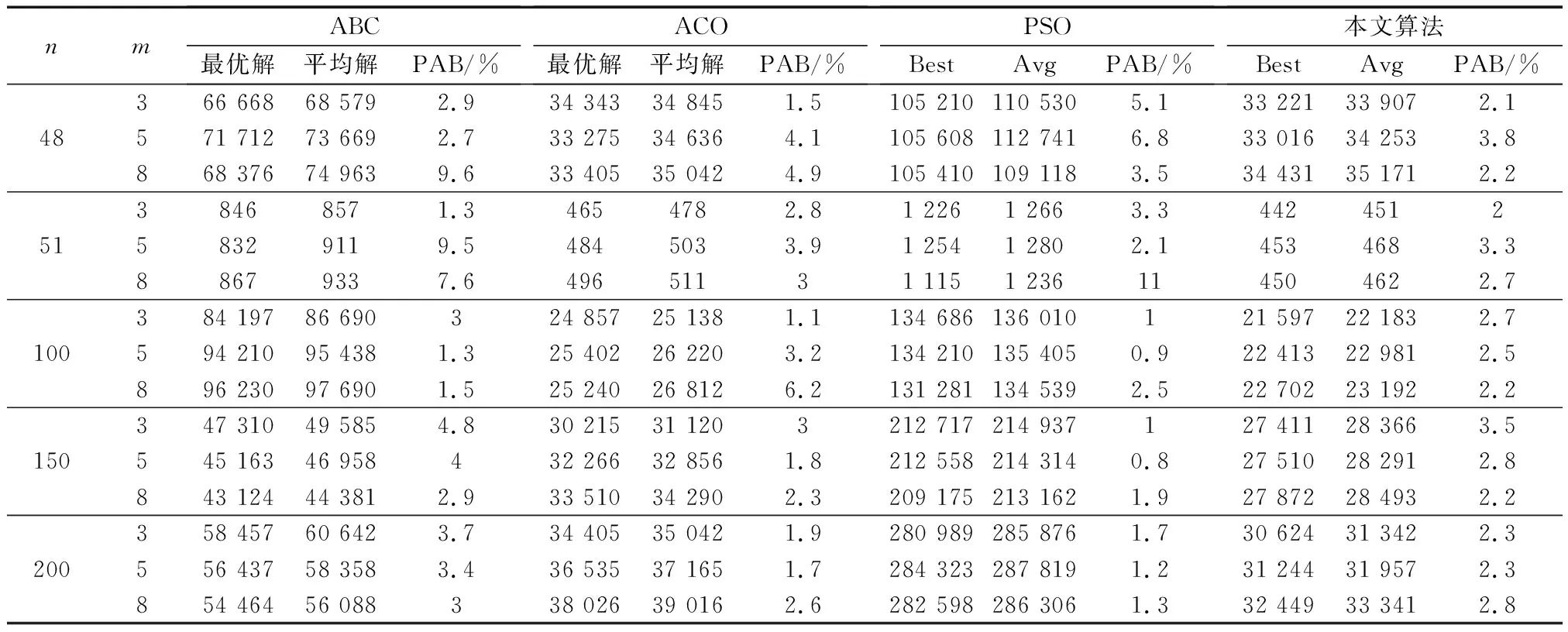
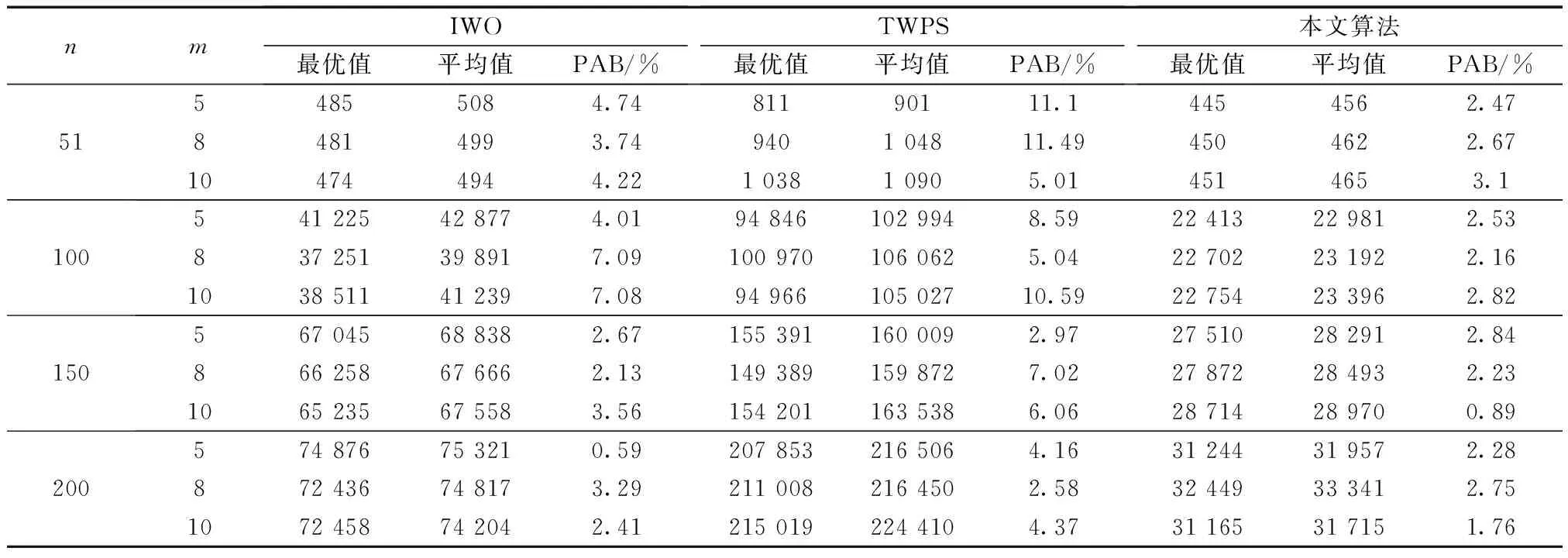
其中模拟退火算子是以一定的概率接受新的解,当在温度T时,从当前解curr改变为新解new;若curr 局部搜索(local search, LS)的过程中采用一定概率选择交换、逆序两种操作,在信息传播算法全局迭代之后采用交换、逆序进行局部搜索,便于找到最好的解。 2.5.1 交换操作及示例 交换操作是在原始解中任意选择两个城市进行交换,如图4所示,左侧是原始路径经过选择城市3和城市7,变换后城市序列如右侧所示。 2.5.2 逆序操作及示例 逆序操作和交换操作一样同样任意选取两个城市,将以两个城市为首尾的城市逐一逆序输出,如图5所示,左侧为原始路径,右侧为经过逆序操作的路径图。 图4 交换操作Fig.4 Exchange operation 图5 逆序操作Fig.5 Reverse order operation 时间复杂度为O(n3),算法具体步骤如下。 算法1:求解旅行商问题的信息传播算法输入: 图G=(V,E),加权邻接矩阵A,最大迭代Tmax,阈值εmax输出:巡视中路径Tour⊂E1 构造初始化因子图2 初始化势函数信息^μi:j→∂vi←0∀i∈V,j∈∂vi 3 初始化^φi:j←wi:j∀(i:j)∈E 4 While True:4.1 ε←0,T←04.2 Whileε<εmax and T K-means在聚类算法思想简单,聚类时间快,但是也存在一些缺点,初始点的随机产生对算法会造成一定影响,其中改进的K-means算法较多,基于K-means++[12]的基础上使用长度为m的独立马尔可夫链在每一次迭代中进行中心采样。随机选择一个中心点,在迭代的过程中通过概率计算进行中心点的更新。 聚类方法的伪代码如下。 算法2:K-means质心选择输入:数据集D,聚类个数K,链长M输出:K个质心的矩阵Cc1←random.choice(D),C←c1For x in D:q(x)←d(x,c1)2/2[∑x'∈Dd(x',c1)2]+1/2DFor i in range(2,K+1):x←random.choice(D,p=q(x)) #根据概率随机选择dx←d(x,ci-1)2For j in range(2,M+1): y←random.choice[D,p=q(y)] dy←d(y,ci-1)2 If d(y)×q(y)>Unif(0,1)×d(x)×q(x): x←y,dx←dy ci←ci-1∪{x}Return C 比较了K-means和改进的K-means++的聚类效果,发现改进后避免了随机化中心点对算法造成的影响。在聚类效果上进行对比,对比效果如图6、图7所示。 在对数据集的处理上,基本的聚类方法,聚类点不均,存在离散点分簇不明,经过多次实验对比,测试改进算法针对旅行商问题分组明朗,不存在异常点,求解距离更短,所以选择改进的K-means++进行MMTSP的分组。 图6 Kroa200分组效果图Fig.6 Kroa200 group renderings 根据不同实验组的解的精度和算法稳定性,实验分析为两个部分。使用TSPLIB中标准数据集作为实验数据进行测试。实验环境为:Python3.7,Inter(R)i7-9750H 2.60 GHz,内存为8 GB的个人计算机(personal computer,PC)进行实验分析。经多次试验总结,交换全局搜索能力强,逆序局部局部搜索能力强,本文算法需要局部搜索优化解,故设置交换概率设为0.4,逆序概率设为0.6。 3.2.1 与经典式启发算法性能对比 在众多的经典启发式算法中选择了人工蜂群算法[13-14](artificial bee colnony,ABC)。粒子群算法[15](particle swarm optimization,PSO)。蚁群算法[16](ant colony optimization,ACO)三种经典算法和本文算法进行实验对比。选择这三种经典算法进行比较,蚁群算法[17]和粒子群算法[18]在处理多旅行商问题效果较好,而人工蜂群算法又是最新应用于多旅行商问题的新算法,表1为对比算法的参数设置,其中参数设置根据文献中对应算法进行设置。 在实验过程中每个旅行商必须访问城市,即单个旅行商访问的城市总和大于1,四种算法每个实例独立运行15次的实验结果如表2所示。 从表2中可知,本文算法和经典的三种算法的比较来看,在所测试数据集上,旅行商的个数分别为3、5、8三种情况下,本文算法得到的结果都比对比算法要好。同时引入对比参数PAB(bercentage average best),PAB是平均解与最优解的差值与最优解的比值,PAB小表示平均解和最优解之差小,波动小表示算法稳定。可以看到本文算法的PAB集中在2左右变化,说明算法在不同测试集的上的性能较为稳定。四种算法PAB变化曲线如图11所示。 图7 Lin318分组效果图Fig.7 Lin318 group renderings 表1 算法参数设置Table 1 Algorithm parameter settings 表2 经典算法效果对比Table 2 Comparison of effects of classical algorithms 从图8中可以看出,与经典的三种算法比较可知,人工蜂群算法和粒子群算法波动过大,算法性能不稳定,本文算法在区间[2,4]波动,算法平均解和最优解之差优于其他三种算法,且幅度较小算法稳定性高。结合表2,本文算法解质量好,且针对不同数据集结果稳定。 图8 四种算法稳定性分析Fig.8 Stability analysis of four algorithms 3.2.2 与近年文献改进的算法实验对比 在近年文献中选取改进效果较好的灰狼优化算法[19]和杂草入侵算法[20-21]与本文算法进行实验结果对比如表3所示。 在和近年文献对比的过程中,旅行商个数m进行了增加,分别对m为5、8、10进行测试,所得到的效果本文算法依旧为最优解,改进的灰狼优化算法与本文求得的结果相差近2倍,杂草入侵算法更是相差更多,关于算法求解稳定性方面,只有n=150、m=10和n=51、m=10产生波动,为了更形象地展示对比算法的稳定性,将得到的结果进行了可视化,图9为PAB的变化曲线。 图9 三种对比算法的稳定性分析Fig.9 Stability analysis of three contrast algorithms 从图9可以明显地看出,本文算法整体的变化曲线较为平缓,PAB小于其他两种算法,平均解和最优解之差小。如表3所示本文算法在三种对比算法中求得最优解的同时,对于每个数据集不同的旅行商个数也较为稳定。 针对算法的性能,选取较有公共数据集a280和lin318进行测试,在n=280、m=10和n=318、m=10时四种对比算法运行10次的结果变化曲线,由于经典的算法在求解过程中与本文算法相差甚大,根据参考文献[19]的数据对比,此处选择近年来最新改进效果较好的算法进行比较,结果图10所示。 从图10中可以清晰地看到,在n=280、m=10的情况下,求解精度方面本文算法是最好的,运行10次折线图波动的幅度较小,算法求解较为稳定。对比算法AC-PGA(ant colony partheno genetic algorithms)在四种算法中求解质量和稳定性都比较差,STASA-2opt求解效果有个别点比较好,但是整体波动的幅度较大,结果具有随机性。加入2opt的STASA算法运行10次的效果较为稳定,但是求解能力不如本文算法。在n=318、m=10情况下,STASA(state transition simulated annealing algorithm)求解的结果相差太大,n=318时求解效果相对于在n=280时大幅降低,旅行商个数不变,城市增加40个,算法性能骤减,该算法不适合求解大规模问题。由此可知,本文算法在求解精度和稳定性方面要优于对比算法。图11分别是不同数据集求得最优路径,分类清晰且无交叉,求解的结果是对比算法中的最优解。 表3 改进算法效果对比Table 3 Comparison of improved algorithm effects 图10 四种算法的效果对比Fig.10 Comparison of the four algorithms 图11 不同数据集的最优路径效果Fig.11 The optimal path renderings of different sets 多旅行商问题具有强大的实用背景和理论价值,提出一种基于改进K-means++聚类的信息传播算法求解多起点的多旅行商问题(MMTSP)。采用两段式方法解决多旅行商问题,采用聚类算法改进的K-means++进行分组,其算法本身简单,聚类时间较快,对大规模的数据集运行效率较高且具有伸缩性,改进的K-means++算法中k值根据旅行商的个数进行确定较为简单。分组之后采用改进的信息传播算法进行优化,信息传播算法在图模型上进行迭代,在解决的过程中利用因子图的特性和BP算法的传播性,随机选择开始城市,在因子图上进行迭代运算。实验表明在城市数目较少的情况下,信息传播算法可以在较少的迭代次数中直接求得最优解。但是随着城市数目的增加,因子图会变的复杂从而影响解决问题的效率,加入局部搜索算法可以很好的解决这一问题。经多数据集测试和多种算法比较,本文算法求得最优解和平均解效果优于其他算法,PAB更小,并且波动区间小算法稳定。但在旅行商问题规模较大时,城市无向图较为复杂,因子图更加庞大,计算量进而增加,在个别旅行商问题上,精度会有略微下降,这是算法的不足之处。如何在问题规模较大时,缩减因子图的规模这将是下一步工作首要解决的问题。2.5 局部搜索操作



3 数值实验及分析
3.1 K-means聚类分组分析

3.2 算法性能测试





4 总结与展望
