细长体亚跨声速超大攻角复杂气动特性研究
2022-09-29王方剑宋玉辉
王方剑,宋玉辉,刘 金,秦 汉,陈 兰
(中国航天空气动力技术研究院,北京 100074)
0 引 言
在机载导弹方面,作为攻防对抗主体的空空导弹,需要比目标飞行器具有更高的机动性和敏捷性,导弹的攻击方式也由尾后追击发展成全向攻击方式。新型空空导弹面对下一代飞机、下一代空空导弹系统等高机动目标,必须具备全向攻击能力。采用大攻角和超大攻角飞行,最大限度利用空气动力实现飞行器飞行轨迹和姿态变化是直接提高机动性和敏捷性的最优手段,由此也带来超大攻角流动分离问题,包括复杂的非定常旋涡、涡脱落、旋涡非对称等流动现象,提高对超大攻角复杂非定常流动及其流动机理的认识显得尤为重要。
早在20世纪50年代,对细长体(锥柱体)分离流动特性的探索就已经开始。20世纪80年代以前,由于缺乏强大的计算软件和先进的风洞试验方法,学者们关注点主要集中在附着流和稳定分离区上。随着技术的发展,一些非定常流动特性被揭示出来。Zeiger等对细长旋成体的流动特性进行流动显示水洞试验,认为在大攻角时,细长体旋成体上的流动可主要分为3种流动形态:第1种流动形态是头尖部附近的产生的较为集中的涡旋;随着流动沿轴向向后发展,流动结构逐渐体现为旋涡脱落流动形态(第2种流动形态),涡脱落方向与旋成体呈一定角度;当流动发展至接近底部时,脱落的旋涡涡轴与旋成体平行,形成第3种流动形态。Degani等的研究表明,其非定常流动主要包括类卡门涡街的低频流动、剪切层失稳引起的高频流动,以及介于以上两种频率之间的旋涡干扰流动。
本文针对细长体在超大攻角下存在的旋涡非定常性、旋涡脱落、旋涡非对称等复杂流动现象,采用基于结构网格的雷诺平均/大涡模拟(Reynold averaged Navier-Stokes/large eddy simulation,RANS/LES)混合数值方法,开展细长体复杂气动非定常特性研究,分析新型导弹在超大攻角下的流动机理,为超大攻角气动设计提供理论支撑。
1 超大攻角数值模拟方法
细长体在较大攻角时能够诱导较为明显的非定常旋涡结构。传统的RANS 模型可以在不苛刻的网格要求下较好地计算附着流和小分离流动,但是对脱体的大尺度分离流的应用一直存在难以克服的困难。其根源在于空间旋涡流场中RANS 涡粘性模型假设导致耗散过大,对旋涡非定常流动带来过冲的阻尼抑制作用。大涡模拟(LES)在模拟湍流的细节和流动分离等方面都有很好的精准度,但其对高雷诺数下物面流动的计算量是当前计算机水平所不能企及的,故其与工程应用还有相当大的距离。近年来兴起的多种RANS-LES 混合方法综合了RANS 方法对近壁附着流刻画和LES 方法对空间大分离模拟的各自优点,其中应用最广泛的是脱体涡模拟(detached eddy simulation,DES)类方法。原始的DES 方法将SST模型的湍动动能输运方程耗散项改写为与网格尺度和湍流长度相关的DES 形式。但该方法存在模型雷诺应力损耗(modeled stress depletion,MSD)问题,进而带来网格诱导分离等非物理问题。因此,本文发展了延迟脱体涡模拟(DDES)方法,通过设置延迟函数,克服了网格加密时可能形成的附面层内LES 启动过早的问题。
因此,本文采用DDES 方法对流动控制方程进行求解,算法设置如下:
1)空间项离散:离散格式为基于守恒律的上游中心格式(monotone upstream-centered schemes for conservation laws,MUSCL)方法插值方法的FDSRoe格式。
2)时间项推进:时间推进格式采用的是隐式LUSGS 方法,保证了较高的计算效率与精度,非定常计算采用双时间步方法,并利用当地时间步长加速收敛。
3)湍流模拟:湍流模拟中采用基于剪切应力运输(shear stress transport,SST)湍流模型的DDES方法。
2 细长体外形与网格
2.1 细长体外形
计算采用的外形如图1,弹身采用的圆柱外形,鸭式舵面为“X”型布局,舵面为梯形翼,弹身头部采用的是类半球型头部设计,导弹质心为/=(0.55,0,0)。坐标设置为轴向后,轴向上。
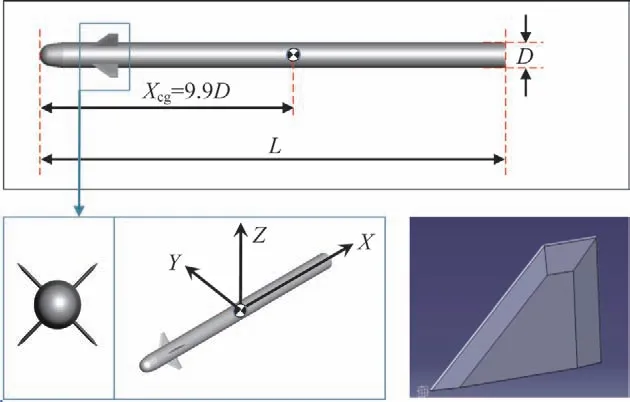
图1 细长体外形Fig.1 Slender body configuration
2.2 数值计算网格
计算网格采用结构网格进行求解,在靠近标模物面处采用O 型网格拓扑,在远离物面处采用H 型网格拓扑,外边界距离的设置以能够满足自由来流条件为判断准则。贴近物面的第一层网格厚度保持~1,以确保边界层的准确模拟。为了能够精确地捕捉细长体外形背风侧的分离涡流动,在模型的法向进行了整体加密,在模型背风侧展向网格进行适当加密(如图3),总网格量为1 500万。
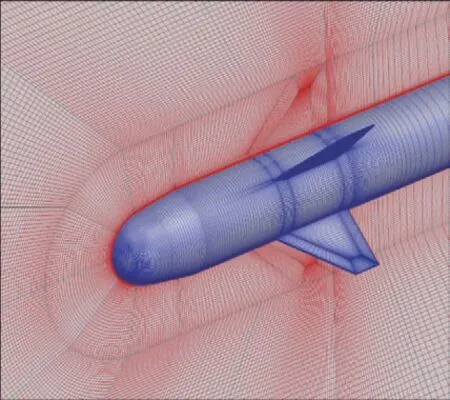
图2 物面分布情况Fig.2 Surface grid

图3 周向网格分布情况Fig.3 Circumferential direction grid
3 超大攻角非定常气动力特性
非定常数值模拟的计算工况参照静态风洞测力试验的试验工况,=0.6、0.8、1.15,=0°~180°,△=15°,共13 个攻角,侧滑角=0°,雷诺数=2.93×10/m。计算采用非定常DDES方法,每个计算物理时间步为1×10,共计算1 200物理时间步。
图4~7 为细长体外形在=0.6 气动力系数随攻角变化情况,图中实线是模型非定常气动力的平均值,阴影部分代表非定常脉动量的量值范围。图4是法向力系数C随攻角变化情况,图中显示,试验模型的非定常脉动量较大的攻角范围是=75°~150°。图5是俯仰力矩系数随攻角变化情况,非定常气动力的脉动影响较大,在某些攻角下(如=120°),其俯仰力矩瞬时值甚至会发生变号的现象。图6~7 是横侧向力矩系数、C随攻角变化情况,在攻角=30°~150°都体现出了较大幅值的非定常特性。从以上图中可以看出,试验模型的气动力在攻角范围45°~165°内具有较为强烈的非定常性,侧向力非定常脉动瞬时值能够达到法向力平均的1/4~1/2。
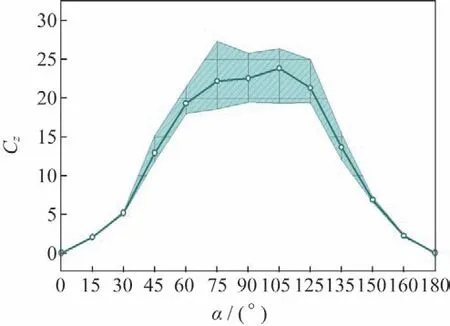
图4 法向力系数随攻角变化(Ma=0.6)Fig.4 Normal force coefficient vs α(Ma=0.6)
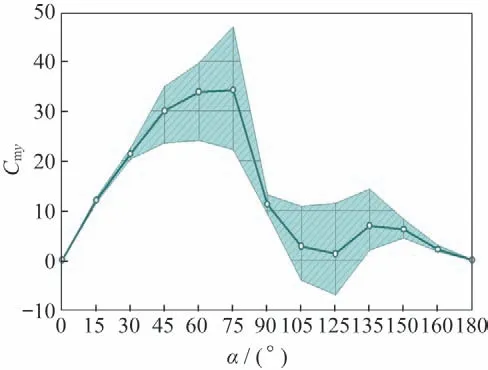
图5 俯仰力矩系数随攻角变化(Ma=0.6)Fig.5 Pitch moment coefficient vs α(Ma=0.6)
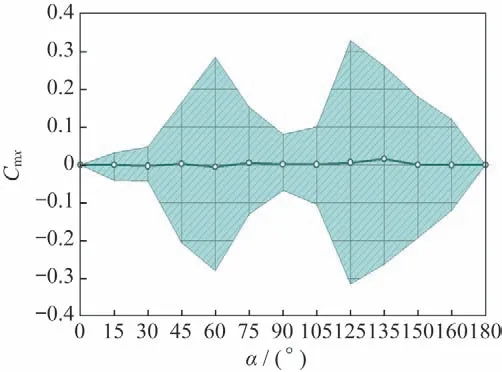
图6 滚转力矩系数随攻角变化(Ma=0.6)Fig.6 Roll moment coefficient vs α(Ma=0.6)
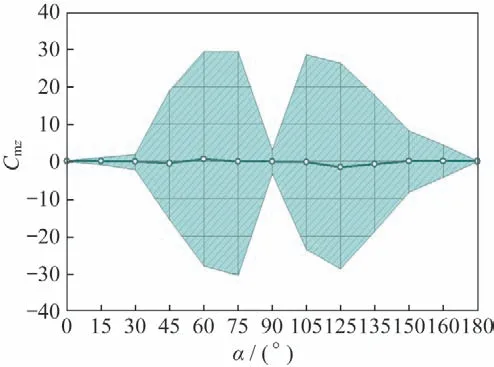
图7 偏航力矩系数随攻角变化(Ma=0.6)Fig.7 Yaw moment coefficient vs α(Ma=0.6)
图8~11 为细长体外形在=0.8 气动力系数随攻角变化情况。图8是法向力系数脉动量随攻角的变化情况,在攻角60°~120°之间体现出了较为明显的非定常脉动特性。图9是俯仰力矩系数脉动量随攻角变化情况,在较小攻角下(0°~30°),非定常脉动量非常小,当攻角达到45°时,非定常脉动量突然增大,在攻角范围45°~135°范围内,其非定常脉动量都体现得较为明显。图10~11 是横航向气动力矩非定常脉动量随攻角变化情况,其非定常脉动量随攻角变化趋势是一致的,即在攻角60°及120°附近脉动量达到最大,在攻角90°附近脉动量有一定程度的减小。
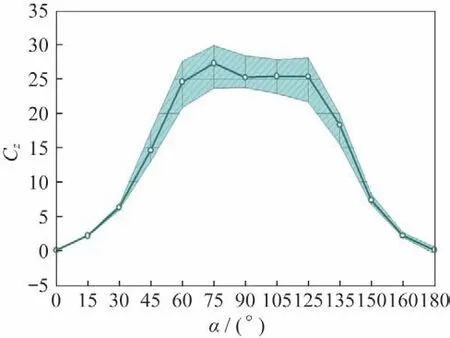
图8 法向力系数随攻角变化(Ma=0.8)Fig.8 Normal force coefficient vs α(Ma=0.8)
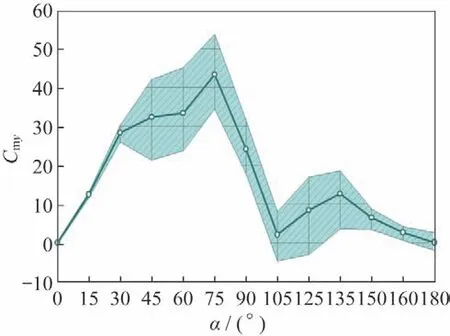
图9 俯仰力矩系数随攻角变化(Ma=0.8)Fig.9 Pitch moment coefficient vs α(Ma=0.8)
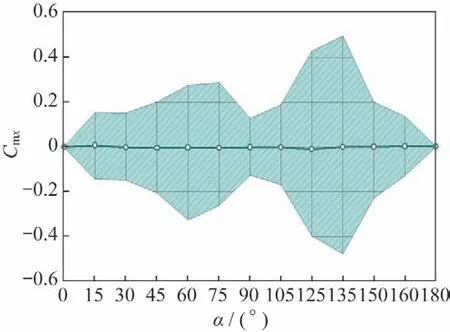
图10 滚转力矩系数随攻角变化(Ma=0.8)Fig.10 Roll moment coefficient vs α(Ma=0.8)
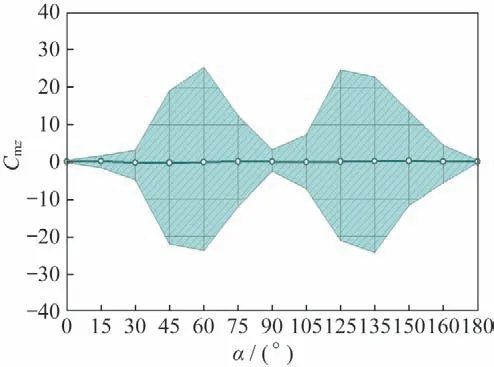
图11 偏航力矩系数随攻角变化(Ma=0.8)Fig.11 Yaw moment coefficient vs α(Ma=0.8)
图12~15 为细长体外形在=1.15 气动力系数随攻角变化情况,图中显示其非定常脉动量与=0.6、0.8 相比有很大程度的减小,反映出了=1.15 下,其非定常流动脉动相对较弱的流动特性。图12为法向力系数脉动量随攻角变化情况,图中显示,其非定常脉动量已较弱,在45°~60°攻角范围内,非定常脉动量相对较大。图13是俯仰力矩系数非定常脉动量随攻角变化情况,图中显示当攻角在45°~60°区间内以及120°附近有相对明显的脉动量。图14~15 是横航向气动力矩脉动量随攻角变化情况,图中显示攻角在45°附近以及165°附近体现出了明显的非定常脉动特性。
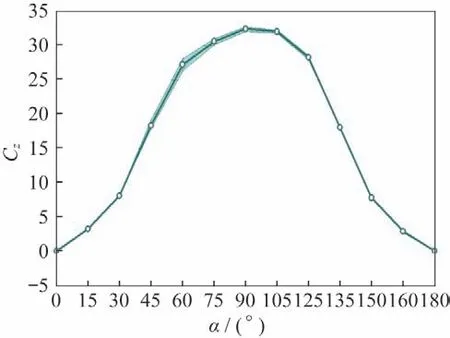
图12 法向力系数随攻角变化(Ma=1.15)Fig.12 Normal force coefficient vs α(Ma=1.15)
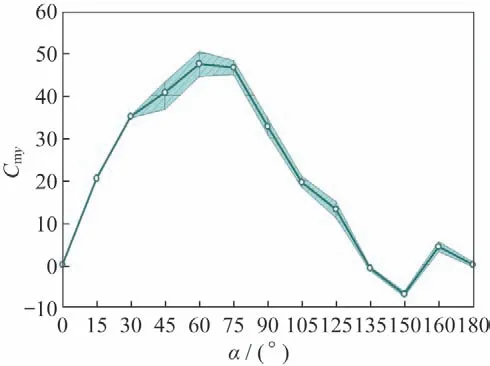
图13 俯仰力矩系数随攻角变化(Ma=1.15)Fig.13 Pitch moment coefficient vs α(Ma=1.15)
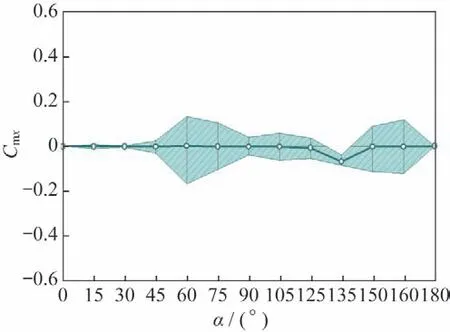
图14 滚转力矩系数随攻角变化(Ma=1.15)Fig.14 Roll moment coefficient vs α(Ma=1.15)
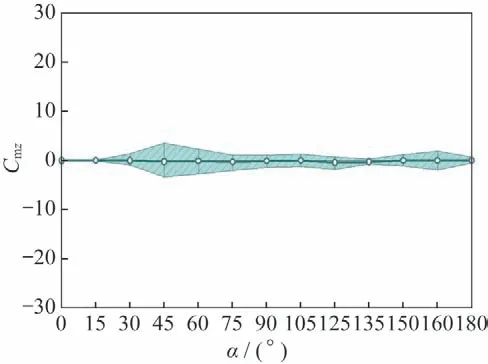
图15 偏航力矩系数随攻角变化(Ma=1.15)Fig.15 Yaw moment coefficient vs α(Ma=1.15)
4 超大攻角非定常频率特性
细长体非定常流动有非常丰富的频率特性。图16中,左侧两张图是=60°时法向力与侧向力系数随时间变化曲线,右侧是其对应的幅值谱。图中显示,法向力与侧向力系数都存在较为强烈的非定常脉动。从幅值谱来看,法向力没有发现明显的主频,但是侧向力系数体现出了明显的主频为820 Hz。由于在不同攻角下纵向气动力系数脉动都体现出了相似的特征,而不同攻角下的横侧向气动力系数则体现了不同的特征,所以本章着重分析横侧向气动力系数的频率特性。
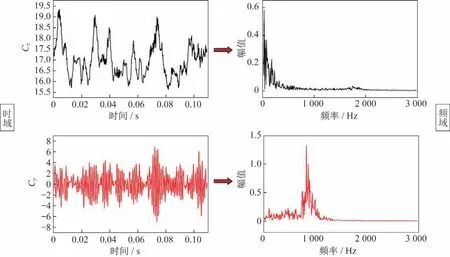
图16 法向力与侧向力系数随时间变化(Ma=0.6,α=60°)Fig.16 Normal force and side force coefficient vs time(Ma=0.6,α=60°)
图17是=0.6,=60°工况下,侧向力系数时间历程计算值与试验数据对比,从图中可以看到计算值与试验值对比较好,计算值稍大。图18是侧向力系数的功率谱密度(power spectral density,PSD)计算值与试验数据对比,图中显示,计算值与试验值获得的侧向力系数主频一致,均为820 Hz。
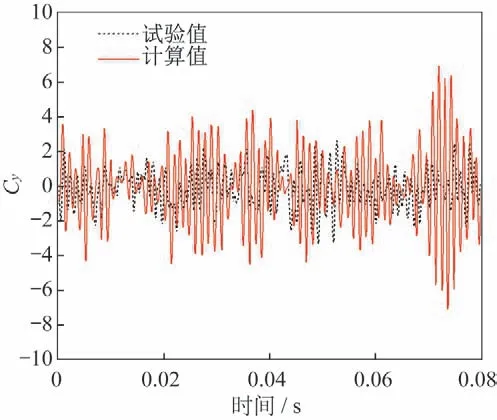
图17 Cy时间历程对比(Ma=0.6,α=60°)Fig.17 Cy vs time(Ma=0.6,α=60°)
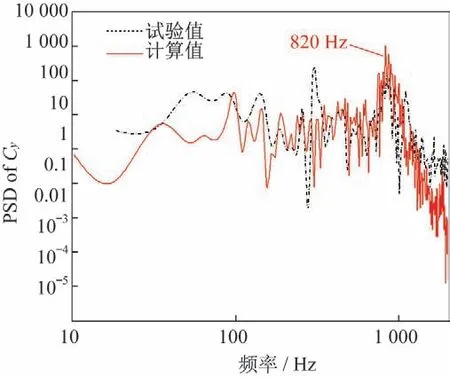
图18 侧向力PSD对比(Ma=0.6,α=60°)Fig.18 Comparison of PSD of Cy(Ma=0.6,α=60°)
图19是=0.6 不同攻角下的侧向力系数随时间变化曲线及其频谱,图中左侧为侧向力系数随时间变化图,右侧为其对应的幅值谱。图中显示,当攻角=30°时,侧向力系数没有体现出明显的主频,主要呈现出一种宽频的特征。当攻角在=60°~150°范围内,侧向力系数均体现出了较为明显的主频。值得注意的是,当攻角=90°时,体现出了两个比较集中的频率,分别为689 Hz 与831 Hz,下文中将对这个问题进行分析。
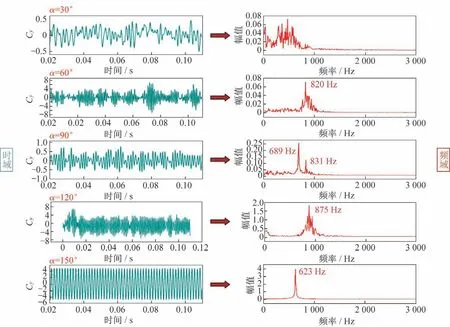
图19 不同攻角下侧向力随时间变化曲线及其频谱(Ma=0.6)Fig.19 Side force coefficient vs time and frequency spectrum at different α(Ma=0.6)
图20是=0.8 时不同攻角下的侧向力系数随时间变化曲线及其频谱。图中显示,在攻角30°工况下,没有体现出明显的主频,其非定常能量主要集中在500~700 Hz 之间。在攻角60°~150°范围内,均体现出了较为集中的主频现象。
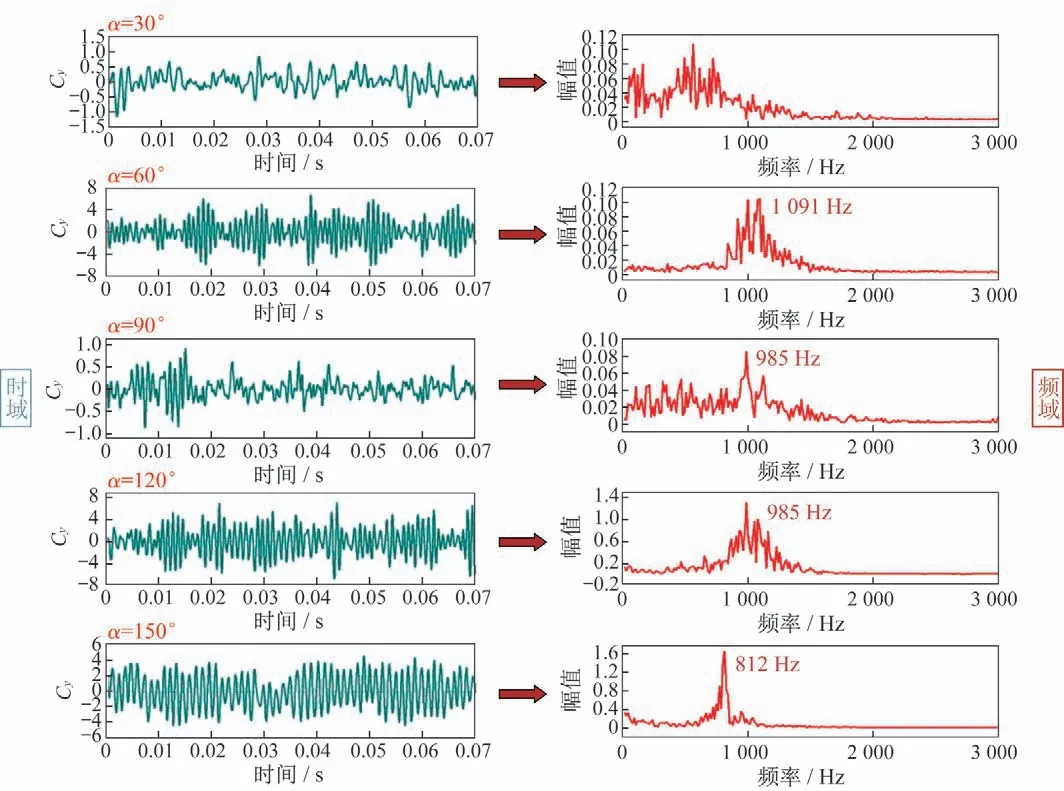
图20 不同攻角下侧向力随时间变化曲线及其频谱(Ma=0.8)Fig.20 Side force coefficient vs time and frequency spectrum at different α(Ma=0.8)
图21是=1.15 时不同攻角下的侧向力系数随时间变化曲线及其频谱,从图中可以看到,与=0.6、0.8 不同的是,其在攻角30°~90°范围内都没有体现出集中的主频特性。攻角为30°时,其非定常能量主要集中在500~800 Hz 范围内;攻角为60°时其非定常脉动能量范围主要集中在1 500 Hz范围内;攻角为90°时,体现出的一种宽频的频率特征,攻角为120°、150°时,体现出了较为集中的主频特性。
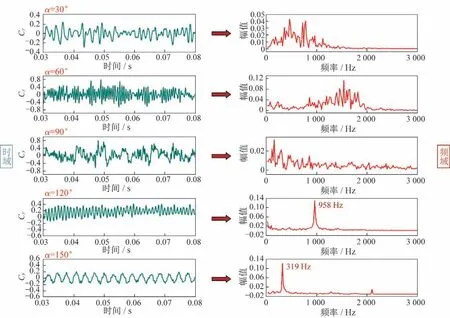
图21 不同攻角下侧向力随时间变化曲线及其频谱(Ma=1.15)Fig.21 Side force coefficient vs time and frequency spectrum at different α(Ma=1.15)
图22是=0.6、0.8、1.15工况下,侧向力系数主频随攻角变化情况。从图中可以看到,随着攻角的增加,其脉动频率主要呈现为先增大后减小的现象。当=0.6时,其主频范围在400~1 000 Hz之间。当=0.8时,其主频范围在500~1 200 Hz之间,=0.8时在各个攻角下的流动主频均比=0.6时大。当=1.15时,只有在45°、120°、150°攻角下流动有明显的主频,其他攻角下并没有发现,其频率范围在300~1 400 Hz。
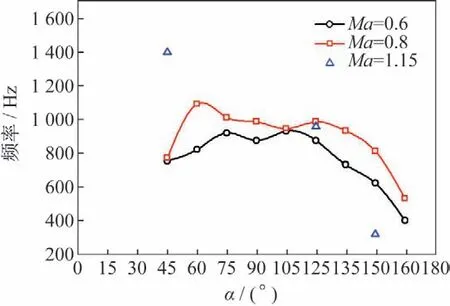
图22 侧向力主频随攻角变化Fig.22 Dominant frequency of Cy vs α
图23是斯特劳哈尔数()随攻角的变化情况。图中斯特劳哈尔数的计算中,速度选取的是横截面的来流速度sin,图中显示,不同攻角下的斯特劳哈尔数量值范围为0.08~0.35 左右。=0.6 与=0.8工况下,其斯特劳哈尔数随攻角变化趋势接近。当攻角在75°~120°区间内,=0.6 所对应的斯特劳哈尔数更大,为0.2 左右;当攻角在135°~165°区间内,两者斯特劳哈尔较为接近,量值在0.25~0.32。=1.15时,攻角150°下斯特劳哈尔较低,只有0.08左右。
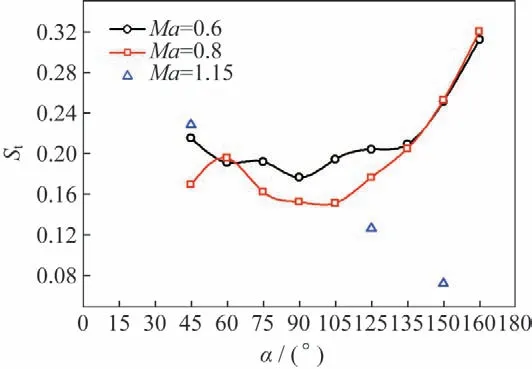
图23 侧向力St随攻角变化Fig.23 St of Cy vs α
为了更进一步地研究非定常频率特性,以=0.6 为例,采用数值模拟方法,在模型的表面布置测压点,其中测压点的分布如图24所示。
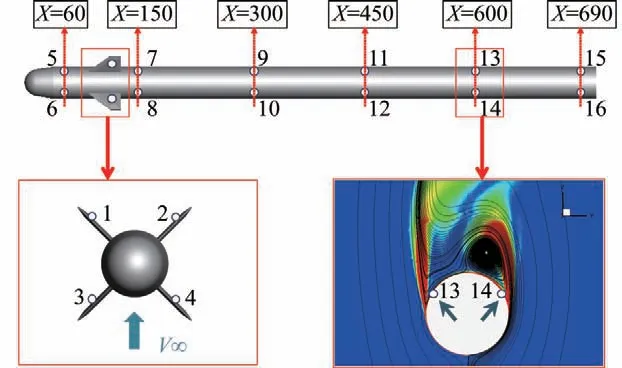
图24 模型测压点布置情况Fig.24 Monitored points location on the surface
图25~27是选取较为典型的3个攻角下的局部压力脉动曲线,每张图中有3张小图,每张小图里上面的曲线为当地压力系数随时间变化的情况,下面的曲线为与其相对应的幅值谱。图25展示的是当攻角=60°时典型测压点的压力脉动情况,图中显示:流动在头部附近体现出了两个频段,一个是0~300 Hz 的较低频段,一个是800 Hz 左右的主频;当流动发展到舵面上时,舵面上的流动没有体现出明显的主频;当流动继续向后发展,其压力脉动慢慢恢复为较为明显的主频,为820 Hz。图26展示的是当攻角=90°时典型测压点的压力脉动情况,图中显示:在模型的头部附近没有看到明显的主频;当流动发展到模型中部时,体现出了明显的主频,为831 Hz;当流动继续向后发展,出现主频降低的现象;在模型接近尾部的地方,流动主频降低为689 Hz。图27所示为攻角=150°时典型测压点的压力脉动情况,可以看出,在模型头部、中部、舵面部分均体现出了很明显的主频,而且其幅值谱非常干净,并且在模型的舵面还体现出了除主频外的多倍频率情况。
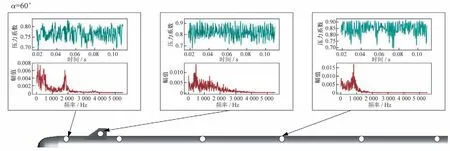
图25 不同测压点压力脉动情况(α=60°)Fig.25 Fluctuating pressure of different points(α=60°)
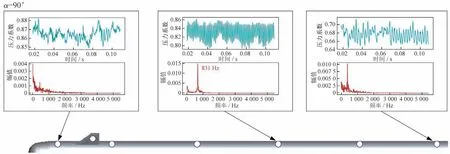
图26 不同测压点压力脉动情况(α=90°)Fig.26 Fluctuating pressure of different points(α=90°)
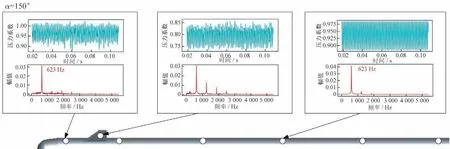
图27 不同测压点压力脉动情况(α=150°)Fig.27 Fluctuating pressure of different points(α=150°)
从非定常频率特性分析中可以发现,试验模型的横侧向气动力(侧向力、偏航力矩、滚转力矩)在攻角45°~165°范围内有比较明显的主频,其范围为400~1 000 Hz;气动力的主频特性主要由旋成体弹身带来,弹翼贡献很小。
5 超大攻角非定常流动特性
超大攻角的非定常气动力以及频率特性的本质是非定常的流动,本章将对细长体的非定常流动进行分析。
图28所示为攻角=60°时的非定常瞬时流动,图中左侧有采用Q 准则进行提取得到的等值面,采用压力来着色,右侧7 张图片是从头部开始不同截面的流动涡量图。从图中可以看到,该外形整体呈现出了非对称旋涡流动,旋涡流动是从前向后逐步发展,当涡位飘得足够高时,其下方又会生成一个新的左侧涡,同时在舵面下游以及尾部下游均出现较为明显的旋涡脱落现象。右侧的涡量图显示:模型流动在头部时(即=0.04),旋涡还在起始发展中,旋涡的非对称现象还不明显;当流动发展到舵面时(=0.15),体现出了较大的分离流动;当流动发展至=0.21 时,由舵面诱导的大分离流动依然存在;随着流动继续沿轴向向后发展,流动开始逐渐演变成类卡门涡街的旋涡流动,出现很明显的非对称旋涡现象,靠近物面的旋涡卷起后逐渐远离物面,同时涡量逐渐减弱,直至脱落。
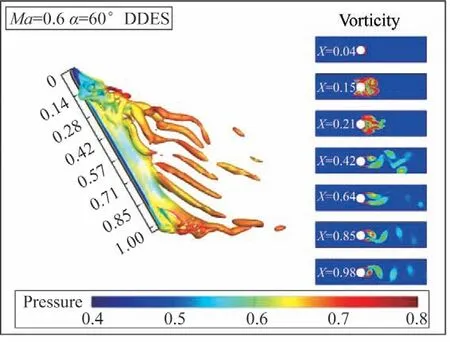
图28 非定常瞬时流动(α=60°)Fig.28 Unsteady transient flow(α=60°)
图29所示为攻角=90°时的非定常瞬时流动,图中显示:模型流动在头部(=0.04)时,已经体现出了大分离、旋涡脱落等现象;当流动发展至=0.42 时,其流动特性演变为类卡门涡街流动,同时随着时间的变化进行左右切换。与攻角=60°不同的是,攻角=90°时旋涡涡位较高,并且涡量较低,这主要是由于在此攻角下轴向流动速度很低。值得注意的是,当流动发展至模型尾部(=0.98)时,旋涡的非对称性减弱,近似于对称涡,并且没有脱落。这是由于流动绕过尾部在背风侧体现出了一定的轴向速度,从而使得旋涡保持一定的稳定性。这也在一定程度上解释了在此攻角下,模型中部的局部压力脉动主频(831 Hz)与尾部主频(689 Hz)不同的原因。
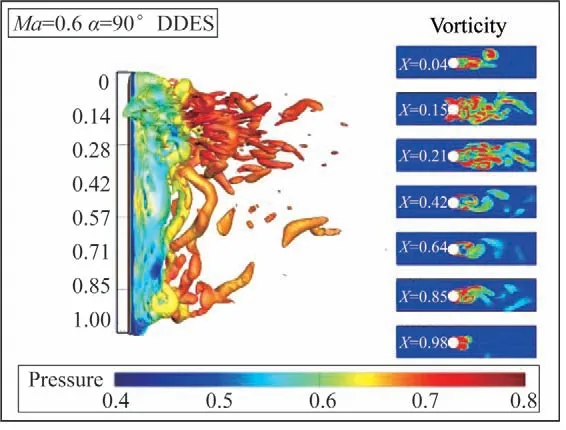
图29 非定常瞬时流动(α=90°)Fig.29 Unsteady transient flow(α=90°)
图30所示为攻角=120°时非定常瞬时流动,图中显示:当攻角大于90°时,流动是从模型尾部(=0.98)开始向头部发展,尾部的流动主要体现为分离流动;随着流动向头部发展,逐渐体现出类卡门涡街的旋涡特征;当流动发展至舵面(=0.21)时,体现为大分离流动,非对称旋涡流动逐渐消失;当流动发展至头部(=0.04)时,受舵面的影响,其流动是大分离流动,并伴有一定的旋涡脱落现象。
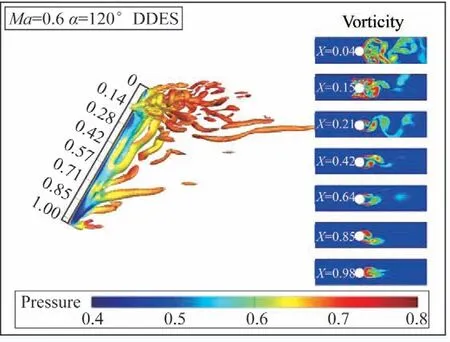
图30 非定常瞬时流动(α=120°)Fig.30 Unsteady transient flow(α=120°)
图31所示为攻角=150°时非定常瞬时流动,流动依然从尾部开始发展,逐渐发展为非对称旋涡流动,由于此攻角存在较大的轴向速度,所以非对称旋涡能够较好的保持,没有出现大范围的旋涡脱落现象。同时,由于旋涡能量较强,当旋涡发展至舵面处时,其与物面距离较近,仍然有较强的诱导能力,所以在舵面上也能够诱导出具有主频的非定常旋涡流动。并且由于攻角效应,旋涡涡位不会太高,在旋涡下方不会诱导出新的旋涡流动,因此在整个弹身的左右涡位是保持一致的,不会出现在不同截面上左右涡位切换的现象。
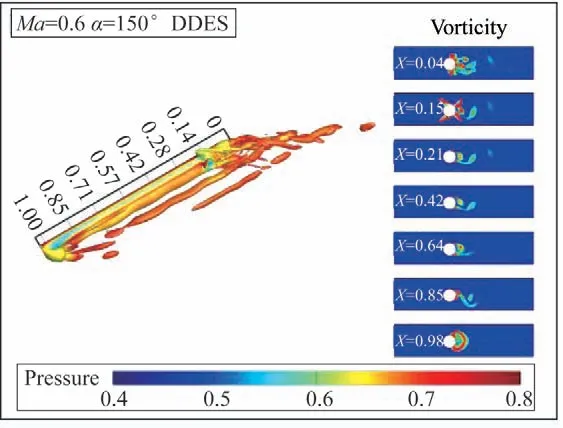
图31 非定常瞬时流动(α=150°)Fig.31 Unsteady transient flow(α=150°)
6 结 论
本文采用非定常数值模拟DDES 方法,计算了细长体在=0.6、0.8、1.15,攻角=0°~180°,侧滑角=0°状态下的非定常流场,并从超大攻角非定常气动力特性、非定常频率特性、非定常旋涡流动特性几个方面进行深入分析,得到以下几点主要结论:
1)试验模型的六分量气动力在攻角45°~165°范围内均具有较为强烈的非定常性,侧向力的非定常脉动幅值尤为强烈,其瞬时量值为法向力的1/4~1/2。
2)试验模型的横侧向气动力(侧向力、偏航力矩、滚转力矩)在攻角45°~165°范围内有比较明显的主频,范围在400~1 400 Hz,纵向气动力/力矩无明显主频。
3)气动力的主频特性主要由旋成体弹身带来,弹翼贡献很小。
4)背风侧复杂旋涡流动是非定常气动力主要原因,其主要体现为旋涡生成、旋涡切换、涡脱落等。
