气动阻尼对裂纹叶片振动特性的影响研究
2022-09-28周震霆刘永葆
周震霆,贺 星,刘永葆
(海军工程大学 动力工程学院,武汉 430033)
在燃气轮机中,叶片作为承担能量转换的核心部件,决定着燃气轮机能否高效、可靠运行,然而其恶劣的工作环境,使得叶片故障成为燃气轮机部件典型故障之一。裂纹是机械损伤中最常见的形式之一,叶片上的裂纹会影响叶片的动态特性和运行稳定。在旋转叶片的研究中,通常将叶片简化为悬臂梁模型[1-2],如常用的Euler-Bernoulli梁模型[3]和Timoshenko梁模型[4]。工程实践中,人们常将裂纹分为张开式裂纹和呼吸式裂纹。长期以来,人们在研究裂纹时,通常假定裂纹处于张开状态[5],而在实际过程中,裂纹会出现闭合状态。人们对此总结分析,Chondros等[6]、Cheng 等[7]、杨海燕等[8]、刘文光等[9]提出了多种呼吸式裂纹模型,更加客观地反映了裂纹的振动过程。压气机叶片在工作过程中,会受到气流激振力和气动阻尼的影响,从而发生振动,当叶片中出现裂纹,结构的振动特性会发生改变。本文采用含裂纹悬臂梁模型模拟带有裂纹的压气机叶片,建立呼吸式裂纹模型,引入余弦力模拟气流激振力,通过改变阻尼大小,探索压气机叶片振动特性随气动阻尼的变化情况。
1 含裂纹梁的刚度模型
1.1 张开式裂纹模型
假设在振动期间,弹性梁表面裂纹始终处于张开状态,忽略裂纹的闭合效应和梁在横向载荷作用下产生的剪切效应,张开式裂纹的刚度可近似表示为[10]:
(1)
式中:ko为裂纹完全张开时梁的刚度,N/m;kc为裂纹完全闭合时梁的刚度,即无损梁的刚度,N/m;kT为裂纹截面处等效弹簧的扭转刚度,N/m。
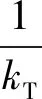
(2)
φ=0.629r2-1.047r3+4.602r4-9.975r5+20.285r6-32.993r7+47.041r8-40.693r9+19.6r10
(3)
式中:L为悬臂梁的长度,m;η=l/L为裂纹的相对位置,其中l为裂纹距固定端的距离,m;ν为泊松比;E为弹性模量,GPa;b为梁的宽度,m;h为梁的高度,m;r=a/h为相对裂纹深度,其中a为裂纹深度,m。
1.2 呼吸式裂纹模型
裂纹在实际振动过程中,大多数处于一种呼吸模式,即裂纹在全开与全闭之间必然存在部分开启的状态。为了较为真实地描述裂纹的“呼吸”过程,杨海燕等[8]采用了余弦呼吸函数:
(4)
余弦呼吸函数可以形象地描述出裂纹在全开和全闭之间的过渡状态。在此基础上,可以利用张开式裂纹和闭合式裂纹梁的刚度,得到呼吸式裂纹梁的刚度表达式为:
(5)
式中:ω为裂纹所受外部激励力的频率;t为激励时间,s。当ωt=2nπ(n=1,2,…)时,裂纹完全闭合,此时呼吸梁模型等效为闭合梁模型,即kbr=kc;当ωt=(2n-1)π(n=1,2,…)时,裂纹完全张开,此时呼吸梁模型等效为张开梁模型,即kbr=ko。
2 含裂纹叶片单自由度的振动建模
取一个均匀、各项同性的含裂纹悬臂梁模拟裂纹叶片,如图1所示。悬臂梁长为L,宽度为b,高度为h,距离固定端l处有一条深度为a的裂纹,距离固定端lp处受到余弦激振力F。
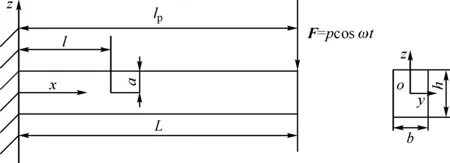
图1 含裂纹悬臂梁模型
忽略裂纹对悬臂梁振动的影响,横向激励力下梁的受迫弯曲振动方程为[9]:
(6)
式中:I为梁的截面惯性矩,m4;c为阻尼系数;ρ为梁的密度,kg/m3;A为梁的截面面积,m2;p为横向激励力的幅值,N;lp为激励力离固定端的距离,m;ω为激励力的角频率,rad/s;δ为Dirac函数,u(x,t)为z方向上振动位移,m;x是与固定端的距离,m;t为激励时间,s。
通过Galerkin法把悬臂梁考虑成单自由度系统,仅考虑一阶模态,假设该裂纹梁的横向固有振动形式为:
u(x,t)=U(x)T(t)
(7)
式中:U(x)为梁横截面中性轴在x处的横向振动幅值函数;T(t)是描述运动规律的函数。
根据悬臂梁的边界条件,得到悬臂梁的一阶振型函数为[11]:
U(x)=[(sinβx-sinhβx)+αn(cosβx-coshβx)]
(8)

将式(7)带入到式(6)中,左右两端同时乘以U(x),并在0至L上积分可得:
(9)
其中:
(10)
(11)
(12)
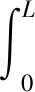
(13)
式中:m*为广义质量,kg;c*为广义阻尼;k*为无裂纹梁的广义刚度,与kc相等,N/m;F*为广义力,N。其中k*可分别用ko或kbr代替,从而得到张开式裂纹梁或呼吸式裂纹梁的振动方程。由于本文采用单自由度系统,可通过公式(14)表示不同形式梁的模态频率。
(14)
式中:ωo为张开式裂纹梁的一阶模态频率,rad/s;ωbr为呼吸式裂纹梁的一阶模态频率,rad/s;ωc为闭合式裂纹梁的一阶模态频率,rad/s。
3 气动阻尼的影响分析
为了较为真实地反映出含裂纹叶片在气流激振力下的振动特性,本文选用呼吸式裂纹梁模型对裂纹叶片进行模拟。所选悬臂梁基本参数如表1所示。

表1 悬臂梁基本参数
3.1 不考虑气动阻尼的影响
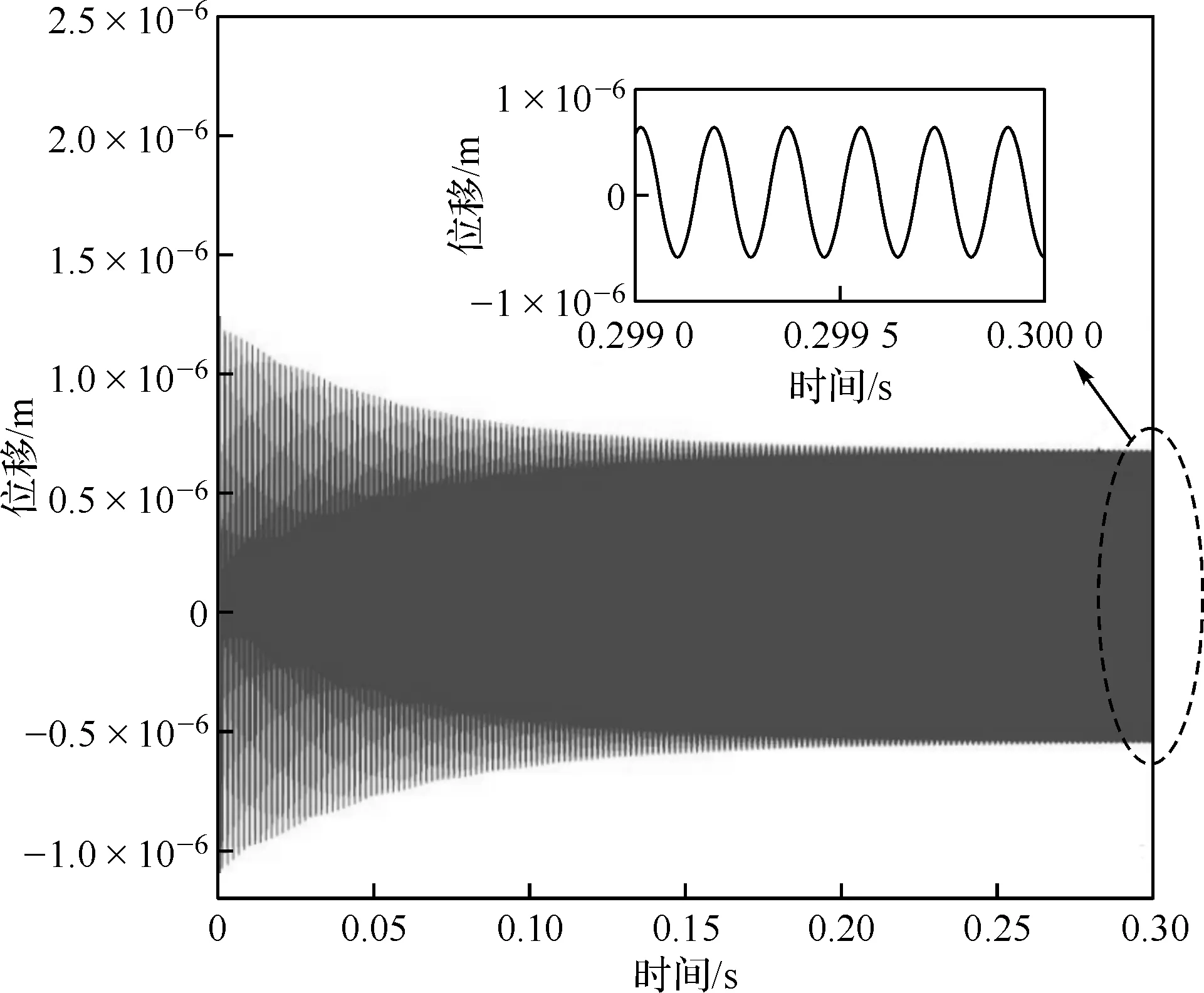
假设气流激振力幅值p=100 N,频率ω=5 600 Hz,如图2所示。呼吸式裂纹梁刚度由图3可以看出,梁的刚度在1.290 5×106~2.064 9×106N/m内波动,即梁在完全闭合时的刚度2.064 9×106N/m,在完全张开时的刚度为1.290 5×106N/m。在计算过程中,取阻尼比ξ=0.05,一阶阻尼系数c可根据ξ=c/2mf计算,其中m为叶片质量,f为叶片固有频率。将得到的广义质量m*、广义阻尼c*、呼吸式裂纹刚度kbr、广义力F*带入公式(9)计算,利用方程的解,通过四阶Runge-Kutta法和快速傅里叶变换等方法计算,得到含呼吸式裂纹梁在外激励下的位移响应图、频谱图以及相图,分别如图4中的(a)、(b)、(c)、(d)所示。

图2 激励力响应
悬臂梁的初始位移为零,采样时间为10-2s,由图4(a)中可以看出,在不考虑气动阻尼的影响下,梁自身的结构阻尼对振动的影响很小,导致梁在外激励作用下的响应经过较长时间达到稳定。同时可以看出,悬臂梁在振动初期振幅并不稳定,即使达到稳态之后,悬臂梁在正向位移响应的大小与负向并不相等,这是由于呼吸式裂纹刚度随时间变化引起的。图4(b)中频谱图出现了很多高频成分,这在前人[12-13]相关研究中出现过,体现出了呼吸式裂纹的非线性特性。从图4(c)和4(d)的相图中可以更加清晰地看到梁在振动初期的不稳定性,也可以更直观地看到梁在呼吸式裂纹作用下所反映出来的稳定阶段正负位移大小不相等的现象。
3.2 考虑气动阻尼的影响
任何结构在实际振动过程中,如果没有持续外力的作用,一段时间后振动都将衰减为零,最后趋于静止。这说明振动结构在自由振动过程中存在着能量的耗散,而引起能量耗散、使结构振幅逐渐减小的特性称为阻尼。结构振动过程中阻尼的来源很多,有材料阻尼、摩擦阻尼、气动阻尼等。材料阻尼为固体材料变形时产生内摩擦或材料快速应变产生的热耗散;摩擦阻尼为结构连接部位的摩擦损耗;气动阻尼为结构外部空气引起的能量耗散。
由于燃气轮机在不同工况下,流过压气机气流的质量流量、流速等条件不同,从而叶片所受气动阻尼不同,导致含裂纹叶片在气流激振力作用下的振动特性发生改变。假设悬臂梁所受激振力不变,考虑气动阻尼对悬臂梁的影响,此时公式(11)变为:
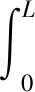
(15)
式中:Δc表示气动阻尼。
本文仅考虑气动阻尼抑制振动的情况。通过阅读文献[14-15],本文选取气动阻尼分别为结构阻尼的0.01倍、1倍及10倍进行研究,将公式(15)带入到公式(9)中进行计算,得到气动阻尼影响下含呼吸式裂纹梁在外激励下的位移响应图、频谱图以及相图,分别如图(5)、图(6)、图(7)所示。

(a) 位移响应图
(a) 位移响应图

(a) 位移响应图

(a) 位移响应图
图(5)、图(6)、图(7)分别为气动阻尼为结构阻尼0.01倍、1倍、10倍时梁的振动特性图。通过对图(4)、图(5)、图(6)、图(7)的比较,从位移响应图中可以看出,随着气动阻尼的增大,梁的振动位移趋于稳定的速度越快;频谱图反映出了气动阻尼与幅频特性的关系,随着气动阻尼的增大,幅值减小,高频峰值减少,梁的振动非线性效果减弱;在相图中,随着气动阻尼的增大,梁的振动位移相对更加集中,侧面反应出梁的振动位移趋于稳定的速度加快,同时也能看出,气动阻尼并不影响呼吸式裂纹的特性。
图8为无气动阻尼和不同气动阻尼作用下位移响应的对比图。从图8中可以看出,虽然在运动过程中只是受到了单个余弦激振力的作用,但是梁在振动过程中的响应并不是一个完整的余弦周期,中间出现了一些其他的倍频幅值,导致梁的振动幅值存在相应的起伏波动。当气动阻尼为结构阻尼的0.01倍、1倍及10倍时,梁的振幅响应整体上呈现出减弱的特点,这说明气动阻尼对梁的振动具有抑制作用,气动阻尼越大,梁的振动幅值越小,同时也可以看出阻尼增大带来的响应滞后现象。
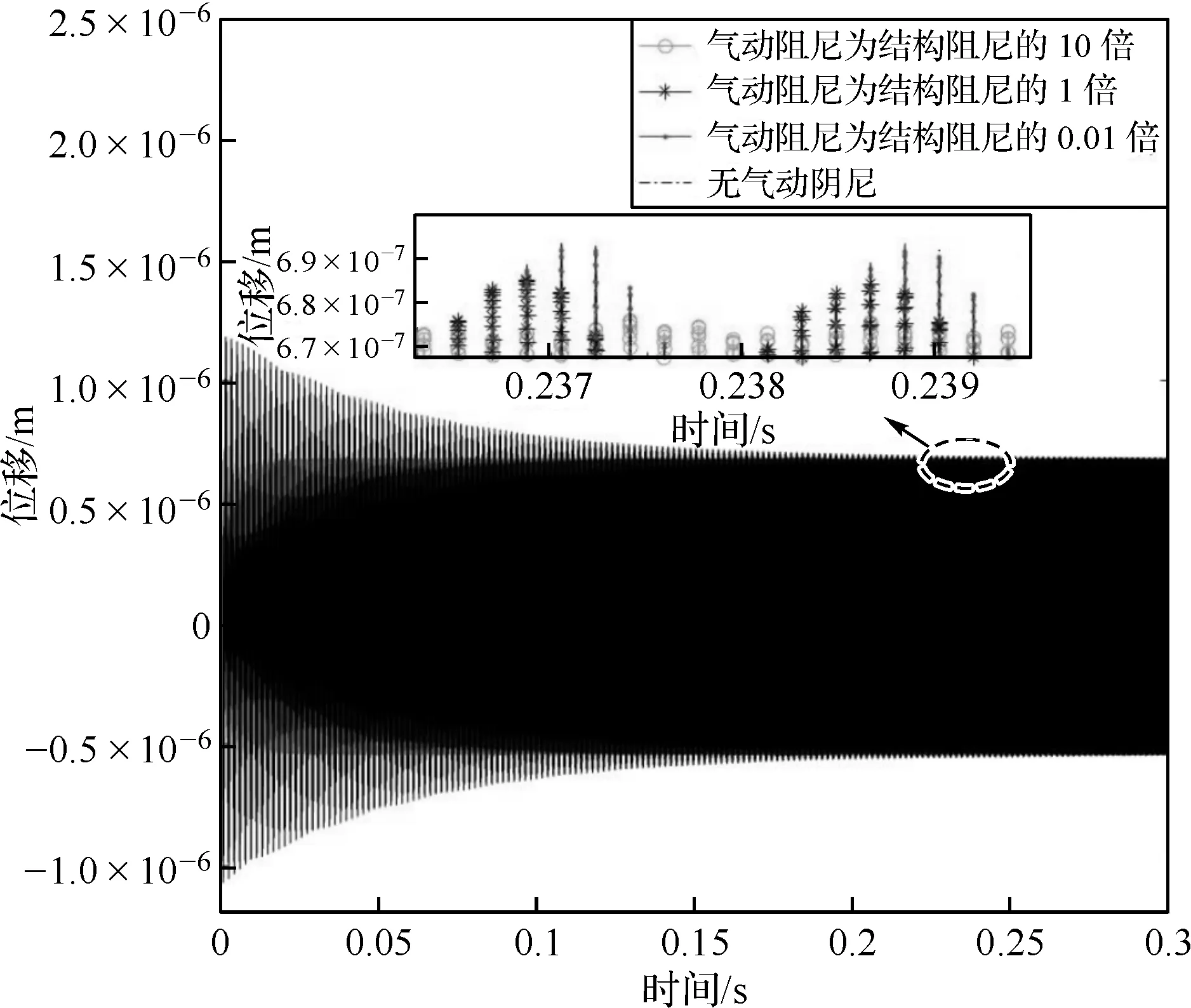
(a) 整体图
4 结论
本文将含裂纹压气机叶片模拟成含呼吸式裂纹悬臂梁,通过在梁端引入余弦激励力和改变阻尼系数大小,模拟研究气流激振力和气动阻尼对含裂纹压气机叶片的振动特性的影响,得出以下结论:
1) 即使是在单个激振力作用下,悬臂梁的振动仍具有很强的非线性,随着气动阻尼的增加,振动的非线性减弱。
2) 气动阻尼的存在影响了梁在稳定阶段的响应幅值,阻尼越大,幅值越小。
本文选取的悬臂梁模型为等截面矩形梁,与实际叶片仍有偏差,之后应在此基础上进行模型的改进,使它更加符合真实叶片。对于气动阻尼的设定,笔者是通过阅读文献进行的定性研究,在实际过程中,可通过有限元仿真或实验等手段进行获取。
