基于分层EOF 的深海声速剖面时变特征建模

张林虎，刘 杨*，刘焱雄，陈冠旭，李梦昊

（1.自然资源部 第一海洋研究所,山东 青岛 266061；2.自然资源部 海洋测绘重点实验室,山东 青岛 266061）

海洋占地球表面积71%，平均深度3 700 m[1]，如今正成为世界各国争夺资源的主战场。一切海洋活动都离不开精密的位置服务，而深海声速随海洋动态环境在1 400～1 600 m/s 的某个区间内变化[2]，成为制约水声精密定位精度的主要因素，因此需对深海声速的变化规律展开研究。高精度的深海声速剖面主要依靠声速仪、温盐深仪进行点位观测获取，受观测手段制约，尚无法对整个目标观测海域的声速场进行全面、连续的观测，因而需要根据实测数据构建观测区域内的声速剖面模型，以获得特定时间和地点的声速剖面。经验正交函数（Empirical Orthogonal Function,EOF）模型法是声速剖面的主要构建方法，它可以通过分析目标海域内历史观测数据的矩阵特征值与特征向量有效提取声速剖面的主要特征[3]。

Leblanc 和Middleton[3]于1980 年首次提出了采用经验正交函数（EOF）分析海洋声速剖面的方法，其后相关研究陆续开展。Davis 试验验证了EOF 作为基函数描述声速剖面的方法具有最小均方根最优性[4]；丁继胜等[5]基于实测声速剖面簇，利用经验正交函数计算了目标海域任意位置处的声速剖面，并依此对多波束边缘数据进行声线折射改正，取得了较好的效果；张旭等[6]基于Argo 数据利用EOF 方法分析了台湾以东海域声速垂直结构的时空变化特征；这些研究表明采用经验正交函数模型分析声速剖面数据是可行的。不同阶数的EOF 表达声速剖面的精度和效率存在差异。Park 等研究认为利用声速剖面簇的前5 阶EOF 就能较为准确地描述任意声速剖面[7]。周士弘和张茂有利用少于5 阶的EOF 描述台湾东北部海域声速场，并尝试采用EOF 方法预报声速剖面[8]。国内外相关工作集中于对浅海声速剖面的研究，而对深海声速剖面的研究则主要基于Argo 浮标观测数据开展。由于Argo 浮标声速剖面观测数据分布稀疏（空间分辨率约为1°）且采样时间间隔较大（10～30 d），不适用于局域较小时间尺度的深海声速剖面特征分析。

由于不同深度处的深海声速剖面存在不同的声速变化规律和特征，以及声速观测设备的观测深度范围不同，所以需要采用分层的方式分析声速剖面。刘杨范等[9]针对声速在浅层水域的复杂性与深层水域的平稳性特点，提出了双层经验正交函数建模法，并采用自适应方法确定出合理的阶次。由于经典深海声速剖面分为混合层、深海声道层和深海等温层三层[10]，因而采用双层正交函数建模法不适用于深海声速剖面。声速时空变化特征与海洋环境相关，陈小宇采用EOF 将声速剖面分为背景场和扰动场，分析了声速变化与潮汐现象之间的关系[11]；孙文舟等提出了一种简化模型解析声速剖面EOF 第一模态时间系数和空间函数变化规律，并认为温度是影响时空变化规律的主要因素[12]。

因此，本文基于较小时间尺度（时间间隔为6 h）的深海声速剖面实测数据，首先分析深海声速观测数据的统计特征，结合经典深海声速剖面分层，将目标海域声速剖面分为上、中、下三层；然后，采用分层EOF 方法分析目标海域不同深度层第一模态时间系数的变化规律，采用2 种时域拟合模型描述时变规律并比较其拟合精度，并利用等效平均声速验证拟合模型的合理性；最后，探究声速剖面周期性变化特性的影响因素。

1 声速剖面分层EOF 建模

1.1 深海声速剖面分层深度选取

不同深度层声速剖面随时间和空间变化的特征不同，需要根据声速时空变化特征对剖面进行分层，以减小不同分层中声速剖面时空变化特征对构建模型的影响。本文利用不同声速剖面簇的同深度标准差、声速标准差梯度、平均声速剖面垂直梯度三种声速剖面统计特征对深海声速剖面进行分层。其中，不同声速剖面簇的同深度标准差表示声速随时间变化的剧烈程度，声速标准差梯度表示同深度标准差随深度变化的程度，平均声速剖面垂直梯度表示声速剖面随深度变化的程度。

假设观测区域内获得M个N层的标准声速剖面数据集。第m层的同深度声速标准差 σm定 义为：

式中：M为第m层声速观测个数；Si为第m层第i次声速观测值；S¯为第m层声速观测均值。

第m层 的声速标准差梯度∇σm定义为：

式中：σm+1为第m+1层同深度声速标准差；Δzm为第m层 的水层厚度。

第m层的声速垂直梯度gm定义为：

式中：Sm+1为第m+1层声速；Sm为第m层 声速。

1.2 分层EOF 方法

假设观测区域内的声速剖面有M个，经过数据预处理，最终获得M个N层的标准声速剖面数据集S。根据经典深海声速剖面变化特点并结合目标海域的声速变化统计特征，可以将标准声速剖面数据集S划分为上、中、下三个深度区间层：

进而，对协方差矩阵求解特征值和特征向量：

式中：λu、λb、λd分别为Ru、Rb、Rd的特征值矩阵，Fu、Fb、Fd分别为Ru、Rb、Rd与λu、λb、λd对应的特征向量。

将特征值按照从大到小的顺序重新排列:

式中：λu、λb、λd分别为Ru、Rb、bd的排序后的特征值矩阵，Fu、Fb、Fd别为Ru、Rb、Rd与λu、λb、λd对应的特征向量，D1、D2-D1、N-D2分别为上、中、下深度区间层解算的特征值个数。

每一个深度层内，模态系数矩阵A定义[14]为：

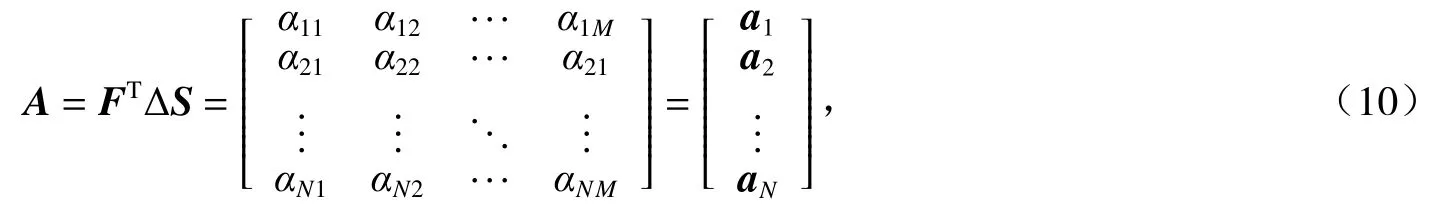
式中：aN为第N阶模态系数。

基于EOF 模态矩阵的方差贡献率[15]，分别在上、中、下三个深度区间层内取前i、j、k个特征值，及其对应的特征向量和模态系数矩阵。以下层为例，特征值矩阵 λdk、特征向量矩阵Fdk及模态系数矩阵Adk分别表示为：

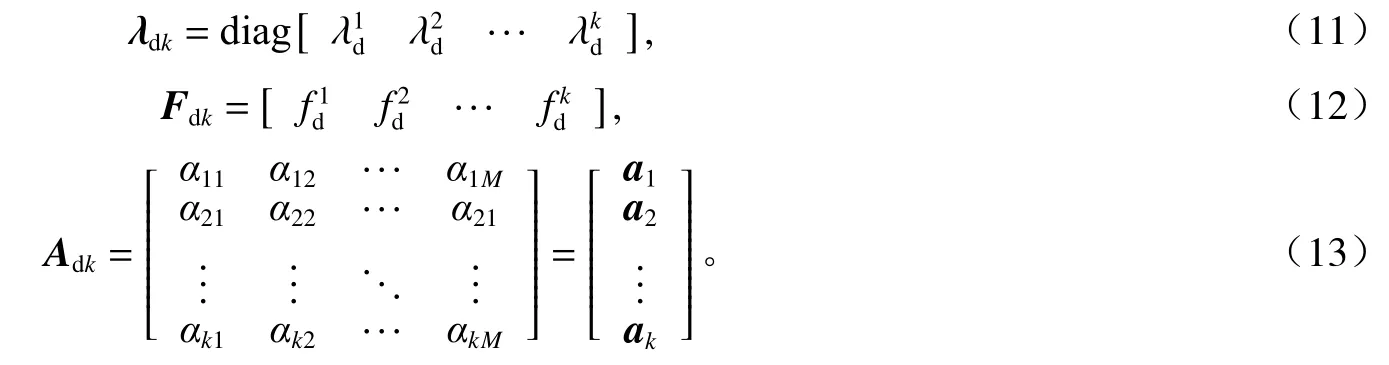
同理可得到λui、Fui、Aui、λbj、Fbj、Abj。对模态系数矩阵进行时变分析，可得到声速随时间的变化规律。对模态系数进行拟合便可获得测量期间任意时刻的模态系数并解算得到任意时刻的声速剖面：

2 结果与分析

2.1 深海声速剖面数据获取及分层

实验数据来自2021 年7 月在南海海域利用声速仪（Sound Velocity Profile,SVP）及温盐深仪（Conductivity,Temperature,Depth,CTD）观测的深海声速剖面数据，其观测间隔为6 h，时间跨度为7 d。采用声速仪及温盐深仪观测获得数据后，需要预处理以获得标准分层的声速剖面数据，处理流程见图1。其中，温盐深仪测量海水中的温度、深度、盐度信息后，根据声速经验公式计算海水声速值。陈长安等[16]对比了10 种声速经验公式在南海海域的精度，建议使用Del Grosso 声速经验公式计算声速，本文采用Del Grosso 声速经验公式计算声速值[17-18]。声速观测过程中，受投放仪器设备故障及海流影响，观测剖面深度不是顺序增加，需基于深度对数据进行重排序，并剔除粗差；对于偏离声速剖面主廓线过大的声速数据予以剔除。基于不同分层的数据分布情况进行不同处理：观测深度以内的缺失数据进行插值；观测深度以外数据进行数据延拓；对相同深度的观测值采用调和平均方法获得该深度处声速值，对于标准间隔深度处的声速则取前后一定深度区间内声速的加权平均值；最后对分层内的声速数据取平均以获得深度间隔为0.5 m 的标准化声速剖面。

图1 声速数据预处理流程Fig.1 Preprocessing flow of the sound velocity data

经过数据预处理，SVP 测量获得12 条有效数据，CTD获得30 条有效数据（图2）。声速剖面具有典型的深海声速剖面分层特征[10]，随深度变化可划分为表面层（混合层）、跃变层和深海等温层，其中跃变层又分为季节性跃变层和主跃变层。声速剖面在水深0～2 m 处，受仪器自身温度的影响，声速变化剧烈且差异较大；在水深2～30 m 左右处，考虑到风浪的搅拌作用导致该水深区间水温相近，声速变化幅度较小，具有明显的表面层特征；在水深50～1 100 m 处，声速值随深度增加而减小，为深海垂直结构中的跃变层；在水深1 000 m 以深的声速剖面结构稳定，层内水温与盐度变化趋于一致，声速主要受压力变化影响，所以，声速随深度增加而增大，具有明显的深海等温层特征。

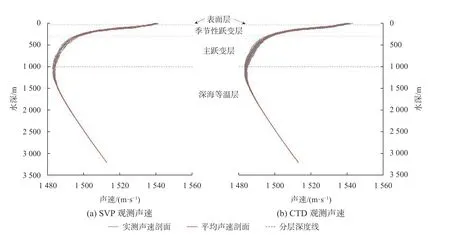
图2 测区声速剖面示意图Fig.2 Sound velocity profiles in the study area

基于实测的声速剖面数据，本文分别统计了SVP 和CTD 测得的声速剖面簇的同深度标准差、同深度声速标准差梯度以及平均声速剖面的声速垂直梯度，见图3 和图4。

由图3 可以看出，不同深度声速剖面标准差为0.02～3.58 m/s，其最大值出现在109 m 水深处，最小值出现在3 130 m 水深处。由图4 可以看出，不同深度声速剖面标准差为0.02～2.86 m/s，其最大值出现在87 m 水深处，最小值出现在2 650 m 水深处。综合图3 和图4 可以发现：在水深0～500 m 左右，声速标准差梯度数值和声速剖面标准差随深度变化剧烈且数值较大，声速垂直梯度为负值且梯度绝对值由大到小，并趋近于0；在水深500～1 500 m 左右，同深度声速标准差梯度数值变化趋缓且呈现变小趋势，不同深度声速剖面标准差变化剧烈程度变小且具有随深度变化缓慢降低的趋势，声速垂直梯度缓慢趋近于0；在水深1 500～3 200 m 左右，不同深度声速剖面标准差、同深度声速标准差梯度和声速垂直梯度基本稳定，数值均趋近于0。

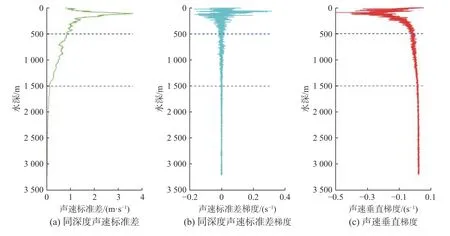
图3 SVP 测量声速剖面数据统计特征Fig.3 Statistical characteristics of the sound velocity profile data measured with SVP

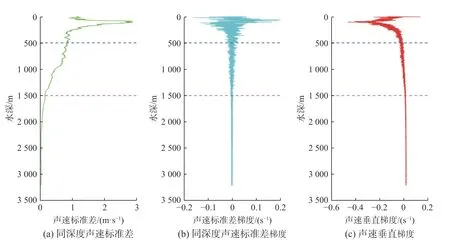
图4 CTD 测量数据声速剖面统计特征Fig.4 Statistical characteristics of the sound velocity profile data measured with CTD

针对不同深度区间声速变化差异并顾及分层点，应尽量选择在声速变化较缓慢的深度[19]，故本文将实测数据声速剖面分为0～550 m、450～1 550 m、1 450～3 200 m 三层，为避免出现边界声速不匹配的情况，不同分层之间设置了100 m 深度区域的重叠部分。

2.2 分层EOF 第一模态系数时变分析

对声速剖面簇进行分层EOF 分析时，在不同分层，采用适当的EOF 阶数能提高运算速度，降低计算数据量，因此，需要选取合适阶数的特征向量和特征值。通常，EOF 各阶次方差贡献率及累计方差贡献率[15]能够反映模态分析的有效性，并为分层EOF 阶数的选择提供依据。前m阶EOF 累积贡献率Ekm定义为：

式中：k为分层内协方差矩阵的行数；λi，λj分别为第i和第j个特征值。

对测量数据进行分层EOF 分解，SVP、CTD、SVP+CTD 观测数据的结果获得上、中、下三层各阶次方差贡献率与阶数的关系，上层声速剖面利用前3～4 阶获得的反演声速剖面，EOF 方差贡献率即可达到99%；中、下层声速剖面利用前2 阶获得的反演声速剖面，EOF 方差贡献率即可达到99%，如图5 所示。整体而言，不同声速剖面簇的第一阶次分层EOF 方差贡献率均在79%以上，分层EOF 第一模态系数能够反映声速剖面随时间变化的主要特征。

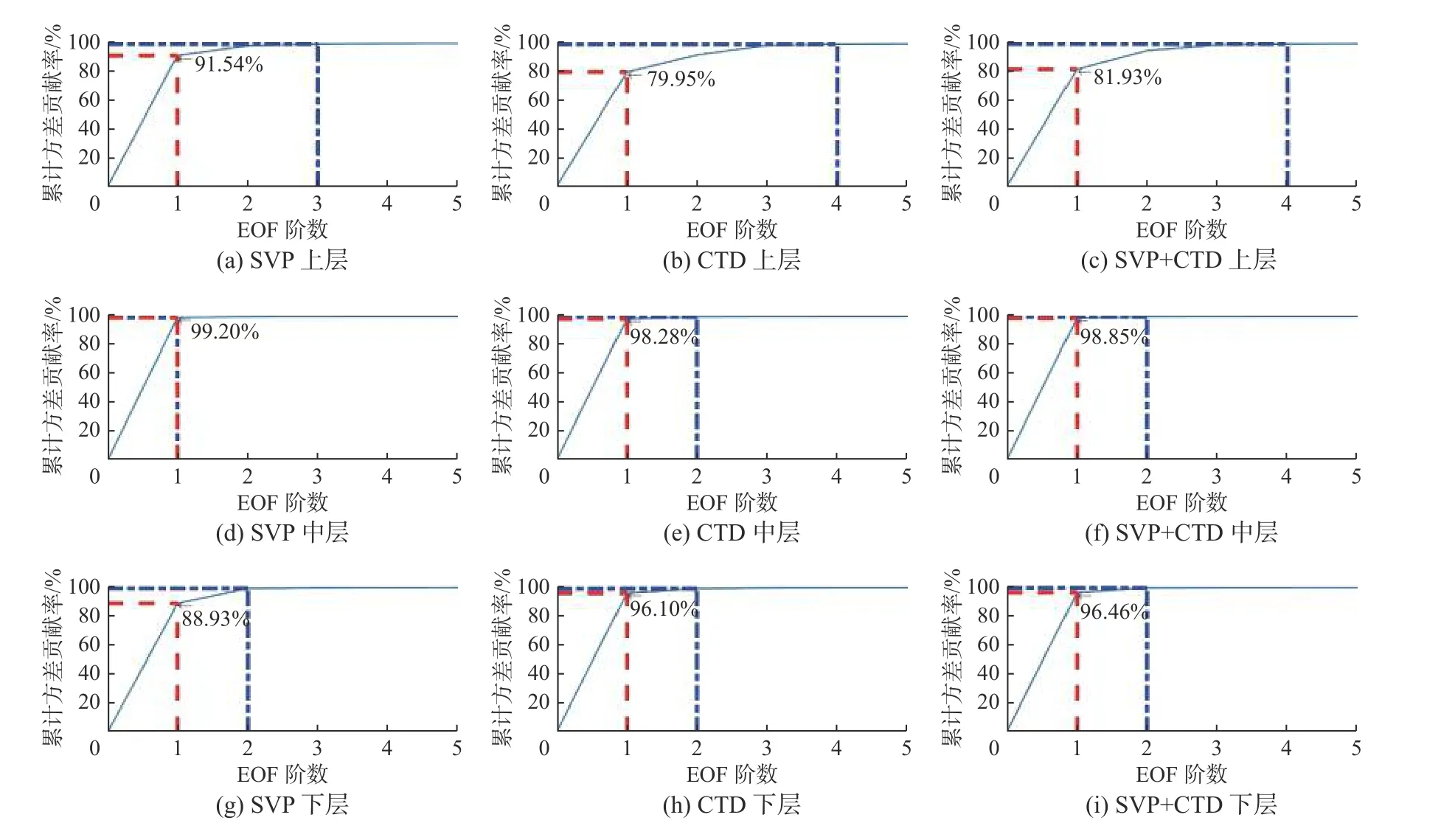
图5 EOF 累计方差贡献率与阶数的关系Fig.5 The relation between the accumulated variance contribution rate and the order of the EOF

本文通过分析分层EOF 第一模态系数研究声速剖面的时域变化规律，假设声速剖面时变规律CT符合正弦变化，则：

式中：TD为声速剖面观测的以天为周期的时间；A1、A21、A22为常数项和周期项系数，其中A21=A2·cos(φ)，A22=A2·sin(φ)。

基于SVP 和CTD 声速剖面观测数据集，以及2 种数据的所有观测结果组成的声速剖面观测数据集（简称SVP+CTD 数据集）对深海声速剖面进行分层EOF 分析，采用一阶傅里叶函数拟合分层EOF 第一模态系数的日周期变化规律，拟合结果（图6）表明，上、中层EOF 第一模态系数的日变化规律均较明显，其中中层较上层日变化规律更加明显，其数据拟合误差见表1。

表1 第一模态系数拟合残差标准差Table 1 The standard deviation of fitted residuals of the first mode coefficients of EOF

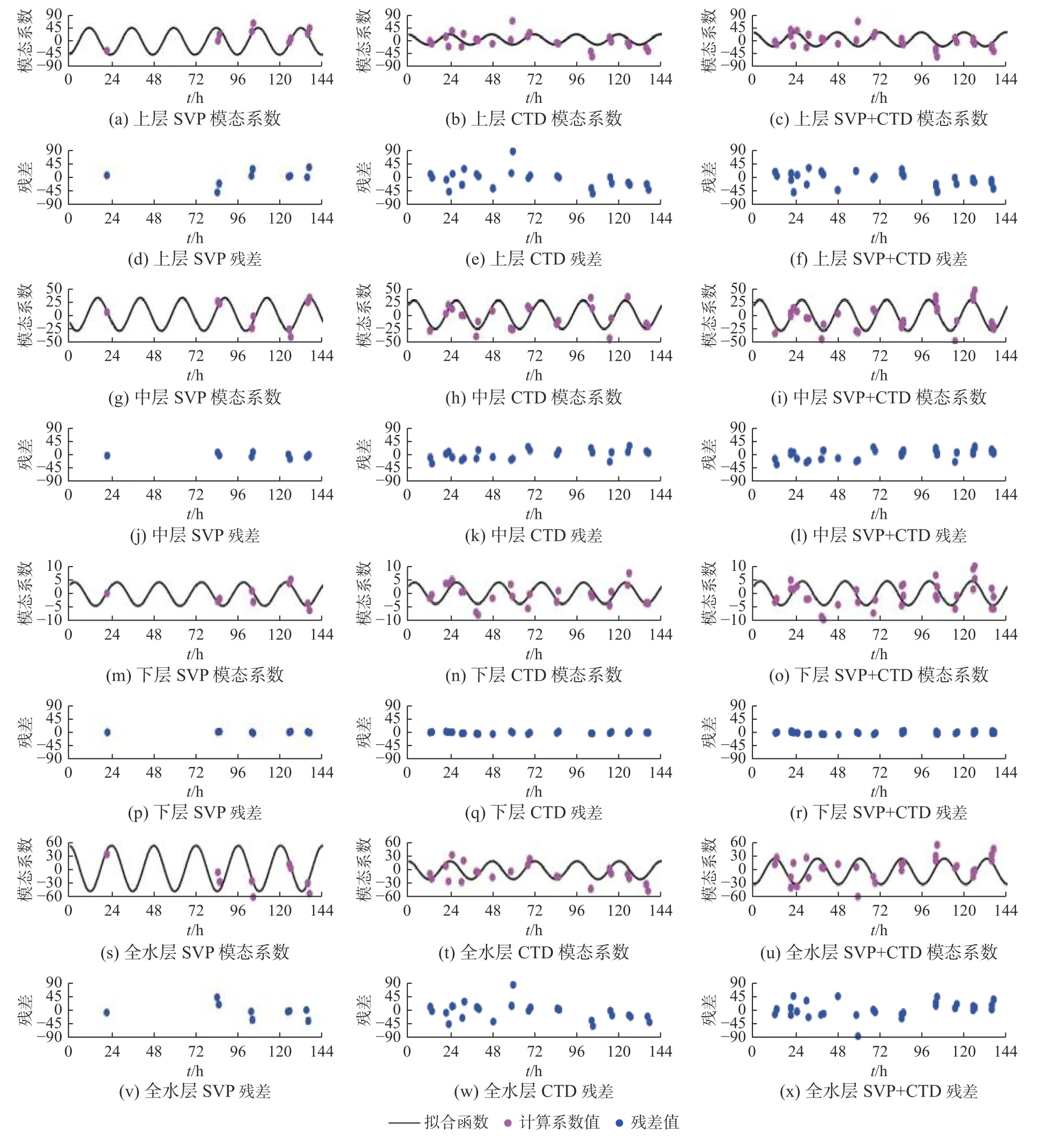
图6 不考虑长期线性变化项的第一模态系数时间变化Fig.6 The temporal variations of the first mode coefficient of EOF without considering the long-term linear variation term

声速剖面的时域变化具有日周期、季节性和年际变化特征，声速剖面测量时间跨度约为一周，其时域变化会受到季节性和年际长期项的影响，同时长期项引起的声速剖面时域变化在观测期间近似可视为线性变化，故在一阶傅里叶拟合基础上添加线性项并进行对比分析。拟合日周期的分层EOF 第一模态系数变化的方法为：

式中：MN1(TD,H)为第一模态系数的时变规律项；TD为声速剖面观测的以天为周期的时间；H为声速剖面观测与首次声速剖面观测的时间延迟；a1、a2、a3、a4为拟合系数，由最小二乘法计算获得。

对深海声速剖面进行分层EOF 分析，采用添加线性项的一阶傅里叶函数拟合分层EOF 第一模态系数的日周期变化特征，拟合结果如图7 所示。由图7 可知：不同分层的EOF 第一模态系数时变规律特征不同；中层比上层第一模态系数日周期变化特征更明显。对比2 种模型的拟合残差标准差（表1）发现，所有分层及不同种类数据在添加线性项之后，拟合效果基本有所改进，且中层改进幅度大于其他层。

图7 考虑长期线性变化项的第一模态系数时间变化Fig.7 The temporal variations of the first mode coefficient of EOF with the consideration of the long-term linear variation term

2.3 声速剖面时变特征分析

在EOF 分析过程中，对分层EOF 模态系数进行拟合可获得测量期间任意时刻的模态系数，并解算得到任意时刻的声速剖面，但模态系数不具有明确的物理意义。因此，本文采用添加线性项的一阶傅里叶函数拟合分层等效平均声速的日周期变化特征，基于等效平均声速的日周期变化特征进一步反映声速剖面的时变特征。拟合日周期的分层等效平均声速变化的方法为：

式中：ES(TD,H)为等效平均声速的时间变化项；TD为声速剖面观测的以天为周期的时间；H为声速剖面观测与首次声速剖面观测的时间延迟；a1、a2、a3、a4为拟合系数，采用最小二乘法计算获得。通过采用添加线性项的一阶傅里叶函数拟合分层等效平均声速结果发现，不同分层声速剖面均具有日周期变化特性，中层日周期变化特征较上层日周期变化特征更明显（表2 和图8）。声速剖面的等效平均声速与第一模态系数变化规律一致，说明第一模态系数的时域变化特征反映声速剖面的时域变化特征。

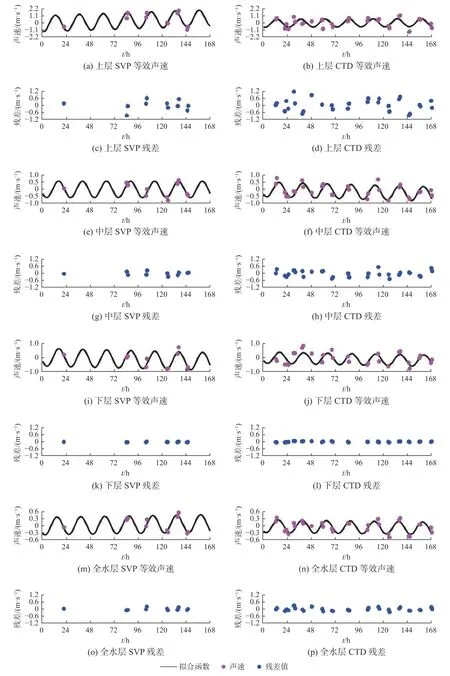
图8 考虑长期线性变化项的等效平均声速时间变化Fig.8 The temporal variations of the equivalent average sound velocity with the considerationof the long-term linear variation term

表2 等效平均声速拟合残差标准差（m·s-1）Table 2 The standard deviation (m·s-1) of fitted residuals of the equivalent average sound velocity

2.4 影响因素分析

EOF 第一模态系数变化的影响因素有温度日变化和年变化引起的海水声速周期性变化，且影响随深度增大而减小[11]。本文首先将第一模态系数与温度做相关性分析，结果见表3。从表3 中可以看出，分层EOF第一模态系数与温度数据具有显著相关性。考虑到太阳辐射对海水温度的影响主要集中于表层至500 m 以浅的区间[11]，推测中层声速或温度变化主要由潮流所致。为此，本文分析声速与潮汐之间的关系。

表3 EOF 第一模态系数与等效平均温度相关系数Table 3 The correlation coefficients between the first mode coefficient of EOF and equivalent average temperature

基于实验海区附近东沙岛验潮站2021 年4 月1 日至5 月30 日的潮汐逐时预报数据（http://global-tide.nmdis.org.cn/），利用T_TIDE 潮汐处理软件包[20]对潮汐数据进行调和分析，获得主要分潮的调和常数，结果见表4。由表4 可以看出，声速实验区域内声速剖面观测时间段，潮汐的主要影响分潮为 O1分潮和 K1分潮。

表4 主要分潮调和常数Table 4 Tidal constants of the major tidal constituents

根据获得的分潮振幅，即可获得区域的潮汐类型[22]，潮汐类型指标F计算方法为：

式中:HO1、HK1、HM2为O1、K1、M2分潮振幅。当F≤0.5时，潮型为半日潮；当0.5 ＜F≤2.0时，潮型为不规则半日潮；当2.0 ＜F≤4.0时，潮型为不规则全日潮；当F＞4.0时，潮型为全日潮[23]。

在声速剖面观测时间段，实验海域潮汐的F值为2.47，潮汐类型为不正规全日潮，与余慕耕[24]对南海该区域潮汐分布特征的描述一致，与本文提取的声速剖面时变特征也基本吻合。

3 结论

针对南海海域实测的全海深声速剖面，本文提出基于分三层的经验正交函数法分析声速剖面的时域变化特征，并构建局域小时间尺度声速剖面模型对声速时域变化特征进行拟合。根据典型深海声速剖面结构和实测数据不同分层的统计特征，将实测数据深度分为上（0～550 m）、中（450～1 550 m）、下（1 450～3 200 m）三层。对每层声速剖面进行经验正交函数分解，获得模态系数矩阵，并分析第一模态系数的时域变化，获得其日变化特征，进而采用2 种模型对声速剖面第一模态系数进行拟合，得到结论如下。

1）实验海区声速剖面分层EOF 第一模态系数及等效平均声速具有日周期变化特征，上层声速日周期变化特征不明显，中层声速日周期变化特征较明显，下层声速变化较小但仍具有日周期变化特征。

2）对于局部海域小时间尺度声速剖面变化拟合过程，应考虑声速剖面长周期变化项的影响。

3）实验海区声速剖面EOF 第一模态系数变化与温度显著相关，声速剖面时变特征与海区潮汐周期特征相似。

声速剖面的时域变化特征影响因素的分析局限于对相关关系的研究。下一步本研究工作将对影响因素进行全面分析并分析其因果关系，同时采用不同声速观测值进行模型计算，由于观测仪器精度和系统误差存在差异，需要在声速剖面数据集解算过程中对不同声速剖面数据进行定权处理。