非定常条件下OWC 径向透平冲击式动叶片优化研究
2022-09-28韩孜乾张晓霞许传礼
韩孜乾,刘 臻,张晓霞,许传礼,杨 鑫
(中国海洋大学 工程学院,山东 青岛 266100)
波浪能是海洋能中储量最大的清洁能源,波浪能转换装置可将波浪能转换为电能,近年来,世界各地的沿海国家纷纷加大对波浪能转换装置的研发力度[9-12]。振荡水柱波能发电装置(oscillating water column wave energy convertor,OWC)具有结构简单、安装维护成本低及使用寿命长的优点,是发展较成熟的波浪能转换装置之一[13]。OWC 利用入射波运动带动气室内部液面上下移动,产生往复气流,实现由波浪能到空气动能的转换;往复气流带动气室顶部的空气透平单向旋转,实现由空气动能到透平转轴动能的转换;转轴带动发电机工作将转轴动能转换为电能。空气透平作为OWC 能量转化的关键部件,其性能的优劣对装置的工作性能有较大影响。径向空气透平转轴所受轴向应力小于轴流式透平,且动叶片无需采用三维实心叶片,节省材料的同时还可降低动叶片转动惯量,在小转速下便可获得较大输出扭矩。基于上述优点,径向透平受到了研究人员的广泛关注。Setoguchi 等[14]通过物理模型试验研究了径向透平的运行特性,研究表明导流叶片安装角较小时,透平吸气阶段的效率比呼气阶段的效率高;内、外侧导流叶片的最优安装角均为25°。Marjani 等[15]采用滑移网格技术模拟透平内部流动,研究表明呼气阶段气流在导流叶片处产生的能量损失导致透平呼气阶段的效率低于吸气阶段的效率。Pereiras 等[16]发现叶片曲率、通道面积会影响上游导流叶片与动叶片之间的能量损失;增大导流叶片的径向长度既有利于导流,又能增加偏转矩。优化后的透平呼气阶段的效率提高了9%,吸气阶段的效率保持不变。Elatife 和Marjani[17]采用试验设计(Design of Experiments,DOE)方法对透平进行优化,涉及的结构参数包括吸力侧半径、叶片弦长、两圆弧中心位置和动叶片前、后缘几何角。结果表明优化后透平的最大峰值效率能达到70%。Elatife 和Marjani[18]发现动叶片结构型式对透平性能影响最大,采用圆形剖面动叶片透平的效率比原型透平的效率提高约19%。Gato 等[19]提出了一种新型双径向自整流空气透平,该透平使用的两排或多排导流叶片增加了导流叶片流域的自由空间。研究表明,多排导流叶片透平阻尼较小,峰值效率比单排导流叶片透平高约3.2%。
研究表明,如果径向透平的相对流动角与动叶片的叶片几何角不匹配,动叶片吸力面将出现明显的流动分离现象[18],改变动叶片吸力面形状可使叶片几何角与相对流动角相匹配,从而提高透平工作性能。本文在动叶片通道宽度和压力面型式不变的前提下,设计了5 种不同厚度的动叶片(5 种动叶片的叶片几何角不同),并采用数值模拟方法研究动叶片厚度对透平非定常性能的影响。
1 研究方法
1.1 透平参数
1.1.1 透平结构参数
本文研究的OWC 径向透平由固定段(图1a)和旋转段(图1b)两部分组成,固定段包括气室、导流叶片及导流叶片盘,旋转段包括转向结构、动叶片及转盘。透平主要结构参数如表1 所示。
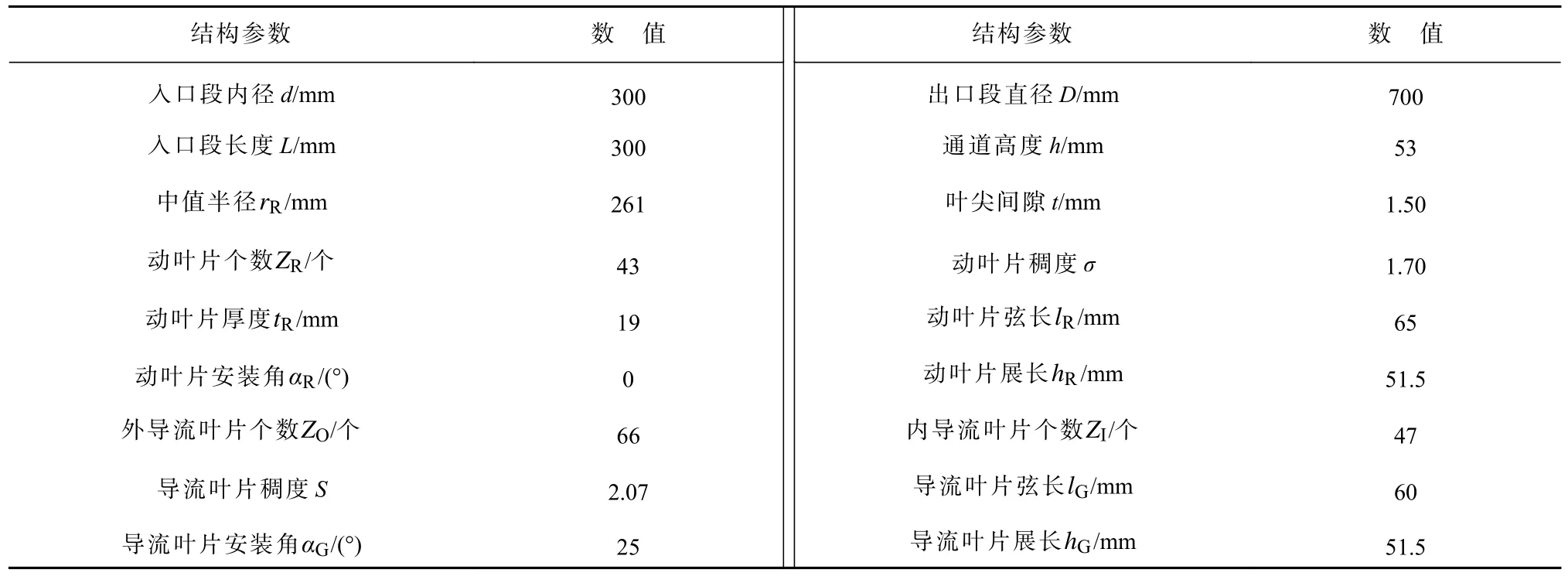
表1 径向透平主要结构参数Table 1 Main structural parameters of the radial flow turbine
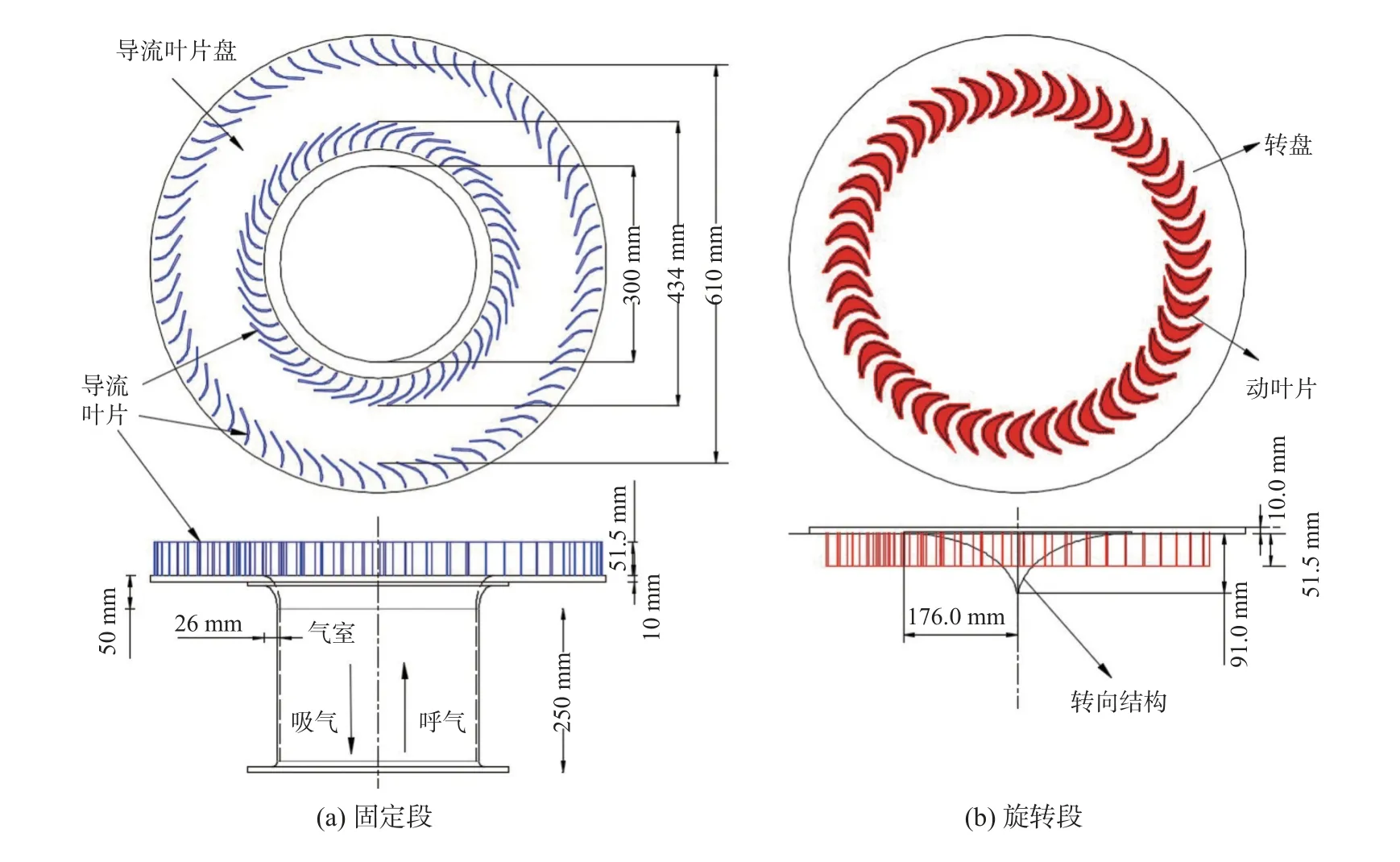
图1 径向透平结构Fig.1 Structure of the radial flow turbine
由于径向透平动叶片吸力面存在明显流动分离现象,因此需合理设置吸力面形状以提高透平工作性能。在动叶片弦长、开口角、安装角和压力面形状不变的前提下,本文共设计5 种厚度分别为7 mm、13 mm、16 mm、19 mm 和22 mm 的动叶片,同时确定动叶片数量分别为117 个、63 个、51 个、43 个和37 个,以保证总气流通道宽度不变。5 种动叶片结构如图2 所示。
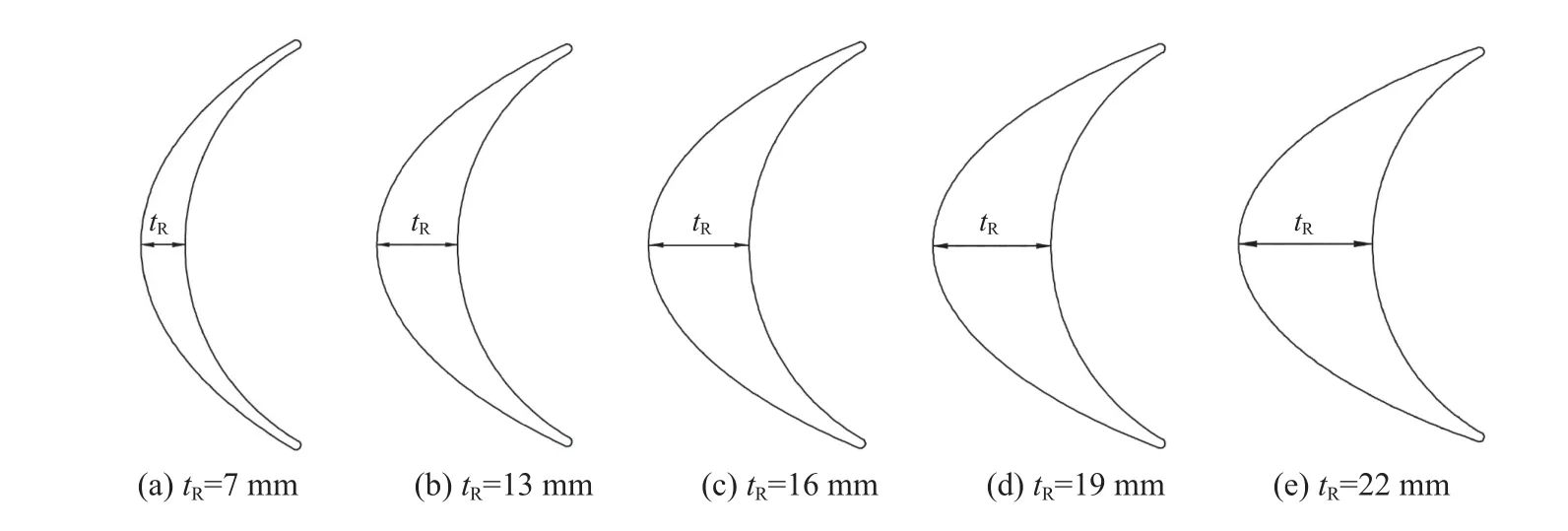
图2 不同厚度动叶片Fig.2 Rotor blades with different thickness
1.1.2 透平性能参数
甘肃省河西内陆河流域总面积27万km2,包括石羊河、黑河、疏勒河(含苏干湖区的哈勒腾河等)等3个水系。年径流量在1亿m3以上独立出山的河流有15条,其中石羊河水系6条;黑河水系6条;疏勒河水系3条。水资源总量61.3亿m3,人均水资源量1 250 m3,耕地亩均水资源量570 m3,分别为全国平均水平的54%和38%,属资源性缺水地区。
相对于定常研究,非定常研究获得的透平输出扭矩、压强等参量的瞬时变化规律更有助于揭示透平真实运行特性。在实际海况下,OWC 内部气流为不规则气流,可看作是若干不同周期、频率的正弦气流的叠加。故可用正弦往复气流代替不规则气流来研究透平非定常性能。研究透平非定常性能参数可定性分析透平输出扭矩、转速、中值半径处气流流速、上下游压差和流量等物理量对透平工作性能的影响。
透平非定常性能评价参数(无量纲数)中扭矩系数CT、输入系数CA和流量系数Φ的表达式如下:

式中:T0为透平周期平均扭矩;ρ为理想气体密度;va为动叶片中值半径处径向峰值流速;Ua为动叶片圆周速度;AR为动叶片中值半径处气流通道面积;rR为动叶片中值半径;ΔPa为动叶片上下游压差峰值。AR、va和Ua的表达式如下:

式中:Va为入射气流峰值流速;d为入口段内径;h为通道高度;ω为动叶片转速。
透平的瞬时输入、输出功率均随时间不断变化,因此需通过周期平均效率 η-评价透平非定常性能,其表达式如下:

式中:T为透平入射气流周期;T1为瞬时输出扭矩;ΔP为上下游瞬时压差;Q为瞬时流量。
1.2 数值模型构建
本文利用SolidWorks 软件构建透平三维几何模型,使用CAE(Computer Aided Engineering)前处理软件ICEM CFD 简化几何模型壁面厚度并划分网格。根据叶片径向布置特点将整个计算域划分为4 部分,沿转轴向外依次为气室区域、环形内侧导流叶片区域、环形动叶片区域和环形外侧导流叶片区域。结构简单的气室计算域采用非结构化网格,其余计算域均采用结构化网格,各相邻区域边界通过Interface 连接。为保证数值模拟的准确性,在动叶片和导流叶片处添加边界层网格,近壁面无量纲壁面距离在5 左右;采用UDF(User-Defined Function)程序控制网格运动和气流输入条件。具体的网格划分如图3 所示。
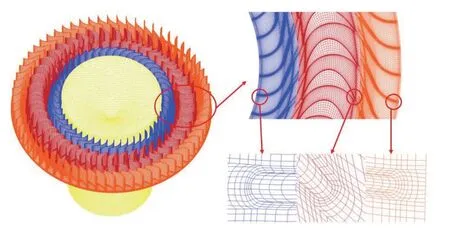
图3 模型计算网格划分Fig.3 Grid division for the model calculation
将网格模型导入Ansys-Fluent 软件进行瞬态数值计算。该软件使用有限体积法求解连续性方程和纳维-斯托克斯方程,流动模型通过压力求解器来求解不可压缩的流体动量守恒方程,其中扩散项和对流项分别采用中心迎风格式和二阶迎风格式进行离散,使用SIMPLE 算法进行压力-流速耦合,使用realizablek-ε湍流模型闭合雷诺时均方程。
1.3 数值模型验证
本文透平的数值模型为全流域模型,结构复杂,网格数对计算结果影响较大,因此本文需进行网格无关性验证。
为了对数值模拟提供数据支持,首先需进行正弦往复气流下的物理模型试验。图4 为试验平台简图,试验平台包括往复造流风洞、径向透平、数据采集及控制系统三部分。往复造流风洞如图5a 所示,验证试验中风洞推板行程和频率分别为0.25 m 和0.6 Hz,能产生峰值流速和周期分别为3.34 m/s 和1.67 s 的正弦气流。透平和数据采集及控制系统如图5b 所示,透平尺寸见图1,电磁离合器和伺服电机能使转轴在不同预定转速下恒定转动。将采集系统采集的入口峰值流速代入式(5)可得中值半径处的径向峰值流速,将采集系统采集的转速代入式(6)可得动叶片圆周速度,将中值半径处的径向峰值流速和动叶片圆周速度带入式(3)可得流量系数,将采集的扭矩、压强等参量代入式(1)、(2)、(7)可得透平输入系数、扭矩系数和周期平均效率。
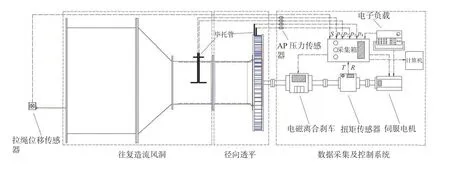
图4 往复气流试验平台Fig.4 Platform for reciprocating airflow experiment

图5 往复造流风洞实物图Fig.5 Photos of the wind tunnel for making reciprocating airflow
本文对动叶片厚度为19 mm 的透平数值模型进行网格无关性验证,时间步长取0.005 s,网格数分别取4.0×106(粗网格)、5.5×106(中间网格)和7.0×106(细网格)。将数值计算结果与试验数据进行对比,结果如图6所示,图中横坐标为流量系数Φ,纵坐标依次为透平输入系数CA、扭矩系数CT及周期平均效率η¯。综合考虑计算精度和时长,选取网格数量为5.5×106的数值模型。
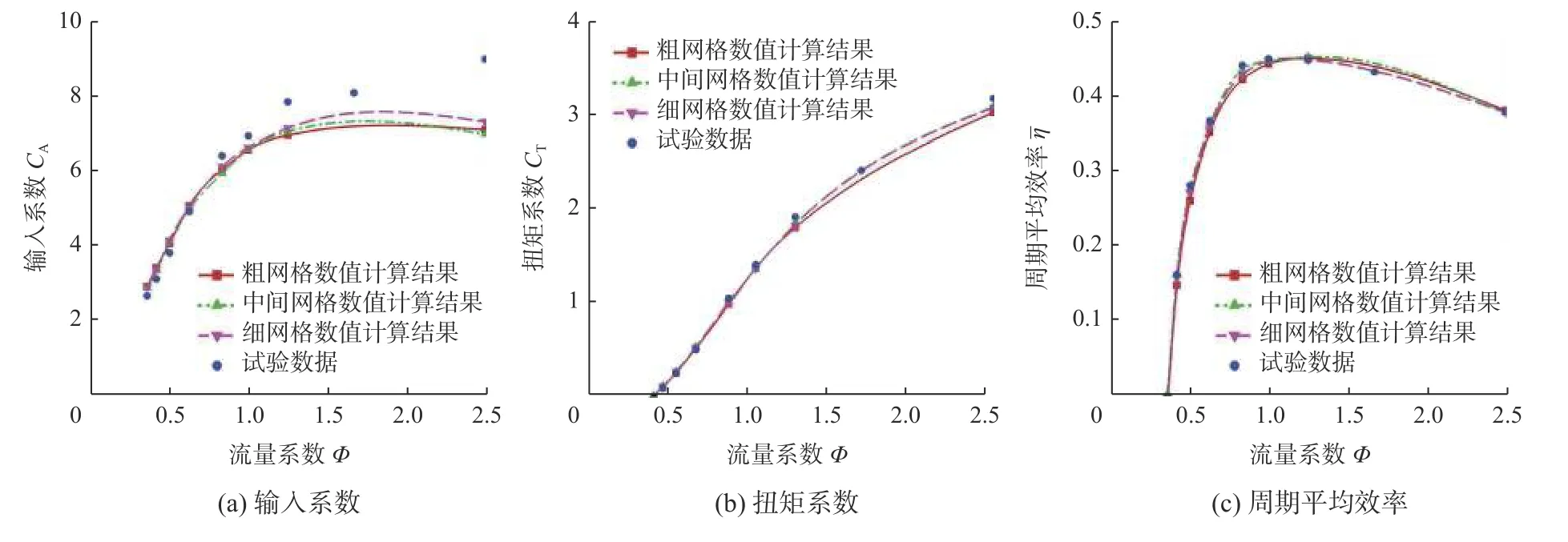
图6 网格数对透平的影响Fig.6 Effect of grid number on the turbine efficiency
2 数值计算结果
本文通过控制转速来覆盖透平工作范围,数值计算中所有工况均在典型气流条件(峰值流速Va=3.34 m/s、周期t=1.67 s)下进行。在只改变动叶片厚度的前提下,通过透平动叶片附近流速云图和压力云图分析动叶片厚度对流场的影响;通过输出扭矩和上下游压差时程曲线分析动叶片厚度对输出扭矩和上下游压差的影响;最后通过透平非定常性能评价参数探究动叶片厚度对透平非定常工作性能的影响。从吸力面增大动叶片厚度时,动叶片吸力面曲率不断增大,将加重吸力面背流侧的流动分离现象,造成更大的流量损失;反之,动叶片厚度减少时,为保证动叶片通道宽度不变需增加动叶片个数,动叶片与气流间的摩擦损失也将增大,因此存在一个最佳动叶片厚度使透平达到最佳工作状态。
2.1 流场分析
利用可视化处理软件Tecplot 360 对Ansys-Fluent 软件得到的动叶片流域的压强和气流流速进行可视化处理,得到不同动叶片厚度下动叶片的压力云图和流域流速云图,以此分析流场的变化。
图7 和图8 分别为转速 ω=120 r/min 时5 种不同动叶片厚度的透平呼气、吸气阶段动叶片附近的速度云图。可以看出,无论是呼气还是吸气阶段,随着动叶片厚度的增大,动叶片流域通道由窄变宽,动叶片迎流侧高流速区面积和通道两侧曲率差异逐渐增大;动叶片前缘的叶片几何角逐渐减小,而相对流动角逐渐增大,两角差距逐渐增大,加剧了压力面迎流侧的流动分离。呼气阶段,沿着气流方向的动叶片流域通道宽度逐渐增大,相对流动角和动叶片几何角的差异增大,加剧了流动分离,并产生更大的负扭矩;而吸气阶段,沿着气流方向的通道宽度逐渐减小,一定程度上减小了相对流动角和动叶片几何角的差异,削弱了吸力面处的流动分离,避免产生较大的负扭矩。
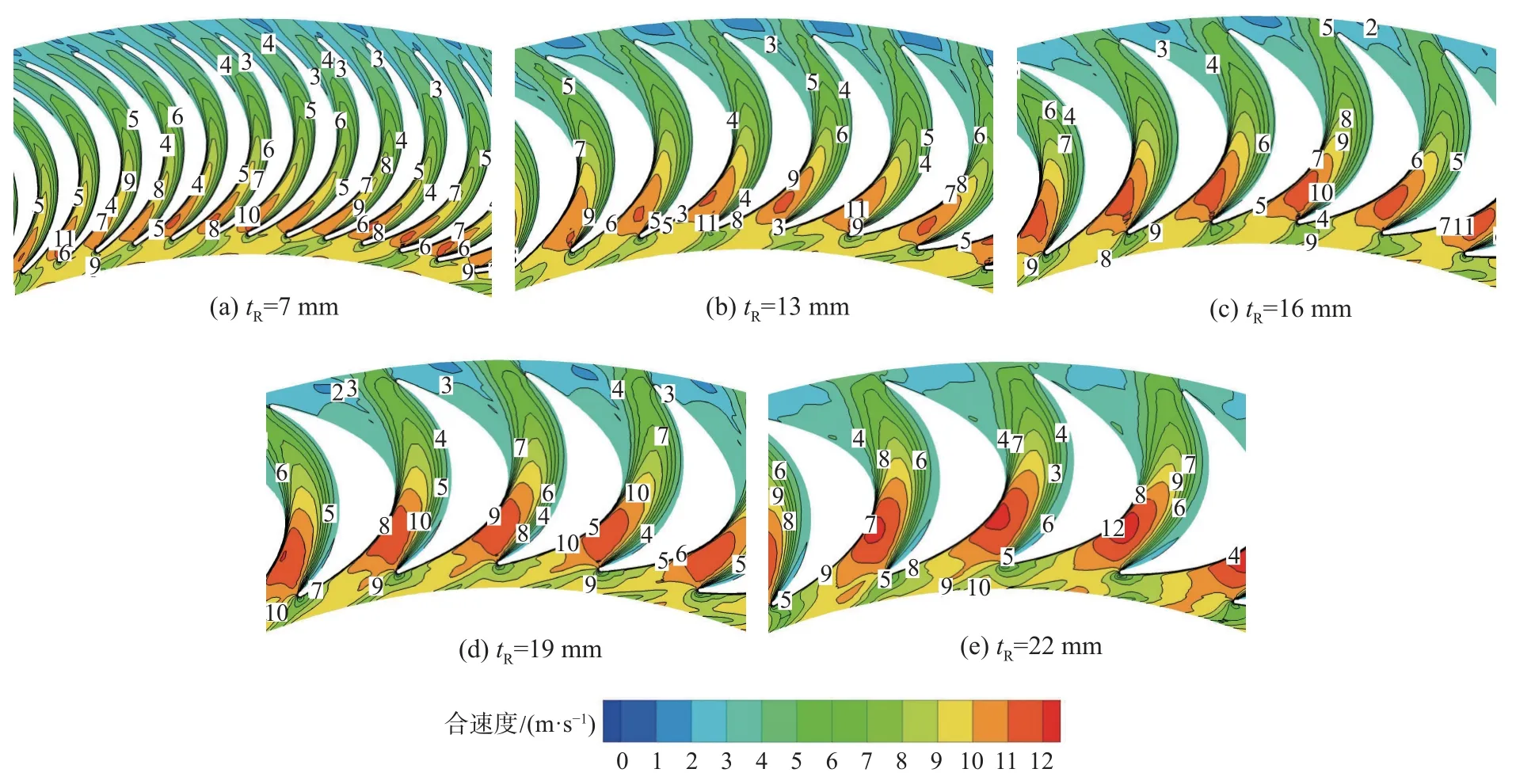
图7 呼气阶段动叶片厚度对叶片附近速度云图的影响Fig.7 Influence of the rotor blade thickness on the speed cloud map near the blade during the exhale stage
图8 吸气阶段动叶片厚度对叶片附近速度云图的影响Fig.8 Influence of the rotor blade thickness on the speed cloud map near the blade during the inhale stage
图9 和图10 分别为转速 ω=120 r/min 时5 种不同动叶片厚度的透平呼气阶段动叶片吸力面和压力面压力云图,气流均为自上而下。由图9 可知,随着动叶片厚度的增大,呼气阶段动叶片吸力面压强整体先减小后增大,沿着气流方向转子上下游压强的差值先减小后增大,而迎流侧高压区逐渐向背流侧扩散导致中部低压区面积逐渐减小;吸力面中部相对低压区的面积和压强量值均逐渐减小。由图10 可知,随着动叶片厚度的增大,呼气阶段动叶片压力面上中部相对高压区和远离转盘侧的高压区先分离再融合;迎流侧负压区面积先增大后减小。呼气阶段吸力面、压力面之间的平均压差基本不变,故产生的扭矩值基本不变。
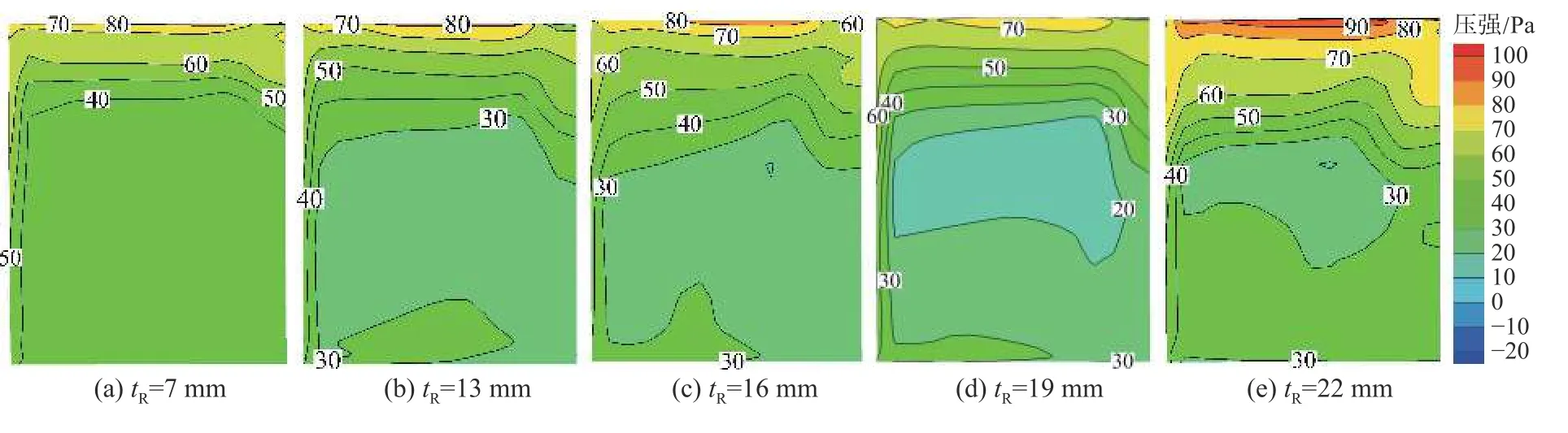
图9 呼气阶段不同厚度动叶片吸力面压力云图Fig.9 The pressure cloud map of the suction surface of the rotor blades with different thickness during the exhale stage
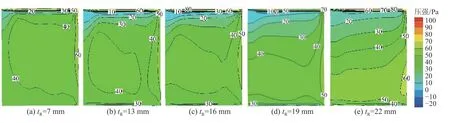
图10 呼气阶段不同厚度动叶片压力面压力云图Fig.10 The pressure cloud map of the pressure surface of the rotor blades with different thickness during the exhale stage
图11 和图12 分别为转速 ω=120 r/min 时5 种不同动叶片厚度的透平吸气阶段动叶片吸力面和压力面压力云图,气流均为自上而下。由图11 可知,在吸气阶段,动叶片吸力面沿气流方向压强分布比呼气阶段均匀;随着动叶片厚度的增大,动叶片吸力面背流侧低压区的值减小,但面积不断增大。由图12 可知,压力面中部相对高压区随着动叶片厚度的增大逐渐消失。不论是吸力面还是压力面,沿气流方向动叶片上下游压差相差较小,即转子上下游压差保持不变。

图11 吸气阶段不同厚度动叶片吸力面压力云图Fig.11 The pressure cloud map of the suction surface of the rotor blades with different thickness during the inhale stage
2.2 参量时程分析
能反映透平性能的主要物理量为动叶片输出扭矩和上下游压差,通过分析正弦气流条件下两者的变化规律,可更直观地了解动叶片厚度对透平瞬时性能的影响。
图13a 为不同动叶片厚度的透平输出扭矩时程曲线,图13b 为不同动叶片厚度的透平上下游压差时程曲线(横坐标为无量纲时间)。由图13a 结合2.1 节流场分析结果可知,当转速 ω=100 r/min 时,动叶片厚度仅对吸气阶段的输出扭矩有较大影响,两者呈正相关。在呼气阶段,动叶片流域通道宽度和吸力面曲率的增大造成了严重的流动分离,而迎流侧高速流的增长有利于正扭矩的产生,两种作用相互抵消致使输出扭矩值无明显变化;在吸气阶段,动叶片流域通道宽度的减小减弱了由吸力面曲率增大造成的流动分离,此时迎流侧高速流的增长对扭矩的有利影响起主导作用,即动叶片厚度越大,透平输出扭矩越大。由图13b 可知,在呼气阶段,随着动叶片厚度的增大,上下游压差值先减小后增大,在tR=13 mm 时透平上下游压差最小。综上可知,透平输出扭矩和上下游压差越接近峰值,动叶片厚度对其影响越大,各输出扭矩和上下游压差时程曲线之间无明显相位差。
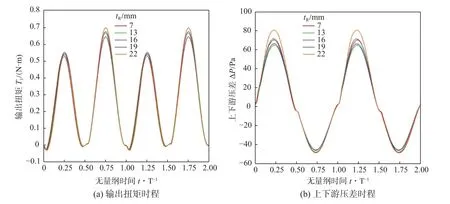
图1 3动叶片厚度对径向透平扭矩和上下游压降的影响Fig.13 The effect of the thickness of rotor blades on the torque and up-and down-stream pressure drop of radial turbine
2.3 非定常性能评价参数分析
径向透平输入系数CA、扭矩系数CT和周期平均效率 η为径向透平结构优化研究中最重要的评价指标,本节通过分析动叶片厚度tR对三者的影响,定性研究不同工作范围(不同流量系数)下透平非定常工作性能的差异。
图14 为动叶片厚度tR对径流式透平输入系数CA、扭矩系数CT和周期平均效率 η的影响。由图14a 中可知,输入系数与流量系数呈正相关,但随着流量系数的增大,输入系数的增速逐渐降低;在同一流量系数下,输入系数随动叶片厚度的增大先减小后增大,随着流量系数的增大,动叶片厚度对输入系数的影响程度逐渐增大,tR=13 mm 时的透平输入系数最小。由图14b 可知,扭矩系数和流量系数呈正线性相关;扭矩系数随动叶片厚度的增大先增大后减小,变化幅度较小,tR=19 mm 时透平的扭矩系数最大,可认为动叶片厚度对透平输出扭矩的影响较小。由图14c 可知,动叶片厚度对透平周期平均效率的影响较大,5 种透平均在流量系数Φ=1.2左右达到峰值效率;当Φ<0.4 时,动叶片厚度对输入系数、扭矩系数和周期平均效率的影响可忽略不计;而当Φ>0.4 后,动叶片厚度依旧对扭矩系数的影响较小,但对输入系数的影响逐渐增大,因此该范围内的效率随动叶片厚度的增大先增大后减小;结合式(1)和式(2)可得,tR=19 mm 的透平周期平均扭矩最大,tR=13 mm的透平上下游压差最小。综合数值计算结果,可得动叶片厚度对透平上下游压差影响较大,透平在动叶片厚度tR=13 mm 时性能最优,最大峰值效率可达47.7%。
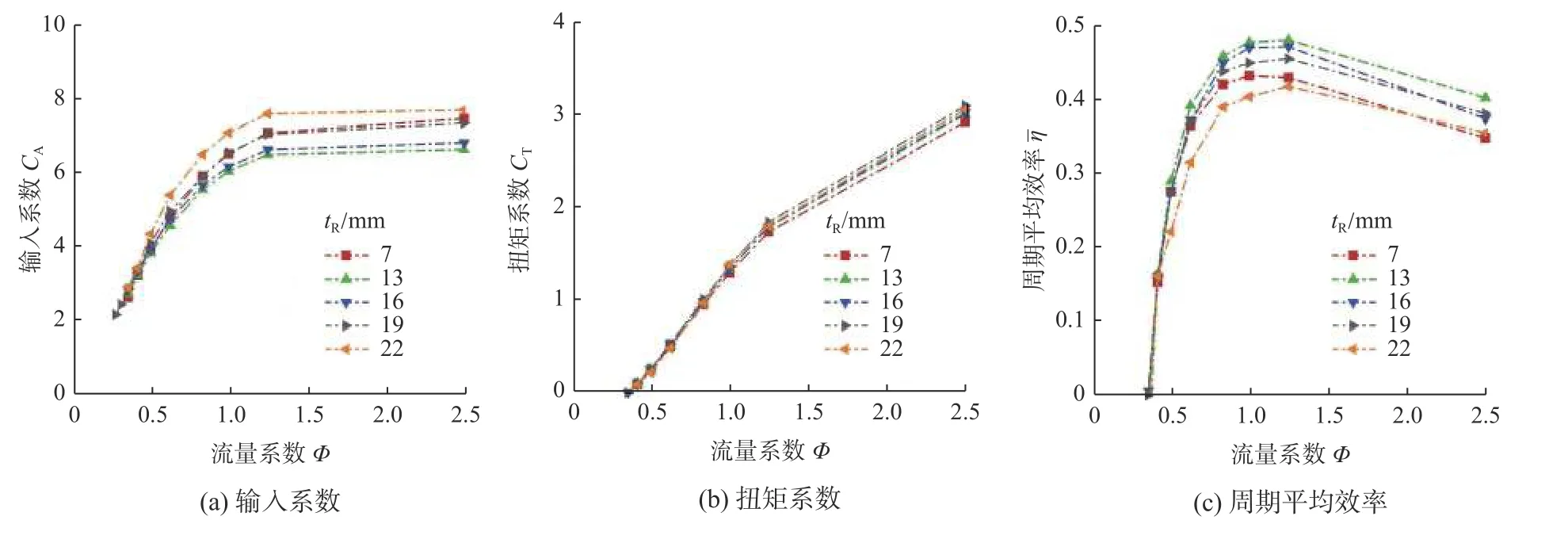
图1 4动叶片厚度对透平非定常性能评价参数的影响Fig.14 The effect of the thickness of rotor blades on the unsteady performance evaluation parameters of radial turbine
3 结论
本文构建了径向透平三维瞬态全流域数值模型,并通过与非定常试验结果对比对其进行了验证。进一步分析流场、各参量和非定常性能评价参数的变化规律,发现动叶片厚度对透平非定常工作性能有较大影响,具体结论如下。
1)径向透平不同于轴流式透平,其呼气、吸气阶段的非定常工作性能存在差异,具体表现为两阶段动叶片流域的流速、压强均存在明显差异。
2)不同厚度动叶片的叶片几何角和相对流动角的匹配程度存在差异,致使动叶片吸力面的流动分离程度也存在差异。
3)呼气阶段动叶片厚度对透平输出扭矩影响较大,两者呈正相关;动叶片厚度对上下游压差影响较小。吸气阶段动叶片厚度对上下游压差影响较大,随着动叶片厚度的增大,上下游压差先增大后减小;动叶片厚度对透平输出扭矩影响较小。
4)在不同流量系数下,动叶片厚度对透平周期平均效率的影响存在差异。当流量系数Φ>0.4 时透平周期平均效率随动叶片厚度的增加先升后降;当Φ<0.4 时两者无明显相关性。在其他结构参数保持不变的前提下,动叶片厚度tR=13 mm 时透平非定常工作性能最优,最大峰值效率为47.7%。
综上所述,合理改变径向透平冲击式动叶片吸力面的结构型式可使动叶片几何角与相对流动角相匹配,减小动叶片吸力面的流动分离,进而提高透平输出扭矩和周期平均效率。
