铁路道岔直尖轨主要组合断面打磨廓形优选研究
2022-09-28杨逸航胡伟豪肖乾
杨逸航,胡伟豪,肖乾
(1.中铁物总运维科技有限公司,北京 100036;2.华东交通大学 载运工具与装备教育部重点实验室,南昌 330013)
随着我国铁路开通运营时间的延长,线路载重逐年递增,轨道车辆通过道岔进行线路转换时轮轨间冲击作用更剧烈,导致道岔尖轨出现了鱼鳞纹、掉块、轨头踏面压宽、垂直磨耗和侧面磨耗等一系列问题[1-2].钢轨打磨作为一种最有效尖轨病害处理方法已经得到各个路局的高度关注[3].
国内外诸多学者对道岔尖轨进行研究,Schmid等[4]研究了尖轨和基本轨的不对称情况对二轴转向架通过尖轨的运行性能影响.Ghodrati等[5]对道岔尖轨进行可靠性研究,为道岔尖轨维护管理的优化提供依据.Palsson等[6]建立车辆-轨道交互的动态仿真模型,研究了铁路货车与道岔尖轨之间的动态相互作用.徐井芒[7]建立车辆-道岔耦合动力学模型对高速道岔曲尖轨磨耗仿真进行了研究.杨飞等[8]结合现场实测数据,探明了岔区钢轨磨耗的产生及发展规律,以及因磨耗引起的列车过岔动力学性能演化规律.杨逸航等[9-10]对打磨前后的高速铁路道岔打磨尖轨特征断面钢轨廓形进行测量,并建立车辆-道岔耦合动力学模型仿真模拟列车通过打磨前后道岔打磨受限区的动力学特性.
目前针对道岔尖轨主要是通过人工进行打磨[11],效率低下,打磨廓形较为单一,若按照标准道岔尖轨廓形打磨需要消耗大量人力物力[12].本文根据现场道岔尖轨实测数据,对道岔直尖轨廓形打磨工艺进行优化,优化出适合现场打磨的几组打磨廓形.
1 尖轨组合断面调查分析
1.1 现场廓形调查
对某铁路局集团有限公司管内4 249 图号道岔直尖轨主要组合断面廓形进行调查,分别为20 组合断面廓形(尖轨轨顶往下16 mm 处,宽度为20 mm位置的断面廓形)、35 组合断面廓形(尖轨轨顶往下35 mm 处,宽度为35 mm 位置的断面廓形)及50 组合断面廓形(尖轨轨顶往下50 mm 处,宽度为50 mm 位置的断面廓形),合计调查1 180 组,并将实测的廓形与全新尖轨廓形进行对比,结果如图1 所示,由于数据过多,图1 只列举了5 种实测尖轨组合断面廓形与全新尖轨组合断面廓形比较情况,分别为1#实测20、35、50 组合断面廓形、2#实测20、35、50 组合断面廓形、3#实测20、35、50 组合断面廓形、4#实测20、35、50 组合断面廓形、5#实测20、35、50 组合断面廓形,通过将实测组合断面廓形与全新组合断面廓形轨腰对齐,对比轨头廓形可知,二者廓形偏差较大,若完全依照全新尖轨断面廓形进行打磨,打磨难以执行,故需对打磨廓形进行优化.

图1 不同组合断面廓形对比分析Fig.1 Comparative analysis of profiles with different sections combination
1.2 打磨廓形断面区域划分
以20 组合断面廓形为例,将20 断面轨顶最高处往下移动16 mm做一条平行于X轴的直线,直线与20组合断面廓形左右两端相交,过此条直线,作5 条平行于Y轴的直线,将直线平均分为6 段,20 组合断面廓形划分为6个区域,如图2所示.其中,1区域范围为[0,15.2]、2 区域范围为[15.2,30.4]、3 区域为[30.4,45.6]、4 区域为[45.6,60.8]、5 区域为[60.8,76]、6 区域为[76,91].1区域为非轮轨接触区域,其廓形变化对轮轨接触、尖轨使用寿命以及打磨量等关键因素没有影响,故对此区域不进行设计,保持原有廓形.
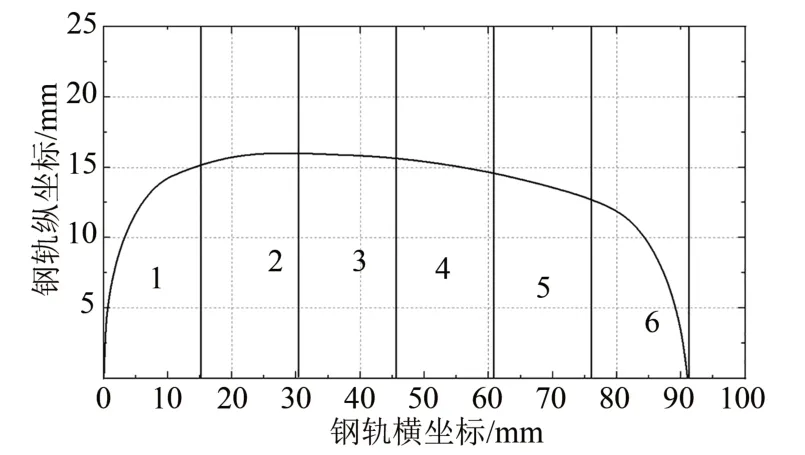
图2 20 组合断面廓形区域划分Fig.2 Area division of 20-section combination profile
将调查1 180 组中20 组合断面廓形与全新20 组合断面廓形轨腰处对齐,将实测的所有20 组合断面廓形进行离散化处理,并对2~6 区域单独进行正态分布检验,校验得到20 组合断面2~6 区域内各点分布满足正态分布规律,各区间浮动范围如图3 所示.

图3 20 组合断面廓形各区域范围Fig.3 Scope of each area in 20-section combination profile
2 尖轨廓形优化
2.1 算术平均法各区域拟合
计算得到20 组合断面廓形2~6 区域浮动范围后,平行于X轴,将每个区域横向均分为10 个区域,并使用算术平均法对每份总离散数据选择代表点.
算术平均法[13]是指依次计算离散点在各个位置的平均值,采用算术平均法得到的代表点位置坐标为(xi,yi)为

式中:z为每区域测量廓形离散点总数;(xij,yij)为第j条廓形曲线在i位置上坐标;(xi,yi)为代表点在i位置坐标.
2.2 多段曲线多项式整体拟合
道岔尖轨组合断面廓形曲线得到的是N+1 个互相离散的点,xi处的函数值f(x)无法确定,因此需要通过曲线拟合来确定一个拟合函数G(x),用拟合函数G(x)来描述xi和对应函数值f(x)之间的关系[14].
设拟合函数是一个n次多项式为

其中β为系数,同时假设
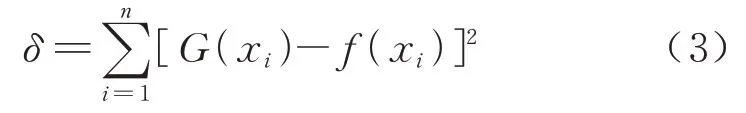
式中:δ为拟合函数和真实值之间的偏差平方和,确定式(2)的系数β,使得偏差平方和最小

根据图3 将钢轨廓形分为以上6 个区间,取区间内5 个线段.对于分段曲线数据点有限时,三阶多项式拟合能更好地满足拟合曲线的精度要求,对各个分段内的数据分别进行三阶最小二乘多项式拟合,分别将数据带入式(5),可求得各段曲线的拟合系数ai,bi,ci,di.
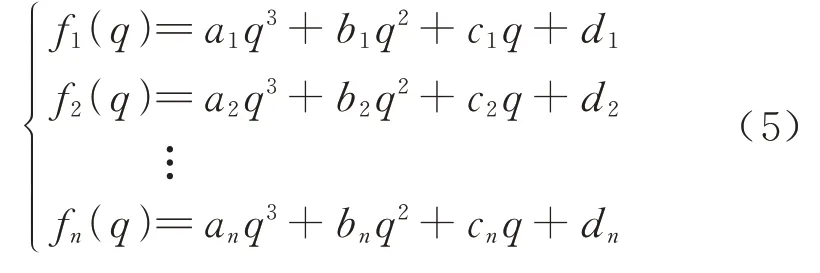
由于式(5)各分段拟合曲线相交得到的分段点,很难保证曲线在各个分段点处拟合曲线连续可导,于是采用插值拟合[15]方法将每段曲线连接.
由于道岔廓形曲线是一个连续的光滑曲线,对各个连接插值曲线函数增加约束条件,使得连接插值曲线Ti(x)和各个分段拟合曲线函数在连接点(xik,f(xik))和(x(i+1)(k+1),f(x(i+1)(k+1)))的函数值相等,约束条件为
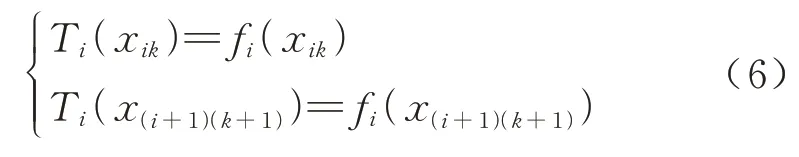
同时保证插值连接曲线和各个分段函数(xik,f(xik)) 和(x(i+1)(k+1),f(x(i+1)(k+1))) 的导数相等,约束条件为
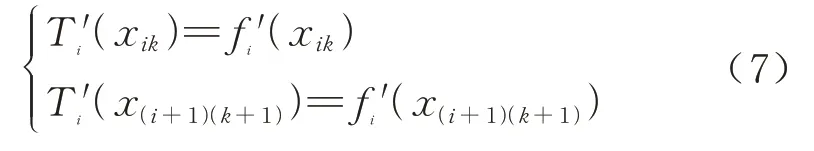
同时插值连接曲线时保证道岔曲线在设计过程中分段点位置连续可导,因此插值连接曲线采用三阶插值可以满足
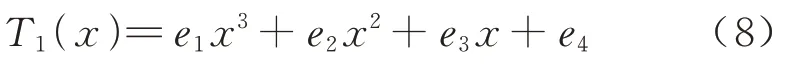
式中:e1、e2、e3、e4为系数,结合式(5)及式(8)可以得到式(9),从而得到钢轨廓形拟合结果.

2.3 优化廓形几何特性分析
将所测得的20 组合断面钢轨廓形竖向分成6 个大区域,随后对各区域的垂向偏差值进行归一化分析,由正态分布理论得到道岔关键断面偏差范围.然后对6 个大区域中每个区域横向进一步均分成10 个小区域,基于算术平均法对每个区域进行代表点选取,通过多段多项式拟合算法对多个曲线进行拟合,最终设计得到20 组合断面10 组道岔尖轨打磨优选廓形,如图4(a)所示,35 组合断面廓形及50 组合断面廓形优化思路与20 组合断面廓形一致,钢轨内侧轨距角由低到高依次命名为1#~10#钢轨尖轨组合断面廓形,优化后尖轨组合断面廓形不考虑尖轨和基本轨之间的间隙,如图4 所示.
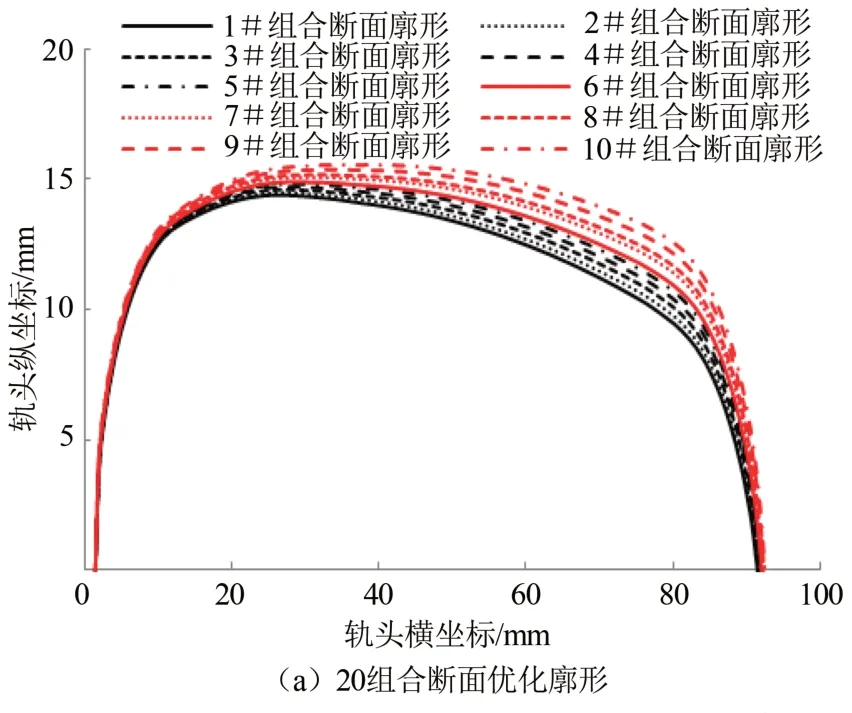
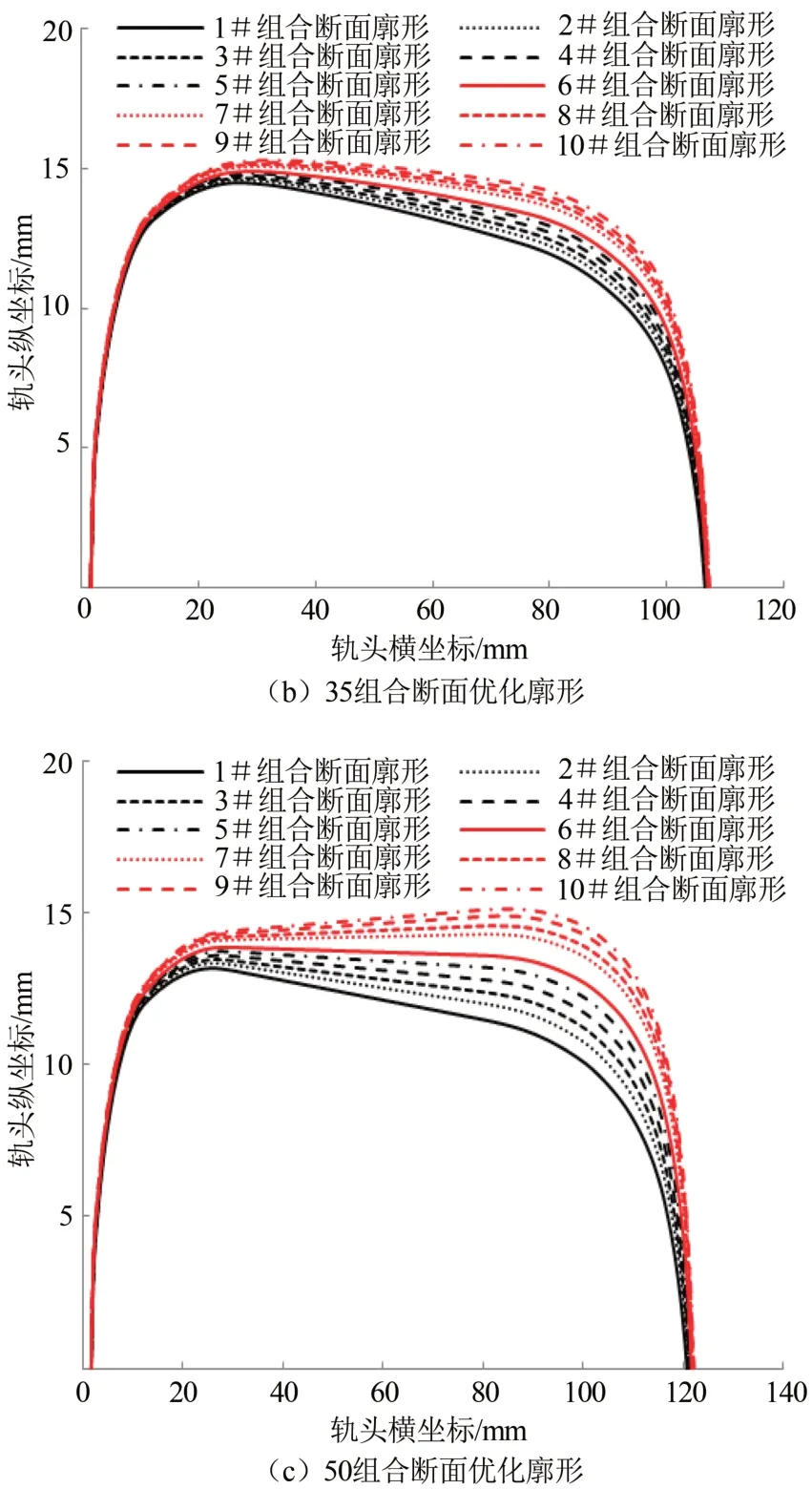
图4 各个组合断面优化廓形Fig.4 Optimized profile with different section combinations
对4249 图号道岔全新尖轨组合断面廓形及优化后尖轨组合断面廓形与全新车轮进行匹配计算,轮轨接触等效锥度变化如图5 所示,由图5 可知,随着横移量的增加,优化后尖轨组合断面廓形与全新车轮进行匹配未出现等效锥度突变现象,轮轨接触关系理想[16-17].

图5 各组合断面廓形等效锥度变化Fig.5 Equivalent conicity variation of optimized profile with different section combinations

3 动力学仿真特性分析
3.1 动力学模型建立
在动力学UM 软件中建立车辆精细模型[18].考虑车体转向架横向、竖向、侧滚、点头、摇头运动以及轮对横向、竖向、侧滚、摇头运动,包括1 个车体、2 个构架、4 条轮对和8 个轴箱总计15 个刚体.其中,车体、构架、轮对各有6 个自由度,轴箱相对轮对有1 个转动自由度,共有50 个自由度.模型充分考虑非线性轮轨接触几何关系、非线性轮轨蠕滑特性及非线性车辆悬挂系统.减振器力元模型选用考虑节点刚度的Ruzicka 模型,并考虑抗蛇行减振器的非线性特性.二系空气弹簧分别采用线性弹簧力元模拟,同时考虑阻尼性质.转臂节点采用特殊力元模拟.建模过程中充分考虑轮轨接触几何,横向止档,悬挂力元等非线性特性,具体模型参数如表1 所示.

表1 车辆动力学部分参数Tab.1 Some vehicle dynamic parameters
车轮踏面类型为全新廓形,采用轮轨非椭圆多点接触算法计算蠕滑力,道岔直尖轨廓形使用全新尖轨组合断面及1#~10#组合断面设计廓形,建立得到车辆-道岔耦合系统动力分析模型如图6所示.

图6 车辆-道岔耦合系统动力分析模型Fig.6 Dynamic analysis model of vehicle-switch coupling system
3.2 轮轨接触磨耗特性
对比列车通过全新尖轨组合断面及不同组合断面设计廓形磨耗特性如表2 所示,列车依次通过全新20 组合断面、全新35 组合断面、全新50 组合断面时轮轨接触磨耗功峰值最大,为3 014.48 W,列车依次通过1#20 组合断面、10#35 组合断面、1#50 组合断面时轮轨接触磨耗功峰值最小,为1 228.04.故列车通过不同组合断面设计廓形磨耗功峰值较为理想,未出现轮轨磨耗较大情况.
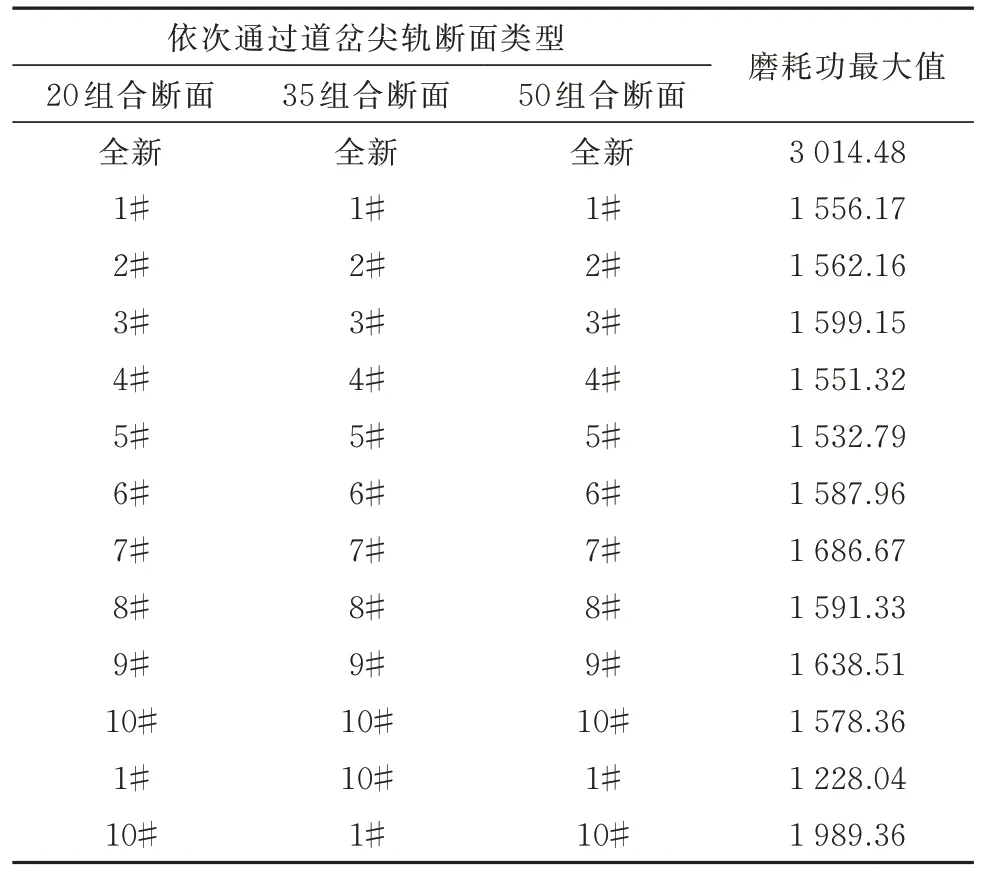
表2 列车通过尖轨轮轨接触磨耗功Tab.2 Wheel-rail contact wear work of vehicle through rail switch W
3.3 转向机构架横向振动特性
对比列车通过全新尖轨组合断面及不同组合断面设计廓形横向振动特性如表3 所示,列车通过依次通过由全新20 组合断面、全新35 组合断面、全新50 组合断面拟合得到的直尖轨时转向架构架横向加速度最大值最大,为13.99 m/s2;列车通过依次通过1#20 组合断面、10#35 组合断面、1#50 组合断面拟合得到的直尖轨时转向架构架横向加速度最大值最小,为10.91 m/s2.同时,列车通过依次通过全新20 组合断面、全新35 组合断面、全新50 组合断面拟合得到的直尖轨时转向架构架横向加速度均方根值最大,为47.79;列车通过依次通过1#20 组合断面、10#35 组合断面、1#50 组合断面拟合得到的直尖轨时转向架构架横向加速度均方根值最小,为30.88.故列车通过不同组合断面设计廓形转向架构架横向加速度最大值及均方根值均较为理想,列车横向振动特性较好.
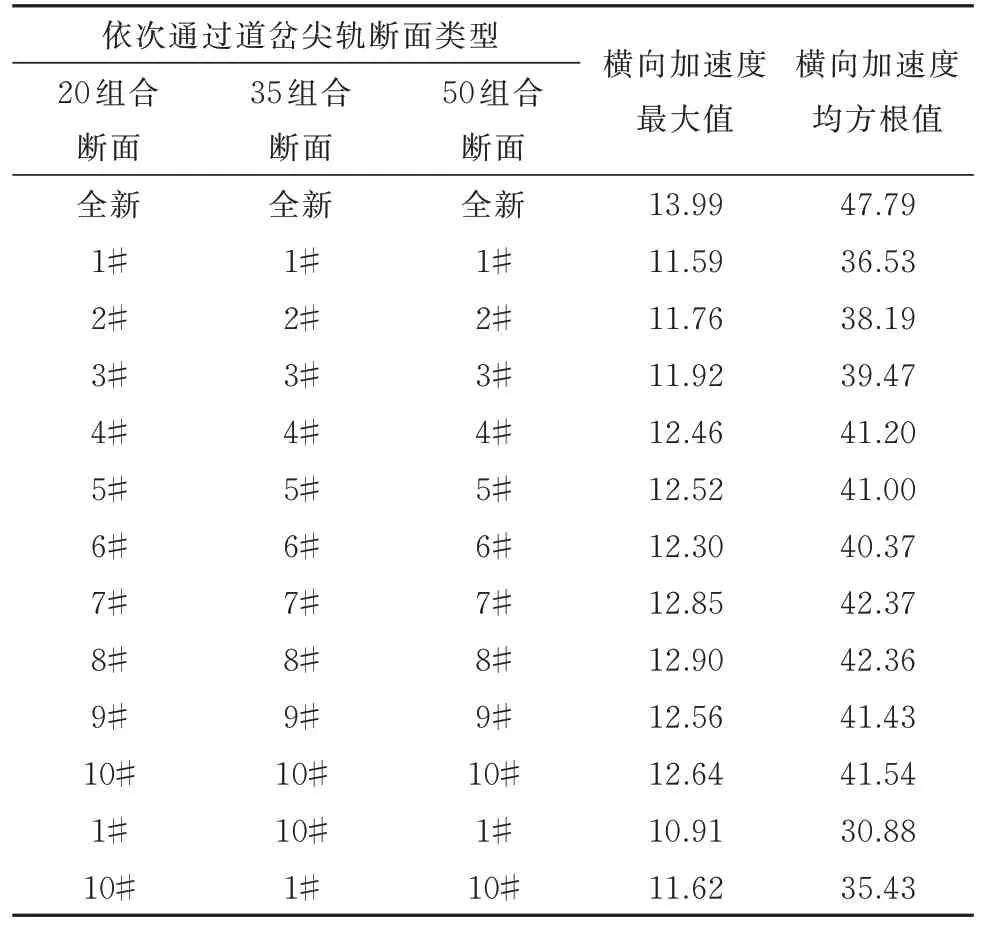
表3 列车通过尖轨构架横向加速度Tab.3 Transverse acceleration of the vehicle through rail switch m/s2
3.4 转向机构架垂向振动特性
对比列车通过全新尖轨组合断面及不同组合断面设计廓形垂向振动特性如表4 所示,列车依次通过10#20 组合断面、1#35 组合断面、10#50 组合断面拟合得到的直尖轨时转向架构架垂向加速度最大值最大,为0.89 m/s2;列车依次通过1#20 组合断面、10#35 组合断面、1#50 组合断面拟合得到的直尖轨时转向架构架横向加速度最大值最小,为0.68m/s2.同时,列车通过依次通过1#20 组合断面、1#35 组合断面、1#50 组合断面拟合得到的直尖轨时转向架构架横向加速度均方根值最大,为0.27;列车通过依次通过全新20 组合断面、全新35 组合断面、全新50 组合断面拟合得到的直尖轨时转向架构架垂向加速度均方根值最小,为0.16.故列车通过不同组合断面设计廓形转向架构架垂向加速度最大值及均方根值均较为理想,列车垂向振动特性较好.

表4 列车通过尖轨构架垂向加速度Tab.4 Vertical acceleration of the vehicle through rail switch m/s2
4 现场打磨试验
对某铁路局集团有限公司管内4个站道岔使用尖轨组合断面优化廓形进行打磨,若按照尖轨组合断面全新廓形进行打磨,每2 个天窗才能打磨一组尖轨,但依照尖轨组合断面优化廓形进行打磨,每个天窗能完成2 组道岔打磨,打磨效率提高4 倍,打磨后轨面状态较好,轨面未有掉块及裂纹,如图7 所示.对打磨前后线4个站道岔轨检车数据分析,结果见表5,由表5可知,打磨前横向及垂向加速度均值分别为1.59g、0.56g,打磨后横向及垂向加速度均值较打磨前分别降低4.40%、5.36%,为1.52g、0.53g,表明通过廓形轨检车平稳性得到提升,且与动力学仿真计算结果变化趋势一致,证明动力学仿真模型建立较为准确.
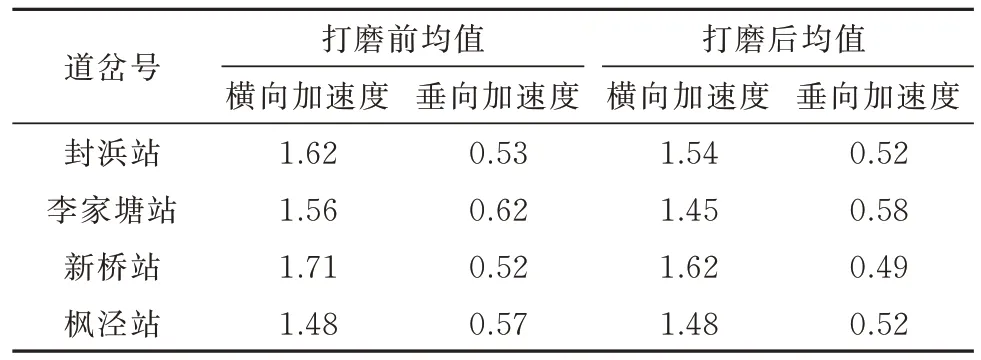
表5 动检车打磨前后动态数据变化Tab.5 Dynamic data variation before and after grinding of inspection car g

图7 打磨后封浜站下行28 号道岔尖轨轨面状态Fig.7 Rail surface state after grinding of No.28 rail switch at Fengbang station
5 小结
1)通过分析轮轨几何接触特性可知:随着轮对横移量的增加,优化后尖轨组合断面廓形与全新车轮进行匹配未出现等效锥度突变现象,轮轨接触关系理想.
2)基于车辆-道岔耦合系统动力分析模型,仿真模拟列车通过10 组道岔尖轨主要断面优化廓形动力学特性可知,列车通过尖轨打磨组合断面优化廓形磨耗特性及列车横向运行稳定性优于列车通过尖轨全新组合廓形.
3)通过现场打磨试验结果分析可知:使用尖轨断面优化廓形打磨效率高,打磨后轨面状态较好,轨面未有掉块及裂纹,打磨后轨检车横向及垂向加速度较打磨前均有改善,轨检车平稳性得到提升.
