关于核心素养下的高职数学关键能力评价探索*

潘蕊 王洋

（四川交通职业技术学院 四川成都 611130）

一、基于数学核心素养的评价模型的设计目的

在2014年发布的《教育部关于全面深化课程改革、落实立德树人根本任务的意见》中明确提出，要进一步明确各学段各自教育功能定位，理顺各学段育人目标。2017年发布的高中阶段（含中职、普高）全国《数学课程标准》已明确数学核心素养概念，将“学科核心素养”与“课程目标”整合，作为《课标》的六大部分之一。因此，职业教育阶段明确核心素养培养已是必然趋势。基于此，新时代的高职数学教育改革需顺应“学科核心素养培养+职业关键能力发展”双线融合的改革趋势。数学课程作为高职院校开设最广泛的公共基础课程之一，不仅承载着落实“立德树人”的根本任务及培育学生数学核心素养的基本功能，也承担了一定的职业素养培养的责任。

目前，大部分高职数学课程的考核形式仍强调终结性考试并辅以平时作业、考勤等等。考试内容更多偏向于对概念理解、计算方法使用等方面。教学目标方面，大部分仍采用“知识、能力、情感”三维教学目标。在学业评价上，大部分的评价内容以知识掌握本身为主，缺乏一个评价框架来对学生核心素养各方面进行记录、考察及分析。

二、“学科+职业”的素养成分及结构

针对高职院校特点来说，学生在动手操作模式的学习能力上普遍高于理论模式的学习能力，高职数学的培养更多的是在实践中逐渐形成的数学关键能力、数学情感态度价值观及基本的品格。这就要求教学中不仅仅关注学生具体知识的掌握及应用，更应关注学生在具体职业情境中对数学知识的理解、应用及操作。学生通过数学学习，能够具备透过相关职业情境观察数学的能力；能够通过正确的数学观来看待相关的职业现象，从而进一步利用数学解决现实职业问题。也就是说，高职数学教育的素养培养具备了“数学核心素养+职业核心素养”的双线融合特点。

1.关于数学核心素养

数学核心素养分为两个部分：学科核心素养（关键能力）、品格与价值观。2017年颁发的《普通高中数学课程标准》明确了数学学科核心素养的六个方面，《课标》中素养的六个成分也就是六种数学关键能力，而这六个关键能力之间的关系可用下图表示[1]：

图1 数学关键能力成分与结构

在这六种关键能力中，逻辑推理和直观想象是既相互独立又相互关联的两种基础能力，是另外四种能力的基础。数学运算与数学抽象既是关键能力也具备生成剩余两个关键能力的中介特质。数学建模和数据分析是综合性最强的两种关键能力，也是与核心素养中的实践创新最接近的能力。

品格与价值观方面，喻平指出，数学核心素养中的品格与价值观的指标分为：数学学习态度、数学思维品格、学会数学学习、数学价值观念[1]。

2.关于职业核心素养

关于我国的职业核心素养，笔者认为，同样包含了能够适应终身发展和社会发展需要的通用关键能力及必备品格。这种素养超越了传统职业教育原有的知识和能力结构。其中职业关键能力是一种共性专业素养，其与具体工作岗位技能不直接相关，是一种能在不同情境和职责情况下作出正确判断及选择的通用能力，更是一种能应对职业生涯中各种不可预见变化的能力。而职业必备品格则是指在任何职业情境下都必须遵守的职业道德、行业规范、职业精神等[2][3]。

结合职业院校特点，通过对相关文献的检索和专家咨询，笔者整理出了在数学教育过程中所涉及的职业核心素养成分及结构。（如表1所示）

表1 职业核心素养指标划分

3.结合核心素养的职业院校数学教育素养的关键能力评价指标及水平

笔者在上述对数学核心素养与职业核心素养的探究中发现，数学学科关键能力重点在知识获取与应用，职业核心素养的通用关键能力重点在技能获得与操作。它们既是两种并行的能力培养，同时又具有承继关系。面对将来会进入各技能行业的学生，高职院校数学教育既与高中阶段《课标》有着相同的数学核心素养培养目的，也需将职业核心素养的培养纳入数学教育目标中。数学关键能力培养为“根”，结合职业情境的关键能力培养为“叶”。在培养数学学科关键能力的目标上，高职数学教育更应进一步升华，完成辅助职业教育的使命。这两项育人目的的有机融合，能够更好地把学生培养成符合新时代要求的全面发展的职业技能型人才。

从知识内容来看，六个学科关键能力之间呈现出明显的层次递进关系，四个职业关键能力之间则属于并列关系。各学科关键能力的培养过程中可能会包含多种职业关键能力元素，具有明显的交集。比如，数学建模与数据分析能力包含职业关键能力中的各项二级能力。从知识水平划分来看，在数学教育中体现的职业通用能力大部分被认为是较高级认知水平，更多地体现在知识迁移和知识创新中。因此，高职数学教育中的职业核心素养培养可融入进数学学科核心素养中，在具体知识内容中进一步呈现。

在高中阶段的数学核心素养关键能力评价体系中，各关键能力的水平划分为三个等级：知识理解、知识迁移与知识创新[1]。进一步结合职业核心素养指标内容特点，笔者针对高职数学课程内容及特点，设计了如下的关键能力评价水平框架。（如表2所示）

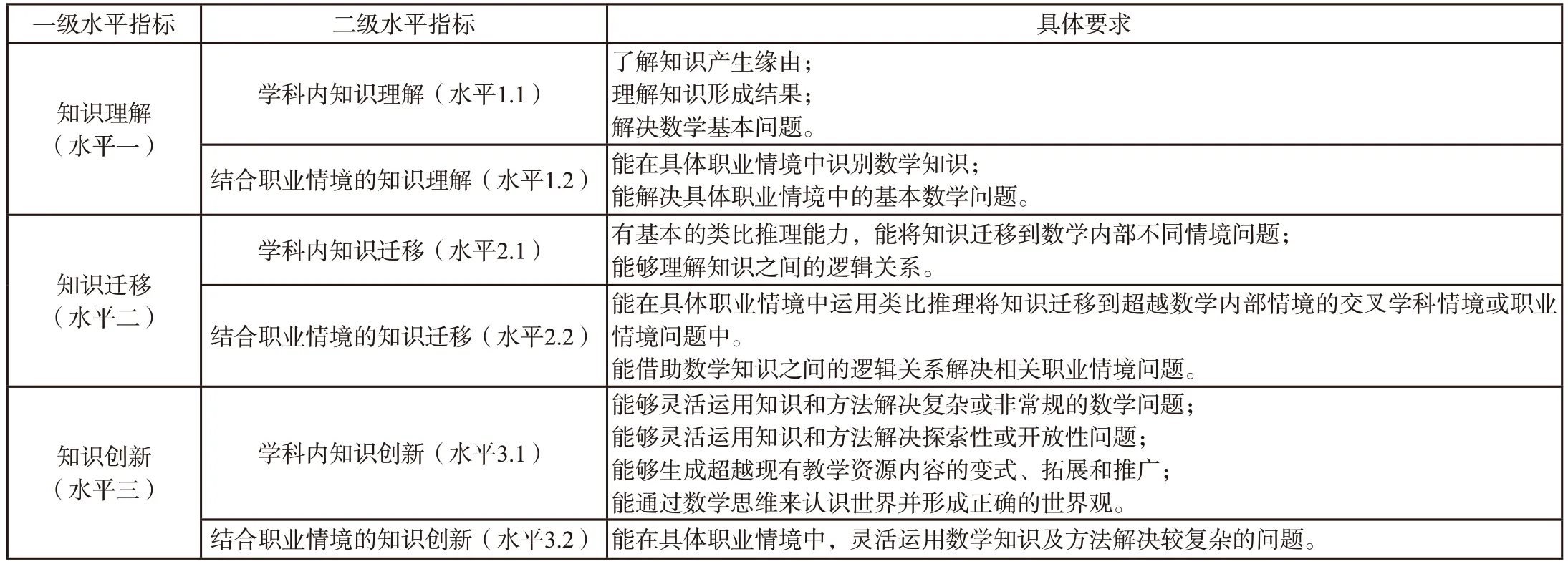
表2 关键能力评价的水平划分

三、基于核心素养评价指标的测试题编制——以某交通类专业的“导数及其应用”为例

测试题的编制，参照上述关键能力水平内容及等级划分，可利用水平等级为“经”、知识内容为“纬”的模式来构建二维评价框架。

笔者以本文中的评价指标结构为框架，对《高等数学》第二模块“导数及其应用”内容进行试题编制。该部分内容在整个课程知识体系中起承上启下的作用，重点在对导数概念的理解、基本计算方法的运用。从学科素养层面来看，集中在逻辑推理、数学运算及数学抽象三个方面，其中会涉及到少量数学建模内容。从职业素养层面来看，导数运算在工程测量方面具有广泛应用。学生学习完该部分知识内容后，应该能理解导数概念并能进行基本计算。通过该部分内容的学习，学生应该能在具体工作情境下，通过对导数概念的理解，有效识别弧微分、曲率的概念及特点，并且能接受其在多种情境中的具体作用。在此基础上，还能利用导数计算，正确计算出物件的曲率，最终判断或比较物件的弯曲程度。

基于上述分析，笔者对该部分内容编制了测试题，并在XX学院某交通类专业2020级274名学生中进行了预测试。测试卷总共回收274份，通过SPSS进行了统计分析。通过分析结果对测试题目进行了删减，最终保留8个题目。最终统计结果显示：KMO值为0.316＜0.5，因此8个变量间相关程度不高；且所有题项与总测验得分在0.001的显著水平下相关。因此，每个题项与测验卷的测验目标一致。综上，说明因子选取合理，保留所有题项。下图展示了基于核心素养的“导数及其应用”关键能力学业评价模型的二维评价框架。

图2 交通类专业基于核心素养的“导数及其应用”关键能力学业评价模型

结语

在国家大力提倡“立德树人”教育方针的背景下，高职院校数学教育改革应积极加入此浪潮。学习和研究核心素养下的育人机制及评价指标是高职数学教育“立德树人”教育改革中的必要一环。在完善的育人机制及合理的评价指标下，方可做到有理可寻、有标可追。

笔者目前仅对核心素养中的关键能力学业评价指标进行了初探，而核心素养不仅仅包含关键能力，更有品格与价值观，这样方可做到培养全面发展的人。同时，随着职业教育改革的大力发展，面向高职院校学生的数学教育形式应更加丰富、内容应更具特色。因此，核心素养的考察形式不应仅仅局限于考试，还应融入到教学活动各环节，如结合定性与定量考核、平衡过程性与终结性考核、加入互评环节等等。

核心素养的培养超越了学科的界限，让高职院校学生的数学学习更加生动、更具职业特色。因此，结合核心素养培养的高职数学教育能使得学生能够更好地适应未来职业生涯发展。