非矩形像素金属网格触控屏上莫尔纹的仿真和分析

桑胜田，苏渝阳，夏磊，于涛，王治乐

（哈尔滨工业大学 航天学院，黑龙江 哈尔滨150080）

1 引 言

随着显示技术的发展和智能终端的普及，触控设备的使用越来越普遍［1］。在触控屏显示技术中，由于触控板和显示器的叠加而引起的莫尔纹问题一直是近年来研究的热点［2-3］。在触控显示技术的发展过程中，由于过去主流触控产品所使用的氧化铟锡材料不可再生，新兴的金属网格触控显示屏逐渐成为了主流［4］。金属网格触控屏使用金属网格作为触控板的材料，设计和制造都相对容易［5］。

有关莫尔现象的研究分布在物理与显示等诸多领域［6-7］，与显示技术相关的莫尔纹研究兴起于21世纪初。2009年，Byung等利用图像处理技术研究了液晶显示器（LCD）上出现的莫尔纹问题［8］。2014年，Seok等提出了一种仿真和分析显示系统中莫尔纹问题的算法，这种算法通过计算各个光学传输层透过率函数的乘积与点扩散函数的卷积来仿真莫尔纹。相比于光线追迹的方法，这种方法运算速度更快，但是不能处理有复杂结构的光学层存在的情况［3］。在本文的研究中，金属网格的线宽只有4 μm，而间距却有200 μm左右，只能用矩形函数来表达，利用这种方法复杂度较高，运算非常耗时。2015年，Chen等利用空间频率的概念研究了金属网格触控屏上的莫尔纹问题，这种方法能够用来判断莫尔纹的空间周期，但是无法仿真莫尔纹的图案［9］。2016年，Pournoury等人利用人眼对比度函数（CSF）作为空间滤波器分析了金属网格触控屏上莫尔纹的可见度，并用仿真图案的标准差大小作为评判莫尔纹可见度的指标［10］。这种方法把显示器子像素近似为矩形来处理，无法处理非矩形子像素的情况。2018年，京东方公司的Xie等人利用惠更斯菲涅尔衍射原理来仿真和分析金属网格触控屏上出现的莫尔纹，并指出图案对比度越大，空间频率越低，莫尔纹可见度越高［11］。同年，Victor等提出利用优化金属网格的参数（网格夹角和间距）的方式来降低莫尔纹的可见度并筛选出可见度最低的网格参数，这种方法同样是把子像素近似为矩形来处理［12］。

在之前的研究中，我们提出了利用计算显示平面子像素受金属网格遮挡后的透过率矩阵来仿真金属网格触控屏上莫尔纹的方法，同样也是把子像素看作矩形［13］。当子像素形状与矩形差异较大时，利用近似为矩形来处理的方法会带来较大的误差。为了提高仿真分析的精度和算法的可靠性，本文基于我们之前的工作，研究了子像素不可近似为矩形时金属网格触控屏上的莫尔纹的仿真算法和可见度量化分类方法。

2 莫尔纹的仿真

国内外相关的研究人员已经研究出了多种显示屏上莫尔纹的仿真方法，常用的有基于透过率计算的仿真方法［1，13］、光线追迹法［14-15］和衍射积分法［11，16-17］等。光线追迹法利用追踪光线在显示器各层的传播情况来仿真莫尔纹图案；基尔霍夫衍射积分法和菲涅尔衍射积分法均把像素平面和触控层看作叠加起来的单层衍射屏来计算衍射后的光强分布；基于透过率计算的仿真方法则不考虑光的衍射，把像素平面和触控层中透光的部分看作透过率为1，不透光的部分看作透过率为0，通过计算子像素的透过率来仿真莫尔纹图案。本文选用处理简单且具有较高运算效率的基于透过率计算的仿真方法来进行仿真和分析，通过计算机模拟生成非矩形子像素受金属网格遮挡的图像并扫描像素点来计算子像素的透过率矩阵，从而得到仿真莫尔纹图案，并据此在频域进行分析判断莫尔纹的可见度。

如图1所示，1个像素由3个子像素——红色滤光片（RCF）、绿色滤光片（GCF）和蓝色滤光片（BCF）组成，图1（c）、（d）为示意图（a）、（b）对应的实物显微镜照片，图1（c）为子像素形状可近似为矩形的液晶显示器像素平面的代表性照片，图1（d）为子像素形状为非矩形的液晶显示器像素平面的代表性照片。液晶显示器的子像素形状除了这两种之外还有斜矩形形状，本文只针对图1（b）所示形状的非矩形子像素金属网格触控屏进行研究。

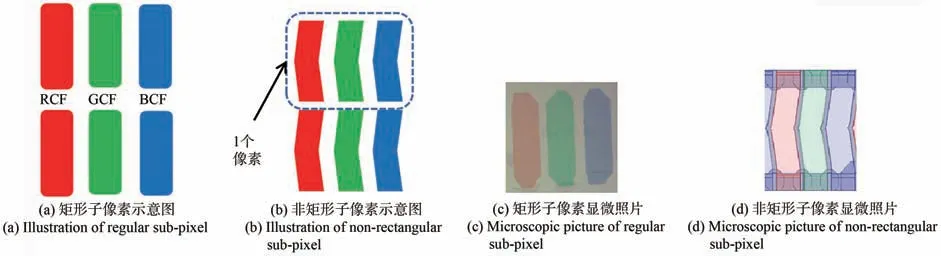
图1 子像素为非矩形的液晶显示屏Fig.1 LCD with non-rectangular sub-pixels

2.1 非矩形子像素图案的生成

非矩形子像素的形状虽然不是矩形，但是它们组成的像素平面也是周期性图形，利用计算机生成单个周期的图形，然后按周期重复就可以模拟生成像素平面的图案。在利用计算机生成如图1（b）所示的单个周期图形的时候所需的参数和步骤如图2所示。①表示旋转操作，②表示剪切操作，③表示对称复制操作，④表示拼接操作。

图2 仿真所需的参数和图形生成步骤Fig.2 Parameters for moire pattern simulation and the procedure for graph generating

在生成图1（b）所示形状的子像素时，先生成一个矩形形状的子像素，然后利用旋转矩阵得到旋转后的矩形子像素，再进行剪切，将剪切得到的图形进行竖直翻转并拼接就得到了最终的图形。上述过程如图2（b）所示，使用到的旋转矩阵为：

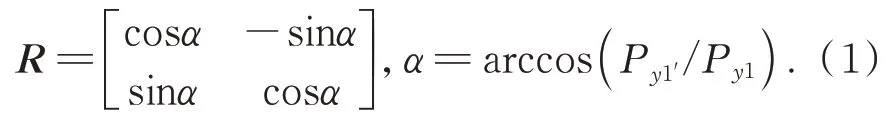
2.2 透过率矩阵的计算

在金属网格触控屏上，像素平面与金属网格平面叠加（网格放置在上层）会导致子像素受到遮挡，透过率会降低，遮挡严重且形成周期性图案会产生人眼可见的莫尔纹，本文通过计算受遮挡像素的透过率来模拟莫尔纹。子像素的透过率用式（2）计算［13］：

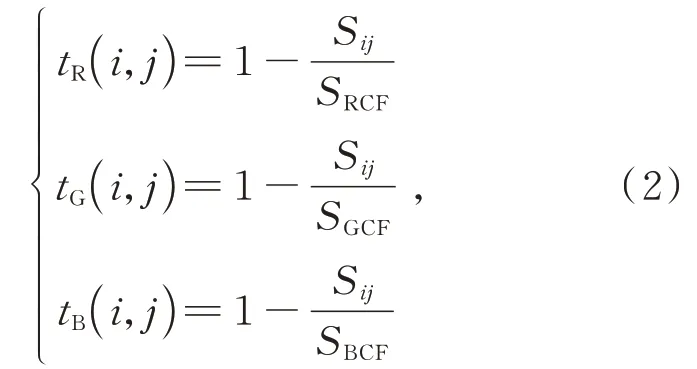
其中Si，j是第i行j列子像素受金属网格遮挡的面积，SGCF、SRCF和SBCF分别是GCF、RCF和BCF的面积，tR(i，j)、tG(i，j)和tB(i，j)表示GCF、RCF和BCF的透过率。子像素透过率计算的方法如图3所示。本文中计算透过率时考虑的是正视的情况，由于在实际的金属网格触控屏中金属网格层与液晶显示器像素平面之间存在约200 μm的间隔，当以一定角度斜视时，金属网格相对像素平面的遮挡情况与正视时会有轻微位移，位移的大小视具体显示器的参数和斜视角度不同大约在100 μm，对莫尔纹图案的影响通常较小。

图3 子像素透过率矩阵的计算示意图。（a）非矩形像素平面示意图；（b）金属网格参数示意图；（c），（d）像素平面的叠加示意图；（e）子像素透过率矩阵示意图。Fig.3 Schematic for the calculation procedure of sub-pixel transmittance matrix.（a）Illustration of black matrix for non-rectangular pixel；（b）Illustration of metal mesh parameters；（c），（d）Illustration of the superposition for pixel plane；（e）Transmittance matrix schematic for non-rectangular sub-pixel.

仿真时金属网格的参数为夹角θ和周期T（图3（b）），网格线宽为4 μm。在得到如图3（e）所示的透过率矩阵后，将透过率等比例放缩到0～255用来控制电脑显示器像素值就可以仿真莫尔纹。因人眼对绿色最为敏感，故仿真绿色图片进行分析。仿真绿色图案时，只需计算由tG(i，j)组成的透过率矩阵。利用此方法仿真得到的莫尔纹图片如图4所示。θ表示金属网格的夹角，T表示金属网格的周期。仿真时使用的液晶显示屏参数为：Px=Py=100 μm，Py1=Py2=42 μm，Py1'=Py2'=42 μm，Dx=30 μm。

图4 莫尔纹仿真图片Fig.4 Simulated moire patterns

3 莫尔纹可见度的预测方法

在实际观测实验中，被观测员判定为高可见度的莫尔纹图案具有空间周期大且对比度较高的特征。在频谱图中，空间频率的大小和幅值分别能反映空间周期和对比度，因此可以从频域来分析莫尔纹的可见度。本文首先对仿真得到的莫尔纹图案进行二维傅里叶变换，然后进行频域滤波，提取特征频率fe作为莫尔纹可见度评判的参考指标。在进行莫尔纹可见度的分类时，引入由观察员给出的判断频率作为基准，分类方法如式（3）所示：

其中，JR为分类结果，判断频率为2 lp·mm-1；OK表示莫尔纹可见度较低，达到可用的程度；NG表示莫尔纹的可见度较高，观察员认为会影响视觉体验，为不可用的程度。判断频率的值一般根据显示器像素尺寸的不同取值范围为1.7～2 lp·mm-1之间，显示器像素尺寸越小，判断频率越高。由于实际生产时只关心匹配的触控屏是否可用（即莫尔纹的可见度是否足够轻微），匹配结果只有OK和NG两种。通过频谱分析发现，在低频区出现的高幅值频率分量对莫尔纹的可见度影响较大，可以利用一个特征频率来反应莫尔纹的可见度。为了综合考虑高幅值频率分量对莫尔纹可见度的影响，本文中特征频率取为低频区（空间频率小于3 lp·mm-1）幅值最大的频率fm和幅值次大的频率fsm中的小值。利用快速傅里叶变换得到的空间频谱中高频区、0频分量和杂频会干扰特征频率的提取，因此需要进行低通滤波、去0频和去杂频的滤波操作，滤波流程如图5所示。这里使用的低通滤波器截止频率为3 lp·mm-1，去杂频时使用一个3×3的滤波器进行领域滤波，滤波器输出频率fo为：

图5 特征频率的提取Fig.5 Extraction procedure of characteristic frequency

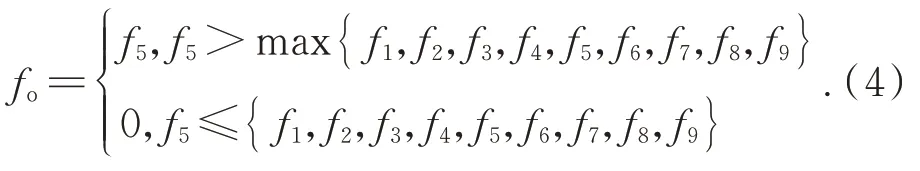
4 实验结果及分析

实验用的显示器参数如表1所示。采用将子像素近似为矩形的算法（下文均简称为原算法）进行仿真时，显示器的参数只有Px、Py、Dx和Dy四个。实物匹配结果和前后两种算法的仿真结果如图6～8所示，图中的T（单位为5 μm）表示金属网格的周期，θ（单位为（°））表示网格的夹角。金属网格的角度参数范围为25°～38°，步长为1°；金属网格的周期范围为30～52，步长为1。图6所示的实物匹配结果是由观察员在距离显示屏25 cm处观察得到的。图7、8中的数值为反应莫尔纹可见度的特征频率fe（单位为l p·mm-1），颜色由红到绿表示特征频率由低到高。因为空间周期的大小与空间频率的数值成反比关系，故特征频率越高表示莫尔纹可见度越低，用绿色表示；特征频率越低表示莫尔纹可见度越高，用红色或者橙黄色表示。图中用渐变色来反应莫尔纹可见度的变化趋势，方便对实验数据进行分析。

表1 实验用显示器的参数Tab.1 Parameters of experimental display

对比图7原算法得到的莫尔纹可见度预测表和图6观察人员给出的实验结果，可以看出两者给出的莫尔纹可见度较低的区域（颜色为绿色的区域）在整体位置上有较大的重叠部分，这说明原算法对子像素为非矩形的情况有一定的适用性。但原算法给出的预测结果中在右下角部分存在较大的莫尔纹可见度较低的绿色区域，这与实验结果不相符合，说明原算法存在较大的误差。对比图8新算法给出的莫尔纹可见度预测表和图6观察人员给出的实验结果可以发现，两者给出的莫尔纹可见度较低的区域重叠的部分更大，而且新算法给出的预测结果右下角不再为莫尔纹可见度较低的绿色，而是可见度较高的橙色或者黄色，这充分说明了新算法针对子像素为非矩形的情况具有更高的准确度和可靠性。图7和图8中颜色异常突出的点我们称之为奇异点，奇异点的产生是由测量误差、形状误差和算法本身存在一定误差三者综合作用的结果。奇异点的数量相对较少（图7中322个点只有6个奇异点，占比只有1.86%；图8中奇异点占比只有1.55%），不影响根据预测结果得到所需的金属网格设计参数。

图6 实物匹配结果Fig.6 Practical matching results

图7 原算法特征频率的计算结果Fig.7 Calculation results of the earlier algorithm

图8 新算法特征频率的计算结果Fig.8 Calculation results of the new algorithm

为了量化两种算法和实物匹配结果的吻合度并比较两种算法的性能，需要计算两种算法和实物匹配结果的匹配率。反映吻合度的匹配率有整体匹配率和可用匹配率。整体匹配率是指仿真分类结果与实物匹配结果一致的数量占整体仿真参数总数的比例，可用匹配率是指仿真分类结果中可用的部分与实物匹配结果一致的数量占实物匹配结果中所有可用总数的比例，其计算公式为：

式中A为实物匹配结果中被判定为莫尔纹轻微（即匹配结果中“OK”）的点的数量，B为算法给出的莫尔纹可见度预测表中同时满足大于判断频率且在实物匹配结果中的对应位置也为“OK”的点的数量。

可用匹配率反映了预测结果给出的可用点的可信度大小，其值越接近于1，可信度越高。在实际生产匹配显示屏的触控屏时，多数情况没有显示器实物，无法得到如图6所示的实物匹配结果，这时要找到可用的金属网格参数完全依赖于仿真预测的结果，因此生产商更看重可用匹配率。在判断频率为2 lp·mm-1时，两种算法的整体匹配率和可用匹配率如表2所示。从表2可以看出，新算法的整体匹配率从76.4%提高到79.5%，可用匹配率也从67.57%提高到84.51%，两种评价仿真吻合度的指标均得到了提高，尤其是可用匹配率提高幅度较大，这说明新算法相比于原算法的仿真准确度更高，可靠性更强，能够更好地指导生产。同时新算法相比于原算法在复杂度上没有提升，运行时间与原算法相近。在实际工程应用时，只要求根据预测结果找到相邻的4个点取均值作为设计金属网格的设计参数，考虑到测量误差和观察员的主观误差，可用匹配率超过80%就可以保证能够找到可用的金属网格设计参数。

表2 两种算法的对比Tab.2 Comparison of two algorithms

5 结 论

在利用子像素透过率计算来仿真和分析金属网格触控屏上出现的莫尔纹的算法中，非矩形的子像素被近似当作矩形处理，这种近似在预测子像素形状与矩形差异较大的金属网格触控屏上出现的莫尔纹可见度时误差较大。本文针对其中一种非矩形子像素触控屏，利用计算机模拟生成与原子像素形状更加接近的图形来提高算法的匹配率。在利用二维傅里叶变换得到仿真图片的空间频谱并进行滤波后，得到了特征频率来反映莫尔纹的可见度，通过比较特征频率和判断频率对莫尔纹的可见度进行分类。实验结果表明，以2 lp·mm-1作为判断频率，新算法的整体匹配率从76.4%提高到79.5%，可用匹配率从67.57%提高到84.51%，改进后算法的准确度和可靠性得到了明显的提高，尤其是对指导实际生产更有意义的可用匹配率得到了显著的提高，这对金属网格触控屏的生产厂家利用算法来寻找匹配的金属网格触控屏有重要意义。