多波束与侧扫声呐图像的迭代自适应配准方法

章 宁，金绍华，边 刚，肖付民

海军大连舰艇学院军事海洋与测绘系，辽宁 大连 116018

多波束测深系统(MBES)通过精确测量声波往返的时间和到达角度，可以得到高精度的海底位置和深度信息，同时获得海底声强图像。然而，受成像原理的限制，多波束声图的分辨率较低，图像质量较差，难以反映海底地貌的纹理信息。侧扫声呐系统(SSS)通过接收海底反向散射的时序回波信号，可以绘制高分辨率、高质量的海底回波图像。但是，为了提高探测的分辨率并减弱船体噪声的影响，侧扫声呐通常采用拖曳式安装，导致侧扫图像位置信息不准确。基于此，将多波束和侧扫声呐图像配准融合，可获取位置信息准确且纹理信息丰富的声呐图像，有助于提高海底地形地貌及障碍物的探测精度及海底底质分类能力[1]。

对于多波束与侧扫声呐图像的配准，由于其成像原理的差异性以及海洋环境的复杂性，其配准方法较为复杂[2]。国内外专家学者大多采用基于特征的图像配准方法[3]。文献[4]利用SURF算法实现了多波束与侧扫声呐图像区域的配准和融合。文献[5]利用改进的SURF算法实现高分辨率侧扫图像与低分辨率多波束图像的自动配准。文献[6]通过人为选择特征点对，建立多项式模型来配准多波束和侧扫声呐图像。文献[7]提出了一种基于等深线和轮廓线的同名特征点配准方法，但此方法需要具有测深功能的新型侧扫声呐。文献[8]采用chamfer算法实现多波束侧扫图像自动配准。文献[9]利用成对目标的阴影进行侧扫声呐图像的配准。虽然这些方法很大程度上实现了多波束和侧扫声呐图像的配准，但存在特征点对要求高、图像变换形式简单，以及未顾及图像细节差异等问题。为了顾及声呐图像的细节信息，文献[10]利用改进的非刚性变换算法(Demons算法)对声呐图像进行配准，该配准方法属于基于物理模型的配准方法，能够实现图像的自适应配准。但该算法未考虑多波束图像与侧扫图像之间的分辨率差异，若直接利用Demons算法将侧扫声呐图像配准到多波束图像上，会损失侧扫图像的细节信息，降低融合声呐图像的质量。

为了减弱多波束和侧扫声呐图像分辨率差异对配准融合的影响，同时尽可能保留侧扫声呐图像的细节信息，本文尝试综合利用小波变换、仿射变换和Demons算法实现多波束和侧扫声呐图像的配准和融合。

1 本文方法

1.1 Demons非刚性配准算法

文献[11]首次提出Demons非刚性配准算法。它最早来自光流(optical flow)算法，光流是用来估计视频影像中相邻的两帧图像目标间的微小位移量。Demons算法根据图像间对应像素点的灰度梯度计算出位移向量v，通过每一次移动向量v，使待配准图像逐像素地配准到参考图像。该算法的前提假设是图像灰度在变换过程中保持不变即

I(x(t),y(t),t)=c

(1)

式中，I表示图像灰度；t表示图像变换经历的时间；x(t)、y(t)表示t时间内图像横、纵方向上的变化；c表示一个常量。对式(1)求微分得

(2)

假设两图变换时间t为单位时间，则有

(3)

式中，s表示参考图像灰度信息；m表示待配准图像灰度信息，将其代入式(2)可得

v·∇s=m-s

(4)

式中，v=(∂x/t,∂y/t)；∇s表示参考图像灰度的梯度向量。进一步变换可得到经典Demons算法的基本方程

(5)

(6)

式(6)得到的位移量v能够准确描述图像间灰度的变化情况。为了提高Demons算法的收敛速率及配准精度，文献[12]提出了Active Demons算法，该算法结合牛顿第三定律，将原始算法中移动图像的单侧力驱动改成合力驱动，即

(7)

式中，参数α为均化系数，用于调节图像单次位移的幅度，α越大单次位移量越小，收敛速度越慢，每次调节的幅度越细微；反之则算法收敛越快，但配准越粗糙。

为此，在进行图像配准时，一般先采用较大的α值迭代，然后再使用小的α值继续精化迭代，这样设置的配准算法收敛速度快且配准精度高。

在Demons算法中，待配准图像中的每一个像素点都能够随着灰度梯度自由移动，这样会出现图像变换不够平滑的现象。因此需要在每一次迭代中利用高斯滤波器对位移场进行平滑处理，从而得到配准所需的最佳图像变换模型[13]。

1.2 声呐图像的多尺度分解与重构

Demons配准算法可以实现像素级别的图像配准，但是对于多波束和侧扫声呐图像配准而言，侧扫声呐图像具有更加丰富的细节信息，若利用Demons算法将尺度较小的侧扫声呐图像配准到尺度较大的多波束图像上，将会损失侧扫图像的细节信息，为此，本文在图像配准前先对侧扫声呐图像进行多尺度分解，利用分解得到的低频信息重构图像，将大尺度的侧扫声呐图像与多波束图像进行配准。

小波变换由于能够解决时间域与频率域分辨率的矛盾[14]，可以将图像在独立频带和不同空间上分解为低频信息和高频信息，因此广泛应用于图像处理[15]。目前，基于小波变换的多尺度分解算法主要有金字塔状结构算法(PWT)[16]和树状结构算法(TWT)[17]，本文采用经典的PWT算法[18]。如图1所示，每一次变换，可以将图像分解成4个相同尺寸的小波分解图像，分别表示低频部分信息(LL)、水平方向高频信息(HL)、竖直方向高频信息(LH)和对角方向的高频信息(HH)。

图1 小波分解Fig.1 Wavelet decomposition

由此可见，采用PWT算法可将图像分成低频信息和高频信息，前者表示图像的总体轮廓即大尺度信息，后者体现图像的纹理细节即小尺度信息。

进一步，将侧扫声呐图像小波分解后得到的LL部分进行重构，得到与原侧扫图像尺寸相同的大尺度图像，将其与尺度相近的多波束图像实施配准。

1.3 仿射变换

传统的利用Demons算法进行图像配准时，使用的参考图像和待配准图像之间存在的差异较小，因此可以直接利用该算法求得的位移场进行配准[19]。然而在多波束图像和侧扫声呐图像中，由于海洋环境等因素的影响，图像中会存在较多噪声，使得图像的可视性差且灰度变化复杂[20]。如果直接使用Demons算法的结果只会配准到全局图像每个像素点灰度差异较小的位置，而对于整体框架的配准并不准确。为此，本文首先利用仿射变换对二者声呐图像进行粗配准。

仿射变换是一种常用的基于特征的图像变换方法，它利用匹配的特征点对解算配准变换矩阵，该方法能够保证图像中线条的平行关系不变，且所需要的控制点对数较少，但是其配准较为粗糙，且配准效果与特征点的选择密切相关[21]。

1.4 顾及尺度差异的迭代自适应配准方法

基于上述算法模型，综合考虑多波束和侧扫声呐图像特点及配准融合目标，构建了顾及尺度差异的迭代自适应配准方法，方法流程如图2所示。

图2 顾及尺度差异的迭代自适应配准方法Fig.2 Iterative adaptive registration method considering scale difference

(1) 对侧扫声呐图像进行PWT小波分解，将提取的LL层低频信息重构成与原图像大小一致的侧扫声呐低频图像。

(2) 提取多波束图像与原始侧扫声呐图像的匹配特征点对，并利用仿射变换得到粗配准的旋转变换矩阵。

(3) 将侧扫声呐低频图像经过矩阵旋转变换，得到粗配准侧扫声呐低频图像。

(4) 以多波束图像作为参考图像，粗配准侧扫声呐低频图像作为待配准图像，利用Demons配准算法进行迭代自适应配准，累积每一次迭代的位移场作为Demons配准变换模型。

(5) 将原始侧扫声呐图像先后经过矩阵变换模型和Demons配准变换模型，得到最终的融合配准声呐图像。

针对上述步骤，式(7)可进一步改化为

(8)

式中，T表示由仿射变换得到的变换矩阵；T(m)表示经过仿射变换粗配准后的图像。

由此可见，与现有的多波束与侧扫图像配准算法相比，本文提出的迭代自适应配准方法充分考虑到了两者图像尺度的差异，将小波变换算法融入配准算法中，并结合仿射变换与Demons算法进行配准。利用较少的特征点对，就可以实现同时考虑图像整体框架和细节特征的配准，最终得到高质量的多波束与侧扫声呐配准图像。

2 实例验证与分析

为了验证本文配准方法的有效性，特采用实测数据进行分析说明。

2.1 实测图像的选择

实测数据来源于青岛胶州湾海域的同一海底区域，由Klein 4000侧扫系统采集的侧扫声呐数据和R2Sonic 2024浅水多波束系统采集的多波束数据组成。为了减小海底复杂环境的影响，以达到最佳匹配效果，首先将测区进行分块，对每一块区域单独进行配准。在两幅声呐图像中分别选取320×320像素的小区域，对多波束和侧扫声呐图像进行辐射畸变改正、几何畸变改正、图像增强、回波异常值改正和噪声抑制等预处理后[22]，得到改正后的多波束和侧扫声呐图像分别如图3和图4所示。

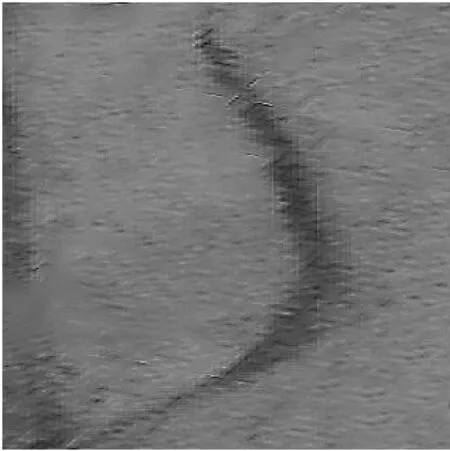
图3 多波束图像Fig.3 MBES image

图4 侧扫声呐图像Fig.4 SSS image

对比图3和图4可以看出，侧扫声呐图像纹理信息特别丰富，多波束图像的位置信息相对准确，两者融合，可实现优势互补。

2.2 图像的配准

按照本文提出的配准方法，首先采用小波变换对侧扫声呐图像进行处理。

声学仪器的水下分辨率受多种因素的影响，不同测量仪器在不同水深的横、纵分辨率都不相同。本文试验所使用的侧扫声呐和多波束数据分别由Klein 4000侧扫系统和R2Sonic 2024浅水多波束系统采集得到，通过仪器的参数说明以及关于声呐图像分辨率的相关文献，可以得到Klein4000侧扫声呐的横向分辨率约为2.0 cm，纵向分辨率约为2.4 cm[23]，R2Sonic 2024在40 m左右水深(本次试验水深约为40 m)的横向分辨率约为40 cm，纵向分辨率约为34 cm[24]。

对于二维小波分解而言，每一次分解得到的低频图像，其横向分辨率与纵向分辨率较变换前的图像均增大一倍。因此，若要将多波束图像与侧扫声呐图像归到同一级别的分辨率，则需将侧扫声呐图像进行4层小波分解后，提取第4层图像的低频信息，并用其重构得到低频图像，这样得到的低频侧扫声呐图像与多波束图像在同一尺度，其结果如图5所示。

图5 侧扫声呐低频图像Fig.5 Low frequency image of SSS

其次，根据海底特征物的特点，通过人工选取特征点对的方式，在两幅原始的声呐图像中选取阴影的上下边界点和阴影横向最宽点构成4对匹配特征点对，如图6所示。

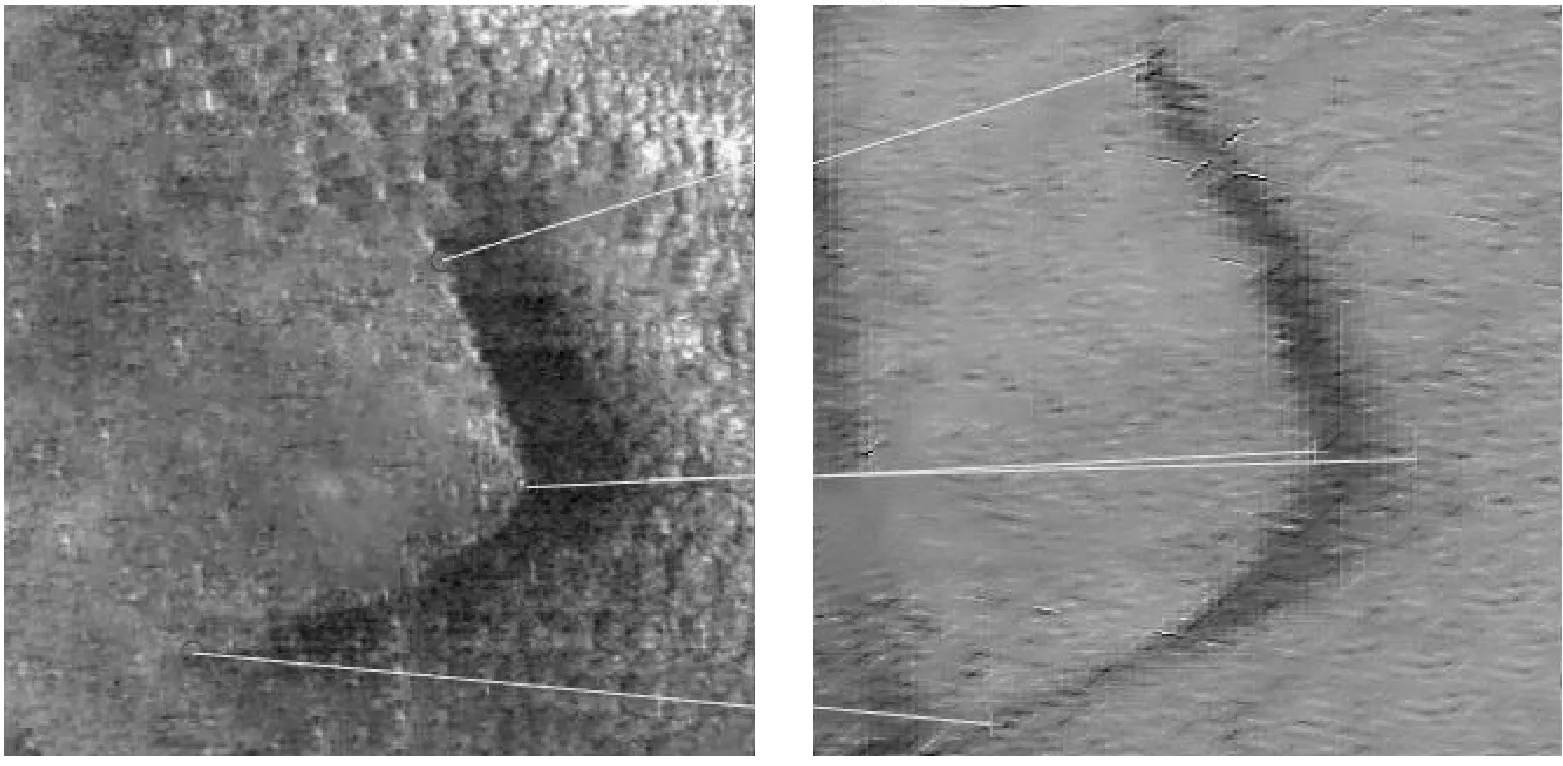
图6 特征点对匹配Fig.6 Matching of feature point pairs

利用图6选择的配准点对结合仿射变换对图3和图5两幅声呐图像进行粗配准，得到变换矩阵为

(9)

进一步，对侧扫声呐的低频图像进行仿射变换，得到图7所示的变换结果。

由图7可以看出，经过仿射变换粗配准后，侧扫声呐图像的整体框架已经基本与多波束图像匹配，但一些细微的地方匹配并不完善。进一步利用Active Demons算法对粗配准图像进行自适应迭代精配准。利用模板尺寸60×60、标准差为10的高斯低通滤波器进行平滑处理，设置迭代次数150次，其中α=1.0的120次，α=1.5的30次，最终得到的低频精配准图像如图8所示。Active Demons算法的变换模型如图9所示，左侧表示未经变换的标准格网，右侧表示迭代150次后所有位移场的叠加。

图7 仿射变换后的侧扫低频图像Fig.7 Low frequency SSS image after affine trans-formation

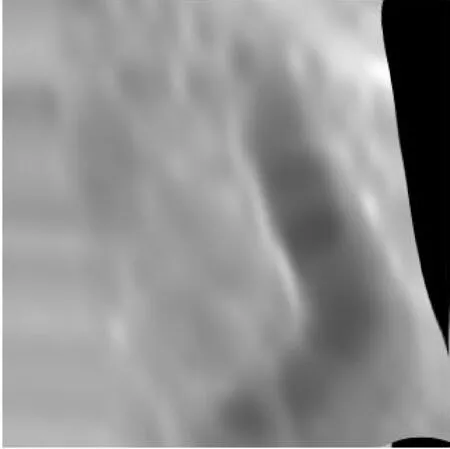
图8 经Demons算法配准后的侧扫低频图Fig.8 Low frequency SSS images after registration by Demons algorithm

图9 Active Demons算法变换模型Fig.9 Active Demons algorithm transformation model

2.3 配准评价指标

为了定量评价配准效果，采用均方差(mean square error,MSE)和互信息值(mutual information,MI)作为评价指标[25-26]

(10)

式中，n和m分别表示横纵方向上图像的像素点个数；s(i,j)与m(i,j)表示两图中每个像素点对应的灰度值。MSE值越小，表示图像之间差异越小，配准效果越好

MI(s,m)=H(s)+H(m)-H(s,m)

(11)

式中，H(s)、H(m)、H(s,m)分别表示参考图像的信息熵、待配准图像的信息熵及两图之间的联合信息熵。对于2维图像，信息熵的计算方式如下

(12)

(13)

式中，i表示图像中的灰度值；hi表示图像中灰度i对应的像素点个数；N表示图像的灰度级数；pi表示灰度i出现的概率。联合信息熵则需要利用两幅图像的联合直方图，基本方式与计算信息熵类似。MI值越大，表示两图像相关性越大，配准效果越好。

在每一次迭代之后，分别计算得到MI和MSE，如图10和图11所示。

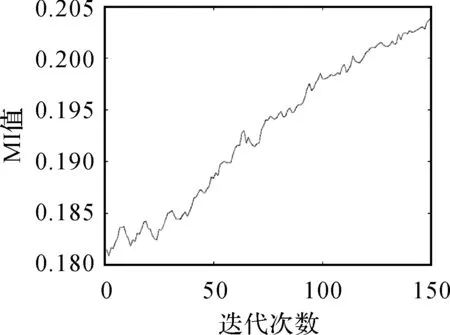
图10 MI变化曲线Fig.10 MI change curve

图11 MSE变化曲线Fig.11 MSE change curve

由图10和图11可以看出，随着迭代次数的增加，MI值不断增大，表示多波束和侧扫图像相关性增强；MSE值不断减小，说明两图像之间的差异变小，以上均表明，随着迭代次数的增加，配准效果越来越好，这也充分证明了迭代自适应配准方法的有效性。

最后，将之前的仿射变换模型及保存的Demons配准变换模型先后用于原始的侧扫声呐图像上，最终得到侧扫声呐图像的配准结果如图12所示。

图12 最终配准结果图像Fig.12 Final registration result image

比较图12和图3可以看出，配准后的图像既获得了多波束声呐图像准确的位置信息，还保留了侧扫图像丰富的纹理信息。

为了进一步说明本文方法的有效性，本文分别计算了原始侧扫声呐图像与多波束图像在配准前、仿射变换粗配准后、Demons算法精配准后3个阶段的MI和MSE值(表1)。

表1 配准算法各阶段的MI和MSETab.1 MI and MSE of each stage of the registration algorithm

由表1可以看出，较配准前，经仿射变换粗配准后MI提高了41.6%，MSE降低了25.6%，经Demons算法精配准后MI提高了45.2%，MSE降低了28.2%。

为进一步说明本文配准方法的有效性与可行性，在同一测区不同条带选择另外一处特征地物进行重复试验，其多波束图像与侧扫声呐图像分别如图13和图14所示。

图13 试验2多波束图像Fig.13 MBES image in the second experiment

图14 试验2侧扫声呐图像Fig.14 SSS image in the second experiment

重复上述试验步骤，利用本文提出的顾及多波束与侧扫声呐图像尺度差异的迭代自适应配准方法对以上两幅图像进行配准，最终得到的配准结果如图15所示。

图15 试验2最终配准结果Fig.15 Final registration result image in the second experiment

为进一步说明本文配准方法与其他基于特征的配准算法相比效果更佳，将两次试验的多波束与侧扫声呐图像采用文献[1]使用的多项式配准模型进行配准，同样利用MI和MSE两个指标对配准效果进行衡量，最终得到的对比试验结果见表2。

表2 对比试验结果Tab.2 Result of contrast experiment

由表2可以看出，在两次试验中，相比于仿射变换与多项式配准方法，利用本文配准方法得到的图像MI值最大且MSE值最小，这表明其最终得到的配准结果效果最佳，配准质量最好，进一步验证了本文方法的有效性。

由此可见，与直接使用基于特征的配准方法相比，本文提出的顾及多波束与侧扫声呐图像尺度差异的迭代自适应配准方法可以有效提高二者图像配准质量，最终得到既有准确的位置信息又有丰富纹理信息的声呐图像。

3 结束语

多波束和侧扫声呐图像配准融合是获取高质量声呐图像的有效途径。本文提出的迭代自适应配准方法，充分顾及了多波束与侧扫声呐图像的特点，引入小波变换算法提取侧扫图像的低频信息，并进行大尺度侧扫图像重构；提出利用仿射变换对声呐图像进行粗配准，减少配准的框架差异；利用Demons算法对重构的低频侧扫图像和多波束图像进行迭代自适应配准，并给出了详细的操作流程及评价指标。通过两次实例数据验证分析表明：本文方法在保留侧扫声呐图像纹理细节的基础上实现位置配准。对比两次试验配准前的评价指标，经仿真仿射变换后MI分别提高了41.6%和93.1%，MSE分别降低了25.6%和18.4%，经多项式模型配准后MI分别提高了37.7%和95.4%，MSE分别降低了25.6%和19.1%，经本文的配准方法后MI分别提高了45.2%和96.7%，MSE分别降低了28.2%和19.9%，进一步验证了本文方法的有效性与准确性。

本文研究成果实现了多波束与侧扫声呐图像的配准与融合，获得位置准确且纹理丰富的声呐图像，有望提高海底地貌探测、障碍物探测和海底底质分类的精度及可靠性。