基于区间二型模糊控制器的主蒸汽温度串级控制系统仿真

倪仲俊

（浙江浙能乐清发电有限责任公司, 浙江温州 325609）

火电厂主蒸汽温度是火电厂安全、高效运行的重要参数, 由于其具有大惯性、大迟延特性, 主蒸汽温度的控制一直是研究热点。而PID控制器实现简单, 参数易于整定, 被广泛应用于火电厂控制系统中。对于主蒸汽温度控制系统, 较为常见的控制策略为串级控制, 其外回路为PI控制器, 内回路为P控制器[1］。实际运行效果表明, 虽然PID串级控制策略在主蒸汽的温度控制中具有一定的效果, 但尚不能满足当前节能、增效的要求。

模糊PID控制器作为一种非线性控制器, 在某些应用场合, 其控制效果要优于PID控制器[2-4］, 文献[5-9］将模糊PID控制器应用于火电厂主蒸汽温度的控制。虽然模糊PID控制器具有较好的控制效果, 但由于其隶属度函数是确定的值, 在处理系统不确定方面（比如被控对象模型变化、系统扰动等）的能力不强。Mendel等[10-11］提出了一种区间二型模糊逻辑系统, 其核心概念是基于Zadeh提出的二型模糊集合[12］。与传统一型模糊集合不同, 二型模糊集合的隶属度由首隶属度和次隶属度构成, 在处理系统不确定性方面具有很大优势。二型模糊逻辑系统与传统一型模糊逻辑系统的最大区别就是存在降阶操作, 首先将二型模糊集合降阶为一型模糊集合, 然后得到最终的解模糊化结果。因此, 区间二型模糊控制器在实现上比一型模糊控制器更加复杂。文献[13］提出了一种简单的区间二型模糊PID控制器设计算法, 利用偏差作为模糊控制器的输入, 模糊推理的规则数大大减少。该控制器采用常用的区间二型模糊降阶算法——KM降阶算法[14］。KM降阶算法通过迭代计算得到2个端点, 取平均值作为最终的解模糊化结果。

本文利用一种直接降阶算法——NT降阶算法, 将区间二型模糊控制器应用于串级控制系统的外回路控制器。该降阶算法不需要迭代即能得到最终的解模糊化结果[15］。仿真结果表明, 与传统PID控制器以及基于KM降阶算法的区间二型模糊控制器相比, 本文提出的控制器能够降低系统超调, 加快系统的稳定时间。当系统存在减温水扰动时, 能够迅速消除扰动, 达到稳态值。

1 区间二型模糊集合

针对论域X, 设其中的元素为x, 则二型模糊集合可定义为

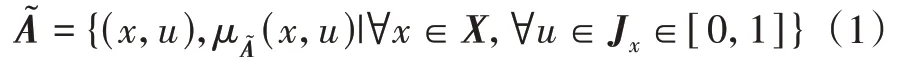
其中,u为首隶属度函数,μA͂(x,u)为次隶属度函数。

如果二型模糊集合的次隶属度函数定义为1, 则被称为区间二型模糊集合, 即

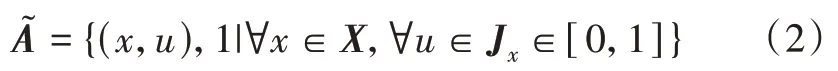
以三角隶属度函数为例, 其示意图如图1所示。

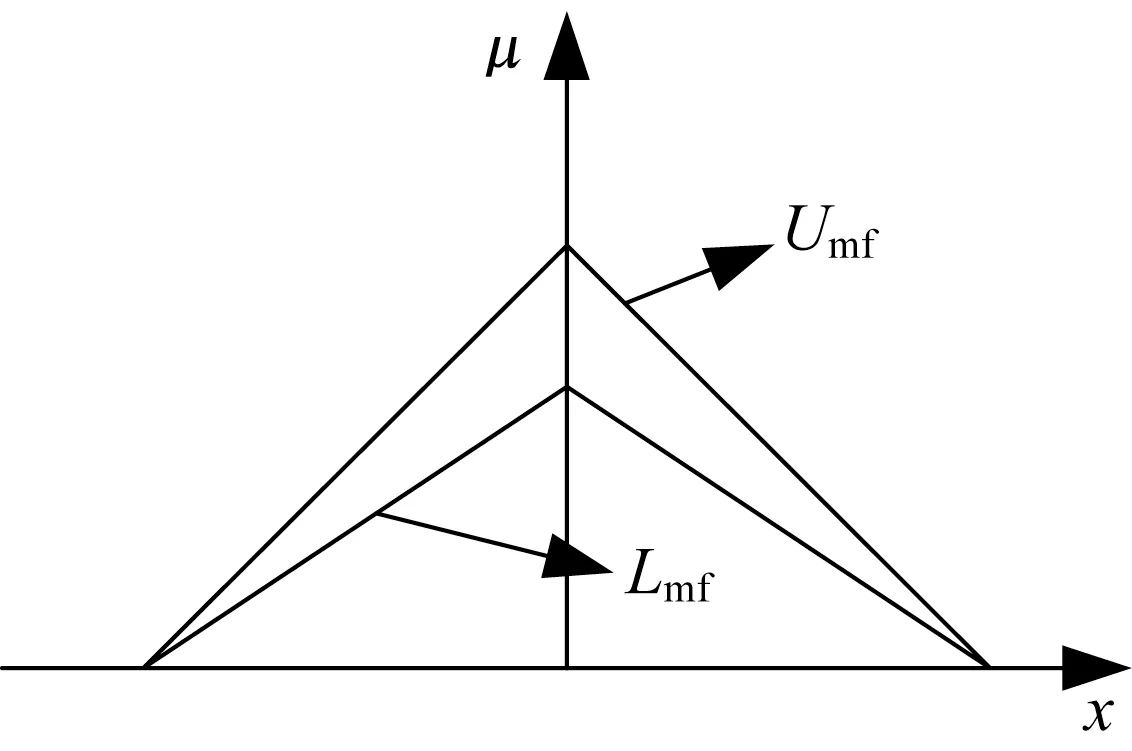
图1 首隶属度函数Fig.1 Primary membership function

图1中的Lmf为首隶属度函数的低限,Umf为首隶属度函数的高限, 二者组成了区间二型模糊集合的不确定域（Footprint of Uncertainty, FOU）。

2 主蒸汽温度串级控制系统

主蒸汽温度对象可分为导前区和惰性区, 一般采用喷水减温方法来控制主蒸汽温度。如果采用单回路来控制主蒸汽温度, 控制效果并不是很理想。在实际中一般引入能够提前反应的导前信号, 构成多回路控制系统。目前采用较多的是串级控制系统, 典型的主蒸汽温度串级控制系统方框图如图2所示[1］。

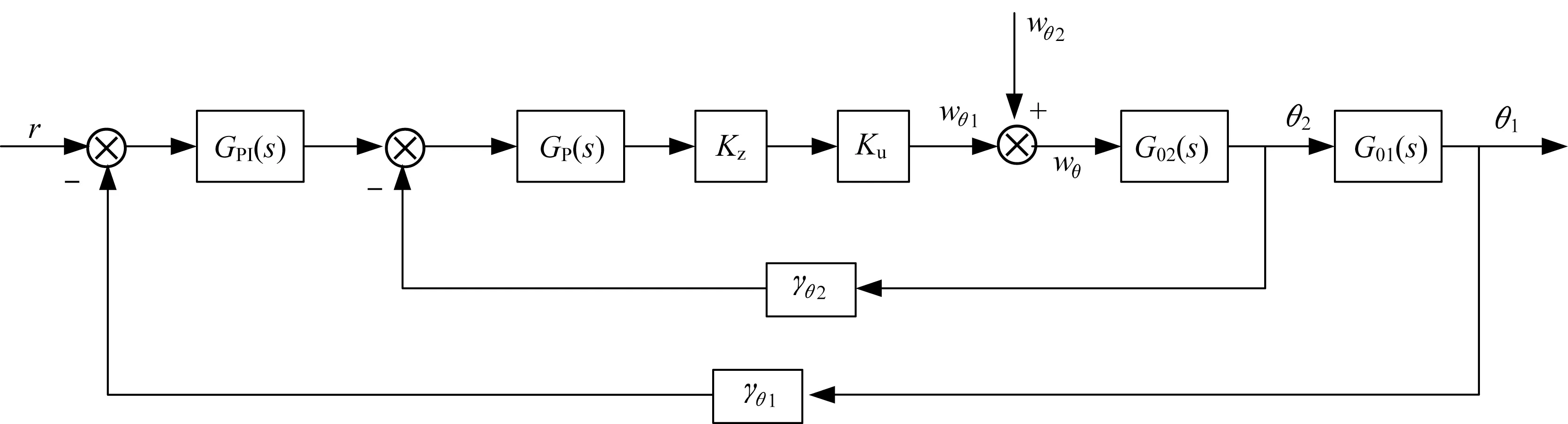
图2 主蒸汽温度串级控制系统方框图Fig.2 Block diagram of the main steam temperature cascade control system

图2中,Kz为执行机构的传递系数,Ku为喷水调节汽门传递系数,γθ1和γθ2为温度传感器系数。wθ1为调节作用下减温水量,wθ2为扰动作用下减温水量,wθ为总减温水量。G02（s）为导前区对象传递函数,G01（s）为惰性区对象传递函数。文献[1］对系统进行了简化,Kz=Ku=1,γθ1=0.1以及γθ2=1, 且定义了主蒸汽温度对象的传递函数为

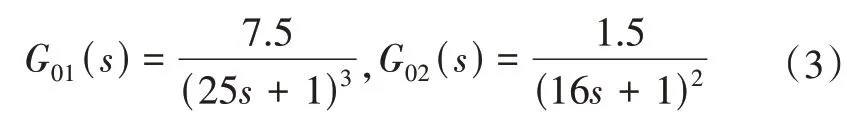
控制器形式为

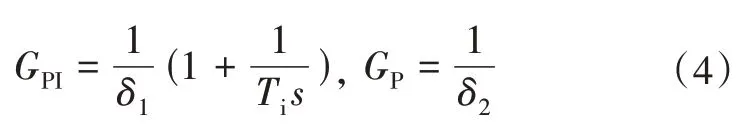
内、外回路的控制器参数可通过先内后外的工程整定法来确定, 最终使得系统的阶跃响应曲线衰减率ψ=0.75时的控制器参数为δ1=4.0964,Ti=13.13,δ2=0.365。

3 本文算法

一种简单的区间二型模糊控制PID器如图3所示[13］。

由图3可以看出, 该模糊控制器只有1个输入, 即系统偏差e（t）。利用量化因子Ks将e（t）转换到模糊系统的输入论域中, 经过区间二型模糊推理系统得到模糊系统的输出efuz（t）, 通过PID控制器参数KP,KD,KI得到控制器的输出u（t）。

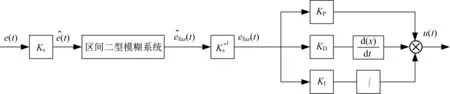
图3 区间二型模糊PID控制器Fig.3 Interval type-2 fuzzy PID controller

本文区间二型模糊控制器输入e（t）经过量化因子Ks, 将模糊系统的论域定义为[-1, 1］。采用三角隶属度函数, 二型模糊集合的不确定域通过参数m1和m0来实现, 如图4所示。

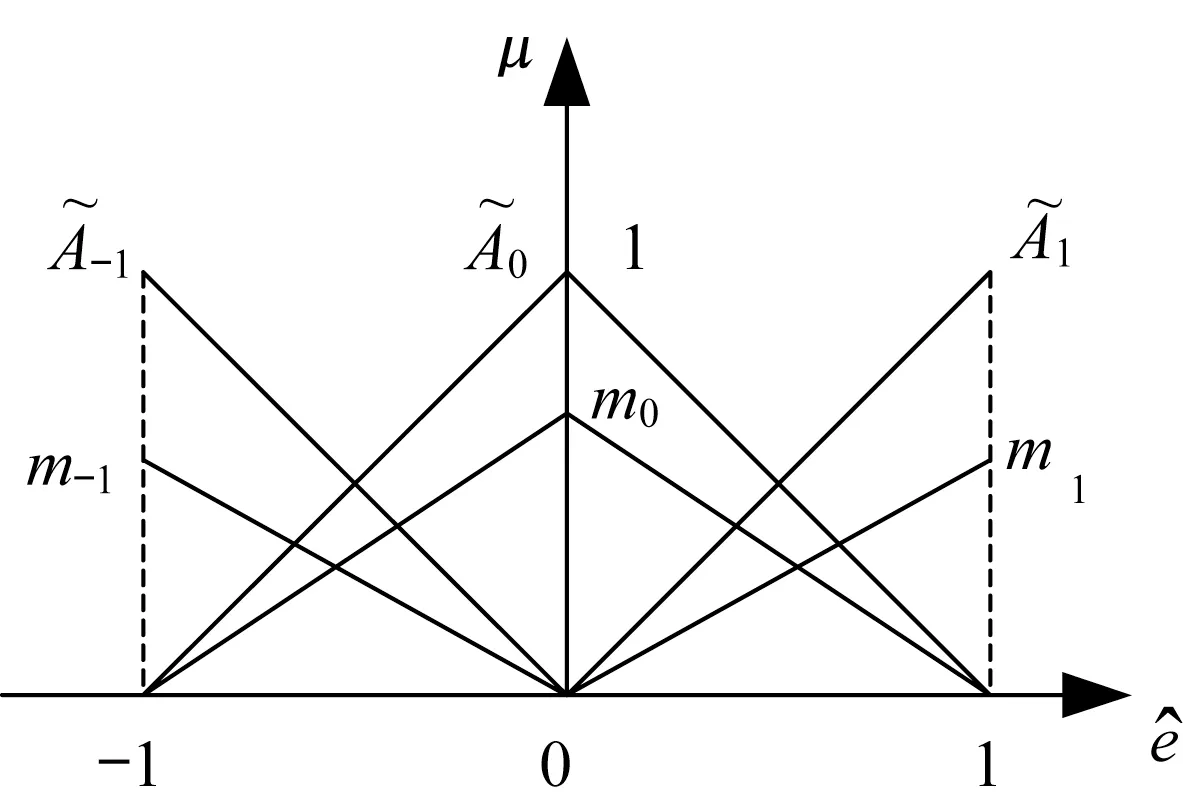
图4 本文首隶属度函数Fig.4 Primary membership function of the proposed

图4定义了3个模糊集合, 则模糊控制具有3条模糊规则, 对应的后件参数yi, 描述如下：

与文献[13］不同, 本文利用NT直接降阶算法[15］, 不需要进行迭代操作即得到解模糊化结果。设任意采样时刻t, 激发的模糊规则的隶属度高、低限为, 则解模糊化结果为

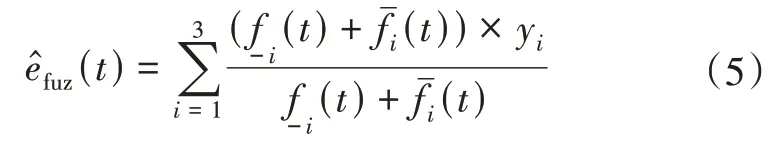
最终本文提出的区间二型模糊控制器的输出u（t）为

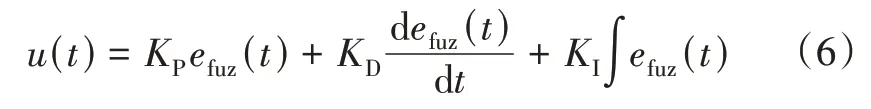
4 仿真研究

本文仿真实例中串级控制系统的外回路控制设为区间二型模糊PID控制器, 内回路依然为P控制器。根据第2节的说明, 外回路控制器参数为Kp=1/δ1=0.2441,KD=0,KI=1/（δ1×Ti）=0.0186, 内回路控制器参数为Kp=1/δ2=2.7397。区间二型模糊控制器除了上述参数之外, 还包含2个参数m1=0.2以及m0=0.9, 后件参数定义为y1=-1,y2=0以及y3=1。由于θ1温度传感器的反馈系数γθ1=0.1, 当设定值为单位阶跃输入时, 最终的稳态值应该为10。

4.1 单位阶跃输入

图5显示了单位阶跃输入下, 系统输出曲线和主控制器输出曲线。

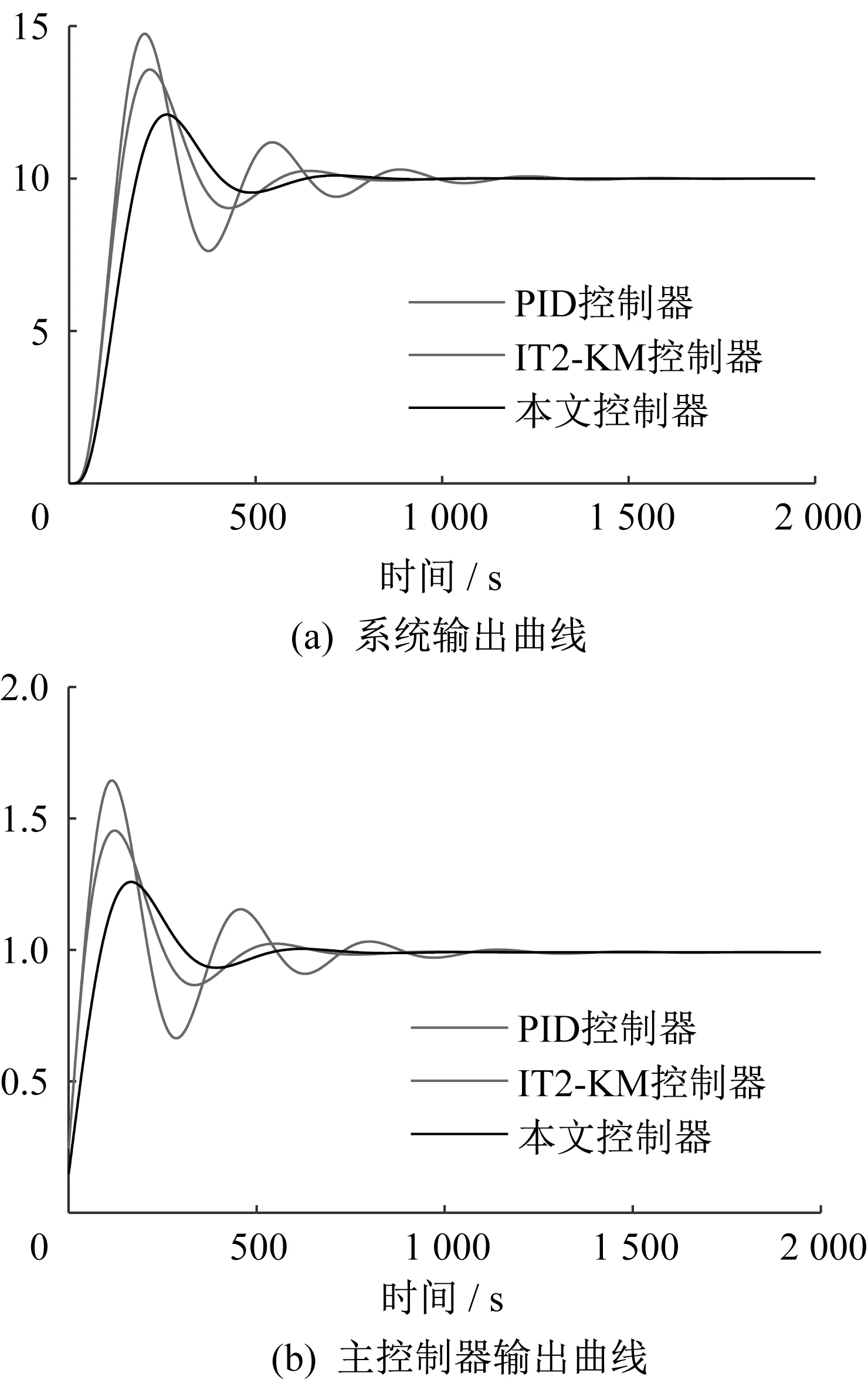
图5 单位阶跃下系统响应曲线Fig.5 System response curve under unit step

表1列出了3种控制系统的主要性能指标, 其中稳态时间设定为系统输出达到设定值的±2%, IAE为误差积分准则, 则

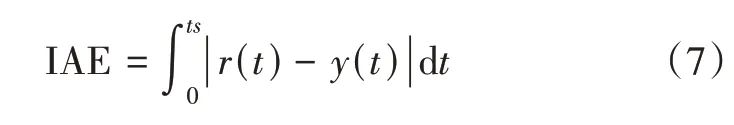
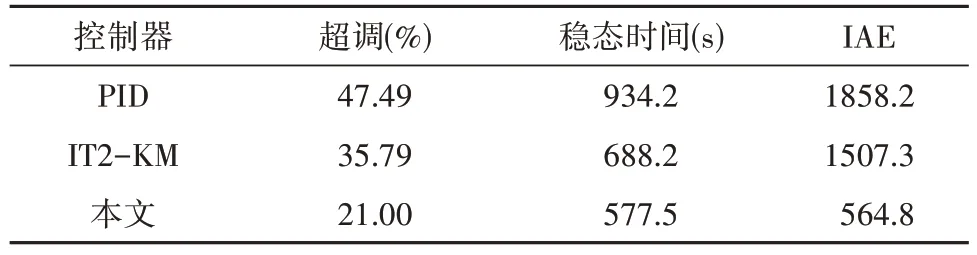
表1 3种控制系统主要性能指标Tab.1 Main performance indexes of 3 control systems

4.2 减温水扰动

图6显示了减温水扰动下, 系统输出曲线和主控制器输出曲线。

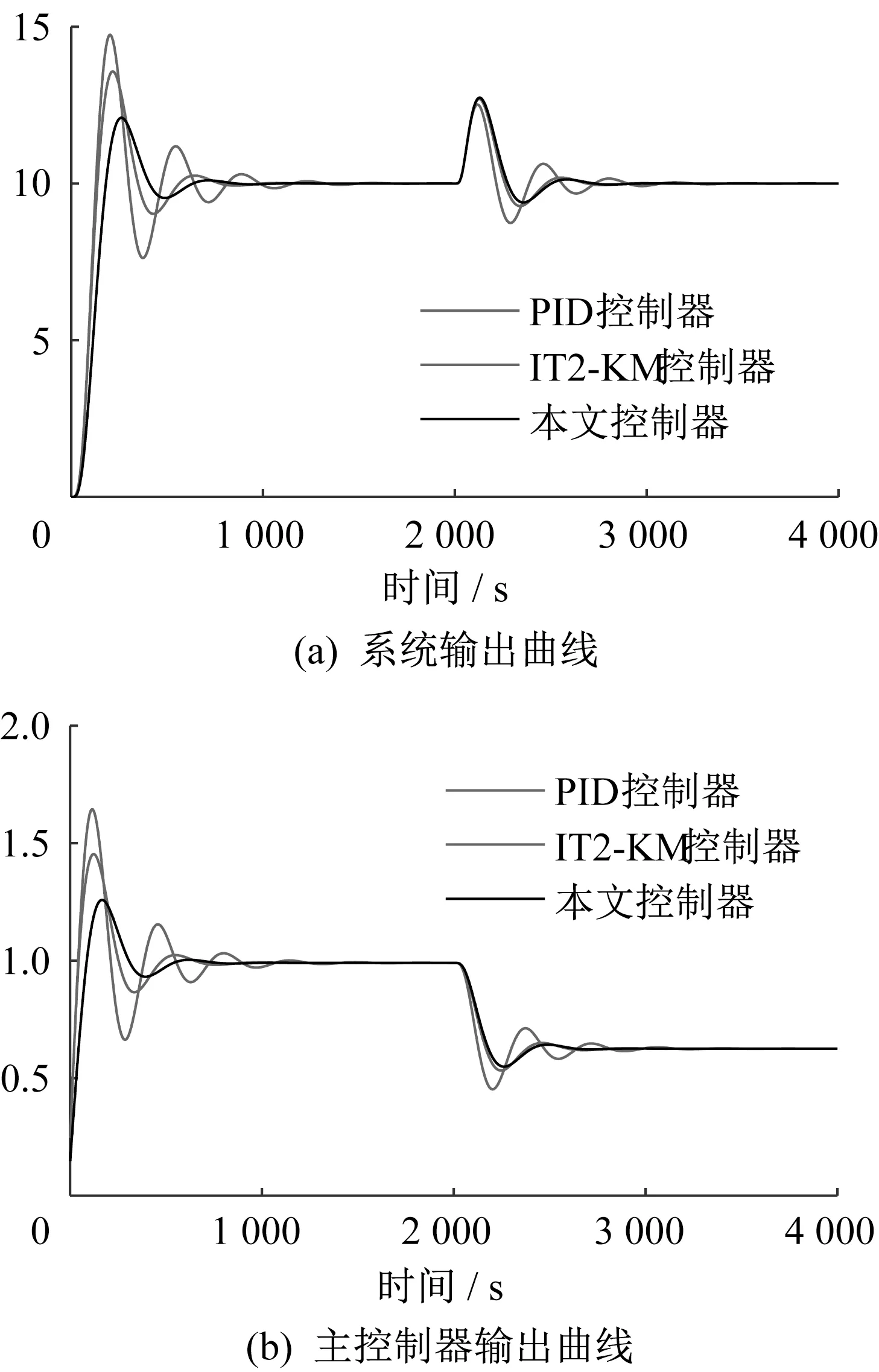
图6 内部扰动下系统响应曲线Fig.6 System response curve under internal disturbance

5 结 论

本文提出了一种区间二型模糊PID控制器, 该控制器采用系统偏差作为模糊系统的输入, 利用直接降阶算法, 避免了常用KM降阶算法迭代计算过程。通过对主蒸汽温度串级控制系统的仿真, 结果表明与PID控制器、基于KM降阶的区间二型模糊PID控制相比, 本文提出的控制系统能够减小系统超调, 加快系统达到稳态的时间。而且当系统存在内扰, 也即减温水扰动时, 能够快速消除扰动, 使系统能够快速达到稳态。