一种新的电力系统脆弱性评估方法

赵毓鹏, 苗 晗, 刘 祯, 耿滋钧, 张一丹

（1.国网思极网安科技（北京）有限公司, 北京 102211；2.北京中电飞华通信有限公司, 北京 100070）

为了将大型互联复杂电力系统的稳定性保持在安全极限范围内, 许多学者提出了不同稳定指数计算电力系统各母线脆弱性, 并设计了许多优化算法模型[1-3］。文献[4］提出了攻击者-防御者（AD）模型, 以评估暴露于自然灾害的电力系统的脆弱性, 并利用自适应稳健框架开发了三级优化模型, 以提高自然灾害下相互依存的电力系统基础设施的恢复力。但是该算法模型存在随机性太强、计算时间长等缺点。文献[5］使用三层优化模型和嵌套列约束生成（Nested Column and Constraint Generation, NC-CG）算法来评估综合电力燃气系统的脆弱性, 还采用了元启发式算法来解决AD问题, 但在实验中发现脆弱性评估值与实际值相差较大, 可能与元启发式算法的本身缺陷有关。

1 拟议的电网综合脆弱性指数

本文提出了一种新的综合指标, 用于电力系统及其相关部件的脆弱性分析, 使用公理化设计概念来开发电力网络的新型CVI算法模型, 分为以下步骤。

步骤1：为了采用公理化设计概念来描述任何电网结构, 有必要在现有流程和资产之间建立关联, 提供这种关系的二进制矩阵称为关系矩阵RM。本研究定义了2个二元关系矩阵：转换关系矩阵RMC和传输关系矩阵RMT。这两个矩阵的每个元素都称为电网事件, 显示流程和资产的可行组合。为了评估和量化电网的能力, 应通过顺序矩阵RMn将转换和传输关系矩阵组合在一起。同样的概念通常适用于电力系统约束CMU[6］。

为了有效计算电力系统负载约束能力, 本研究应用了阻抗-负载电路模型, 其电路架构示意图如图1所示。

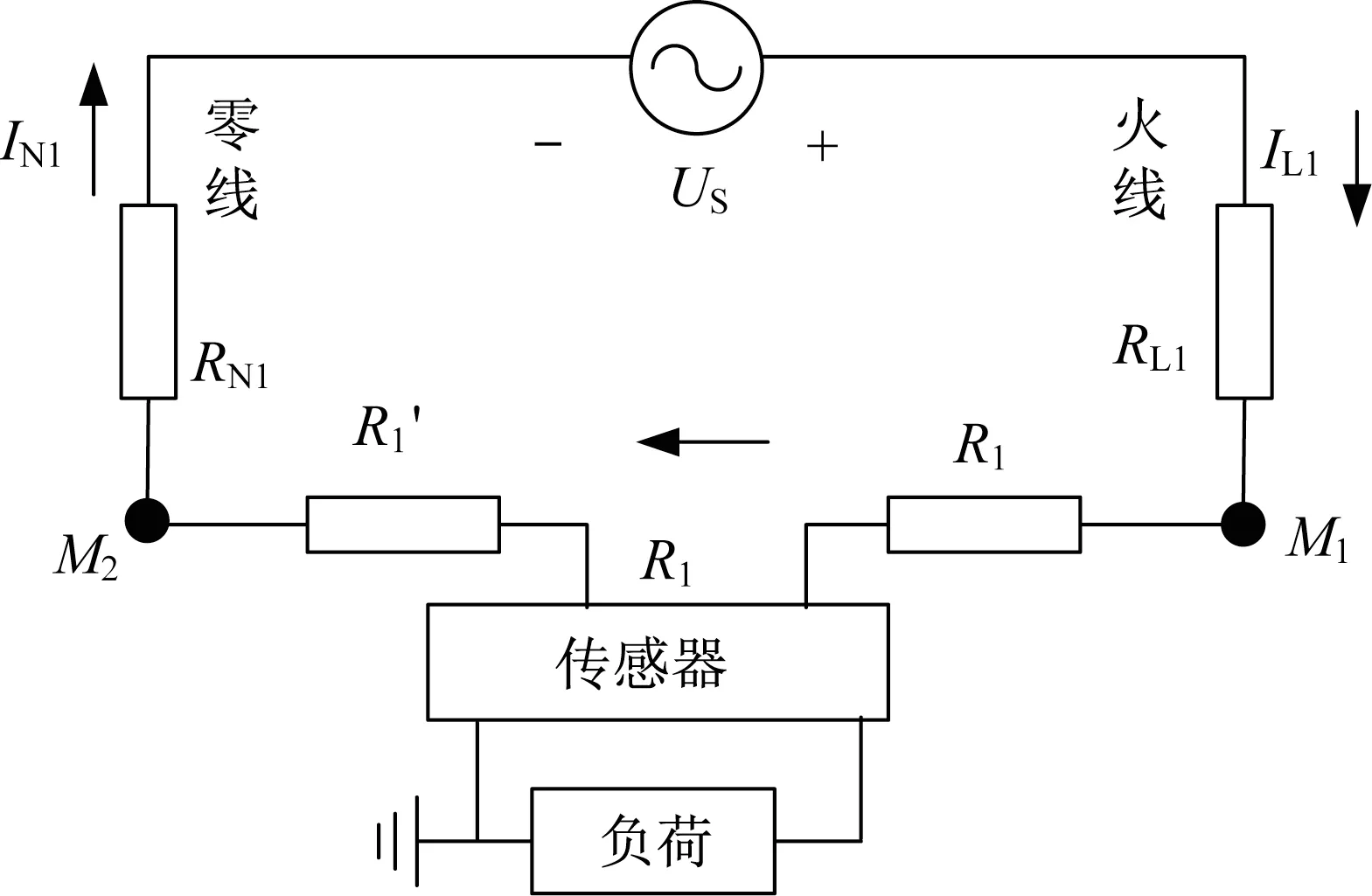
图1 阻抗-负载电路图Fig.1 Impedance-load circuit diagram

如图1所示, 为了便于数据采集, 在配电网用户端设立了传感器, 使传感器在电网电路中形成阻抗-负载电路模型。该回路包含了火线、零线、配电变压器、传感器支路和若干个接入支路的端点M。在正常情况下该回路阻抗不会发生突变, 回路阻抗也可以反映负载的情况变化。其中高压流经台区的配电变压器变压用字母Us表示其低压信号, 在配电变压器两端处, 分别连接火线（L）和零线（N）, 其中火线上的电流总量为IL, 零线上的电流总量为IN。其中R1为火线经端点M流入支路的电流所经过的等值阻抗,IL1为流过火线上阻抗所剩的电流值[7-8］。R1′为经过传感器到零线端点M的电流所经过的等值阻抗,IN1为流过零线上阻抗所剩的电流值。电力系统中线路的负载计算如下：

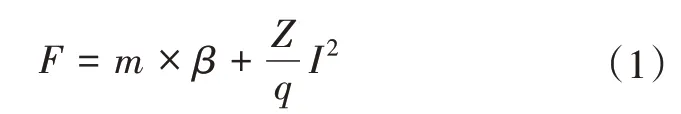
式（1）中,F表示线路总负载过载量,m表示电容器实际容量,β表示电容器的介质因数,Z表示电抗器基波频率下的电抗,q表示电抗器在基波频率下的品质因数, 通过式（1）对电力系统中线路的负载进行计算。

步骤2：评估电力系统脆弱性需要提供一组DOS, 每个DOS由一组服务事件（service events, SE）组成。当所有SE都被执行时, 这些SEs将向第i个耗电元件供电。例如, 如果一个电力系统有m个发电厂和n个承载量, 则DOS的总数为m×n。实际上, 每个SE都是一个指定的转换过程, 可以作为DOS的一部分应用[9］, 即

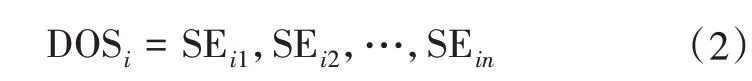
式（2）中, SE是一组服务事件。DOSP是在SE对SE的基础上指定DOS的可能性。为此, 有必要定义一个新的矩阵, 以指示一系列SE是否可以实现DOS（可能性）或无法实现。对于每个DOS, 可能性可在2个二进制矩阵中捕获。

（1）DOS转换可能性矩阵（CPM）定义：对于给定的DOSj, 如果SE实现转换过程（Processes Conversion, Pc）, 应创建大小为n（SEj）×n（PC）的二进制矩阵CPMi, 其常取值等于1。

（2）DOS传输可能性矩阵（TPM）定义：对于给定的DOSj, 如果SE实现传输过程（Process Transmission, PT）, 应创建大小为1×n（PT）的二进制矩阵TPMi, 其常取值等于1。

步骤3：CVI算法模型将基于每个DOS可能路径的完整枚举, 为此, 电网系统必须通过转换事件在发电厂产生, 然后通过一个或多个连续传输事件传输。最后, 为了向负载输送功率, 连续传输事件通过转换事件结束到负载[10］。为了量化CVI评估参数, 有必要根据3种类型的顺序服务事件矩阵定义路径枚举, 将这些矩阵相乘, 可以确定DOS 的总路径数SM, 即

式（3）中,i与j为服务事件常序数,m和n（DOSi）分别是每个电力系统负载中可能路径和DOS的数量, 可以根据任何中断前后可能路径的数量定义线路脆弱性评估指标。SMCT是传输事件紧跟转换事件矩阵, SMTT是2个连续的传输事件矩阵, SMTC是转换事件再传输事件矩阵。随后, 脆弱性指数VI在式（3）中以规范化方式给出, 即

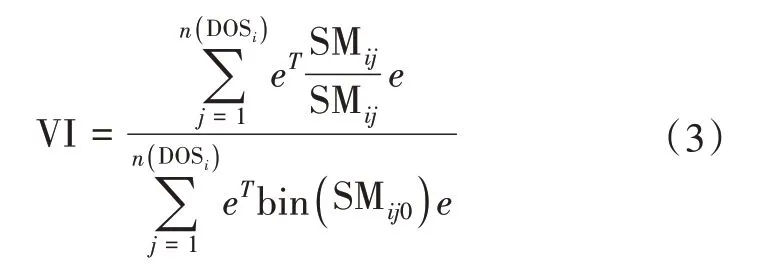
式（3）中, bin（）是一个二进制函数, 所有正值返回1, 否则返回0。e是一个列向量, 其条目均为1, 下标0表示正常操作。

步骤4：需要考虑一些重要的电网特性, 例如发电机容量、负载预先指定的优先级以及由于输电线路（拥塞）的容量限制而将电力输送到负载的一些限制。为了解决这些限制, 采用本文所提出的综合脆弱性指数（CVI）, 即

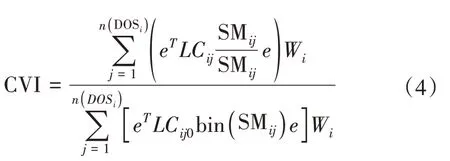
式（4）中,LCij是向第i个电力系统负载提供服务序数j的功率,Wi是电力系统负载加权系数, 此指标参数值介于0（最小脆弱性）和1（最大脆弱性）之间。

2 基于简单电网网络的评估模型

本文采用直流（DC）最优潮流参数对网络进行建模, 最大的CVI显示了最脆弱的电力系统服务事件。电网由一个燃气轮机发电厂组成, 具有压缩、燃烧和发电3个过程, 需要注意的是, 应考虑发电机和负载的引线, 便于将负载或发电机节点与母线节点分开。其中, 转换（RMC）和传输（RMT）关系矩阵如图2所示。

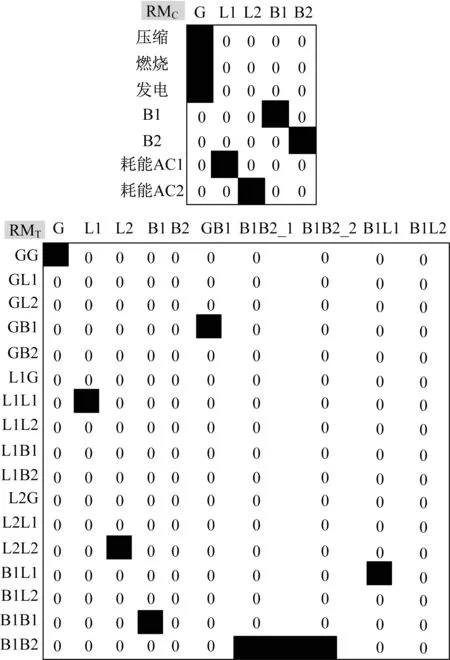
图2 简化电网模型的转换和传输关系矩阵Fig.2 Transformation and transmission relationship matrix of simplified grid model

RMC中记录了每个转换过程对每个资产的适用性, RMT中记录了每个传输过程对每个资产的适用性, 将转换和传输关系矩阵组合在一起则为顺序矩阵RMn, 该矩阵存在2个DOS：一个是发电机和负载#1之间的路径, 另一个是发电机和负载#2之间的路径[13］。因此, 这些DOS的转换可能性矩阵（CPM）如图3所示。

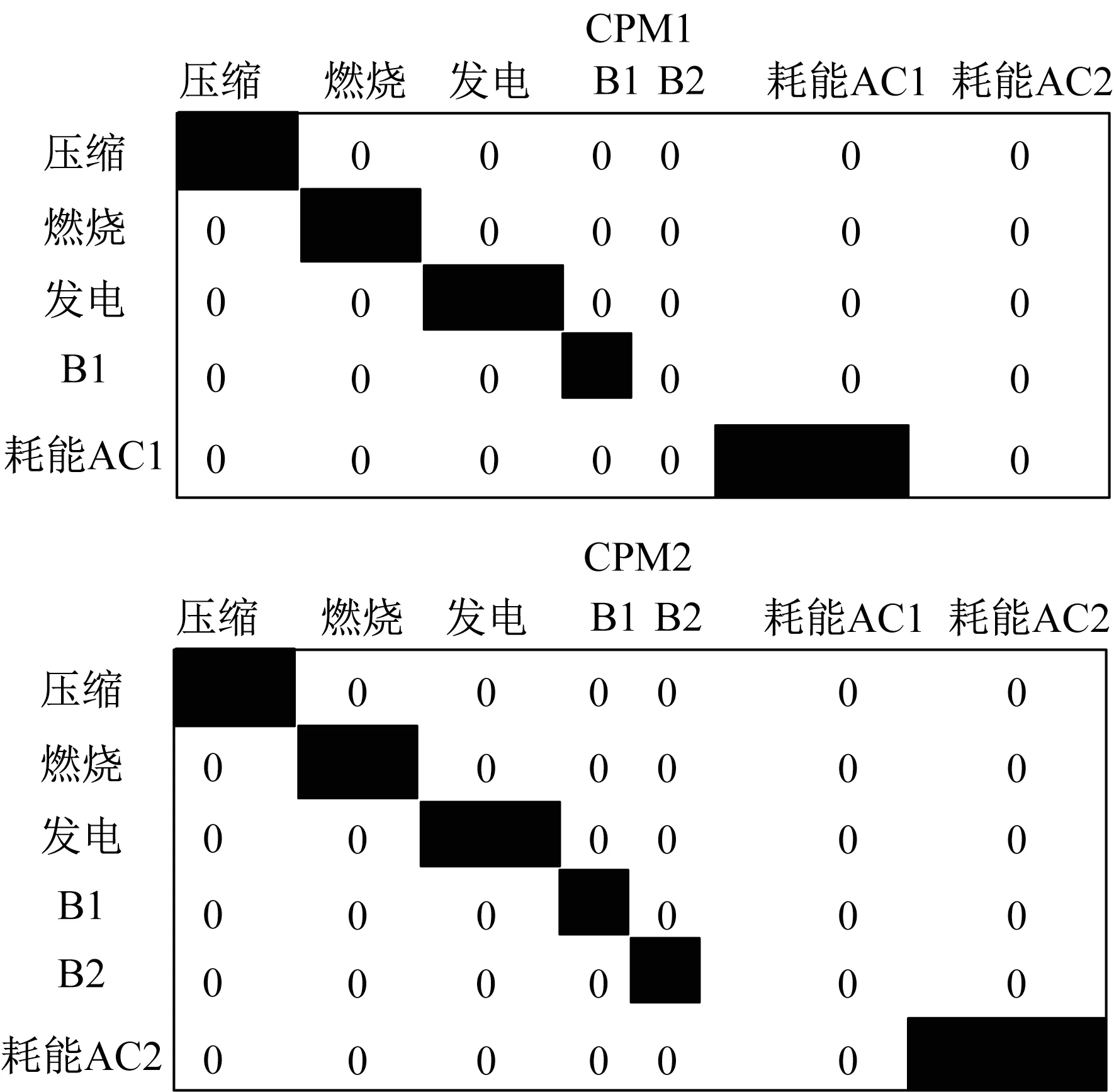
图3 简化电网模型的转换可能性矩阵Fig.3 Transformation possibility matrix of simplified power grid model

为了衡量简单电网在不同条件下的脆弱性, 考虑了5种类型的中断：发电机停止运行、B1-2线#1和B1-2线#2的故障以及负载线#1和负载线#2的停止运行。为了显示负载在CVI计算中的重要性, 假设2组负载加权系数（第一种情况, 当负载#1为临界负载时,W1=0.7和W2=0.3；第二种情况, 当负载#2为临界负载时,W1=0.3和W2=0.7）。根据式（1）～（4）, 列出第一种情况下的中断结果与拟定CVI的相应值（表1）、第二种情况下的中断结果和拟定CVI的相应值（表2）, 2种情况下每次负载线中断的电力系统脆弱性评估参数CVI仿真曲线分别由图4和图5显示。

根据以上结果得出以下结论：

（1）从表1和表2可以看出, 在其中一条B1-2线路发生中断时, 输电阻塞会影响负载2和CVI的供电。例如, 如果B1-2线#1发生故障, 由于B1-2线#2的容量限制, 只能提供50 MW。另一方面, 在B1-2线#2中断的情况下, 由于B1-2线#1有足够的容量, 可以提供负载#2的全部功率。因此, 在这种情况下, 电网的脆弱性比前一个更大。研究表明, 当负载#2为临界负载时, 模拟电网的CVI低于负载#1为临界负载时的CVI。这是因为B1-2线#2的容量限制和负载#2（100 MW）的更大消耗。

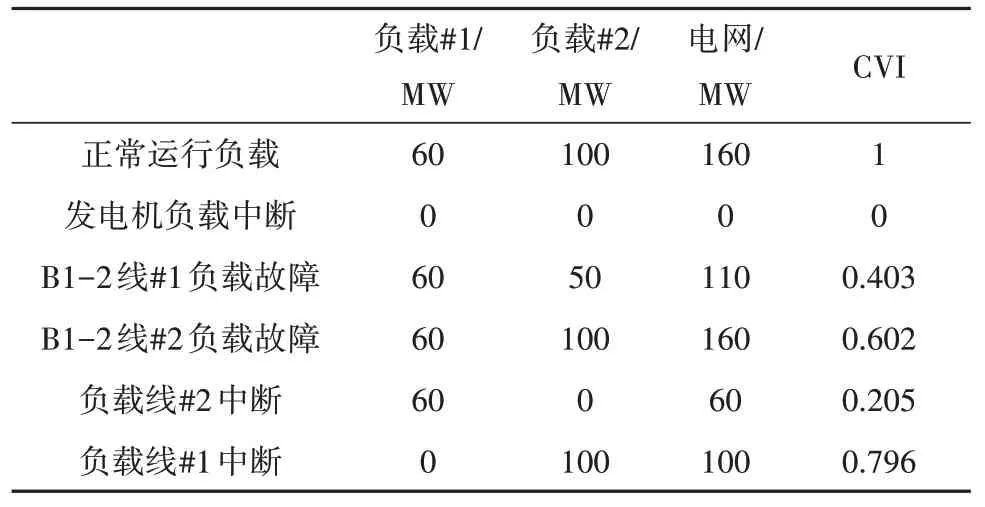
表2 情况二向负载供电参数Tab.2 Load power supply parameters in Case 2

（2）图4和图5显示, 无论负载的重要性程度如何, 由于B1-2线#2的拥堵, B1-2线#1比B1-2线#2更重要。脆弱性指数的最小值出现在发电厂部件中断和线路（及其连接的母线）中断的情况下, 而最大值出现在负载线路#1故障的情况下。

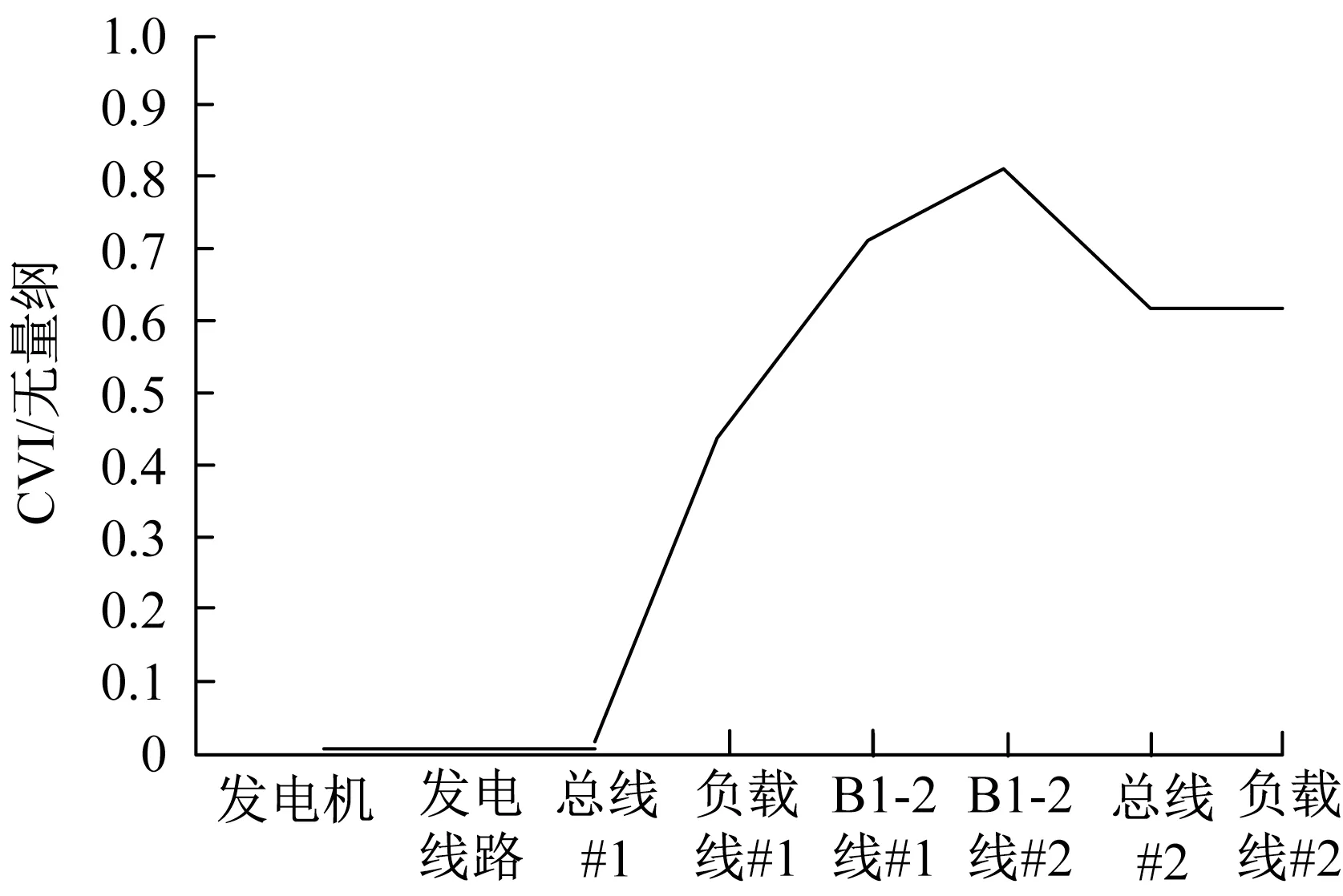
图4 情况一负载线中断的CVI仿真图Fig.4 CVI simulation diagram of load line interruption in Case 1

图5 情况二负载线中断的CVI仿真图Fig.5 CVI simulation diagram of load line interruption in Case 2

（3）对于发电机部件的中断和与发电机相连的线路或母线的中断, 脆弱性指数CVI为0（表1）。在模拟电网模型中, 当负载#1为临界负载时, 与负载线#2停止运行相比, 负载线#1停止运行导致脆弱性指数进一步降低, 反之亦然。

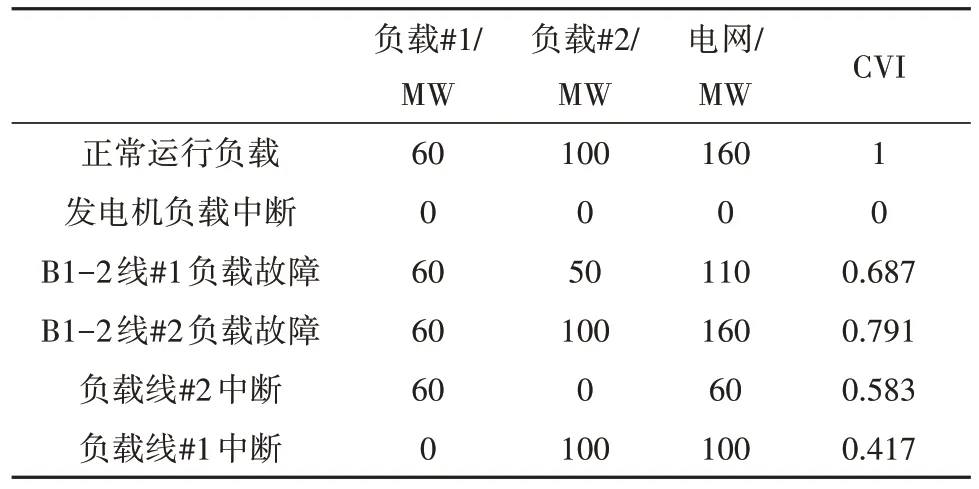
表1 情况一向负载供电参数Tab.1 Load power supply parameters in Case 1

3 实验与分析

实验中计算机的硬件配置CPU为Inter Core i7-9700H, 运行内存为3200MHz 8×6GB, 硬盘大小为5TB。此外, 仿真与电网建模软件采用电力系统分析综合软件包（Power System Analysis Systhesis Package, PSASP）, 关于IEEE-14总线测试系统架构如图6所示。

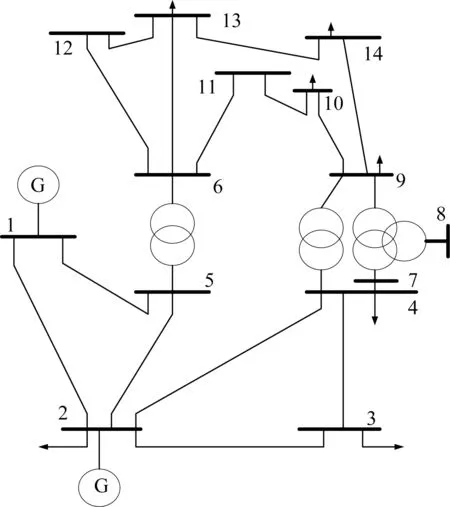
图6 IEEE-14总线测试系统架构Fig.6 Architecture of IEEE-14 bus test system

如图6所示, 本研究使用所提出的方法评估14总线系统的脆弱性, 以识别关键节点（母线）。当假设所有负载权重系数相同时, 总线#10和#11的排名大致相同。让负载#7为临界负载, 这种情况下5-6#线的停止运行将最大限度地降低拟建CVI, 而该线是最脆弱的。5-6#线连接高压和中压的电力系统, 因此, 其故障对系统脆弱性的影响最大。

本研究将以文献[5］所提出的NC-CG方法与本文方法应用于IEEE-14总线测试系统各线路的脆弱性评估情况, 通过PSASP软件计算得出不同方法的节点脆弱性指标结果如表3、4所示。

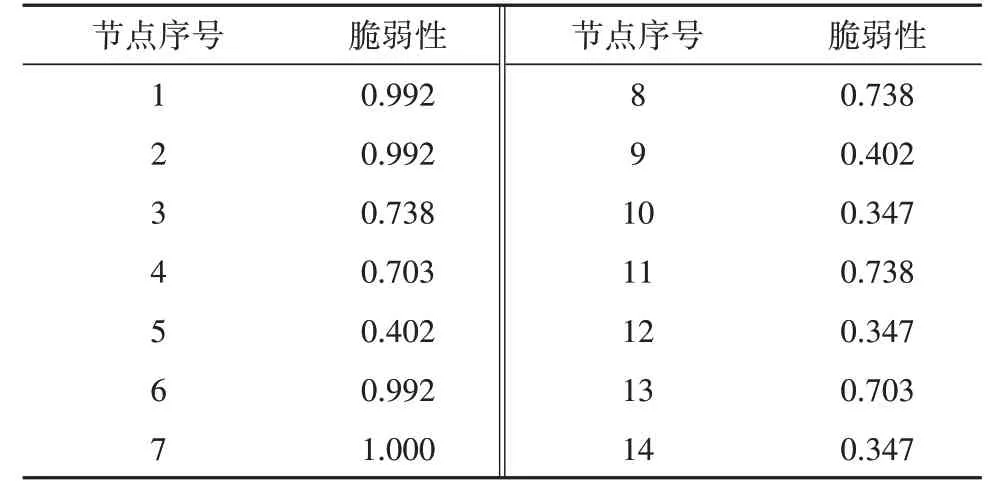
表3 NC-CG方法脆弱性评估情况Tab.3 Vulnerability assessment of NC-CG method

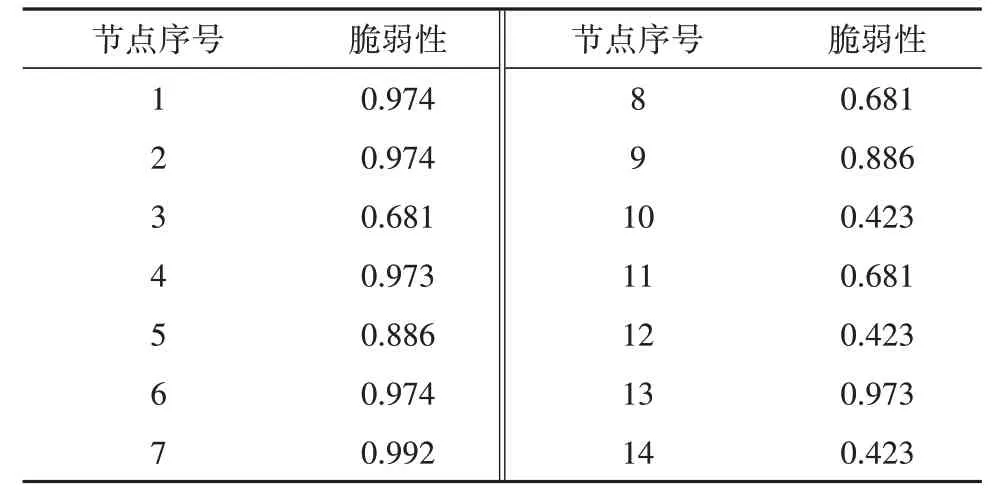
表4 本文方法脆弱性评估情况Tab.4 Vulnerability assessment of the proposed method

从表3、4不难看出, 某些总线节点脆弱性相同, 例如总线#1与总线#2与总线#6、总线#3与总线#8与总线#11等, 为了便于实验对比将这些脆弱性相同的总线联立在一起, 与实际脆弱性进行作差取其误差值, 并将其结果融合在一起, 得到各线路脆弱性评估性能对比如图7所示。

图7 各线路脆弱性评估性能对比Fig.7 Comparison of vulnerability assessment performance of each line

从图7中可以看出, 本研究所提出的CVI虽然在总线#1-2-6与7中误差高于文献[5］所提出的NC-CG评估指标, 但整体上CVI平均误差较低, 均小于6%, 而文献[5］方法在评估总线#4-13与5-9中误差较高, 其中后者误差值超过了10%, 由此可见, 本研究开发的电力系统脆弱性评估指标CVI更加具有可行性, 可广泛应用于城市大型电网公司。

4 结 语

为了评估和量化电力系统的脆弱性, 提出了一种基于矩阵的综合脆弱性指数CVI, 该方法基于公理化设计概念和资产和流程的可用组合, 在考虑负载优先级的情况下, 量化中断前后的可行路径来定义。该方法能够定量分析系统脆弱性, 可应用于分布式能源集成的电力系统规划, 由于基于该方法的二进制矩阵, 所提出的评估指标对于优化问题非常有效, 如果负载更大且更为关键, 则CVI会因该负载的线路停止运行而进一步降低。