机器人运动轨迹神经网络模糊控制优化*
2022-09-27崔海花
崔海花
(河南科技职业大学机电工程学院,周口 466000)
0 引言
近年来,随着劳动成本的增加,在许多制造业中,机器人正在逐步替代人类去执行相应的工作任务。特别是人类在探索太空,海洋、核环境等[1-2]危险环境中,通过远程操控机器人可以完成复杂的工作任务。但是,我国机器人技术研究起步太晚,与发达国家先进机器人相比,还存在一定的差距。国外对机器人先进技术也采取了保密和垄断措施,这也导致了机器人研发面临各种困难。机器人在运动过程中,需要各个关节相互配合完成某一特定任务,除了要克服自身重力外,还要保持负载的平衡。若控制系统设计不当,就会造成机器人发生振动现象,失去稳定,导致机器人末端运动轨迹产生较大的误差问题,轻者损坏加工产品,重者造成严重的财产损失。基于上述原因,必须加快机器人技术自主研发技术,打破国外机器人先进技术的垄断,促进国际社会的共同发展。
当前,为了提高机器人控制系统输出精度,国内、外专家学者研究出了机器人多种控制系统。KRISHNA、段焜等[3-4]研究了机器人模糊自适应PID控制系统,分析了机器人控制理论,定义了模糊规则,设计了机器人模糊PID控制器,给出了机器人仿真模型图,可以用来防止机器人产生超调量。XIU、葛媛媛等[5-6]研究了机器人模糊滑模控制系统,创建了机器人运动轨迹示意图,推导机器人不确定非线性数学模型,对传统滑模控制器进行改进,设计出机器人的模糊滑模控制系统,通过实验分析机器人跟踪精度,降低了机器人抖动幅度。SEVIL、尹奇辉等[7-8]研究了机器人模糊神经网络PID控制系统,推导了机器人一阶运动学方程,定义了机器人运动误差方程式,设计了模糊神经网络控制器,利用神经网络逼近算法调整控制参数,通过仿真对机器人输出误差进行测试,控制效果较好。过去研究的机器人大多在空载条件下进行仿真,但是,在负载条件下运动时,容易受到负载因素干扰,导致机器人输出误差较大。对此,本文建立三关节机器人平面简图,给出机器人动力学方程,为了提高机器人在负载环境中抑制外界干扰,采用遗传算法优化神经网络模糊控制器,采用MATLAB软件对机器人关节运动进行仿真,对比优化前和优化后机器人运动位移跟踪精度,比较负载条件下,误差跟踪效果,为改进机器人控制精度,提供一种优化方法。
1 机器人运动轨迹
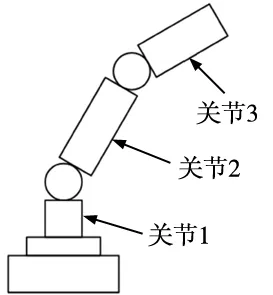
图1 机器人
为了控制机器人位置,必须知道操纵器的动力学特性,以确定驱动它所必须施加的力的大小:力不足意味着操纵器反应太慢。过大的力会使机器人与外部物体碰撞或在所需位置附近振荡。由于系统具有大量的自由度和非线性,因此,推导机器人的运动动力学方程并非易事。机器人的动力学模型包括产生扭矩的动态执行器控制机器人和链的动力学,将动力传输到给出的执行器连杆。将采用第1、第2和第3个运动关节对机器人进行建模,如图1所示。
机器人动力学方程式[9-10]定义为:
M(q)q′′+H(q,q′)+G(q)+F(q,q′)=τ
(1)
式中,M(q)为2×2惯性矩阵;H(q,q′)为2×1科里奥利/离心矢量;G(q)为2×1重力矢量;F(q,q′)为2×1摩擦力矩;q、q′、q′′为2×1位置、速度和加速度向量;τ为2×1广义关节力矩矢量。
机器人动力学要求施加可实现的轨迹。位置、速度和加速度的连续性使机器人能够通过控制装置继续沿着轨迹运行。可以通过方程给出的三阶多项式轨迹来保证这种连续性:
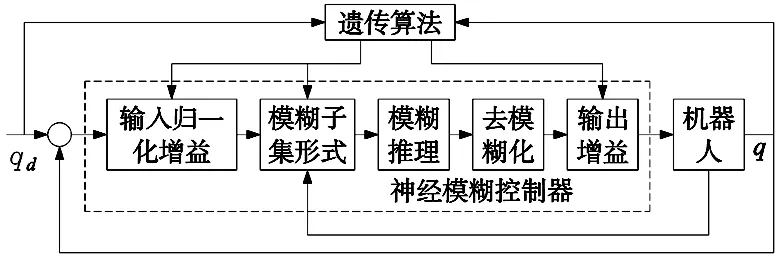
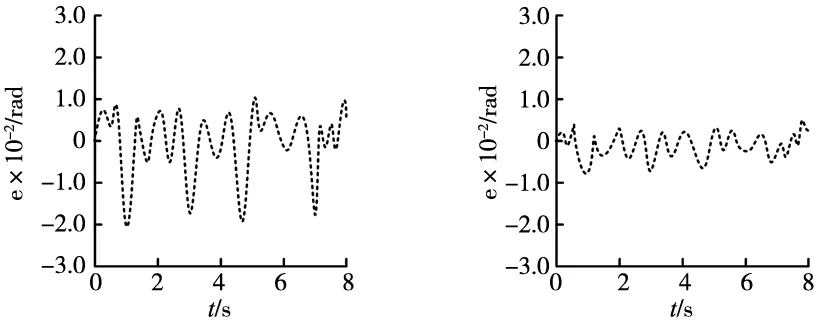
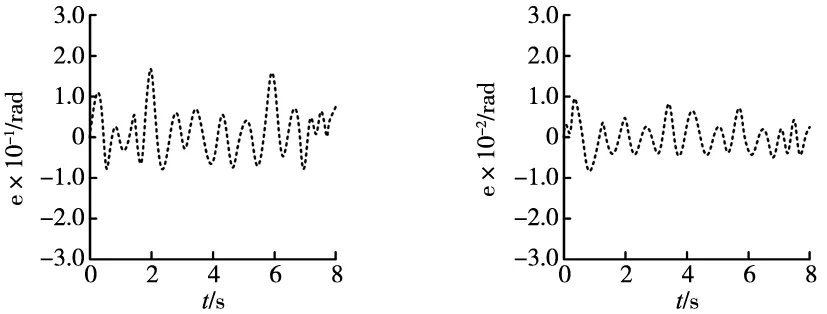
qd(t)=a0+a1(t-t0)+a2(t-t0)2+ (2) (3) 遗传算法是一种基于遗传学和自然选择原理的优化和搜索技术[11]。遗传算法允许由多个个体组成的群体在指定的选择规则下进化到最大化“适应度”(即最小化成本函数)的状态。 遗传算法中的每一个循环都会产生一个给定问题的新一代可能的解决方案。在第一阶段,创建一个初始种群,以启动搜索过程。种群的元素被编码为染色体的位串。字符串的性能,通常称为适应度,然后在表示问题约束的一些函数的帮助下进行评估。根据染色体的适应度,选择它们进行后续的遗传操作过程。选择过程主要负责确保最适合的个体存活。当种群串的选择结束时,将执行由两个步骤组成的遗传操作过程。在第一步中,执行交叉操作,将每两个选定字符串(染色体)的位(基因)重组。任意两条染色体的交叉点是随机选择的。遗传操作过程中的第二步称为突变,染色体上一个或多个随机选择的位置上的位发生改变。突变过程有助于克服局部最大值的陷阱。遗传操作过程产生的后代是下一个要评估的群体。 模糊控制器的一般结构由模糊化块、推理机和反模糊化块组成。此外,模糊控制器必须包含基本知识。其中一个模糊逻辑问题是缺乏从采集的数据中提取模糊规则的系统工具。这个问题有时很难解决。因此,为了避免专家问题,研究人员尝试用几种方法代替专家,如神经网络。 人工神经网络(ANN)是一组形式化的神经元,它们在层(或子组)中关联且并行运行。在网络中,每个小组独立于其他小组进行运行,并将其分析结果传输给下一个小组。提供给网络的信息将逐层传播,从输入层传播到输出层,不经过一个或多个过渡层(称为隐藏层)。应当注意的是,根据训练算法,还可以具有向后传播的信息(“反向传播”)。通常(除了输入层和输出层),一层中的每个神经元都连接到前一层和下一层的所有神经元。采用自适应神经模糊推理系统方法,通过在线学习每个关节来调整控制器参数,以获得良好的控制性能。自适应网络形式的调节器结构如图2所示。它包含第2个和第3个关节的连续误差ei和误差变化Δei作为输入,以及每个关节的驱动关节τi作为输出。神经网络控制算法[12-13]如下: (1)第1层,该层中每个节点的输出为: (4) (5) (2)第2层,该层的节点输出表示为: (6) (3)第3层,节点输出如下所示: (7) (4)第4层,该层的节点具有可调参数,其功能如下: (8) (5)该层仅包含一个节点,该节点执行前一层节点输出的总和为: (9) (10) 图2 神经网络调节器结构 扩展卡尔曼滤波器能有效地估计非线性动力系统的状态。参数估计的应用之一是对神经网络参数进行估计。因此,采用扩展卡尔曼滤波作为训练算法。调节器的特征是参数η的向量。我们的目标是通过最小化误差找到向量η的值,误差定义为: ei(k)=qdi(k)-qi(k) (11) 扩展卡尔曼滤波器的方法将估计向量的输出线性化[14],如下所示: (12) 式中: (13) (14) 式中,α1、α2为改变收敛速度的适应增益。 采用神经模糊系统来控制机器人的第1、第2和第3关节,优化各种输入/输出。它们表示输入的不同隶属函数的位置和形式,以及输出的增益。在这种情况下,开始时用遗传算法优化了6个参数,它们是模糊化的两个输入归一化增益(ai,bi),(其中(-ai,ai)或(-bi,bi)表示直线隶属度的限值)和每个分散调节器的一个解模糊输出增益。因此,对于标准调节器神经模糊型,将ai和bi的绝对值作为初始值。使用的编码类型为二进制编码。目标函数是整个轨迹上两个误差的绝对和。调节神经模糊控制如图3所示。 图3 机器人神经模糊控制优化 以机器人第3关节设置期望运动角位移为研究对象,通过仿真软件MATALAB测试遗传算法优化神经网络控制系统输出误差大小,并在仿真测试中添加负载。比较不同控制方法输出效果,分析机器人角位移输出误差,仿真参数如表1所示。 表1 仿真参数 假设机器人第3关节运动角位移为q(t)=cosπt/2,在无负载条件下,优化前和优化后的机器人运动关节角位移跟踪误差分别如图4和图5所示。在有负载条件下,优化前和优化后的机器人运动关节角位移跟踪误差分别如图6和图7所示。 在无负载条件下,图4和图5分别为优化前和优化后神经网络模糊控制效果,无论是优化前还是优化后,机器人第3关节角位移跟踪误差都较小,都能较好的跟踪期望角位移。在有负载条件下,图6和图7分别为优化前和优化后神经网络模糊控制效果,优化前,机器人第3关节角位移跟踪误差较大,容易受到负载的影响,控制系统精度较低。优化后,机器人第3关节角位移跟踪误差较小,能够抑制负载的影响,控制系统输出精度较高。因此,在相同条件下,对于具有不确定性的机器人轨迹控制,采用遗传算法优化神经网络模糊控制器,通过角位移误差输出反馈后,能够在线优化控制器参数,从而调整机器人运动轨迹,提高机器人抗干扰能力。 图4 优化前误差(无负载) 图5 优化后误差(无负载) 图6 优化前误差(有负载) 图7 优化后误差(有负载) 针对机器人关节运动角位移跟踪误差较大、容易受到负载干扰问题,设计了神经网络模糊控制器,利用遗传算法优化控制器参数,主要结论如下: (1)在无负载条件下,无论是采用优化前的神经网络模糊控制器,还是采用遗传算法优化后的神经网络模糊控制器,机器人运动关节角位移跟踪误差都较小,差别不大,都能够较好的实现机器人运动关节角位移的跟踪。 (2)在有负载条件下,采用优化前的神经网络模糊控制器,机器人运动关节角位移跟踪误差较大,调节控制参数能力较差,而采用遗传算法优化神经网络模糊控制器,机器人运动关节角位移跟踪误差较小,能够利用遗传算法优化控制器调整参数,从而快速调节控制器参数,达到降低误差的目的。
a3(t-t0)3t0
2 神经模糊控制器优化
2.1 遗传算法原理
2.2 神经模糊控制器
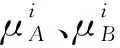


2.3 遗传算法优化控制器
3 误差仿真

4 结束语
