球头鼓锥形铣刀五轴加工刀刃切削区间分析*

赵志伟，郭明龙，魏兆成，王敏杰，舒 鑫，雍建华

(1.大连理工大学精密与特种加工教育部重点实验室，大连 116024；2.沈阳鼓风机集团股份有限公司，沈阳 110869)

0 引言

球头鼓锥形铣刀是一种可以高效高精度加工小曲率曲面的新型刀具，其侧铣加工时可以实现与曲面的线接触，能够将轨迹行距增大到2 mm，效率比球头铣刀高6倍以上。另一方面，球头鼓锥形铣刀刀刃可以设计成大螺旋角、大前角结构，有利于减小切削力、降低切削冲击，改善表面质量。

切削区间分析的目的是确定实际参与材料去除的刀刃区间，其与刀具几何、曲面几何、切深、步距、刀轴矢量和刀具轨迹等有关，加工过程中获得准确的刀具切削区间是力学与动力学研究的前提。目前，主要有实体建模法、离散法和解析法。

实体建模法是基于ACIS、UG、CATIA等软件，通过布尔求交运算获得切削几何接触，其计算精度极高，但仿真过程需要计算、保存和读取大量数据，计算效率较低。YANG等[1]通过可行接触面对去除材料体积进行修剪，不需要大量提取曲面及曲面交点就可获得刀-工接触面，提高了计算效率。BOZ等[2]将刀具沿轴向离散为一系列的切削层，通过建模软件将刀-工接触边界和二维圆盘图相交，获得每个切削层的切入角和切出角。ARAS等[3]将刀具与工件实体相交获得去除材料体积，将去除材料体积分解为面并与可行接触面相交获得刀-工接触边界。

离散法将工件和刀具几何特征划分为网格单元，进行离散化处理，计算效率高，但会造成计算精度的损失。LAZOGLU[4]离散工件和刀具为微小单元，对比切削刃离散点和工件网格节点的高度差判断该切削刃离散点是否与切削，从而获得刀刃接触区间。WEI等[5]通过逻辑数组区分刀-工接触区域和非接触区域。张臣等[6]基于Z-Map离散法，将刀具和工件的瞬时接触区域保存为数据点的格式，并将刀具刀刃进行离散，将离散的刀刃单元坐标与数据点进行比较判断该刀刃微元是否参与切削，最终确定参与切削的所有刀刃微元。ZHU等[7]通过离散的点向量描述工件曲面几何，比较刀刃微元点与点向量之间的距离以判断是否参与切削。

解析法是用数学表达式解析切削几何的接触，在能保证精度的条件下具有较高的计算效率。SUN等[8]利用已加工表面和待加工表面，迭代求解出刀刃参与切削的边界点。WANG、GENG等[9-10]沿刀轴矢量离散球头铣刀为一系列切削层，获得三轴加工中每一层的切入切出角，通过坐标旋转求解五轴加工刀具接触区域。WEI、GUO等[11-12]等针对曲面平头刀和球头刀五轴加工探索了基于降维映射的解析法分析切削几何，定义五轴加工的空间位置关系，并以其为新基底构建抽象二维空间，建立刀位点与空间点集的映射关系，进一步简化研究对象的维度，显著降低切削几何的研究复杂度。

球头鼓锥形铣刀作为一种非标刀具，没有成熟的产品，一般根据实际的加工用途进行设计、制造，薛帅[13]提出一种以加工条件为约束的球头鼓锥形铣刀轮廓数学模型。球头鼓锥形铣刀作为一种新型高性能刀具，相关切削力学与动力学研究尚未开展，由于其复杂的几何轮廓，刀刃接触区间的算法相较于传统的标准刀具如球头铣刀和平头铣刀等更为复杂。本文提出以空间约束条件确定刀刃切削区间的解析算法，可以准确快速的获得球头鼓锥形铣刀曲面五轴加工时的刀刃切削区间，为之后切削力学和动力学研究奠定了基础。

1 曲面五轴加工参数化定义

曲面五轴加工过程中，刀具的轨迹复杂，刀具和工件间的空间位置多变。这一复杂的工况，会大大增加用解析法确定刀刃切削区间的复杂程度。为降低计算的复杂程度，基于微分离散的思想，将刀具轨迹离散为一系列的刀位点，每个刀位点处近似为微小的斜平面五轴加工，如图1所示。

图1 曲面五轴加工参数化分析

为了进一步简化加工工况，准确描述加工时刀具与工件的空间位置关系，定义了工件坐标系、辅助坐标系和刀具坐标系以及进给方向角和刀轴倾斜角。

Ow-XwYwZw为工件坐标系，定义为刀具轨迹编程时的坐标系，在加工过程中保持不变。加工过程中的刀位点坐标、刀轴矢量和进给方向等信息都是基于该坐标系。

On-XnYnZn为辅助坐标系，定义原点On在球头鼓锥形铣刀刀头与刀杆分界面圆心位置，Zn轴为斜平面法向；Yn轴为刀具的瞬时进给方向，即一个刀位点和下一个刀位点的连线，位于斜平面内；Xn轴用右手坐标系原则确定。在辅助坐标系的视角下，斜平面五轴加工转换为平面五轴加工，进一步简化了加工工况。

Oc-XcYcZc为刀具坐标系，定义原点Oc在球头鼓锥形铣刀刀头与刀杆分界面圆心位置，Zc轴为沿刀轴背离刀尖的方向；Xc轴由辅助坐标系Zn轴和刀具坐标系Zc轴叉乘获得，因此Xc轴位于On-XnYn平面内；Yc轴由右手坐标系原则确定。

进给方向角kf定义为刀具坐标系的Xc轴和辅助坐标系Yn轴之间的夹角，用于表示刀具相对于进给方向的偏转角度。

刀轴倾斜角ka定义为刀具坐标系的Zc轴和辅助坐标系的Zn轴之间的夹角，用于表示刀具相对于工件法向的倾斜程度。

空间中的任意一点在辅助坐标系下的坐标(xn,yn,zn)和刀具坐标系下的坐标(xc,yc,zc)之间可以通过下式转换：

(1)

式中，M1、M2为转换矩阵，分别为：

2 球头鼓锥形铣刀刀刃曲线表达式

建立刀刃曲线的数学表达式是通过解析法分析刀刃切削区间的基础。球头鼓锥形铣刀轮廓模型如图2所示，其中包括球头部分半径r，mm；鼓锥形部分半径R，mm；刀头长度l，mm；刀头顶部直径d，mm；最大侧倾角α同时定义刀具轮廓上任意一点与刀头顶部圆心连线和刀具轴线之间的夹角为轴向位置角k，取值范围为(0，90°)。

图2 球头鼓锥形铣刀刀头部分轮廓参数

本文该轮廓模型基础上，建立常见的等导程螺旋刃表达式。等导程螺旋刃是指在刀具旋转一周时，刀刃上的任意一点沿轴向的移动距离相同。球头鼓锥形铣刀从底部到顶部，回转半径逐渐增加。球头鼓锥形铣刀的球头部分和鼓锥形部分的回转半径变化规律不同，因此需要用不同的表达式分别表示。两部分的分界点对应的轴向位置角为k0，当k∈(0,k0)时，刀刃曲线位于球头部分上，当k∈(k0,π/2)时，刀刃曲线位于鼓锥形部分上。

(1)球头部分刀刃曲线。球头部分第j条刀刃曲线的表达式为：

(2)

式中，β为该刀刃微元点与球心的连线和刀轴之间的夹角，其表达式为：

(3)

θz为该点的径向位置角θ相对于刀刃起点处的径向位置角θ0的滞后角度，其表达式为：

(4)

式中，N为刀具的刀刃数量；η为刀刃曲线的螺旋角。

(2)鼓锥形部分刀刃曲线。以鼓锥形部分刀刃曲线上任意一点P和刀轴为平面建立图3所示的平面坐标系O-XY，L为鼓锥形曲线在P点处的切线，则该点满足的几何关系为：

(5)

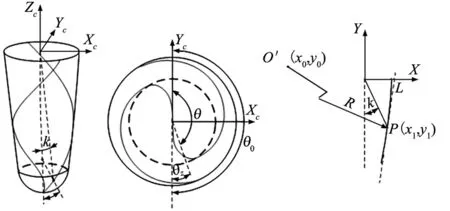
图3 球头鼓锥形铣刀刀刃曲线几何分析

式中，(x0,y0)为鼓锥形轮廓曲线的圆心坐标。

式(5)可以求出该点在平面坐标系O-XY下的坐标(x1,y1)，则该点在刀具坐标系下坐标为(x1sinθz,x1cosθz,y1)。整理可得鼓形部分第j条刀刃曲线的表达式为：

(6)

式中，

(7)

3 刀刃切削区间分析

刀刃的切削区间是指切削过程中实际参与材料去除的刀刃范围。本文提出一种名为空间约束法的解析算法，可以直接计算刀刃切削区间，不需要计算刀具和工件的接触区间，因此算法简洁清晰，计算效率高。图4为球头鼓锥形铣刀平面五轴加工。

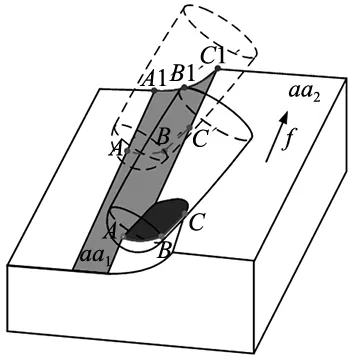
图4 平面五轴加工的空间约束条件

将刀刃曲线离散化，则刀刃微元参与切削时应满足3个空间约束条件：进给方向下，刀刃微元应在已加工面和待加工面交线ABC之前；刀刃微元应该在前一条刀具轨迹扫掠面aa1之外；刀刃微元应在待加工平面aa2之下。

遍历刀刃的所有刀刃微元，可准确的计算出刀刃的切削区间的上界点对应的轴向位置角ku和下界点对应的轴向位置角kd。

(1)空间曲线ABC。将空间曲线ABC视为一系列的点组成，则每个点应满足的条件为：在辅助坐标系下，刀具轮廓上所有Xn轴坐标值相同的点中Zn轴坐标值最小的点，所以空间曲线ABC可以通过极值定理计算。

假设xn=a，其对应的刀具轮廓上的极小值点可以通过拉格朗日乘子法求出：

minF(x,y,z)=-ysinka+zcoska

(8)

约束条件为：

①该点应该在刀具轮廓上，其中位于球头部分轮廓上表达式为：

x2+y2=r2-(r-z-l)2

(9)

位于鼓锥形部分轮廓上表达式为：

(10)

②刀具坐标系下刀具轮廓上的点转换到辅助坐标系下应满足xn=a，表达式为：

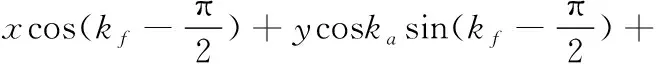
(11)

辅助坐标系下刀刃微元点坐标(xn,yn,zn)，通过式(5)求出该点对应的空间曲线ABC上的点(xn,ymin,zmin)，该点参与切削时必须满足的条件为：

yn≥ymin

(12)

(13)

(3)待加工平面aa2。如图5所示，在辅助坐标系下，待加工平面aa2距辅助坐标系原点的距离为h，有几何关系可知：

h=(l-r)coska+r-dn

(14)

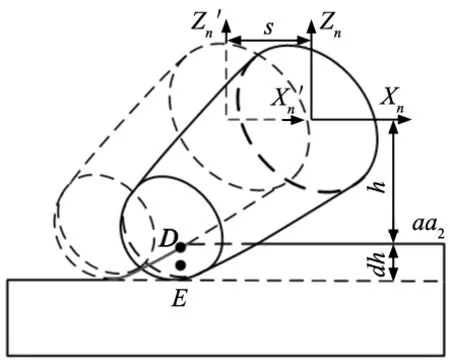
图5 平面切削时几何关系示意图

式中，dn为切削厚度。

刀刃微元参与切削时，必须满足的关系式为：

zn≤-h

(15)

综上所述，刀刃微元点参与切削时，必须满足的3个关系式为：

(16)

(4)算法流程。基于微分离散的思想，将刀刃曲线的轴向位置角k为等分为n份，每一个刀刃微元对应的轴向位置角为ki(i=1,2…n)，获得每个ki对应的刀具坐标系Oc-XcYcZc下的坐标(xci,yci,zci)，再由式(1)进行空间旋转变换，得到辅助坐标系On-XnYnZn下的坐标(xni,yni,zni)，利用式(16)的判断条件判断刀刃微元是否参与切削。

从刀刃起点处(i=1)开始，沿刀刃曲线逐个判断每个刀刃微元点是否参与切削，直到找到两个连续的刀刃微元点，ki参与切削且ki-1不参与切削，则切削区间的下界点kd就位于这两个刀刃微元点之间。沿着刀刃曲线继续寻找，直到找到两个连续的刀刃微元点，ki不参与切削且ki-1参与切削，则切削区间的上界点ku就位于这两个刀刃微元点之间。具体流程如图6所示。

图6 空间约束法算法流程图

为了提高计算效率，刀刃曲线的轴向位置角k离散的步距Δk较大，获得的连续的两个刀刃微元点ki和ki-1之间的差值较大。对于获得的刀刃上界点区间和下界点区间，需要通过黄金分割法进行精确计算，以获得准确的上界点和下界点。通过设置的允许误差Δe，可以控制求解精度，Δe值越小，求解精度越高。以寻找刀刃切削区间下界点kd为例，算法流程如图7所示。

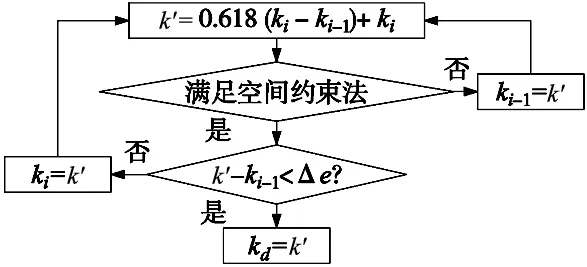
图7 黄金分割法算法流程图

将刀具的径向位置角依次增加2jπ/N，可以计算出刀具所有刀刃的切削区间。将旋转位置角按[0,2π]离散，重复进行上述的算法流程，可以求出刀具旋转一圈时，一条刀刃在各个旋转角下的切削区间。

4 刀刃切削区间仿真

实体建模法作为计算切削区间的一种方法，虽然效率比较低，但可以认为是绝对精确的，因此将实体建模法作为验证空间约束法求解精度的标准。利用Unigraphics NX建模软件分别仿真了斜平面和叶片曲面五轴加工时的刀刃切削区间，并与空间约束法求出的刀刃切削区间进行了对比验证。

(1)斜平面五轴加工。设置的刀具参数和加工参数如表1和表2所示。

表1 平面五轴加工中刀具参数和切削参数

表2 平面五轴加工中切削参数

在Unigraphics NX中建立斜平面模型，并通过布尔运算减去前一条刀具轨迹切除的体积。随机选取1个刀位点，在刀位点处按照刀具参数生成刀具模型。工件模型和刀具模型布尔运算求交可以获得刀具和工件的接触区域。基于空间约束法，计算出刀具旋转一周时，刀刃切削区间的上界点和下界点，并且导入到工件模型中，刀刃切削区间的上下界点全部位于刀具-工件接触区域的边界线上，其中红点为上界点，蓝点为下界点，如图8所示。

同时在刀具旋转位置角20°、70°、100°、130°、180°、220°、255°、280°、320°、350°处添加刀刃曲线，即获得实体建模法求出的刀刃切削区间的上下界点。两种方法的求解结果对比如图9所示，其中k0线为球头和鼓锥形部分刀刃微元点径向位置角分界线。两种方法获得的切削区间上下界点完全相同，证明了空间约束法计算的斜平面五轴加工刀刃切削区间具有绝对的精度。

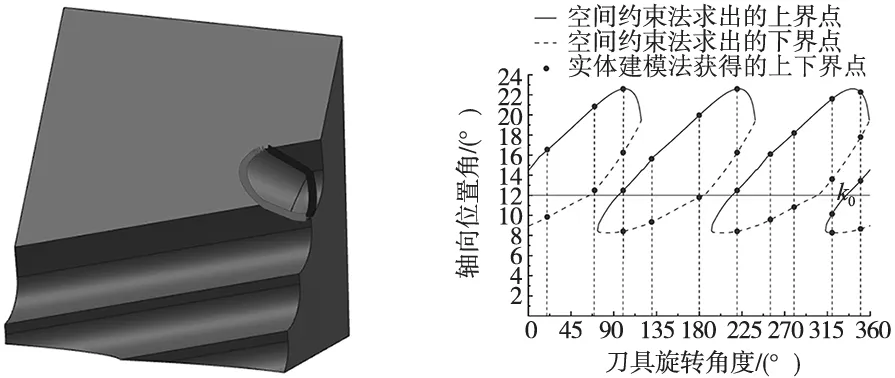
图8 空间约束法求得的切削区间上下界点验证 图9 斜平面五轴加工刀刃切削区间仿真结果对比

使用实体建模法获得刀刃切削区间时，运算过程中需要进行大量的建模和布尔运算，效率十分低下。并且获得刀具旋转一周时，各个旋转位置角下的刀刃切削区间则需要进行大量的重复操作或者对软件进行二次开发。而本文提出的空间约束法，在个人的i5处理器、8 G运行内存的计算机上进行计算上述实例时，仅仅花费5.4 s，便可获得刀具各个旋转位置角下的刀刃切削区间，在效率上比实体建模法有显著的优势。

(2)叶片曲面五轴加工。为检验提出的空间约束法在曲面五轴加工中的精度，安排了叶片曲面五轴加工仿真，安排的刀具参数同表1，切削参数如表3所示。

表3 叶片曲面五轴加工中切削参数

图10 叶片曲面五轴加工三维建模

在Unigraphics NX建立叶片模型，刀具轨迹通过叶片的边界曲线生成。布尔运算减去前一条刀具轨迹切除的体积。沿刀具轨迹选取4个刀位点，在每个刀位点处按照刀具参数生成刀具模型，叶片模型和刀具模型布尔运算求交可以获得刀具和工件的接触区域。

在刀位点1处按照刀具旋转角度30°、45°、60°、75°、140°、155°、170°、185°、295°、310°、325°、340°生成刀刃曲线，刀刃曲线与刀具-工件接触区域边界的交点即为刀刃切削区间的上下界点，通过测量角度工具即可获得上下界点的轴向位置角。基于前面提出的空间约束法，求解出刀具旋转一周时，三条刀刃切削区间的上下界点。刀位点1处叶片曲面五轴加工刀刃切削区间仿真结果的对比如图11所示。

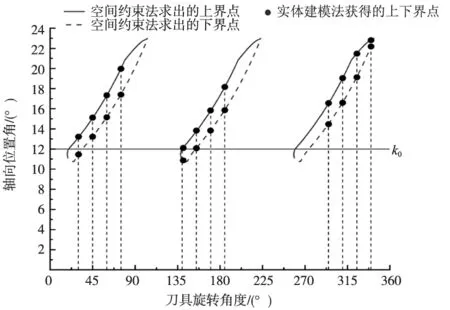
图11 刀位点1处叶片曲面五轴刀刃切削区间仿真结果对比

分别求出4个刀位点处，刀具旋转角度为30°、45°、50°、75°时刀刃切削区间的上下界点，空间约束法的求解精度如表4所示。

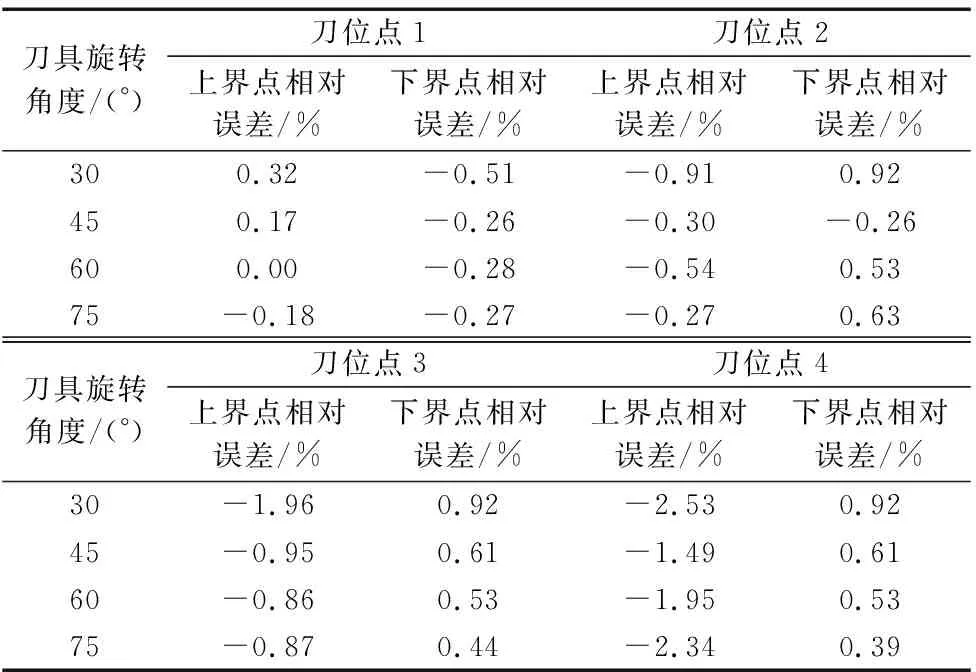
表4 空间约束法在叶片曲面五轴加工中的求解精度

空间约束法在求解叶片曲面五轴加工时存在误差，其主要原因是该方法基于微分离散的思想将曲面近似为斜平面加工，但实际上刀位点处的曲面并不是绝对的斜平面，曲率增大会降低计算精度。但球头鼓锥形铣刀主要用于加工小曲率曲面，因此误差不超过3%，对于切削力学以及切削动力学建模的影响较小，几乎可以忽略不计，同时可以提高径向位置角的离散精度、降低允许误差的值等方法提高计算精度。总之，仿真的结果证明了空间约束法在计算曲面五轴加工切削区间上的应用是完全可行的。

5 结束语

根据新型球头鼓锥形铣刀轮廓模型，建立等导程螺旋刀刃曲线的表达式。针对小曲率曲面加工中复杂的工况，基于微分离散的思想，将曲面加工离散为一系列的斜平面加工。对斜平面加工参数化定义，通过辅助坐标系将斜平面加工转换为平面加工，通过刀轴倾斜角和进给方向角表示刀具与工件和进给方向的位置关系，降低了曲面五轴加工切削区间分析的复杂程度。

基于空间几何，提出一种解析计算刀刃切削区间的算法。构建出空间约束条件对所有刀刃微元逐一判断是否参与切削，以确定整个刀刃切削区间的上下界点。安排了实体建模法的斜平面和叶片曲面五轴加工仿真，对比结果表明：空间约束法在平面五轴加工切削几何分析中具有绝对的精度，在叶片曲面五轴加工切削几何分析中虽然有一定的误差，但最大误差不超过3%，对于切削力学和动力学建模的影响是在可接受的范围内。并且空间约束法的计算效率比实体建模法大大提高，能同时兼顾效率和精度，并且可以降低生产成本。