低码率信道编码后加扰的码分多址特性分析
2022-09-27宋庆军
石 荣,宋庆军
(电子信息控制重点实验室,四川 成都 610036)
0 引言
在传统通信过程中使用扰码对传输码流进行加扰主要是为了增强码流的随机性,一方面避免发射端码流中相同码字的连续重复出现,不仅使得信号的短时功率谱分布更加均匀,以满足相关通信标准的要求,而且也有利于通信接收端实施符号定时的恢复[1];另一方面,扰码通常由通信收发双方共同确定,一般不会主动向第三方透露,经过发射端加扰的码流只有掌握扰码的接收端能够成功解扰,处于非合作状态的第三方由于不知道扰码序列而难以解扰,进而也无法对截获的码流进行后续的处理,所以扰码在一定程度上能够发挥与密码类似的信息保密功能[2-4]。在现代的4G/5G移动通信系统中广泛使用扰码来增加传输码流的随机性[5-6],而且扰码序列的产生与基站小区ID(Identity)、用户的临时身份标识、传输时频资源块的编号等信息紧密关联,使得不同小区、用户、时隙等条件下扰码也不同[7-8];由于小区间使用的扰码序列不同,解扰过程中还可以在一定程度上缓解同频小区之间的互扰问题。
受上述扰码应用方式的启发,本文通过分析后发现各个不同的用户使用相同的信道编码器实施低码率信道编码之后,采用不同的扰码序列进行加扰,能够达到多用户码分多址同时同频传输的目的。为了构建码分多址通信系统更加通用的理论模型,本文从硬比特编码空间与软比特解码空间分别对相关技术原理进行了分析,并采用该技术原理的特殊示例,即重复码信道编码后加扰的模型对传统直接序列扩频通信的码分多址特性进行了重新阐释,然后从软比特解扰与最大似然译码的角度构建了一个统一的框架模型,将多用户码分多址传输、多用户互扰分析等纳入到了统一的模型之中。最后通过选取典型编码参数开展了仿真,验证了相关分析的有效性与正确性。
1 低码率信道编码与加扰传输
信道编码的码率R越小,其纠错能力也越强,但为了便于工程实现,R也不能取值过小。在DVB-S2标准中最低码率为1/4[9],在DVB-S2X标准中最低码率为1/5[10],在4G移动通信的物理控制格式指示信道(Physical Control Format Indicator Channel,PCFICH)中采用了1/16码率的编码[11]。由此可见,工程应用中信道编码的码率一般在1/20以上[12],当然低码率的下限没有一个统一的准则,在有关信道编码的文献中最低码率的理论取值也曾达到1/100[13],为了便于分析,本文将信道编码的低码率暂且限定在1/20≤R≤1/4范围。
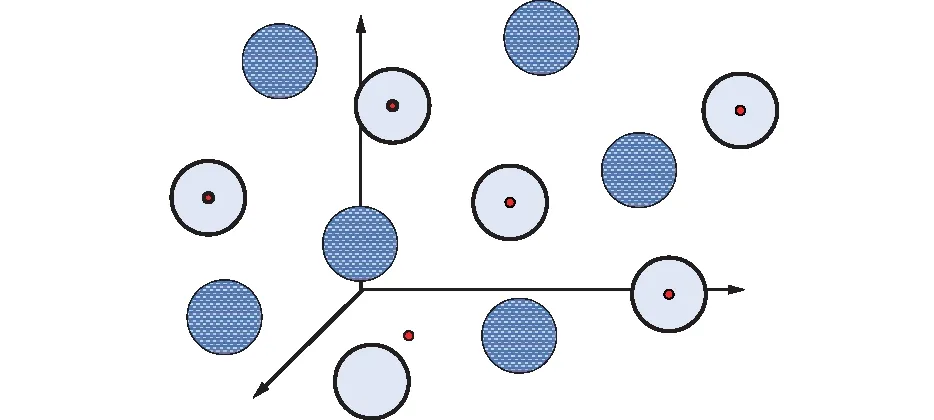
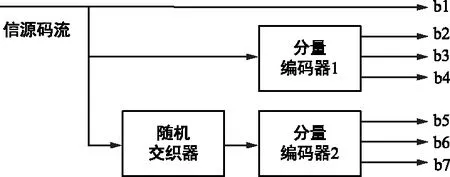
以工程上常见的(n,k)分组码为例,k比特信源数据码流Cd(i),i=1,2,…,k,在经过码率为R(0 n=k/R。 (1) 对码流Cc(j)进行加扰,扰码Csc(j)的长度同样为nbit,生成的码流Ctr(j)向接收端发送: Ctr(j)=Cc(j)⊕Csc(j), (2) 式中,⊕为模二加运算符。在接收端解调出0/1比特流之后,通过同样的扰码Csc(j)实施解扰,即 Ctr(j)⊕Csc(j)=Cc(j)。 (3) 在此基础上对Cc(j)进行信道译码,从而恢复出码流Cd(i)。上述解扰译码过程是从硬判决信道译码的角度来描述的,在实际应用中为了提升接收性能,接收端往往采用软判决信道译码,即通信接收端的解调器输出每一比特rj取1和0的概率之比的对数,记为Sre(j),称为软比特,表达为: Sre(j)=ln(P(rj=1)/P(rj=0)), (4) 式中,P(·)表示概率函数。对于软比特的解扰可采用式(5)完成: Saf(j)=Sre(j)×(1-2Csc(j)), (5) 由式(5)可见,软比特解扰之后仍然为软比特。在此基础上对解扰之后的n个软比特Saf(n)进行软判决信道译码,从而最终恢复出k比特信源码流Cd(i),整个通信传输过程如图1所示。 图1 低码率信道编码与加扰传输原理框图 对于上述整个收发过程,表面上看不出有任何特别之处,但接下来将上述过程放置在多用户应用场景中,就能体现出低码率信道编码与加扰组合应用的特点所在,继续分析如下。 在伽罗华域G(2)上,k个信源0/1比特构成了信源码字空间Ssrc,该空间一共有2k个码字。信道编码之后的空间称之为编码空间Scd,该空间中一共有2n个码字,但其中仅有2k个码字是无误比特的码字。由于编码码率R较小,由式(1)可知:n≫k,所以无误比特的码字数量占整个编码空间Scd中码字数量的比例非常小,仅占2k-n,如果从整个编码空间来看,无误比特的码字分布非常稀疏。 码字的纠错能力与具体的编码方式有关,由编码理论可知:对于最小距离为dmin的线性码能够纠正所有含不大于(dmin-1)/2个错误比特。假设该信道编码中每n个编码比特可纠正Ne个随机比特错误。对于单个用户来说,在编码空间中以各个无误码比特的码字为中心点,形成半径为Ne个比特的2k个子区域。由于编码空间是伽罗华域G(2)上的空间,与传统欧式空间不一样,所以此处的距离以差异比特的数量来描述,即汉明距。如果用三维欧式空间作一个比拟,则相当于围绕这些无误码码字为球心的小球散布于整个编码空间之中,小球的大小反映了纠错能力,在这些小球外部的区域则是该译码方法无法纠正错误的码字区域,如图2所示。 图2 对编码空间硬判决译码的码字纠错能力示意图 将上述能够成功完成硬判决译码的子空间记为Ssubc,Ssubc仅占整个编码空间Scd中的一小部分。假设两个用户使用同一个信源码字空间Ssrc,在信道编码之后采用两个不同的扰码Csc1(j)和Csc2(j)对编码后的码字进行加扰,则等效于将Ssubc进行不同方向的位移,并记位移之后的两个子空间分别为Ssubc1和Ssubc2,只要二者满足式(6),即二者没有交集,则能够确保两个用户码字的共存。 Ssubc1∩Ssubc2=∅, (6) 式中,∅表示空集。如果用三维欧式空间作一个比拟,则相当于上述两个用户的可纠正误码的码字空间小球在整个空间中都是不重叠的,如图3所示。图3中两种不同图案的小球分别代表不同的用户所占据的编码子空间。 图3 两用户信道编码后加扰在空间中共存示意图 由图3可知,两用户在信道编码后加扰所形成的两个子空间Ssubc1和Ssubc2是否相交,不仅取决于两个不同的扰码序列Csc1(j)和Csc2(j),而且同样取决于信道编码后码字的最小距离为dmin,dmin越小,两个子空间越不容易相交。由于dmin与信道编码的纠错能力直接相关,所以两个用户之间的共存特性可通过选择具有不同纠错能力的信道编码器来进行调节。将上述两个用户的分析结论推广至多用户的应用场景,那么在编码空间中多用户共存的码分多址特性也就自然形成了。 在信息码流从发送端到达接收端的过程中加入了信道引入的各种噪声,在接收端采用软判决译码时,解调器输出的软比特连续取值,其所构成的解码空间可以看成欧式空间。对比编码空间与解码空间即可发现,编码空间中各用户对应的有效码字取值范围是一个个离散的点,如果将编码空间中的比特1映射成+LP,比特0映射为-LP,其中LP是一个与该信号的比特能量信噪比相关的参数。那么解码空间中各用户对应的有效码字取值范围是以编码空间中该用户的等效有效码字点为中心的一个个连续的区域范围,而区域大小是由设定的译码错误概率所决定的,这一特点用图3来类比也是合适的。如此一来,编码空间与解码空间之间的对应关系也可以随之建立。 如图3所示,不同用户的码字有效取值范围占据了整个空间中的不同区域。如果两个用户在解码空间中所占有的有效区域互不交叠,分别对应了前述的子空间Ssubc1和Ssubc2;且解调器输出的软比特按照式(5)采用第一个用户的扰码Csc1(j)进行解扰,解扰结果就相当于在解码空间中将子空间Ssubc1逆向位移转换成了子空间Ssubc。于是解扰后待译码的软比特与第一个用户当前真实码字Cc1(j)的距离应该最小,采用最大似然译码即可得到第一个用户真实码字的估计值。而在这一过程中解调器输出的软比特中所包含的第二个用户的信息,在解扰过程中所使用的扰码并不是自身对应的扰码Csc2(j),这样的操作意味着子空间Ssubc2并没有被移回到Ssubc中,所以原有信息码流不能被恢复。如果从硬比特的视角来看待这一过程,即等效于对第二个用户的当前码字Cc2(j)进行了如下操作: Cc2(j)⊕Csc2(j)⊕Csc1(j)=Cc2(j)⊕Csc,new(j)≠Cc2(j), (7) 式中,两个用户的扰码Csc1(j)和Cc2(j)模二加之后产生了一个新的扰码Csc,new(j),这使得解调器输出的软比特解扰后待译码的软比特不仅与第二个用户当前真实码字的距离较大,而且与子空间Ssubc中除Cc1(j)之外其他有效码字的距离也较大,从而在最大似然译码过程中并不占优,所以对使用扰码Csc1(j)进行软比特解扰之后进行最大似然译码,最终的译码结果即是第一个用户当前真实码字Cc1(j)。同理,如果解调器输出的软比特按照式(5)采用第二个用户的扰码Csc2(j)进行解扰,上述过程对两个用户的作用效果就会反过来,最终的译码结果即是第二个用户当前真实码字Cc2(j)。 由上述对低码率信道编码后加扰传输的编解码过程的解释可知:不同的用户通过不同的扰码在编码空间与解码空间中进行区分,这也体现了码分多址的特性,于是采用该方法进行m个用户的码分多址通信传输的原理如图4所示。 图4 m个用户码分多址通信传输原理框图 如图4所示,整个编解码空间所能容纳的用户数量由哪些因素决定呢?这与各个用户所使用的扰码序列之间的相关性紧密关联。由前述过程可知,整个空间中所能容纳用户的数量与各用户占有的子空间Ssubc紧密相关。Ssubc越大,整个编解码空间所能容纳的用户数量就越少;相反,Ssubc越小,用户数量越大。以(n,k)分组码编码为例,在编解码空间比特数n保持一定的情况下,码率R越低,Ssubc越小,整个编解码空间所能容纳的用户数量越多。 利用前述已经建立的多用户码分多址通信传输模型来重新解释传统直接序列扩频通信的码分多址特性,从而构建一个统一的框架模型,以便反映更加普遍的原理。 传统直扩通信的码分多址模型是通过不同用户采用不同扩频码的扩频解扩来实现的。在通信发射端用扩频码序列对数据码进行扩频处理,且扩频码速率是数据码速率的Rdsss倍,一般Rdsss为正整数。如果从数字信号处理的角度来说,按照扩频码速率进行采样,则一个扩频码码片对应一个0/1比特数据,记扩频码序列为Cchip(ic),ic=1,2,…,Rdsss,数据码仅有1 bit,记为Dda。该数据码按照码率R=1/Rdsss的重复码进行编码,编码之后的码字序列记为Ccd(ic),且 Ccd(ic)=Dda。 (8) 对编码后的码字Ccd(ic)与扩频码序列Cchip(ic)进行模二加后得到码流Ctr,ds(ic): Ctr,ds(ic)=Ccd(ic)⊕Cchip(ic)。 (9) 将码流Ctr,ds(ic)中的1 bit映射为+1,0 bit映射为-1,进行调制后发射即完成了通信发射端的直接序列扩频过程。上述重复码编码过程是一个典型的低码率信道编码过程,如果把扩频码序列Cchip(ic)看成一个扰码序列,将式(9)与式(2)进行对比可知:直接序列扩频发送过程就是一个典型的低码率信道编码后加扰的发送过程。 传统通信理论指出:直接序列扩频通信是一个典型的码分多址系统,不同用户采用不同的扩频码作为地址码来进行区分。同样类比,如果将不同用户的扩频码看成是他们各自不同的扰码序列,同样能够用图4所示的低码率重复码编码后加扰传输模型来解释直扩通信中多用户共存的特性。 在直接序列扩频通信的接收端,将接收到扩频信号变频至基带,按照扩频码速率进行采样并完成码流同步之后,所得到的基带信号序列记为Sbase(ic),用本地扩频码序列Cchip(ic)按照下式与Sbase(ic)相乘进行解扩,所得信号Sdds(ic)如下: Sdds(ic)=Sbase(ic)×(1-2Cchip(ic))。 (10) 直扩信号的后续解扩过程可以采用对Rdsss个采样值求和后判决的方法来实现,即 (11) 对比式(10)与式(5)可知:直扩信号的解扩过程与前述加扰信号的解扰过程能够完全对应,二者所具有的多用户区分作用也是相似的。而对于解扩过程中的判决式(11),完全可以看成是重复码编码的软比特译码过程。如此一来,上述直接序列扩频的接收过程同样是一个典型的低码率信道编码后加扰传输的接收过程。 综上所述,直扩通信中不同用户采用不同的扩频码来进行区分,一个确定的直扩系统中所能容纳的用户数量也是一定的[14]。在直扩接收端使用某一个用户的扩频码对信号实施解扩,即可获得该用户对应的码流,采用前述的不同用户码流软比特解扰后,再进行软判决信道译码来区分多用户的模型同样是能够解释的。这也说明了低码率信道编码后加扰传输的新模型具有更加广阔的适用范围。 采用当前最常用的两种信道编码LDPC码与Turbo码作为仿真对象。其中LDPC码直接采用DVB-S2通信标准中1/4码率的长码;Turbo码参照文献[15]中的Turbo码分量编码器进行设计,码率为1/7,如图5所示。 (a) Turbo编码器 图5中信源码流每输入1 bit,Turbo编码器输出7 bit,其中第1比特为系统比特,两个分量编码器分别输出3 bit。随机交织器的大小为100 bit,每个分量编码器从零状态开始,在完成100 bit的编码之后,还需要输入3个收尾比特以返回零状态,在收尾比特输入时编码器也会输出相应的校验比特。所以该Turbo编码器每输入100 bit的数据后进行编码,最后会输出编码后的724 bit(包含两个分量编码器的收尾比特)。 在LDPC编码应用下,不同用户的信源16 200 bit按照1/4码率编码后生成64 800 bit,参照图4,不同用户按照不同的扰码对64 800 bit进行加扰,加扰后的码流使用BPSK调制方式进行传输。在Turbo编码应用中,不同用户的100 bit数据在经过1/7码率编码后为724 bit,参照图4,不同用户按照不同的扰码对724 bit进行加扰,加扰后的码流同样使用BPSK调制方式进行传输。 在一个多用户通信系统中不同用户的信号是以相同的频率和速率同时进行信道传输的。在此以5G通信标准中常用的两个扰码序列为例进行仿真,其生成多项式分别为: x1(ns+31)=x1(ns+3)⊕x1(ns), (12) x2(ns+31)=x2(ns+3)⊕x2(ns+2)⊕ x2(ns+1)⊕x2(ns), (13) 式中,ns为序列的序号,初始值x1(1)=x2(1)=1,当ns=1,2,…,30时,x1(ns)=x2(ns)=0。显然式(12)和式(13)中的扰码长度为231-1,对于64 800 bit与724 bit长度的码流,从其中截取一段进行加扰即可。 通信接收端在BPSK解调之后按照每比特数据采样一个点,输出软比特,使用不同用户的扰码按照式(5)进行软比特解扰后,都采用对数MAP算法进行迭代译码,在两个用户的信号具有相同的幅度的条件下,译码过程中信道可靠性因子参数中的Es/n0取值为1,经过1 000次蒙特卡洛仿真,仿真结果表明:分别解扰之后的软判决译码100%能够分别获得两用户无误码的原始码流,从而成功验证了低信道编码后加扰的多用户码分多址特性。 从原理上讲,在两个用户的地址码不能完全正交时一定会产生多址干扰。在低码率信道编码后加扰的过程中,两个扰码并没有经过特殊设计,正交性无法保证,所以该方式下的码分多址应用大多存在多址干扰,即存在大信号压制小信号的情况,且小信号用户能承受多址干扰的大小与码率是紧密相关的。码率越小,小信号用户能够承受大信号用户的干扰越强,图6是两用户的信号幅度在不同比例条件下,小信号用户译码后的误比特率变化的仿真曲线。 图6 在大信号用户多址干扰下的小信号译码正确率 由图6可见,在1/4码率的LDPC编码后加扰的两用户系统中,当大/小信号幅度比≤1.3,即大信号能量不超过小信号能量的1.69倍时,小信号能够实现无误码的译码;在1/7码率的Turbo编码后加扰的两用户系统中,当大/小信号幅度比≤1.6,即大信号能量不超过小信号能量的2.56倍时,小信号能够实现无误码的译码。当大/小信号幅度比超过上述数值时,无论是LDPC码还是Turbo码,小信号的译码平均误码率随大/小信号幅度比值的增大而增大。该仿真结果也反映出,1/7码率比1/4码率更低,所以该小信号用户能够承受大信号用户干扰的能力也更强。作为对比,两个采用7 bit长度的扩频码的码分多址系统,扩频序列分别为:0010111和0100111,这两个扩频序列的互相关最大值可达到5,而最大自相关值为7。该扩频码分多址系统中当大/小信号幅度比超过1.4时,同样会出现大信号干扰小信号的情况,因为可以用重复码信道编码后加扰的模型来解释直扩码分多址系统。上述对比结果也说明了通过低码率信道编码后加扰的方式来构建码分多址通信系统的有效性与普适性。如果将该思想向更加广阔的应用领域进行扩展,在文献[16]提出的基于广义加扰的时域压缩扩频抗干扰能力增强方法中也有上述思想的部分体现,大家可以对照体会。 本文在对低码率信道编码后加扰传输的收发端编解码处理流程与方法简要介绍的基础上,分别从编码空间与解码空间对该通信传输方式的多用户码分多址特性进行了分析,并利用该特性以重复码编码后的加扰处理重新解释了传统直接序列扩频通信的码分多址特性,从而构建了一个码分多址系统的统一框架模型。最后通过码率为1/4的LDPC码与码率为1/7的Turbo码为例开展了仿真实验,仿真结果验证了前述分析的正确性与有效性,从而为码分多址通信系统的理论建模与特性分析提供了另一个视角的理解。该通用模型不仅向下兼容传统直扩CDMA模型,而且还能够为当前大量使用加扰处理的地面移动通信系统的互扰特性分析提供新的方法与途径,这对于码分多址通信系统的全新设计与性能进一步提升具有重要参考意义。
2 在编码空间用不同扰码区分用户

3 解码空间中解扰后的信道译码

4 用重复码加扰解释直扩码分多址特性
5 仿真验证

6 结束语
