直流式迷宫调节阀流道降压流动特性及临界空化预测
2022-09-26金浩哲段奥强刘骁飞王超
金浩哲,段奥强,刘骁飞,王超
(浙江理工大学机械与自动控制学院,浙江 杭州 310018)
调节阀在工业介质输送过程中起调节介质压力与流量的作用,是现代工业自动化系统中确保各种工艺设备正常运行的重要装置[1].其中,迷宫式压力调节阀相对于其他阀门具有高降压、高速流的特点,其阀芯碟片上的迷宫流道是产生降压的核心元件,广泛地应用于电力、煤化工、冶金等工况环境恶劣的能源行业中,严苛多变的工况压力易使其出现闪蒸空化汽蚀现象[2].空泡溃灭时的爆破力将会使碟片上的流道遭受极其严重的损伤,导致泄漏,影响流量控制精度的同时,严重威胁机组装置正常的安全运行[3].因此,无论是从迷宫阀灵敏度、精准度上,还是从机组装置的可靠性、安全性角度,工程上都会竭力避免空化现象[4].
国内外许多专家、学者及工程人员对迷宫阀的降压特性、流动特点和空化机理进行了深入的研究.WANG等[5]针对串并联组合的迷宫流道进行数值模拟得到串联通道主要降压、并联通道主要调节流量的结论.范利霞等[6]通过数值模拟得出角质迷宫阀级数越多降压越平稳,并结合理论分析推导出适用于蒸汽工况的级数理论计算公式.董学莲等[7]通过CFX数值模拟了不同尺寸下迷宫流道的降压流动特性,并提出基于分流和对冲相结合的迷宫流道.
目前大多数学者主要针对迷宫阀的流动特性、降压机理等方面进行研究,设计新型流道、改进流道尺寸、增添辅助装置避免空化现象[8].但关于迷宫阀阀芯流道级数的临界降压值与空化的关系研究相对较少,而在迷宫阀的实际应用中又急需不同流道级数下临界空化降压值的基础规律性研究.因此文中以是否空化为前提,通过数值模拟方法对迷宫流道临界空化降压值进行基础规律性研究,从而改进优化流道的结构设计,选择合适的工况压力和流道级数,从根源上避免闪蒸空化汽蚀.
1 几何模型和数值模型
1.1 模型描述和网格划分
图1为直流式迷宫阀结构示意图,主要由阀体、节流阀座、迷宫碟片阀芯、阀盖、阀杆、法兰、法兰盘和节流孔板等零部件组成.曲折的直流式迷宫流道均匀地分布在迷宫碟片上.迷宫阀技术指标:介质为水,温度为250 ℃,压差大于等于10.7 MPa,口径为350 mm.
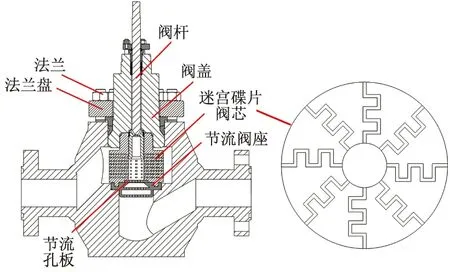
图1 直流式迷宫阀结构示意图Fig.1 Structure diagram of straight flow labyrinth valve
根据技术指标要求单个迷宫流道所能承受的最低压力为0.5 MPa.这是因为迷宫阀的降压主要集中在迷宫流道内部,单个直流式迷宫流道的特性在一定程度上能够表征整体迷宫阀的特性;另外空化模型需要高质量低扭曲率的网格,整个迷宫阀结构复杂,划分后的网格质量难以满足空化模型的要求.综合考虑,选择研究单个直流式迷宫流道的降压、流动和空化特性.
使用Solidworks建立二级、四级、六级、八级直流式迷宫流道的流体域,流道尺寸与实际迷宫流道尺寸完全相同,流道每一次直角转折代表一级.使用ICEM进行正六面体结构网格划分,如图2所示.网格节点数为43万,网格质量皆在0.9以上.增加一倍和两倍的网格节点后,Y=52 mm截面处中心线X的速度v基本相同,如图3所示.排除网格质量、数量对模拟计算结果的影响,其他级数迷宫流道的网格划分结果与八级流道相同.
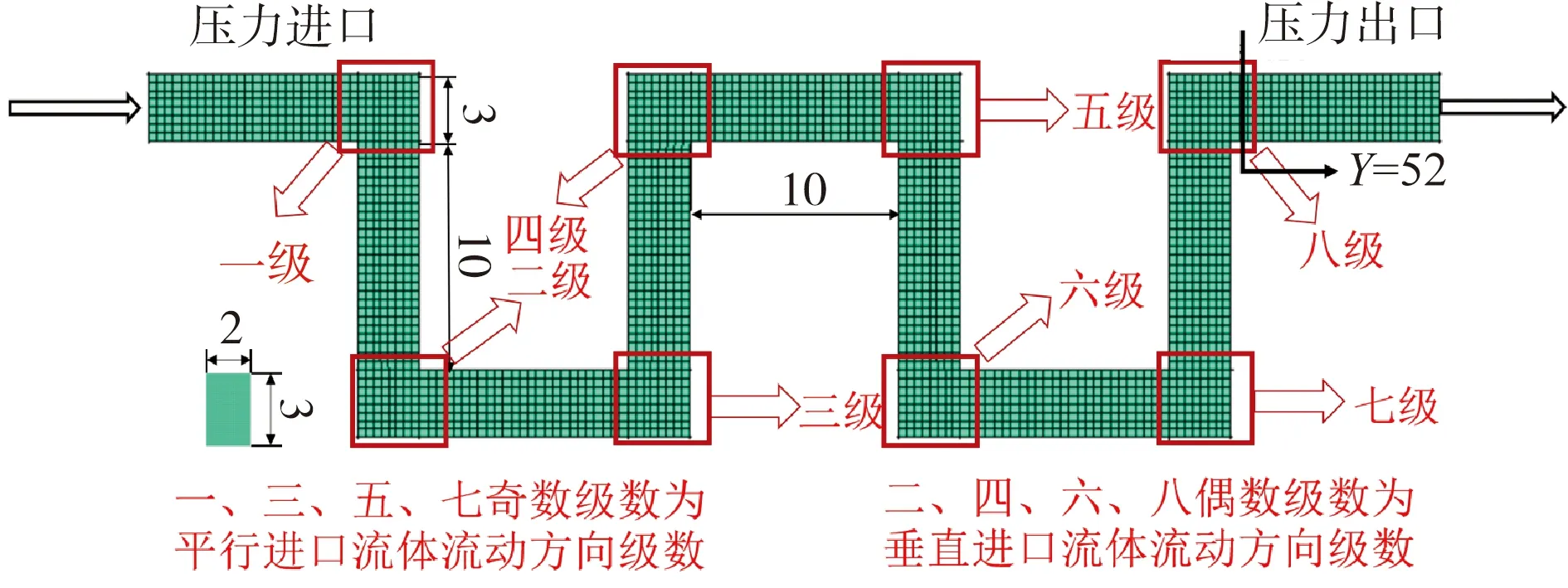
图2 八级流道网格模型Fig.2 Eight stage channel mesh model
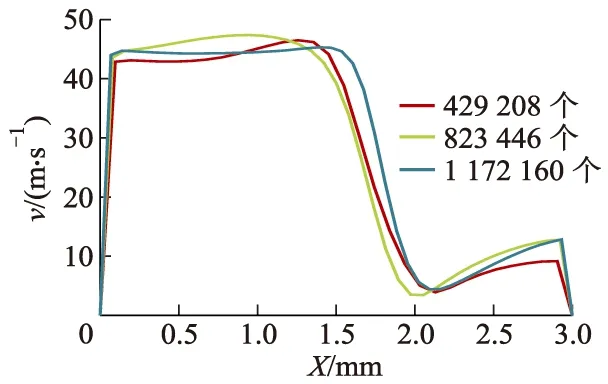
图3 网格无关性验证Fig.3 Grid independence verification
1.2 数值模型的选择
文中采用的Mixture模型被广泛用于模拟不同速度的多相流情况,计算收敛性好且效率较高,且该模型同时忽略气相与液相的可压缩性、温度的影响和各相间的相对速度,相对于VOF模型更加适合空化数值模拟.选择计算精度较高的Realizablek-ε湍流模型,因为它在其他k-ε湍流模型的基础上增加了一个更为合理的湍流黏度公式和一个新的能量消散率传输方程[9].
Schnerr-Sauer空化模型中不含经验常数,能够准确地计算蒸发过程中空泡的生成、发展、脱落和溃灭,其空化模型蒸汽输运方程计算式为
(1)
当p (2) 当p>pv时, (3) RB={3αV/[4πn0(1-αV)]}1/3, (4) 上述式中:uj为速度分量,m/s;ρm,ρl,ρg分别为混合相、液相和气相密度,kg/m3;αV为气相体积分数;Re为蒸汽生产率;Rc为蒸汽凝结率;RB为空泡半径,取1.0×10-6m;p,pv分别为流场压力和汽化压力,Pa. 数值模拟的流程如图4所示,其保证了获得的临界进口压力自身并未空化,当进口压力增加0.1 MPa后由于流道内的局部压力低于饱和蒸气压pe=3 540 Pa便发生了空化.最终,获得了二级、四级、六级、八级流道在出口压力p1分别为0.1,0.2,0.3,0.4,0.5,0.6,0.7和0.8 MPa下的临界空化进口压力p2. 图4 计算临界空化压力流程图Fig.4 Flow chart of calculating critical cavitation inlet pressure 将文中所使用空化模型对过流面积骤减易在收缩段产生局部低压区导致空化的收缩喷嘴进行数值计算,并与ROOSEN等[10]对收缩喷嘴内流场的空化现象试验结果进行对比,验证空化模型的准确性.计算过程中采用与试验过程相同的边界条件,采用Realizablek-ε湍流模型、Schneer-Sauer空化模型和压力与速度耦合的PISO算法,近壁面采用标准壁面函数法进行处理,壁面无相对滑移速度.计算结果与利用 PIV技术观测喷嘴收缩段(长、宽分别为1.0 mm×0.4 mm二维模型)在不同出口压力下空化特征进行对比如图5所示. 从图5可以看出,喷嘴在收缩段的入口近壁面处开始空化,不同出口压力对应的空化长度不同.其中pl=2.1 MPa时,试验空化带的长、宽为0.22,0.08 mm,数值模拟结果空化带长、宽为0.24,0.09 mm,气相最大体积分数为0.954;当pl=1.1 MPa时,试验和模拟结果的空化带长度充满了整个喷嘴收缩段近壁面,试验空化带宽为0.14 mm,数值模拟结果空化带宽度为0.15 mm,气相最大体积分数为0.968.根据对比结果可知,采用文中构建的空化模型计算的数值结果与试验结果基本一致,验证了空化模型的准确性. 图5 试验与数值模拟对比图Fig.5 Comparison between experiment and numerical simulation 图6为不同工况下八级流道的压力云图和截面静压值.从图中可以看出,无论空化还是未空化工况,其降压特性曲线整体呈现阶梯状下降趋势.除进口第一级对应的截面1-2的降压值和出口第八级对应截面8-9的降压值相对较大外,与流动方向垂直的级数二、四、六级对应的截面2-3,4-5,6-7降压值较大,而与流动方向平行级数三、五、七级对应的截面3-4,5-6,7-8压力只显示出微量上升趋势.如图7,8所示的数据表明,不同工况下空化、未空化降压值都表现出相同的规律. 图6 不同工况下八级流道的压力云图和截面静压值Fig.6 Pressure nephogram and section static pressure value of eight stage channel under different working conditions 图7为空化处Y=52~61 mm截面中心线上的压力值.Y=52 mm截面中心线压力值最高,在X方向无明显的压力梯度;Y=53 mm中心线X方向压力梯度最大,在X=2.0~3.0 mm处压力低于饱和蒸气压3 540 Pa,发生空化;Y=54~56 mm截面整体压力值逐渐降到最低,空化扩大为X=1.8~3.0 mm;Y=57~61 mm压力值整体逐渐上升最终达到出口压力值. 图7 Y=52~61 mm中心线压力值Fig.7 Y=52-61 mm center line pressure valve 根据压力低于饱和蒸气压的区域判断空化产生大概位于Y=52~56 mm,X=1.8~3.0 mm区域. 图8为不同工况下八级流道的速度云图和截面速度值.根据伯努利方程可知,流体经过转折流道压力下降,速度理应不断升高,但除截面1-2间有明显上升外其他截面速度却基本保持不变.流体与壁面发生冲撞后,静压能转化为速度动能,流体速度的方向也被流道改变,发生分离产生旋涡导致了能量耗散,矢量图显示截面1-2涡流耗散的动能相对其他截面间较少.而其余平行流道级数截面并无降压且无旋涡产生,这也验证了上述平行流道无降压的结论. 图8 不同工况下八级流道的速度云图和截面速度值Fig.8 Velocity contour plots and section velocity value of eight stage channel under different working conditions 诱导旋涡产生的原因是流体撞击壁面后速度分布不均,分析空化处速度梯度如图9所示.Y=54~56 mm速度梯度最大,X=0~1.5 mm速度值最大为47 m/s,X=1.5~2.2 mm速度持续下降接近于0,X=2.2~3.0 mm速度增加至12 m/s.可以得知Y=52~56 mm,X=1.5~3.0 mm处产生旋涡,速度最低点为旋涡中心.而低压低速的旋涡位置也易发生空化. 图9 Y=52~61 mm中心线速度梯度Fig.9 Y=52-61 mm center line velocity gradient 图10为空化水相分率图,由图可知空化只产生在Y=52~56 mm,X=1.5~3.0 mm处,流道其他位置并未有空化产生,其原因是流体介质经过迷宫流道的多级降压后,在出口流道旋涡处形成低压区,低于饱和蒸气压,诱导空化的产生,空化位置与压力低于饱和蒸气压和产生旋涡的位置一致,所以空化位置一般产生在低于饱和蒸气压的旋涡处,不同级数不同工况下的空化位置大致相同.截面云图显示Y=52 mm近壁面处有少量液体闪蒸出水蒸气;Y=53 mm处空化程度和范围最大且水蒸气体积分数到达最大值为0.798;Y=54~56 mm空化程度逐渐减少,到达Y=56 mm处空化即将消失. 图10 空化水相分率图Fig.10 Cavitation water phase fraction diagram 根据文献定义空化指数σv表征迷宫流道发生空化的难易程度[11],计算式为 (5) 选择不同级数在出口压力分别为0.1~0.8 MPa下的临界空化工况进行计算空化指数σv,发现相同级数临界空化指数非常接近,误差在0.2%~0.4%,分别求出二级、四级、六级、八级下流道的临界空化指数为0.746 8,0.778 4,0.827 1,0.854 2.临界空化指数随级数的增大而增加.根据式(5)可知,p1≫pe,空化指数σv小于1,且σv越大,所需要的进口压力p2的值越大,越难发生空化.因此,流道级数越多,越难发生空化现象. 根据现有数据整理筛选得到二级、四级、六级、八级的临界空化压力规律,如图11所示,图中pd为临界空化出口压差. 图11 递增出口压力和递增级数下临界空化压差趋势线图Fig.11 Trend chart of critical cavitation pressure difference with increasing outlet pressure and increasing stages 从图11a可以看出,伴随出口压力的逐渐递增,临界空化压差呈现线性函数递增规律,其拟合趋势线方程能够准确预估未测出口压力下的临界空化压差,推断出临界进口压力.相同出口压力情况下,伴随级数递增临界空化压差显然呈现递增趋势,这与级数越多,所能承受的临界空化压差越大相契合. 从图11b可以看出,伴随流道级数偶数递增,临界空化压差呈现指数函数增加趋势,可根据拟合趋势线方程预测未测级数下的临界空化压差.相同级数情况下,伴随出口压力的递增,其相邻不同工况出口压力下的临界压差逐渐减少,结果显示,当级数选定的时候,出口压力到达0.4 MPa后,再增加出口压力去获得抗空化能力的措施收益相对较小,选用合适的流道级数去适应其运行工况才是有效的措施. 1) 除进出口级数都会产生较大的降压外,与流体流动方向垂直的级数降压值较大,而与流体流动方向平行的级数降压值基本保持不变.除进口级数速度保持一致上升外其他流道级数的主流速度基本保持不变,原因是在降压较大的级数内流体碰撞壁面静压能转化为动能后产生了旋涡的能量耗散,以保持速度的稳定,未产生降压的级数则没有旋涡产生. 2) 在出口近壁面处,当速度梯度较大的旋涡中心低压区的压力低于饱和蒸气压时,便会诱导空化产生.且流道级数越多,临界空化指数就越大,也就越难发生空化现象. 3) 相同级数情况下,伴随出口压力逐渐递增,临界空化压差呈现线性函数增长.相同出口压力情况下,伴随级数递增,临界空化压差呈现指数函数增长.可根据趋势线方程预估直流式流道在不同出口压力和不同级数下的临界空化进口压力,从根源上避免空化.2 模拟过程及空化模型验证
2.1 数值模拟过程
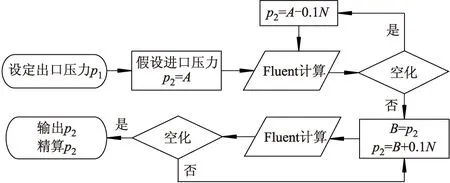
2.2 空化模型验证
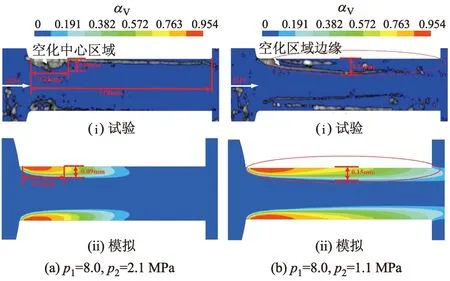
3 数值结果与分析
3.1 降压特性分析
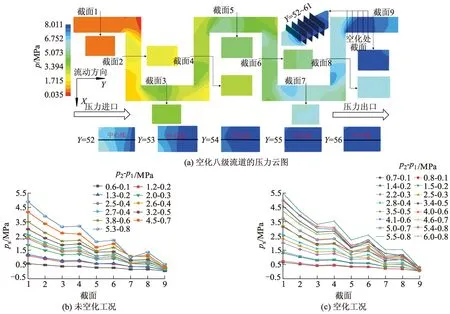
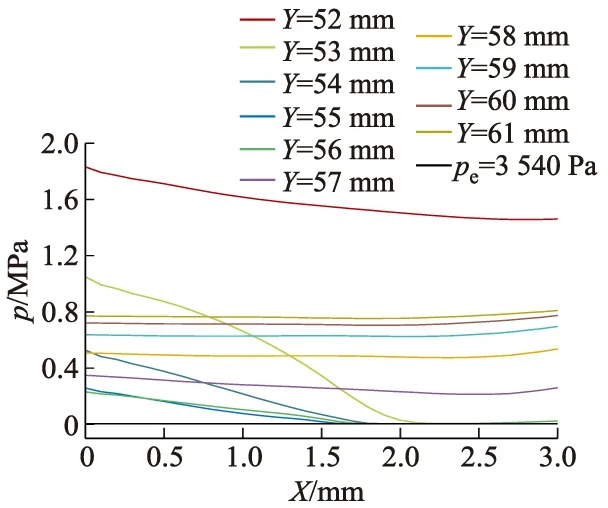
3.2 速度特性分析
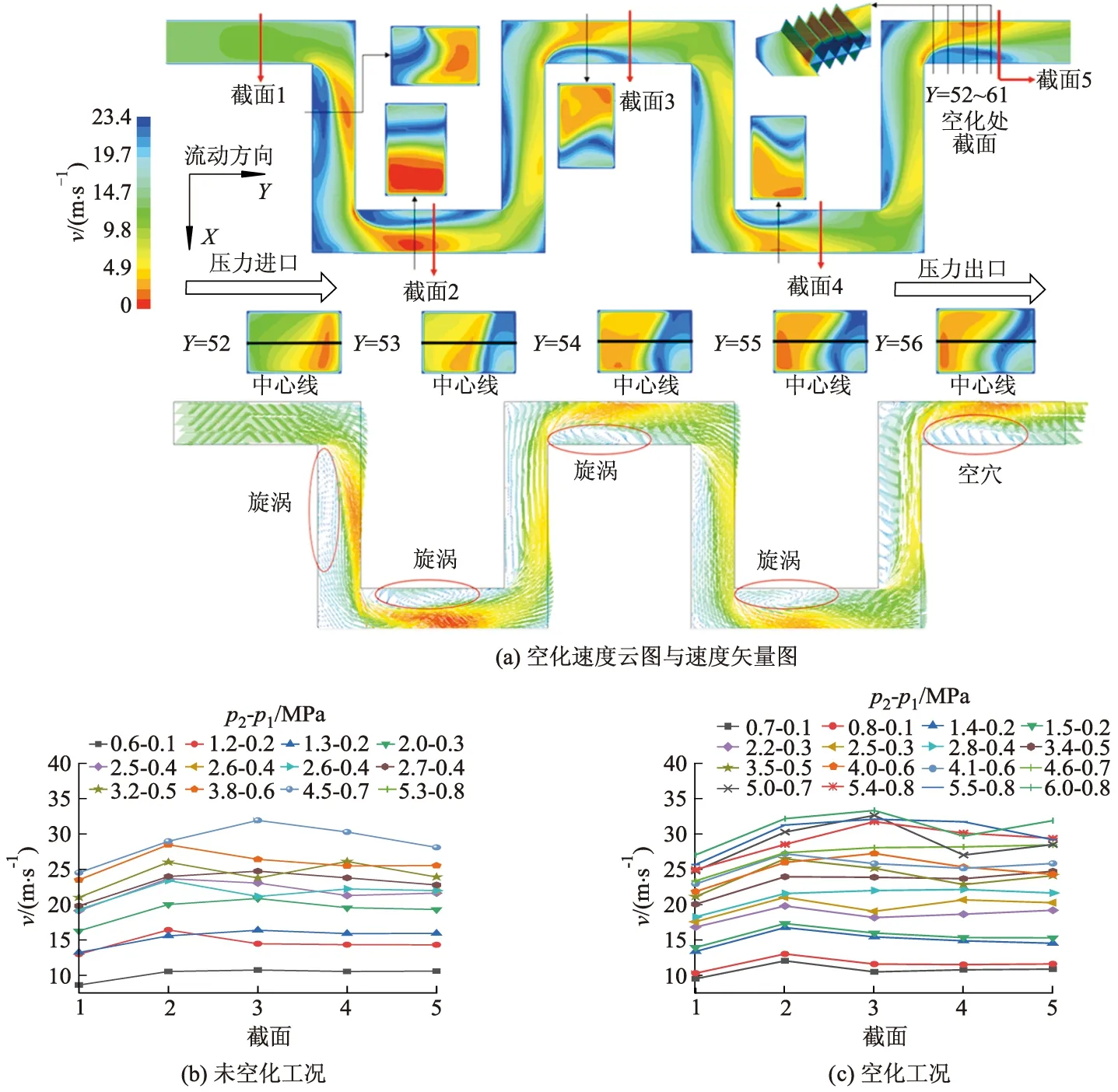
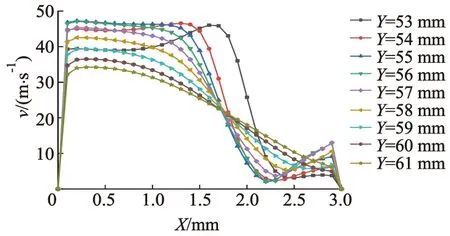
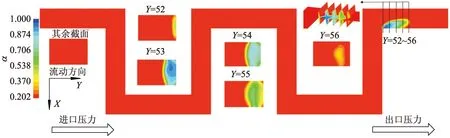
3.3 空化特性分析
3.4 临界空化指数与压力分析
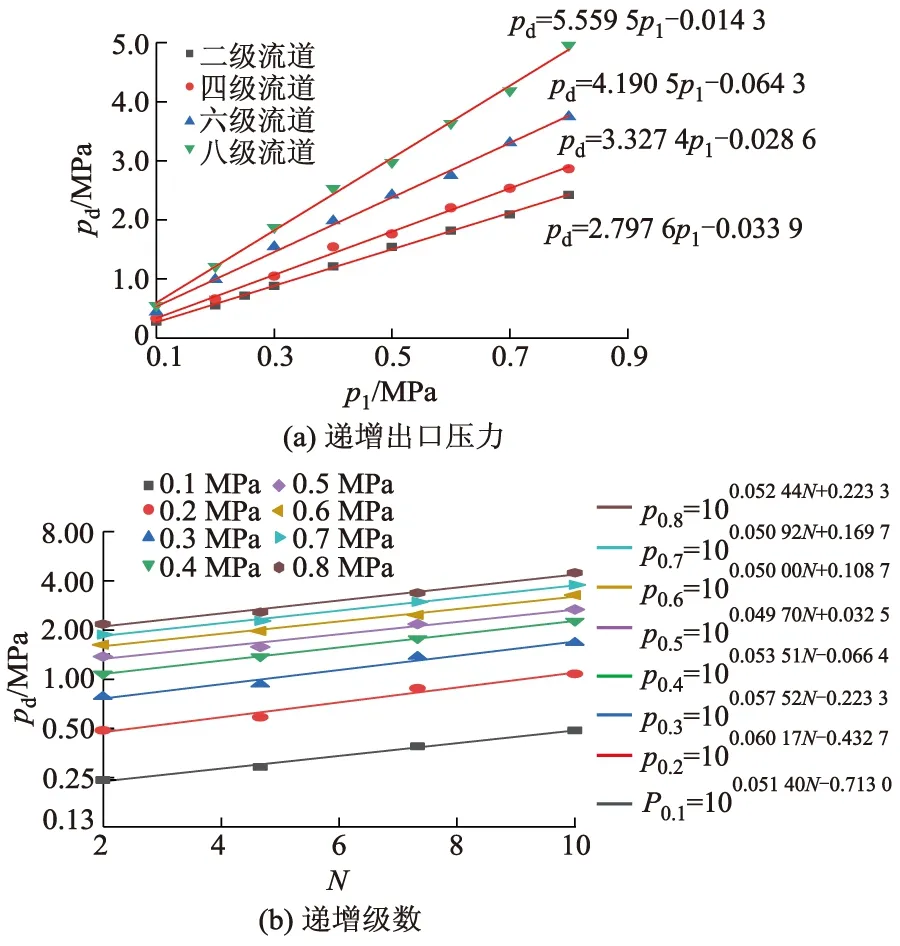
4 结 论
