山区35kV架空线路雷击特性仿真分析

张文锋 李志伟 张国建 林 敢

山区35kV架空线路雷击特性仿真分析

张文锋1李志伟1张国建1林 敢2, 3

（1. 云南电网有限责任公司大理供电局，云南 大理 671000；2. 湖北省输电线路工程技术研究中心（三峡大学），湖北 宜昌 443002；3. 三峡大学电气与新能源学院，湖北 宜昌 443002）

本文分析大理山区架空线路典型地形特点，基于雷电定位系统采集的线路雷电活动数据，计算山脊、山坡、山谷及平原等典型地形条件下线路的耐雷水平及直击雷和感应雷跳闸率，获得山区地形下架空线路雷击跳闸率的变化规律。结果表明：不同地形条件下架空线路的雷击跳闸率差异较大，位于山脊的线路直击雷跳闸率较大，其随两侧的坡度减小而变小；而位于山谷的线路，感应雷跳闸率较大，其随着坡度的增加而增大；山区线路的雷击跳闸率相比平原地区高64%左右。

架空线路；山区；地形；雷击跳闸率；感应雷过电压

0 引言

35kV架空线路作为中压输配电线路中的主体，具有覆盖区域广、网架结构复杂等特点，我国相关规程仅对35kV线路进线段作了架设避雷线的要求[1]，导致其整体防雷能力较差，容易受到雷电侵害。据统计，架空线路的雷害事故大概占整个电力系统全部雷害事故的70%～80%[2-3]。特别是位于山区的架空线路，由于山区地形地貌及气候环境的影响，土壤电阻率偏高，雷电活动更为活跃，雷击导致的线路跳闸风险更高[4]。因此，研究山区地形对架空线路雷击特性的影响具有重要的实际意义。

目前，针对山区地形对输电线路屏蔽特性的影响开展了较多研究。文献[5]分析不同地形对输电线路雷电防御性能的影响，发现地形条件使线路在高度增加或暴露区域扩大时遭受雷击的概率更高。文献[6]基于电气几何法提出输电线路错层塔上坡位上相导线雷击绕击率计算方法，计算结果表明，错层塔上坡位上相面临较大雷击风险。文献[7]分析不同地面倾斜角度下杆塔高度、风速和保护角等对±800kV线路雷电屏蔽性能的影响。文献[8]提出一种适用于山区地形的输电线路雷击概率计算模型，分析山顶地形对雷电先导的吸引作用。文献[9]分析微地形与雷电活动、雷击故障的相关性。文献[10]分析线路走廊地形条件对其雷害风险的影响，指出随着线路走廊所在坡面的角度变大，线路发生雷击故障的概率会上升。可见，地形对线路的雷击特性影响较大，但现有研究主要以输电线路为主，针对山区不同地形条件下架空线路的雷击特性尚缺乏系统研究。

本文对大理山区线路的典型地形进行分析，建立考虑地形的改进电气几何模型，并利用ATP- EMTP搭建山区35kV架空线路雷击过电压计算模型，计算山脊、山坡、山谷及平原等典型地形下线路的直击雷和感应雷跳闸率，获得山区地形下架空线路雷击跳闸率的变化规律，为山区架空线路的雷电防护提供参考。

1 大理山区架空线路雷击数据分析

1.1 大理35kV架空线路运行情况统计

数据资料显示，大理35kV架空线路2019年因雷击引起的跳闸事故为47次，占总跳闸数的92%，其中重合闸成功28次，成功率为59%；2020年由雷击引起的跳闸次数为27次，占总跳闸次数的90%，雷击跳闸次数同比下降42.55%，其中重合闸成功次数为17次，成功率为63%，同比上升4%，故障统计如图1所示。

图1 大理35kV架空线路雷击故障统计

对比分析可知，2020年大理35kV架空线路运行状况有所改善，但雷击故障仍是影响线路正常运行的最主要因素，且以感应雷引起的跳闸为主。

1.2 大理山区架空线路走廊地形分析

大理地区架空线路走廊地形主要分为平地与山区两种，其中山区又包含山地与丘陵[11]，由于不同的走廊地形对线路的影响较大，需要对山区地形下的架空线路走廊进行更为细致的区分。以大理山区35kV漾富线为例，该线路共有杆塔105基，全长30.646km，走廊地形包含山坡、山脊、山谷、平原等，线路整体走向如图2所示。

考虑到山区地形的差异主要因坡面之间的组合，以及导线与山坡所在平面的关系不同而产生，以下列出常见的架空线路沿线地形：①导线水平方向平行于坡面，其根据杆塔位置的不同又有三种不同情况，即杆塔位于山顶、山坡和山谷；②导线垂直方向平行于坡面，根据坡面的不同组合有爬坡与跨谷两种情况。具体不同地形如图3所示。

对于架空线路来说，地形地貌的影响主要包括：①影响线路雷电屏蔽性能，从而直接影响雷击跳闸率；②山区土壤电阻率与平原差异较大，山区土壤一般为岩石、碎石或片石等地质，造成土壤电阻率偏高；③山区雷电活动强度相比平原更大，导致雷暴日和地闪密度等参数高于平原地区。因此，有必要对山区架空线路的雷击特性开展相关研究。

2 考虑地形的架空线路雷击过电压计算模型

2.1 考虑地形的改进电气几何模型

电气几何模型如图4所示。传统的经典电气几何模型没有考虑地面倾角对击距的影响，而对山区架空线路来说，地形因素的影响十分显著，下面对不带避雷线的电气几何模型进行分析[12]。

如图4（a）所示：在经典电气几何模型上加入地面倾角，假设线路平行于山坡坡面架设，杆塔垂直于水平面，导线位于点，高为；s和g分别为雷电对导线和大地的击距，且g=s，为击距系数，本文取0.9；为以为圆心，s为半径的圆弧，平行于坡面，与坡面的垂直高度为g。考虑雷电流的大小对击距的影响，引雷宽度需分以下两种情况讨论：

1）当点的水平高度小于或等于点，如图4（a）中点时，得到引雷宽度=s。

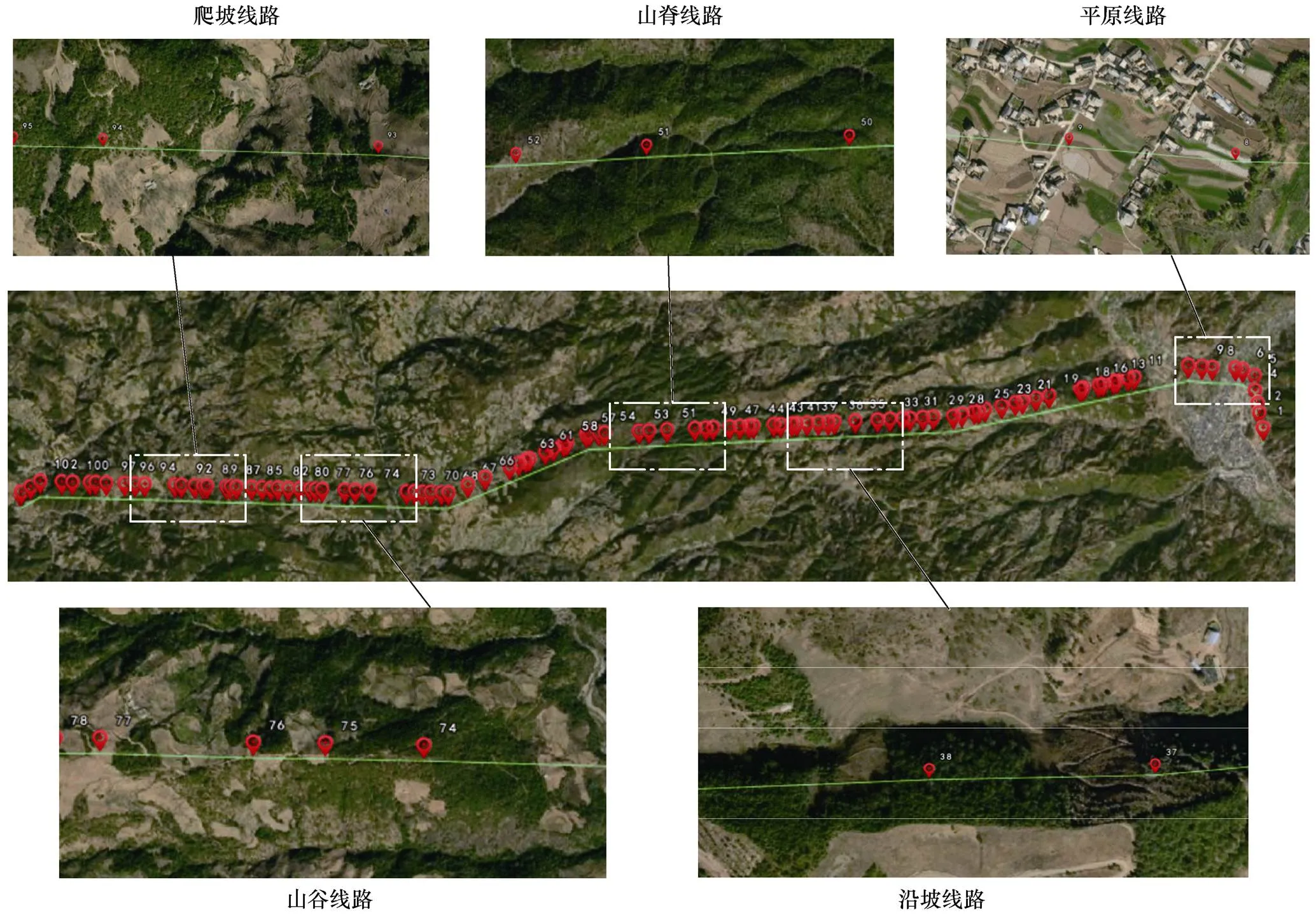
图2 大理35kV漾富线整体走向

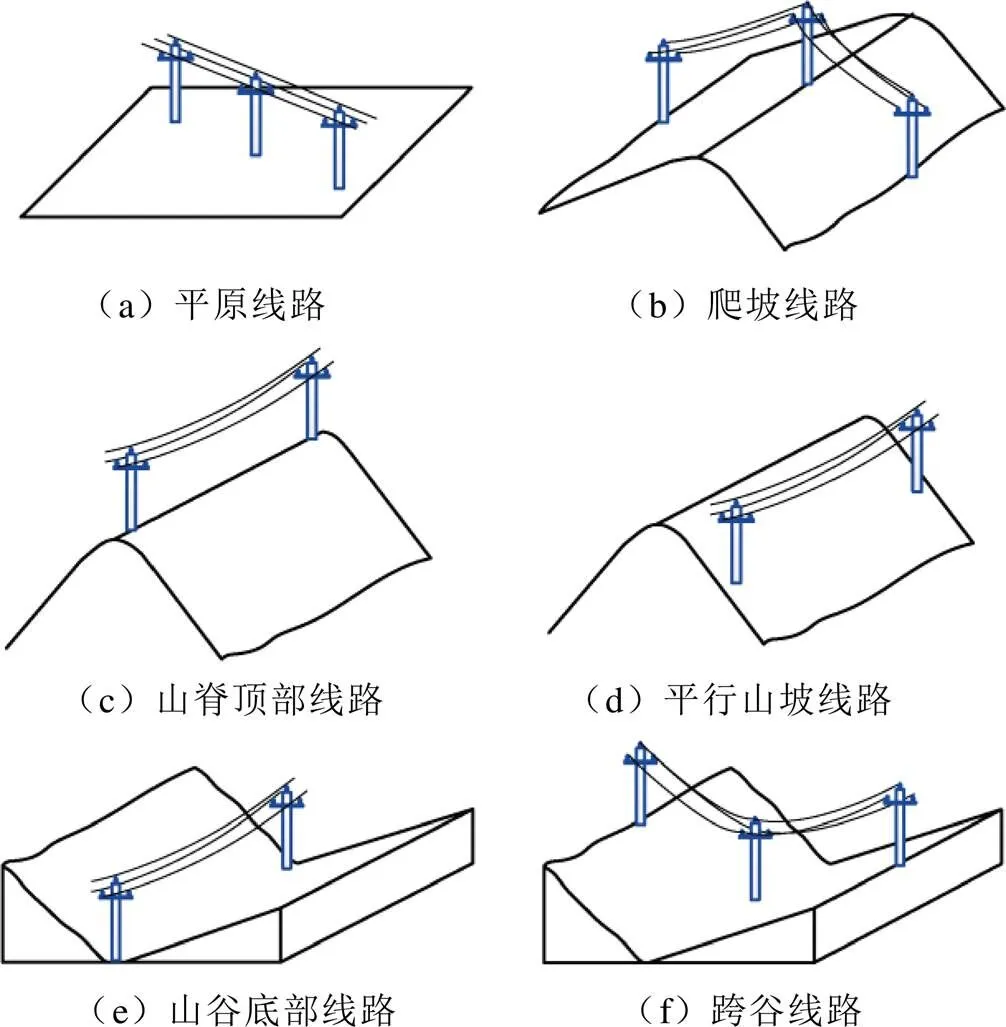
图3 大理山区架空线路典型地形

2）当点的水平高度高于点时，如图4（a）中点，坐标为（,），引雷距离为s在水平面上的投影，此时引雷宽度=。

对于装设避雷线的线路，需额外考虑避雷线与大地之间倾角的关系，如图4（b）所示：为线路横担宽度，为避雷线保护角，1、2分别为、与水平面之间的角度；为避雷线保护弧，为绕击弧，其在水平面上的投影与分别为反击与绕击引雷宽度，对于超过之外的部分，即感应雷引雷宽度。与未安装避雷线的情况类似，雷电流幅值将影响大地与线路的雷电击距，因此对于线路的引雷宽度需要分以下四种情况讨论：

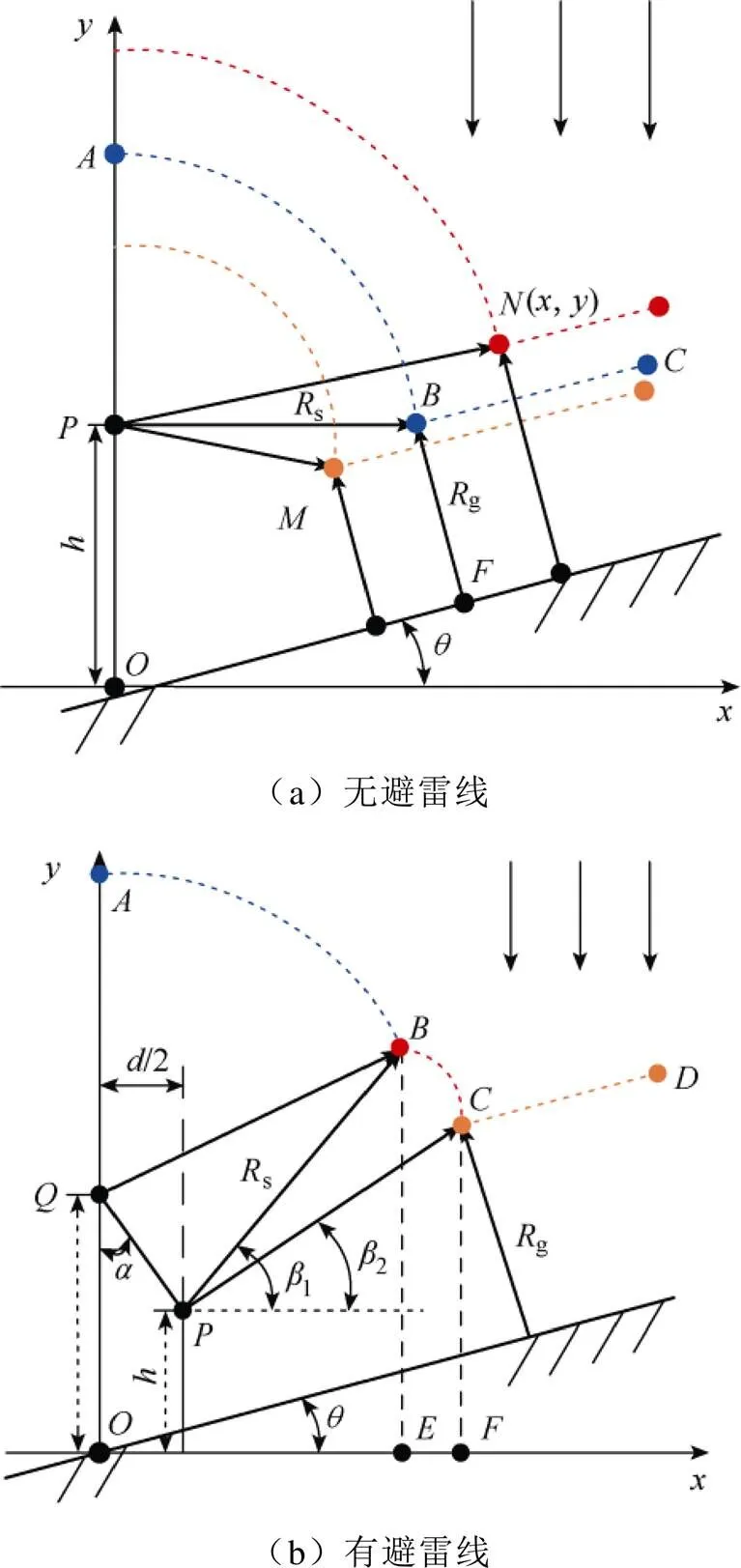
图4 电气几何模型

1）当雷电流足够小时，不考虑大地对线路的保护，反击引雷宽度=s，绕击引雷宽度=/2。

2）当雷电流进一步上升，至点与点处于同一水平线时，反击引雷宽度为=scos1+/2，绕击引雷宽度为=s(1-cos1)。

3）当雷电流进一步上升，至点高于点但低于B点时，导线未被避雷线完全保护，其反击引雷宽度为=scos1+/2，绕击引雷宽度为=s(cos2-cos1)。

4）当雷电流进一步上升，至点高于点时，导线被避雷线完全保护，理论上不会发生绕击，此时的引雷宽度=s。

上述表达式中的1与2的计算公式分别为

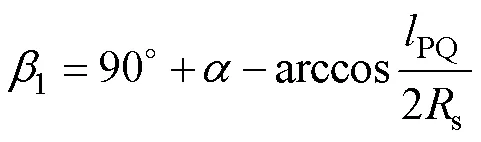
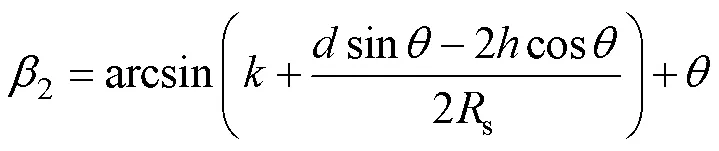
式中：PQ为避雷线到导线距离；为击距系数，与前文相同。

2.2 35kV架空线路雷击过电压计算模型

以图2中的35kV漾富线为原型，建立雷击过电压计算模型如图5所示，取档距平均值为300m，导线型号为LGJ—150/20钢芯铝绞线，弧垂1.5m，线路采用Bergeron模型模拟[13-15]。雷电流波形参数设置为2.6/50ms，模型采用Heilder模型进行模拟，该模型与实际雷电流波形较为吻合，相较于双指数模型其参数设置更加简便[16]。杆塔为“上”字形，由多段波阻抗组成，波阻抗值取125W，接地电阻取固定值10W。绝缘子为FXBW—35/70复合绝缘子，其负极性冲击放电电压50%=250kV，计算过程采用基于定义法的Models自定义元件进行模拟。

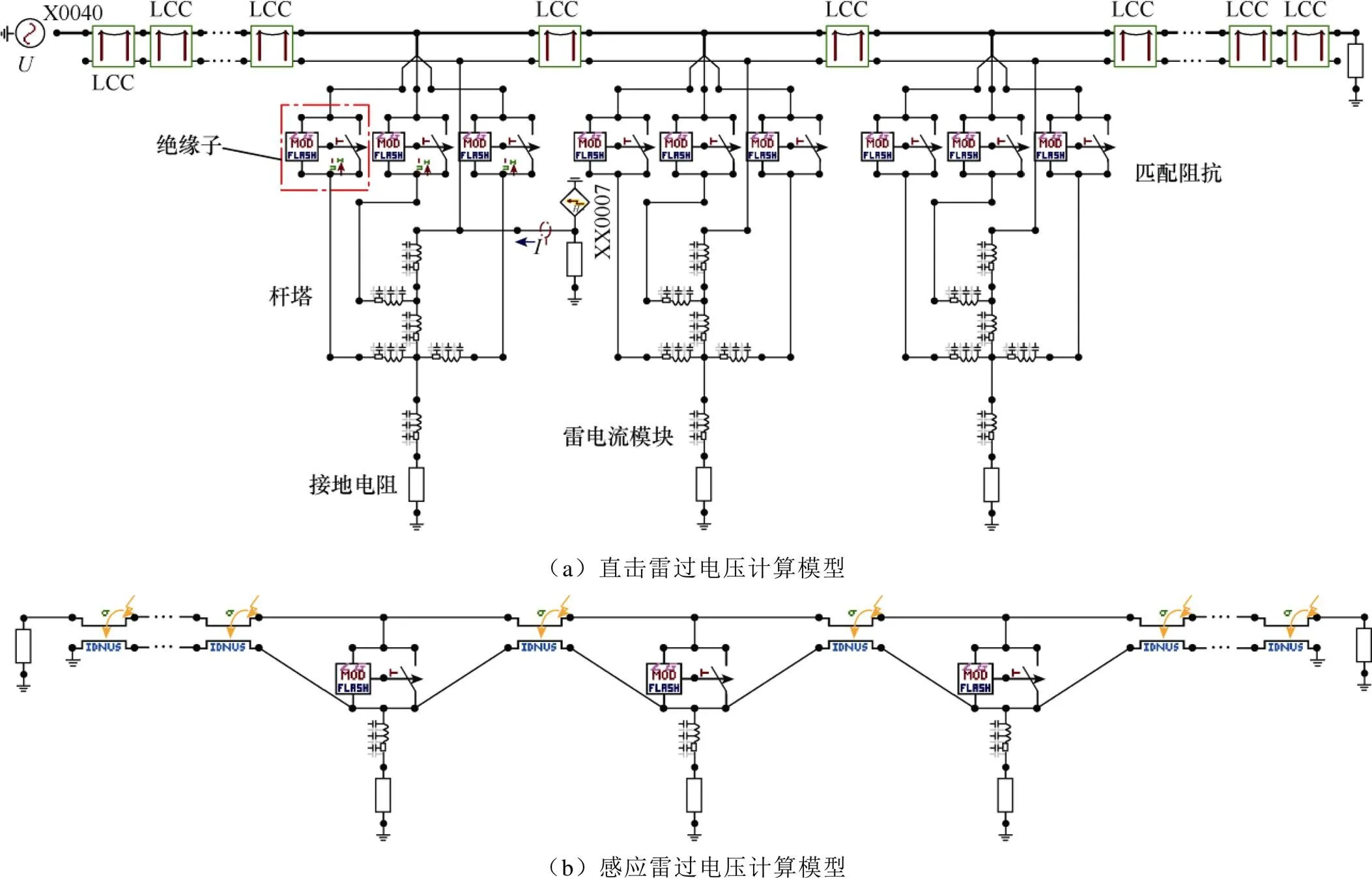
图5 雷击过电压计算模型

本文的感应雷过电压计算，通过在ATP软件中调用Models语言编程的MOD感应过电压子模块来实现[17]，该方法基于如下假设[18-19]：

1）感应电压由雷击主放电过程中的磁效应与静电效应组成。

2）雷电回击通道与大地垂直，回击速度保持不变，先导发展过程中电荷均匀分布。

3）大地为均匀土壤，电导率和介电常数为常数；架空线路认为是无损的，有损大地主要影响空间电场的水平分量。

4）电磁场与线路耦合过程采用Agrawal场线耦合模型[20]。

建立的35kV架空线路直击雷和感应雷过电压计算模型分别如图5（a）和图5（b）所示，该计算模型可对雷电流、雷击位置、杆塔等参数进行修改，通用性较强。

3 考虑地形的雷击跳闸率计算

3.1 计算方法

考虑地形的雷击跳闸率计算流程如图6所示，具体如下：

图6 考虑地形的雷击跳闸率计算流程

1）确定35kV架空线路的线路参数、杆塔类型和绝缘强度等，采用电磁暂态仿真软件ATP-EMTP建立直击雷和感应雷过电压仿真模型。

2）改变雷电流幅值，通过观察绝缘子两端的电压波形，得到耐雷水平。

3）根据上述改进电气几何模型，获得山区地形下线路的引雷宽度。

4）计算直击雷跳闸率。

假设雷电流峰值最大不超过200kA，线路反击跳闸率TRa和直击导线跳闸率TRb的计算公式为

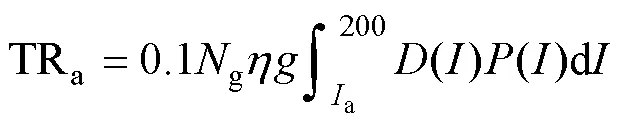
式中：g为地闪密度（次/(km2·a)）；为建弧率；为击杆率；线路引雷宽度()=1(,1)+2(,2)+，D1、D2为两侧导线的引雷宽度（m），1、2为两侧地面的倾角，为两侧导线的相间距离（m）；()为雷电流幅值大于的概率；a为雷击杆塔（反击）耐雷水平（kA）；b为雷击导线（绕击）耐雷水平（kA）。

将雷电流幅值的取值范围设为0～200kA，以1kA为间隔，分为200个区间，第个区间为[,+1]；将上述直击雷跳闸率积分计算公式（3）和式（4）进行离散求解，最终获得直击雷跳闸率的表达式为

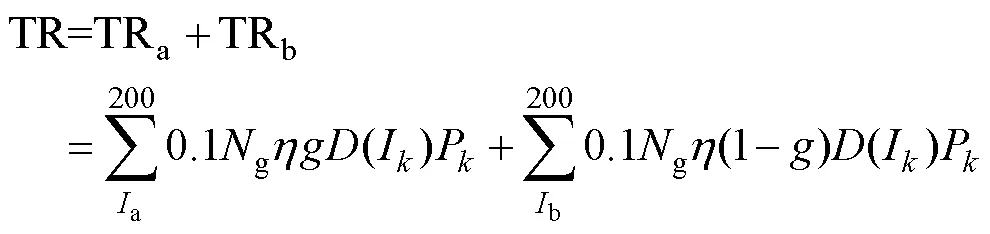
根据对云南高海拔地区雷电活动情况的分析[21]，雷电流幅值大于的概率如式（6）所示，则第个区间雷电流出现的概率计算式如式（7）所示。

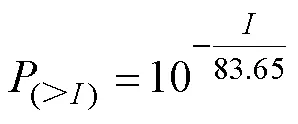
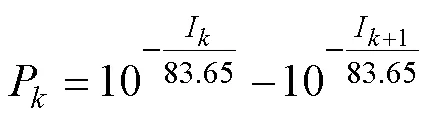
5）计算感应雷跳闸率。

与直击雷跳闸率的计算不同，感应雷跳闸率计算中，首先需确定感应雷的引雷区域，感应雷电气几何模型如图7所示。

图7 感应雷电气几何模型

架空线路的感应雷跳闸率计算公式为

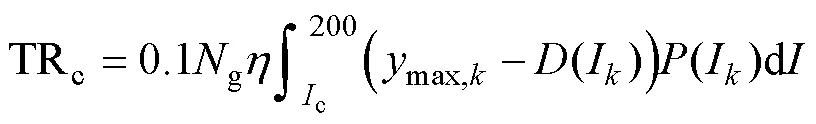
式中：ymax,k为感应雷电流幅值为Ik时的最大临界闪络距离，受雷电流幅值及地面倾角影响（m）；D(Ik)为雷击大地的最大临界距离（直击雷引雷范围）（m）；Ic为感应雷耐雷水平（引起线路发生感应雷跳闸的最小雷电流幅值）（kA）。当雷电流幅值高于Ic且ymax,k大于D(Ik)时，才存在发生感应雷跳闸的可能。ymax,k计算流程如图8所示。

由于线路的感应雷耐雷水平与雷击点到线路距离呈正相关，随着雷击点距离变远，线路上的感应过电压会变小，计算得到的线路的耐雷水平相对上升，反之亦然。因此对于某一确定雷电流，假设其峰值为，首先给定初值0（雷击点距线路垂直距离为0，其取值尽量小，此时对应的耐雷水平c也较小），利用建立的仿真模型计算耐雷水平c，若耐雷水平c＜，则令0=0+D，重复计算，直至c与基本一致时，得到的雷击距离即为平原地区的最大临界闪络距离max()，将计算值拟合成函数，可得到最大临界闪络距离max随雷电流幅值的变化规律。

根据电气几何模型可知，不同雷电流下的引雷范围不同，传统雷击跳闸率计算时，认为不同雷电流的引雷范围相同，使计算结果产生误差，因此，对[0, 200kA]的雷电流以1kA为步长划分为200个区间，并利用图8所示方法确定对应的max,k。

对上述感应雷跳闸率计算公式（8）进行离散求解，最终可获得感应雷跳闸率的离散表达式为

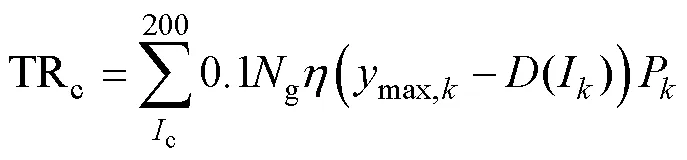
3.2 直击雷计算结果分析

根据雷电定位系统统计数据信息，得到漾富线近年的平均地闪密度为3.2次/(km2·a)。参照IEEE标准选取=0.5[22]；两侧导线的相间距离为5m；绝缘子放电距离取0.45m，根据计算建弧率=0.56。杆塔的工频接地电阻一般取10～30W，考虑到山区土壤电阻率往往较大，因此，仿真中山区地形的土壤电阻率取1 000W·m，杆塔接地电阻取25W；平原地区的土壤电阻率取100W·m，接地电阻取10W。

计算得到平原和山区架空线路的直击雷耐雷水平见表1。由于山区的土壤电阻率及接地电阻比平原地区高，因此，其直击雷耐雷水平更低。

表1 直击雷耐雷水平 单位：kA

根据上述计算方法，在如图9所示不同山区地形下，分别计算线路的直击雷跳闸率，具体如下。

图9 不同山区地形

1）平原及山区平地线路1=2=0°

计算平原与山区平地线路的直击雷跳闸率，结果见表2。

对比表2中数据可知，在相同地闪密度条件与地形倾角下，山区线路有、无避雷线的直击雷跳闸率分别比平原线路高出197.87%、48.48%，可见，高土壤电阻率与接地电阻是使线路雷击风险上升的重要因素之一。

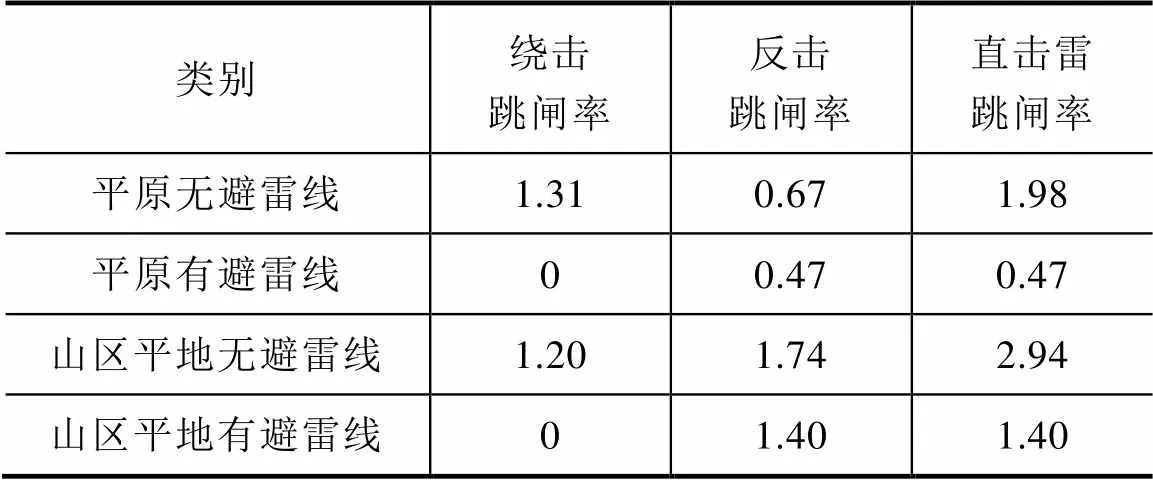
表2 地形倾角为0°时直击雷跳闸率计算结果 单位：次/(100km·a)

2）山脊线路1=2∈[-30°,-5°]

根据考虑地形的电气几何模型，当线路位于山脊处时，线路的暴露面积相比平原更大，即线路的引雷宽度将变大。图10为山路线路直击雷跳闸率随线路两侧坡度的变化规律。

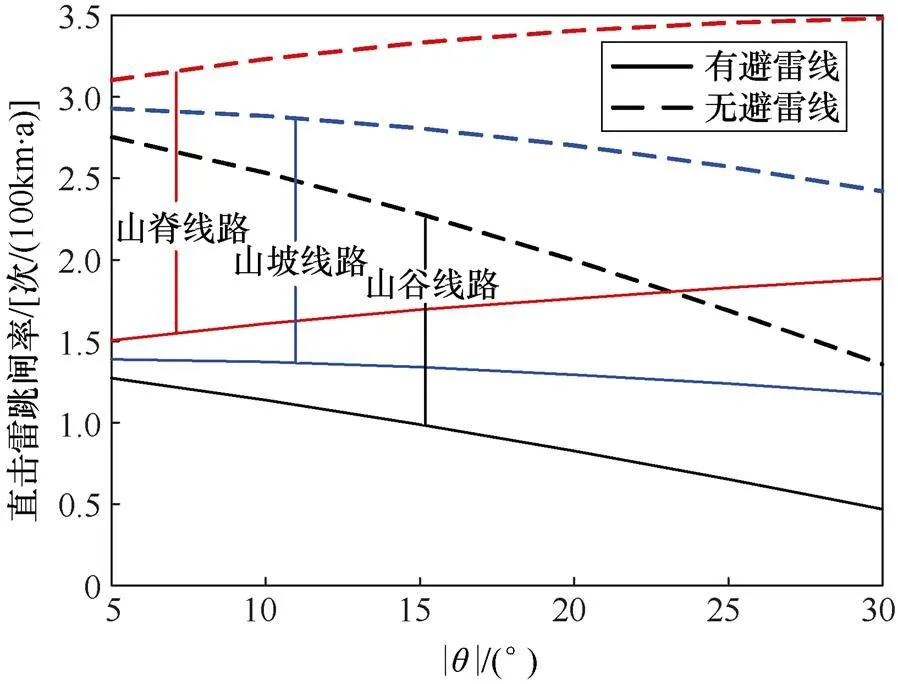
图10 山区线路直击雷跳闸率随线路两侧坡度的变化

由图10可知，山脊线路直击雷跳闸率随两侧坡度的增大而增大。无避雷线的情况下，两侧的坡度从-5°变为-30°时，山脊线路直击雷跳闸率从3.1次/(100km·a)升至3.48次/(100km·a)；两侧倾角为-30°时，山脊线路直击雷跳闸率相比山区平地线路增大了0.54次/(100km·a)，增幅约为18.37%。有避雷线的情况下，山脊线路直击雷跳闸率从1.5次/(100km·a)升至1.88次/(100km·a)；两侧倾角为-30°时，山脊线路直击雷跳闸率相比山区平地线路增大了0.48次/ (100km·a)，增幅约为34.29%。

3）山坡线路1=-q2∈[5°, 30°]

当线路位于山坡处时，线路的暴露面积受两侧地形的影响。位于上坡侧的线路，由于地面的引雷作用，其引雷宽度变小，而位于下坡侧的线路引雷宽度则变大。

由图10可知，山坡线路的直击雷跳闸率随坡度的增加而逐渐变小。无避雷线的情况下，当坡度从5°变为30°时，山坡线路的直击雷跳闸率从2.93次/ (100km·a)降至2.42次/(100km·a)；两侧坡度为30°时，山坡线路直击雷跳闸率相比山区平地线路减小了0.52次/(100km·a)，降幅约为17.69%。有避雷线的情况下，山坡线路直击雷跳闸率从1.39次/ (100km·a)降至1.18次/(100km·a)；两侧坡度为30°时，山坡线路直击雷跳闸率相比山区平地线路下降了0.22次/(100km·a)，降幅约为15.71%。

4）山谷线路1=2∈[5°, 30°]

当线路位于山谷处时，在地面的引雷作用下，线路暴露距离相比平原更小，使线路的引雷宽度变得更小。

由图10可知，无避雷线的情况下，两侧坡度从5°上升至30°时，山谷线路的直击雷跳闸率从2.75次/(100km·a)下降至1.36次/(100km·a)；两侧坡度为30°时，山谷线路直击雷跳闸率相比山区平地线路降低了1.58次/(100km·a)，下降约53.74%。有避雷线的情况下，山谷线路直击雷跳闸率从1.27次/ (100km·a)降至0.47次/(100km·a)；两侧坡度为30°时，山谷线路直击雷跳闸率相比山区平地线路下降了0.93次/(100km·a)，降幅约为66.43%。

3.3 感应雷计算结果分析

根据3.2节的参数，计算得到无防雷措施平原和山区平地线路的感应雷耐雷水平分别为58kA和48kA，有避雷线的平原、山区平地线路感应雷耐雷水平分别为82kA和69kA。

根据上述计算方法，得到平原、山区平地线路的有无避雷线条件下感应雷跳闸率见表3。

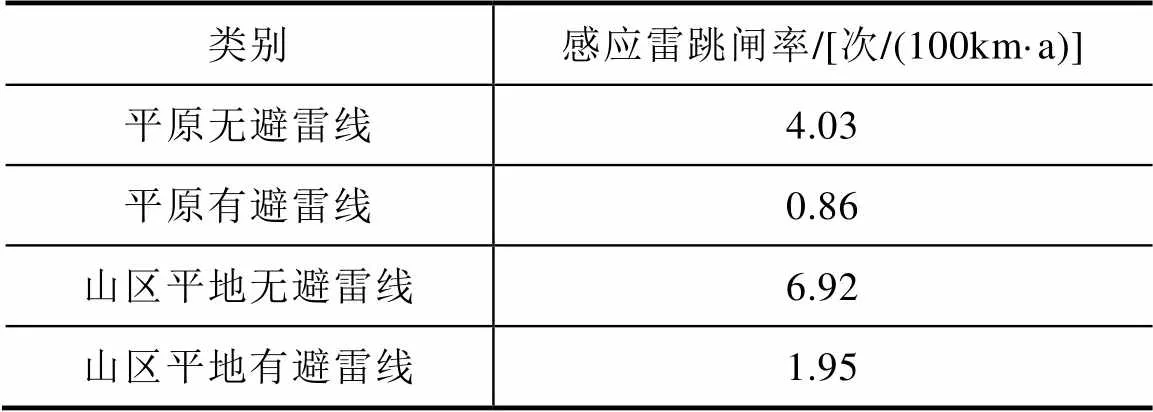
表3 地形倾角为0°时感应雷跳闸率计算结果

由表3可知，虽然杆塔接地电阻对感应雷耐雷水平几乎无影响，但山区比平原地区的大地电导率低，产生的感应过电压较大，导致其感应雷耐雷水平更低，从而跳闸率更高。

1）山脊线路1=2∈[-30°,-5°]

当山区线路发生感应雷时，线路上产生更高的感应过电压，将一定程度地增加最大临界闪络距离，因此，山区的最大临界闪络距离非线性较大且高于平原地区；同时，当线路位于山脊时，直击雷的引雷宽度增加，导致感应雷的雷击区域缩小，最终感应雷的雷击区域大小需综合考虑两者的作用。计算得到山区线路感应雷跳闸率随线路两侧坡度变化的情况如图11所示。

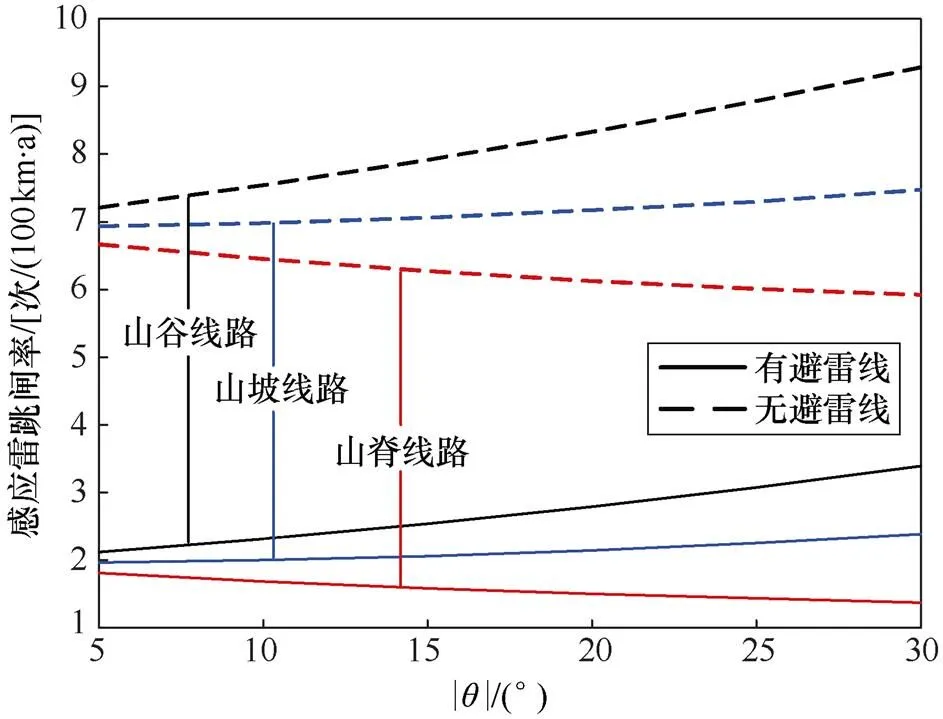
图11 山区线路感应雷跳闸率随线路两侧坡度的变化

由图11可知，山脊线路感应雷跳闸率随两侧坡度的增大而减小。无避雷线的情况下，两侧的倾角由-5°变化至-30°时，山脊线路的感应雷跳闸率由6.67次/(100km·a)下降至5.92次/ (100km·a)；当两侧倾角为-30°时，山脊线路感应雷跳闸率相比山区平地线路减小了1次/(100km·a)，降幅约为14.45%。有避雷线的情况下，山脊线路的感应雷跳闸率由1.81次/(100km·a)下降至1.37次/ (100km·a)；当两侧倾角为-30°时，山脊线路感应雷跳闸率相比山区平地线路减小了0.58次/(100km·a)，降幅约为29.74%。

2）山坡线路1=-q2∈[5°, 30°]

当线路位于山坡处时，线路直击雷的引雷宽度受两侧的地形影响，随倾角的增大，位于上坡侧线路的引雷宽度减小，而位于下坡侧的引雷宽度增大；此时，线路直击雷的引雷宽度变化相对较小，感应雷的雷击区域主要受最大临界闪络距离的影响。

由图11可以看出，无避雷线的情况下，当两侧坡度由5°上升至30°时，山坡线路感应雷跳闸率由6.93次/(100km·a)上升至7.3次/(100km·a)；当两侧坡度为30°时，感应雷跳闸率相比山区平地线路增大了0.38次/(100km·a)，增幅约为5.49%。有避雷线的情况下，山坡线路的感应雷跳闸率由1.97次/ (100km·a)上升至2.38次/(100km·a)；当两侧坡度为30°时，山坡线路感应雷跳闸率相比山区平地线路增大了0.43次/ (100km·a)，增幅约为22.05%。因此，线路位于山坡时，随着坡度的增加，线路感应雷跳闸率逐渐增大。

3）山谷线路1=2∈[5°, 30°]

当线路位于山谷处时，在地面的引雷作用下，线路更易发生感应雷击跳闸事故。

由图11可知，无避雷线的情况下，当线路两侧坡度由5°上升至30°时，山谷线路感应雷跳闸率由7.21次/(100km·a)上升至9.28次/(100km·a)；当两侧坡度为30°时，山谷线路感应雷跳闸率相比山区平地线路增大了2.36次/(100km·a)，增幅约为34.10%。有避雷线的情况下，山谷线路的感应雷跳闸率由2.12次/(100km·a)上升至3.39次/(100km·a)；当两侧坡度为30°时，山谷线路感应雷跳闸率相比山区平地线路增大了1.44次/(100km·a)，增幅约为73.85%。因此，线路位于山谷时，随着坡度的增加，线路感应雷跳闸率逐渐增大。

对比直击雷计算结果可发现，感应雷跳闸率随坡度的变化规律与之完全相反，其主要原因是两者发生雷击跳闸的机理不同。直击雷通过电气几何模型计算线路引雷宽度，当雷击发生在此宽度内时，雷电流直接入侵线路引起跳闸，因此当地形坡度引起引雷宽度发生变化时，直击雷跳闸率也随之改变；而感应雷过电压主要取决于雷电回击通道附近产生的静电场分量，线路所在坡度越大，电场发生的畸变就越明显，从而形成更强的电场，过电压也随之上升，从而更容易引起线路跳闸[20]。

3.4 总雷击跳闸率计算结果分析

根据3.2节直击雷跳闸率和3.3节感应雷跳闸率计算结果，可得到平原与山区平地线路的总雷击跳闸率见表4。

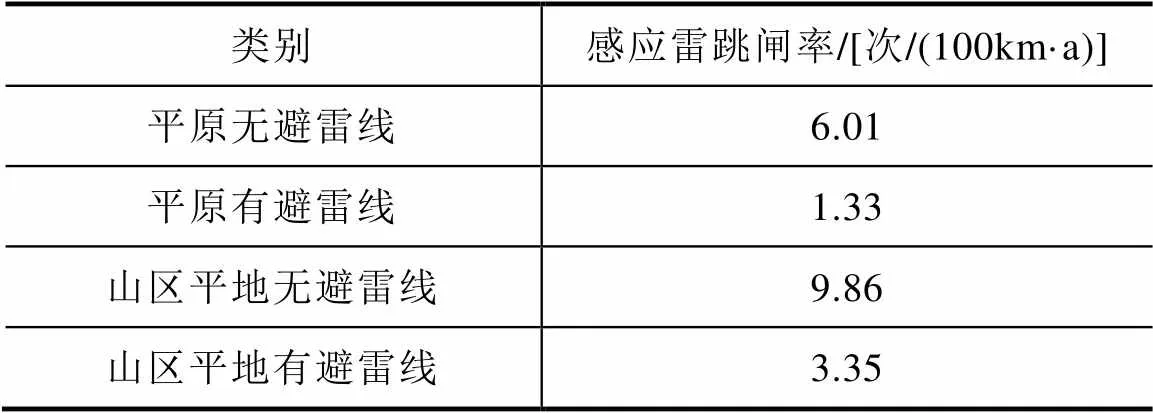
表4 地形倾角为0°时总雷击跳闸率计算结果

不同地形条件下，架空线路总雷击跳闸率随坡度的变化规律如图12所示。

由图12可知，地形对架空线路总雷击跳闸率的影响大小为：山谷＞山坡＞山脊。

当线路位于山谷时，线路总雷击跳闸率随坡度的增加而增大，无避雷线线路的总雷击跳闸率由9.96次/(100km·a)上升至10.64次/ (100km·a)，有避雷线线路的总雷击跳闸率由3.39次/(100km·a)上升至3.86次/(100km·a)。

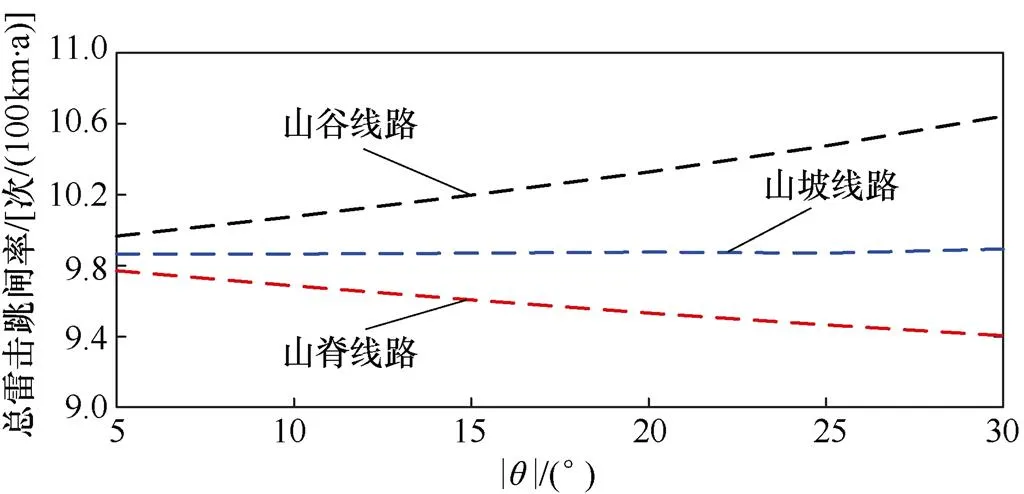
（a）无避雷线

（b）有避雷线

图12 山区架空线路总雷击跳闸率

当线路位于山坡时，线路总雷击跳闸率同样随坡度的增加逐渐上升，当坡度由5°上升至30°时，无避雷线线路总雷击跳闸率由9.86次/(100km·a)上升至9.89次/(100km·a)，有避雷线线路的总雷击跳闸率由3.36次/(100km·a)上升至3.56次/(100km·a)。

当线路位于山脊时，线路总雷击跳闸率随坡度的增加逐渐减小，当坡度由5°上升至30°时，无避雷线线路的总雷击跳闸率由9.77次/(100km·a)下降至9.4次/(100km·a)，有避雷线线路的总雷击跳闸率由3.32次/(100km·a)下降至3.26次/(100km·a)。

综合以上数据分析可知，对山区线路雷击跳闸率影响最大的地形为山谷地形，随着地形倾角（绝对值）的变大，山谷线路的总雷击跳闸率逐渐上升，最大增幅约为7.91%；地形倾角对于山坡线路的影响则几乎为0；处于山脊的线路雷击跳闸率则随倾角（绝对值）变大逐渐减小，最大降幅约为4.67%。

4 结论

本文提出了考虑地形的架空线路雷击跳闸率计算方法，分析了不同地形对35kV架空线路雷击跳闸率的影响规律，得到了以下结论：

1）架空线路的直击雷跳闸率大小顺序为：山脊线路＞山坡线路＞山谷线路。线路位于山脊处时，随着坡度的变大，直击雷跳闸率逐渐上升，相比于山区平地线路，其直击雷跳闸率最大增幅约为18.37%，而处于山坡与山谷的线路直击雷跳闸率则最大分别下降17.69%与53.74%。

2）架空线路的感应雷跳闸率大小顺序为：山谷线路＞山坡线路＞山脊线路。线路位于山坡或山谷处时，感应雷跳闸率随两侧的坡度增大而变大，最大增幅分别为5.49%和34.10%；线路位于山脊处时，随着坡度的增加，感应雷跳闸率逐渐下降，最大降幅为14.45%。

3）架空线路的总雷击跳闸率大小顺序为：山谷线路＞山坡线路＞山脊线路。相比平原地区，山区平地线路的总雷击跳闸率增大了64%左右；线路位于山坡处时，总雷击跳闸率几乎不随地形倾角发生变化；线路位于山谷和山脊时，随着坡度的增加，总雷击跳闸率分别上升与下降，最大增幅与降幅分别为7.91%与4.67%。

4）安装避雷线能有效降低线路雷击跳闸率，根据仿真计算结果，在平原地区与山区平地线路安装避雷线后，其总雷击跳闸率将分别下降77.87%与66.02%。

[1] 交流电气装置的过电压保护和绝缘配合设计规范: GB/T 50064—2014[S]. 北京: 中国计划出版社, 2014.

[2] 王录亮, 韩来君, 黄松. 海南强雷区典型配电线路差异化防雷措施研究[J]. 电气技术, 2022, 23(3): 103-108.

[3] 梁开旺, 冯珊. 10kV线路穿刺型避雷器安装配置方式实验与仿真研究[J]. 电气技术, 2022, 23(4): 102-108.

[4] 黎鹏, 肖盼, 屈莹莹, 等. 带长连续电流多重回击作用下500kV避雷器温升特性分析[J]. 电工技术学报, 2020, 35(增刊2): 603-611.

[5] 代杰杰, 刘亚东, 姜文娟, 等. 基于雷电行波时域特征的输电线路雷击类型辨识方法[J]. 电工技术学报, 2016, 31(6): 242-250.

[6] 李新, 武利会, 范心明, 等. 复杂地形条件下超高压错层塔上坡位上相绕击跳闸率计算[J]. 电瓷避雷器, 2020(5): 60-67.

[7] 杨跃光, 张建刚, 徐剑伟, 等. 基于改进EGM的±800kV输电雷电屏蔽性能优化配置研究[J]. 电瓷避雷器, 2020(1): 71-75, 81.

[8] 姚尧, 李健, 李涵, 等. 基于山区雷电先导发展的改进电气几何模型仿真研究[J]. 高电压技术, 2015, 41(5): 1550-1557.

[9] 赵国伟, 白洁, 李承, 等. 微地形环境下10kV配网雷害分析及防护措施优化配置[J]. 智慧电力, 2020, 48(4): 112-118.

[10] 王建军, 唐谟懿, 周力行. 地形地貌对配电线路雷害影响分析[J]. 电力科学与技术学报, 2017, 32(1): 151-156.

[11] 李瑞芳, 陶鑫, 杨雪, 等. 山区典型地形雷击地闪密度分布差异研究[J]. 高压电器, 2020, 56(5): 107- 113.

[12] 匡福志, 李霞, 钟湘平, 等. 山区配电线路塔位地形雷击风险分类[J]. 电力科学与技术学报, 2021, 36(4): 66-72.

[13] 傅景伟, 李小平, 姚尧, 等. 10kV架空配电线路常用防雷措施防雷性能对比研究[J]. 水电能源科学, 2019, 37(12): 132-135, 139.

[14] 黎鹏, 肖盼, 谌洪, 等. 地闪长连续电流对500kV直流输电线路故障重启动特性的影响[J]. 电网技术, 2021, 45(4): 1596-1604.

[15] 卢泽军, 赵淳, 王宇, 等. 地闪长连续电流对±500kV直流输电线路动作特性的影响[J]. 电瓷避雷器, 2020(6): 29-35.

[16] 曾程, 杨廷方, 李既明, 等. 某山区大跨越10kV线路分流系数量化分析及防雷改造[J]. 电瓷避雷器, 2020(4): 1-6.

[17] 祁汭晗, 蔡汉生, 廖民传, 等. 计及架空地线的配电线路雷电感应过电压模型及应用[J]. 电网技术, 2021, 45(6): 2413-2419.

[18] HOIDALEN H K. Calculation of lightning-induced voltages in MODELS including lossy ground effects[C]// International Conference on Power Systems Transients, New Orleans, USA, 2003.

[19] HOIDALEN H K. Analytical formulation of lightning- induced voltages on multiconductor overhead lines above lossy ground[J]. IEEE Transactions on Electro- magnetic Compatibility, 2003, 45(1): 92-100.

[20] 张金波, 彭晓宇, 王磊, 等. 复杂地形下架空线雷电感应过电压特性仿真研究[J]. 高电压技术, 2019, 45(11): 3708-3714.

[21] 马御棠, 王磊, 马仪, 等. 云南高海拔地区雷电活动分布规律的研究[J]. 电瓷避雷器, 2012(3): 46-50, 56.

[22] IEEE guide for improving the lightning performance of electric power overhead distribution lines: IEEE Std 1410—2010[S].

Simulation analysis on lightning strike characteristics of 35kV overhead lines in mountainous area

ZHANG Wenfeng1LI Zhiwei1ZHANG Guojian1LIN Gan2,3

(1. Dali Power Supply Bureau, Yunnan Power Grid Co., Ltd, Dali, Yunnan 671000; 2. Hubei Provincial Engineering Technology Research Center for Power Transmission Line (China Three Gorges University), Yichang, Hubei 443002; 3. College of Electrical Engineering & New Energy, China Three Gorges University, Yichang, Hubei 443002)

The typical terrains characteristics of Dali mountainous area overhead lines are analyzed in this paper. Based on the lightning activity data of lines collected by the lightning location system, the lightning resistance level and the trip rate of direct and induced lightning are calculated under typical terrain conditions such as ridge, hillside, valley and plain. The variation law of lightning trip rate of overhead line under mountainous terrain is obtained. The results show that the lightning trip rate varies greatly under different terrain conditions. The direct lightning trip rate of the line located on the ridge is larger and decreases with the decrease of the slope on both sides. However, the induced lightning trip rate of the line located in the valley is larger, which increases with the increase of the slope. Compared with plain areas, the lightning trip rate of mountainous lines is increased by about 64%.

overhead line; mountainous area; terrain; lightning trip rate; lightning induced overvoltage

2022-05-05

2022-05-24

张文锋（1984—），男，汉族，湖北宜昌人，工程师，研究方向为输电线路运行维护管理。

云南电网有限责任公司科技项目（0505002020030301SC00002）