卫星平台扰动对星载原子干涉重力梯度仪测量影响分析
2022-09-26段小春赵艳彬
祝 竺,段小春,廖 鹤,赵艳彬
(1. 上海卫星工程研究所,上海 201109;2. 华中科技大学 物理学院,武汉 430074;3. 重力导航教育部重点实验室,武汉 430074;4. 精密重力测量国家重大科技基础设施,武汉 430074;5. 南京航空航天大学 航天学院,南京 210016)
原子干涉重力梯度仪是探测地球重力场信号的重要仪器之一,一般由相隔一定距离的一对或多对原子干涉重力仪构成,其采用冷却的原子团作为检验质量来感应重力的作用,通过相位相干的拉曼激光对冷原子操控实现原子干涉,使原子所处叠加态的相位与运动路径中受到的重力加速度相关,检测原子的内态,通过干涉条纹拟合得到的相位便可获取重力加速度信息。再基于差分加速度的测量原理,获得所在位置处的重力梯度值Vij,即重力加速度g=[gx, gy, gz]随空间的一阶导,称为重力梯度张量,可表示为:

原子干涉重力梯度仪具有稳定性高、量程大、测量频带宽、低频白噪声谱平稳等诸多优点,成为近年来飞速发展的重力测量仪器之一,在大地测量、地球物理、资源勘探等领域发挥了重要的作用[1,2]。1998年,耶鲁大学研制出了地面首台原子干涉重力梯度仪,在1.4 m的基线长度下,测量灵敏度达到30 E/Hz1/2(1 E=10-9/s2)。经过二十多年的发展,国内外多家机构相继研制出了原子干涉重力梯度仪的地面样机。国内原子干涉重力梯度仪地面测量灵敏度目前达到100 E/Hz1/2(华中科技大学)[3]。
近年来,国内外研究小组均开始瞄准原子干涉重力测量的星载优势:一方面由于其测量灵敏度与原子干涉脉冲间隔T的平方成反比,在星载微重力环境下,T可以由地面的毫秒量级增大至秒量级,大大提升测量精度;另一方面,冷原子团和仪器框架(固连于卫星)同做自由落体运动,相对运动极小,有效规避了原子团触碰容器壁的风险,有利于星载设备的小型化。在该背景下,NASA与ESA均开展了原子干涉重力梯度仪星载测量的概念研究和初步设计[4,5],并指出理论上星载测量的潜在分辨率有望达到0.07 mE/Hz1/2[6],大大优于目前已成功在轨运行过的GOCE卫星上的静电式重力梯度仪(在轨分辨率10~20 mE/Hz1/2)。实验方面[7,8],JPL在NASA支持下开展了便携式星载原子干涉重力梯度仪的研制,用于未来空间计划的搭载;ESA研制了适用于不莱梅落塔的原子干涉仪样机,并开展了自由落体实验;法国ONERA实施了原子干涉重力仪的机载飞行实验。与此同时,国内中科院精密测量科学与技术创新研究院[9]、浙江大学[10]、浙江工业大学[11]、华中科技大学[12]、北京航天控制仪器研究所[13]等相关小组也详细阐述了原子干涉重力仪的空间应用前景,并开展了小型化可移动式样机和部组件的设计研制[14]。星载测量方案方面,法国巴黎天文台基于地面原子干涉重力梯度仪上抛下落式的测量原理,提出了一种基于差分对抛式的星载原子干涉重力梯度仪方案[15],并估计梯度仪测量噪声3.5 mE/Hz1/2。该方案可以同时测量对角梯度分量和卫星角速度信息,但是该类型的梯度仪测量噪声受限于仪器尺寸和原子抛出速度,并且为了测量卫星角速度,增大了系统结构的复杂度。针对该问题,在以往的工作中[16,17],我们分析了地面与星载失重环境下原子干涉重力梯度仪的测量机理差异,提出了一种适用于星载环境的“零初速释放”式的原子干涉重力梯度仪测量方法,并预估该梯度仪测量噪声有望达到1 mE/Hz1/2左右。实际空间应用中,卫星平动自由度和转动自由度的干扰加速度对高精度的重力梯度仪测量将产生一定的影响,主要体现在:(1)卫星平动自由度的干扰加速度会引入质心偏差以及梯度仪基线长度变化;(2)卫星转动自由度在绕垂直轨道平面的轴向上会存在一个较大的转动角速度(轨道角频率),导致原子团所在测量基线方向与拉曼激光方向发生偏离,贡献离心力与科里奥利力。这些干扰加速度分为两种:一种是时域的常值干扰加速度,会带来重力梯度测量的系统误差,这部分可通过数据处理进行扣除和抑制;另一种是干扰加速度的波动,会引入重力梯度测量的测量噪声,可在频域通过噪声功率谱密度体现。本文主要分析后者,值得注意的是,对于星载重力梯度测量的测量噪声而言,其贡献因素很多,包括梯度仪仪器噪声、卫星平台噪声等。其中占主导作用的是梯度仪仪器噪声,其噪声本底主要受限于量子投影噪声(决定了噪声极限),可控制在mE/Hz1/2量级,该部分内容在以往的工作中已开展了详细的分析[18]。目前国内外对于星载原子干涉重力梯度仪的噪声分析主要集中在仪器噪声,例如拉曼光相位噪声、探测噪声、光强噪声等。然而在星载条件下,除了仪器噪声外,卫星平台贡献的噪声也不可忽略,将直接影响原子干涉重力梯度仪的测量。因此在该背景下,本文开展了卫星平台干扰加速度对星载原子干涉重力梯度仪测量的影响分析研究:首先介绍了“零初速释放”式的星载原子干涉重力梯度仪测量原理,其次分析了卫星平台平动自由度和转动自由度的干扰加速度对原子干涉重力梯度仪测量的影响,并给出了相应的解决途径和残余噪声贡献,为未来星载原子干涉重力梯度仪的空间工程应用提供理论支撑。
1 “零初速释放”式的星载原子干涉重力梯度仪测量方法
对于原子干涉重力梯度测量,地面采用的是“上抛下落”式的测量方法:采用磁光阱(Magneto Optical Trap, MOT)将原子冷却囚禁后,通过竖直上抛不同高度的冷原子团,在地表1g重力加速度的作用下原子下落,并用激光操控冷原子团使之发生干涉,继而感测出不同高度处的重力加速度,通过差分重力加速度信息来获取竖直方向上的重力梯度分量Vzz,如图1所示。

图1 原子干涉重力梯度仪地面测量方法Fig.1 On-ground measurement method of atom-interferometry gravity gradiometer
空间环境下原子失重,与仪器框架(固连于卫星)同做自由落体运动,原子团与卫星几乎相对静止(仅存在由于卫星受到的大气阻尼力、姿态变化等干扰引起的微小相对运动),此时可利用空间这种独特的微重力环境,当原子团冷却囚禁后,不需要给定一个初速度抛出再下落,而是直接零初速的释放原子团,再通过拉曼激光操控使之发生原子干涉来完成测量,如图2所示。

图2 原子干涉重力梯度仪星载测量方法Fig.2 Measurement method of space-borne atom-interferometry gravity gradiometer
“零初速释放”测量方法如下:第一步,沿卫星质心对称放置三对MOT,分别置于卫星的X、Y、Z轴。第二步,在MOT里完成原子的囚禁和冷却。第三步,关闭线圈电流,使MOT失效,让原子处于自由漂浮状态。第四步,沿每个测量基线方向,用拉曼激光操控原子实现干涉,通过测定干涉相位差Δφ获得同一方向上的差分加速度Δa,可表示为:

其中keff是拉曼激光脉冲的有效波矢,T是激光脉冲间隔。差分加速度Δa不仅包含了待测的重力梯度值,还含有卫星旋转引入的离心力和科里奥利力,这是因为在地心坐标系下,对单个干涉仪的原子团用牛顿第二定律,有:
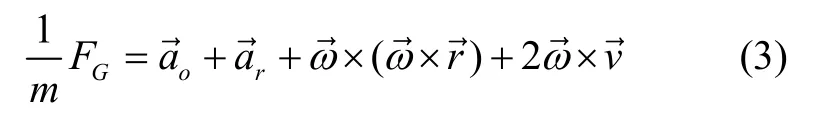
其中等式左边FG表示地球质量体对原子的万有引力,m表示原子的质量。右边第一项表示卫星在沿着地球公转的轨道上运行时,对应的卫星质心相对于地心惯性坐标系的飞行加速度,第二项是在卫星质心坐标系下原子相对卫星的加速度,也是原子干涉仪的输出;第三项和第四项分别为牵连加速度和科氏加速度,其中表示卫星绕其质心自转角速度,和分别表示原子在卫星质心坐标系中的位矢和速度。由于原子相对于卫星的速度接近于零,在本节理论推导中,科氏加速度暂时忽略。因此对于同一测量基线上的一对干涉仪(分别用下标1和2表示),其输出为:
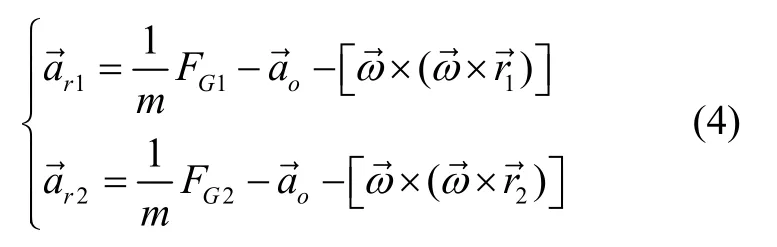
因此原子重力梯度仪的差分加速度输出可表示为:


其中Vii表示待测的重力梯度分量,ω2=ωx2+ωy2+ωz2表示卫星角速度,下标i=x,y,z表示测量方向。因此需要采用星敏、陀螺仪等测量卫星角运动信息,并在差分加速度中扣除,以得到对角梯度分量Vxx、Vyy、Vzz的值。
相比于地面测量方法而言,该空间测量方法具有诸多优势:(1)星载条件下,原子失重处于自由漂浮状态,测量的是原子团相对于卫星的加速度,在500 km以下的近地轨道,该加速度不超过10-6m/s2量级,因此原子团与卫星几乎相对静止,此时不需要采用地面上抛原子团的方法进行测量,直接用拉曼激光与两团漂浮的原子进行作用,可有效避免原子团在短时间内触碰容器壁的风险,获得较长的干涉脉冲间隔,提高测量精度,利于仪器的小型化研制。(2)该方法不再局限于地面仅竖直方向梯度分量Vzz的测量,空间中可测量Vxx、Vyy、Vzz多个梯度分量,获得更丰富的重力梯度信息。
2 卫星平台扰动对原子干涉重力梯度仪的测量影响
重力梯度测量卫星的平台干扰加速度主要分为平动干扰加速度和转动干扰加速度。平动自由度的干扰加速度主要来源于低轨大气阻尼、太阳光压等。转动自由度的干扰加速度主要由卫星姿态机动产生。下面分别进行讨论。
2.1 卫星平动自由度的干扰加速度影响
理论上,卫星质心与梯度仪的基线中心重合,如图2所示。实际中,当原子团在空间释放后,处于失重自由漂浮状态,外界微小的干扰加速度将导致卫星质心与梯度仪基线中心发生偏离,且同一方向上两团原子之间的距离即梯度仪基线长度也随之发生变化。
(1)共模干扰加速度影响分析
当同一方向上的一对原子干涉仪受到外界共模干扰加速度时,会导致卫星质心与梯度仪基线中心发生偏移,如图3所示。

图3 共模加速度扰动导致的质心偏差Fig.3 Center of mass offset induced by common-mode acceleration disturbances
低轨卫星的共模加速度主要来源于外界大气阻尼扰动,由此产生的质心偏差Δd可估算为:
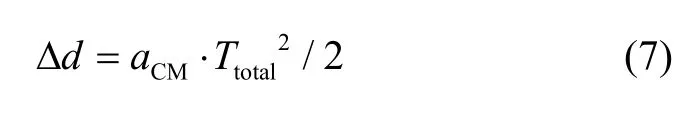
其中aCM是卫星的共模加速度,在250 km以下的轨道高度,该值不超过1×10-5m/s2[17],Ttotal≈ 2T是原子团零初速释放后自由漂浮状态下干涉测量的时间,根据重力场测量空间分辨率与干涉脉冲间隔T之间的关系,Ttotal最大可设置为13.4 s[17],根据式(7),产生的最大质心偏差Δd约为0.9 mm。对于卫星重力梯度测量模式而言,共模干扰加速度可通过差分测量抑制掉,因此并不贡献重力梯度测量噪声,但会产生梯度仪中心和卫星质心的偏差,主要影响低轨卫星无拖曳控制系统的阻尼补偿,最大质心偏差一般控制在cm级即可[19],故0.9 mm的质心偏差在允许的误差范围内。
(2)差模干扰加速度影响分析
同一基线上的两个干涉仪测量的差模加速度会导致测量基线的长度发生变化,如图4所示。

图4 差模加速度扰动导致的基线长度变化Fig.4 Baseline length change induced by different-mode acceleration disturbances
差模加速度aDM主要来源于重力梯度和离心加速度的影响,在i方向上产生的梯度仪基线长度偏差△Li可表示为:
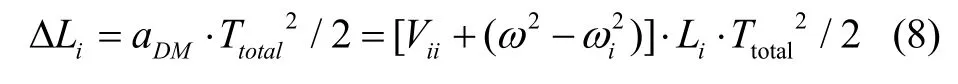
250 km轨道高度处最大的重力梯度值来源于地心径向Vzz≈ 2740 E,最大角速度来源于垂直轨道平面方向,由于卫星对地指向三轴稳定,故该方向存在一个较大的公转角频率ωy≈ 1.2×10-3rad/s,在基线长度Li= 0.5 m的情况下,产生的梯度仪基线长度偏差约为△Li= 0.2 mm。该偏值可在数据后处理中扣除或者在通过π脉冲时改变有效波矢的大小来补偿[20]。而基线长度偏差的波动会对重力梯度的测量噪声产生影响,这主要取决于轨道高度处的差模加速度的波动大小,可得:

根据ESA给出的GOCE在轨L1b数据[21],可得250 km的轨道高度处差模加速度在频域的功率谱密度约为δaDM(f)=10-11m/s2/Hz1/2,由式(9)可计算出基线长度的波动约为δLi(f)= 0.9 nm/Hz1/2,由引入的重力梯度噪声约为:
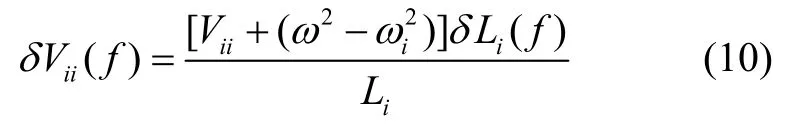
而飞行方向和垂直轨道平面方向的重力梯度值约为地心径向的一半,Vxx≈ Vyy≈ 1370 E。对于三轴稳定对地指向卫星而言,最大的卫星角速度来源于垂直于轨道平面方向ωy≈1.2×10-3rad/s,其他两轴的卫星角速度ωx和ωz约为10-6rad/s量级。根据式(10),在Li=0.5 m的基线长度下,贡献的最大重力梯度测量噪声来源于地心径向,约为δVzz(f)=8×10-3mE/Hz1/2。飞行方向和垂直轨道平面方向贡献的重力梯度测量噪声分别为δVxx(f) = 5×10-3mE/Hz1/2和δVyy(f)=2.5×10-3mE/Hz1/2。
2.2 卫星转动自由度的干扰加速度影响
卫星重力梯度测量主要是获取式(1)中重力梯度张量矩阵的三个对角分量Vxx、Vyy与Vzz,即在轨道高度处,测量沿飞行方向、垂直轨道平面以及地心径向三个方向上(坐标定义见图2)的重力梯度分量值,因此卫星姿态需设置为三轴稳定对地指向,此时卫星绕垂直轨道平面即Y轴存在一个较大的公转角频率ωy≈ 1.2×10-3rad/s,而激光器固连于卫星,导致在测量过程中,拉曼激光打出的方向跟随卫星旋转,偏离冷原子团所在的梯度仪基线方向,影响测量结果。为解决该问题,可采用“反射镜+驱动电机”的方法补偿卫星角速度,通过驱动电机实时调整激光反射镜,让激光束的方向始终对准原子团所在基线方向,如图5所示。该方法在地面测量中多用于补偿地球自转影响。然而与地面不同的是,星载测量中,由于卫星三轴稳定对地指向,存在一个较大的公转角速度1.2×10-3rad/s(地面需要补偿的地球自转速度仅为10-6rad/s量级),且空间中的干涉测量时间Ttotal远大于地面。因此要求驱动电机的转速达到ω=1.2×10-3rad/s,且能够补偿的角度范围大于ω·Ttotal=1.6×10-2rad。

图5 卫星存在角运动情况下的激光束调整策略Fig.5 Laser Beam adjustment strategy in the presence of satellite angular motion
补偿后的残余角速度,将对重力梯度仪产生离心力与科里奥利力,带来额外的测量误差,下面分别讨论。
(1)离心力的影响分析
对于离心加速度项,由于卫星角速度属于低频角运动,一般对于频率低于10 Hz的角运动,航天器主要采用高精度陀螺仪或光学敏感器等组成的高精度的卫星测姿系统来实现。卫星角速度的测量噪声δω贡献的梯度测量噪声可表示为:

其中下标i、j、k满足右手螺旋法则。由于卫星三轴稳定对地指向,因此卫星Y轴存在一个较大的公转角频率ωy≈ 1.2×10-3rad/s,而X与Z轴的角速度较小,约在10-6rad/s量级。空间原子干涉重力梯度测量对振动等环境较为敏感[22],因此星上陀螺仪需尽量采用无机械振动的陀螺仪如激光陀螺仪、原子陀螺仪等。例如星载原子陀螺仪灵敏度可达δωi= 10-12rad/s/Hz1/2[23]。因此根据式(11),可计算出卫星角速度测量噪声贡献的梯度测量噪声不超过2.4×10-3mE/Hz1/2。
(2)科里奥利力的影响分析
对于科里奥利加速度项,主要通过卫星角速度耦合原子残余速度而产生。一方面,采用图5中“反射镜+驱动电机”的方法补偿卫星角速度ω,减小科里奥利加速度项的影响,另一方面,需对原子残余速度提出要求。对补偿后的残余科里奥利加速度建模,可表示为:

式中下标i、j、k满足右手螺旋法则。ωj与ωk分别为卫星j方向和k方向补偿后的残余角速度,Δvj与Δvk分别为j方向和k方向的测量基线上两团原子团相对于卫星的速度之差,δvj与δvk分别为j方向和k方向上单个原子团相对于卫星的残余速度。根据国外实验研究结果,补偿后的卫星残余角速度可降低60倍[24]。因此经补偿后,卫星Y轴的最大角速度可由ωy≈1.2×10-3rad/s降低至2×10-5rad/s。此时为达到1 mE/Hz1/2的梯度测量精度,则要求原子在X与Z方向的速度扰动小于δvx=δvz=10 nm/s/Hz1/2。而原子零初速释放后自由飘浮,单个原子团相对于卫星的残余速度非常微小,主要来源于三对打向原子团的激光功率的不稳定性,这就对激光束的功率差提出了指标要求。设激光功率比为r=P2/P1≈1+ΔP/P,其中P1≈P2=P为激光的平均功率,ΔP = P2- P1为激光功率之差。建立激光功率差与原子速度漂移之间的关系如下[25]:每出现1%的激光功率比变化,就会导致20 μm/s的原子速度漂移。因此本方案中要求原子速度漂移小于10 nm/s/Hz1/2,这就意味着激光功率差ΔP/P需小于5×10-6/Hz1/2。
2.3 平台干扰加速度影响分析小结
综上所述,卫星平台平动自由度和转动自由度的干扰加速度对星载原子干涉重力梯度仪的测量噪声贡献如表1所示。需要说明的是,在考虑重力梯度测量的干扰加速度时,原则上应利用灵敏度函数结合干扰加速度的噪声谱进行评估,设时域灵敏度函数对应的Fourier变换为G(f),则对单个原子干涉重力仪来说,其相移波动与干扰信号的噪声功率谱有以下关系:

表1 卫星平台干扰加速度贡献的原子干涉重力梯度仪测量噪声Tab.1 Noise contribution for space-borne atom - interferometry gravity gradiometer caused by satellite platform disturbances

其中Sa(f)表示干扰加速度的单边噪声功率谱。用于反演地球重力场的星载重力梯度仪,主要关注的是低频段(0.1 mHz~100 mHz)的重力梯度信号。在低频段,/(2π T2f )2≈ 1,因此可近似认为该干扰直接影响单个原子干涉仪,从而引入原子干涉重力梯度测量的噪声。
3 总 结
低轨对地三轴稳定卫星的平台干扰加速度会对冷原子干涉重力梯度仪的测量产生影响:一方面,平动自由度的干扰加速度将引入两部分影响,其中共模干扰加速度导致梯度仪质心产生0.9 mm的偏差,影响无拖曳控制系统的补偿,但不影响重力梯度测量,差模干扰加速度导致基线长度发生变化,对原子干涉重力梯度测量的噪声贡献仅在10-3mE/Hz1/2量级,可忽略不计;另一方面,转动自由度的干扰加速度带来激光方向偏离,引入额外的离心力与科里奥利力,可采用“反射镜+驱动电机”的方法补偿卫星角速度并采用高精度的星载陀螺仪测量出卫星角速度,在原子速度漂移小于10 nm/s/Hz1/2,激光功率差小于5×10-6/Hz1/2的条件下,该部分引入的噪声影响可控制在1 mE/Hz1/2。且要求驱动电机的转速达到1.2×10-3rad/s,补偿的角度范围大于1.6×10-2rad,该指标主要受限于驱动电机执行反馈的响应速度和反馈范围,将在后续工作中开展详细分析。
