基于神经网络的低氮燃气锅炉故障诊断研究

赵培庆

(北京北燃环能科技发展有限公司，北京 100011)

低氮燃气锅炉对锅炉房系统来说，属于重大关键设备，也是故障发生频繁的部分[1]。正确监测锅炉的状态，预测可能发生的故障，对维护人员及早发现故障，尽快处理故障有很大的帮助，并对锅炉房重大设备的安全性、提高设备的利用率、减少非计划停机的次数和时间等起到积极作用，还能有效降低检修费用，提高锅炉房的经济效益[2-3]。

根据低氮燃气锅炉的状态参数历史数据训练BP神经网络，然后将此信息与当前测量的锅炉运行参数数据进行比较，以确定相应的故障；充分利用BP神经网络的自学习、非线性、并行计算和容错的能力，提高了低氮燃气锅炉故障诊断的快速性和准确率[4]。

1 神经网络结构和算法

BP神经网络已广泛应用于非线性建模、函数逼近、系统辨识和分类等方面,但对实际问题,其模型结构需由实验确定。

1.1 BP神经网络的结构

BP神经网络是一种单向传播的多层前向网络，其结构如图1所示。网络由输入层、一层或多层隐含层和输出层组成。

图1 BP神经网络结构图

1.2 BP神经网络的算法

在BP神经网络中输入层得到刺激后，会把他传给隐含层，至于隐含层，则会根据神经元相互联系的权重并根据规则把这个刺激传给输出层，输出层对比结果，如果不对，则返回进行调整神经元相互联系的权值。这样就可以进行训练，最终学会。在 BP 学习算法中，输入层，输出层和隐含层权值调整方式都是一样的。由三个条件决定，它们分别是：学习效率，输入层，输出层和隐含层的各层误差信号和各层输入信号X/Y。其中最为重要的是输出层误差信号，它直接意味着和实际期望结果的差异，代表着与预期结果的差距，而前面的各层的误差都是从后往前传递计算的误差。

2 算例和分析

2.1 训练样本

将低氮燃气锅炉出水和回水温度、出水压力、水位和燃气压力以及排烟温度、烟气NOx含量7个系统参数作为网络的输入向量X=(x1,x2,x3…,x7)，输出向量为故障原因Y=(y1,y2,y3…,y5)，从而建立系统参数与故障原因之间的映射关系，如表1所示。

表1 系统参数与故障原因映射关系表

网络的样本经过数据变换处理、提取特征参数作为样本集如表2所示，输出为样本对应故障原因Yi，如果对应编号的项取1，表示该故障原因发生，否则取0，表示该故障原因不发生，若输出全为0，表示故障没有发生。

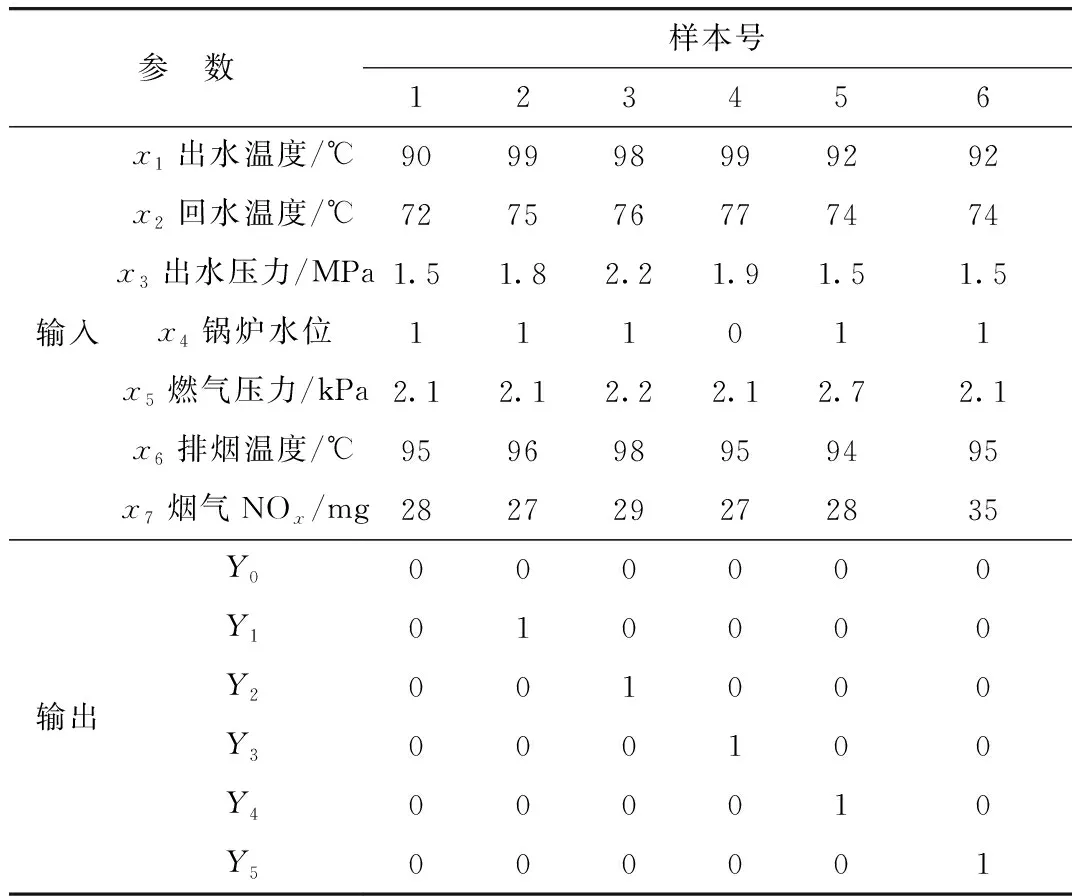
表2 故障类型与样本分析表

2.2 网络的训练和测试

将采集的锅炉参数及相应的故障原因作为学习样本。一般将数据分为两部分，一部分作为网络训练，一部分作为测试。

为简单起见，采用5级模糊算子对输入参数进行处理，模糊算子特征值如表3所示。

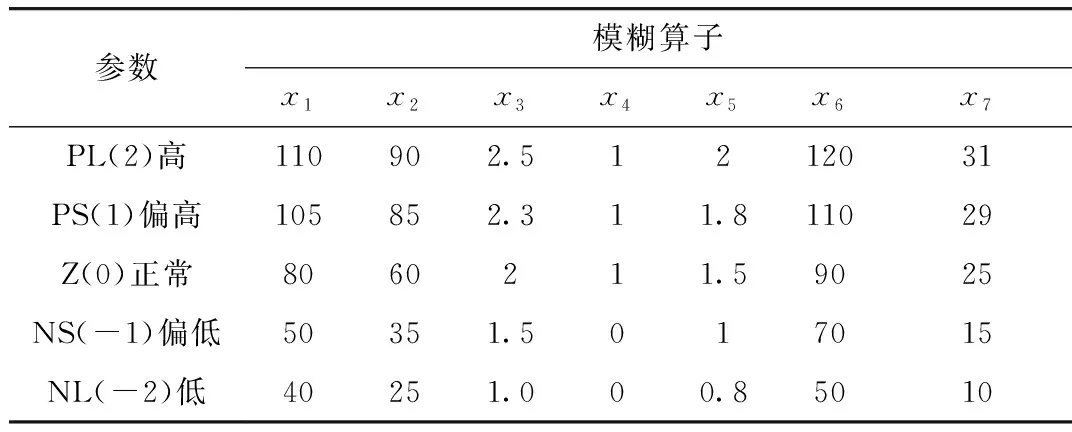
表3 模糊算子特征值

根据各对应故障下的运行参数分别计算对应的模糊算子，根据最大隶属度原则，选取5个隶属度最大的一个作为该故障参数下的模糊算子，计算结果如表4所示。

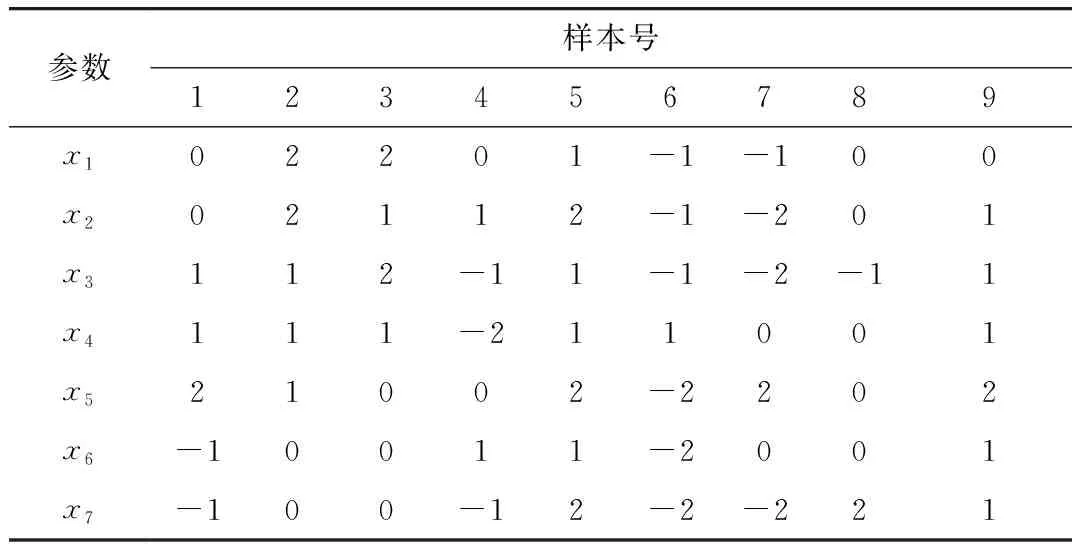
表4 参数模糊化后的算子

网络经过训练后便具备了诊断故障的能力。训练样本的测试结果如表5所示。从表5的诊断结果数据中可以看出,人工神经网络具有很高的诊断精度。经过更多组样本的测试,诊断结果表明网络同时也具有非常好的鲁棒性。

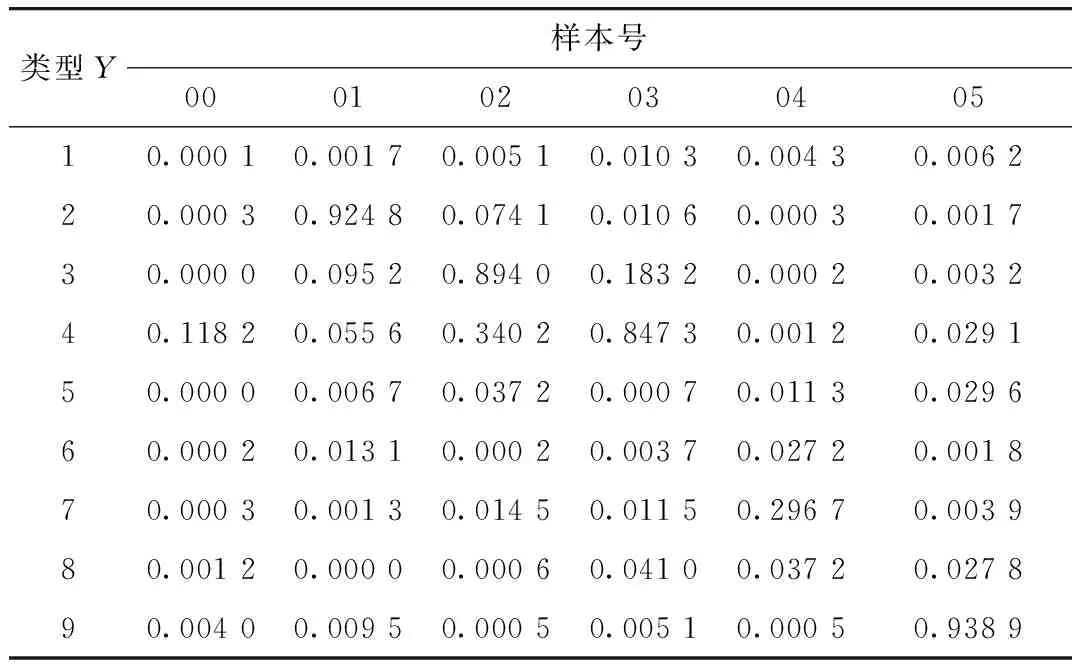
表5 训练测试结果

2.3 误差分析

为了提高神经网络的收敛速度,防止出现局部极小点,通过在Matlab仿真平台上进行反复训练和比较后,发现网络在学习速率为 0.7，动量常数为 0.2 时样本训练的结果可 达到很高的精度,故障平均误差保持在0.01 以下。对训练过程进行多次仿真，得出训练次数与均方误差的关系如图2所示。

图2 训练次数与均方误差关系图

3 结 论

基于BP神经网络故障诊断的方法能有效地克服单一神经网络存在的结构庞大、样本准备和网络学习困难、可靠性和精度差等问题。通过Matlab仿真证实该方法对于低氮锅炉系统故障诊断有较高的精度和实用性。