最小错误概率Bayes分类在杨梅图像数据分类中的运用*
2022-09-26卢巍王昕
卢巍 王昕
1.昆明文理学院信息工程学院;2.云南轻纺职业学院
本文以Bayes分类为基础理论,结合杨梅图像自身的特点和它所服从的统计学特性,得到一种基于最小错误概率Bayes决策的分类方法在杨梅图像数据分类中的运用。文章首先介绍基于最小错误概率Bayes决策理论,然后从理论上推导其在杨梅图像数据中分类数据的运用,最后通过实验分析其运用的实际效果和各种不同参数对分类效果的影响并得出结论。
模式识别与信号处理、概率统计、数字图像处理等学科有着密切的联系,其中很多分类方法较为成熟且广泛的运用于数据分类中,并在许多实际问题和多种不同分布数据分类中取得了良好的效果。其中Bayes分类一直在这些分类方法中占据着重要地位,它是模式识别中最主要的统计处理方法,其成熟的理论基础和对许多学科问题高度的适应性使得它被广泛运用于许多不同的学科中,并衍生出各自学科中独立的算法[1]。
1 最小错误概率BAYES分类原理
在决策论的诸多方法中,基于最小错误概率Bayes分类是一种较成熟并得到广泛运用的分类方法,它的基本原理是基于最小错误概率Bayes决策理论。
在许多实际的分类问题中,人们所关心的最重要的问题是尽可能的减小分类错误,以达到最小的错误分类概率,这就要求建立一个能得到最小错误概率的决策方法,以达到最终的分类目的。在最小错误概率Bayes决策中,先验知识是进行分类的基础条件。所谓先验知识,是在分类前所能获得的模式信息,通过概率论方法将其转化为先验概率,成为一种或多种模式特征为识别所用。可是,在实际的识别问题中,先验知识所能提供的信息量往往太少,仅仅通过先验知识和由其转化得到的先验概率,无法对模式做出最有效和准确的判断。这时,为提高分类准确率,一个可行的方法是将先验知识和由其转化得到的先验概率转化为后验概率,并运用后验概率所提供的信息去判决,以提高判决的准确率,得到更好的判决效果[2]。
Bayes法则为上述思想提供了可行的理论依据。假设要研究的问题中有N个类别,已经知道先验概率p(ωi),为简化问题,只考虑用一个模式特征x来进行分类,假定所选取的特征x是一个连续随机变量,其类别状态条件概率密度可以表示为p(x│ωi),它的意义是当类别状态为ωi时,x的概率密度函数。对于两类模式ω1和ω2的情况,x的类别状态条件概率密度函数是不相同的。他们的差别就可以用来反应两类模式的差别。给定一个观察样本x,根据Bayes公式把先验概率转化为后验概率。
对于一个待分类模式,得到一个观测值x,可能出现以下两种结果,如式(1)、式(2)所示:

当公式(1)成立的时候,将倾向于将待分类模式判入类别状态ω1,反之,当公式(2)成立的时候,将倾向于将待分类模式判入类别状态ω2。这样,就能使分类的错误概率最小。可是,在实际运用中,两次观测到完全一样的x值的可能性,非常小,同时,模式特征x是一个随机变量,运用Bayes法则后,每当观察到一个模式时,得到特征x,接着就利用后验概率做出分类判决,这个时候,必然会带来一定的错误判决风险,也就相应的带来错误判决概率[3]。为了提高分类正确率,自然期望错误判决的概率最小,这里可以从模式的x值上做出分析,模式的x值不同,其相应得到的后验概率必然不同,从而错误概率也不同,所以分类的错误概率p(e│x)是随机变量x的函数,当观察到大量模式时,对其做出错误判决的概率p(e)应该是p(e│x)的数学期望。对于每次观察到的特征值x,p(e│x)如果尽可能小的话,积分也必定是尽可能小的。这也从另一个角度证实了Bayes决策法则,当p(ω1│x)>p(ω2│x)时,将待分类模式判入ω1类,反之亦然。
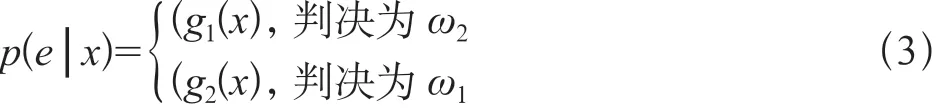
运用式(3)决策方法,可以构造分类器。当然,判别函数不是唯一的,比如将判决函数乘上一个或者加上一个正的常数等类似的处理时,所得到的新的判决函数具有相同的判决结果。可是,经过这些处理后得到的新的判决函数有可能将大大简化判决过程的计算量[4]。
2 最小错误概率Bayes分类杨梅图像数据
根据上述对最小错误概率Bayes决策理论的分析,运用所得到的判决函数,得到将最小错误概率Bayes决策理论运用于杨梅图像数据中的分类器,并设计编程实现算法。研究团队在前期拟合优度研究中发现,纯净无杂色的杨梅图像样本可以用K分布来描述,加入背景后,样本拟合优度统计特性偏向K+K分布。为验证最小错误概率Bayes分类器在K+K分布中的运用效果,总共进行了三组不同的实验,期望能证明其分类的有效性并找出此方法在K分布运用中存在的不足[5]。其中实验一目的是验证最小错误概率Bayes分类器运用于K分布中的分类效果;实验二目的是检验K+K分布中,不同形状参数和尺度参数对最小错误概率Bayes分类器分类效果的影响;实验三目的是检验不同形状参数和尺度参数的训练样本对最小错误概率Bayes分类器分类效果的影响。
在实验中,所选取的训练样本为具有以下参数的四组K分布样本,如表1所示为所选取样本的参数列表。
从表1中可以看出,训练样本一、二的形状参数较为接近,而训练样本三、四的形状参数相差较大,在这里,笔者并没有选取λ大于10的训练样本,这是由于,在实际杨梅图像中,其所服从的K分布的λ值很少有大于10的情况。同时使用3组不同参数和混合权重的K+K分布数据为待测样本,如表2所示为测试样本的参数对照表。
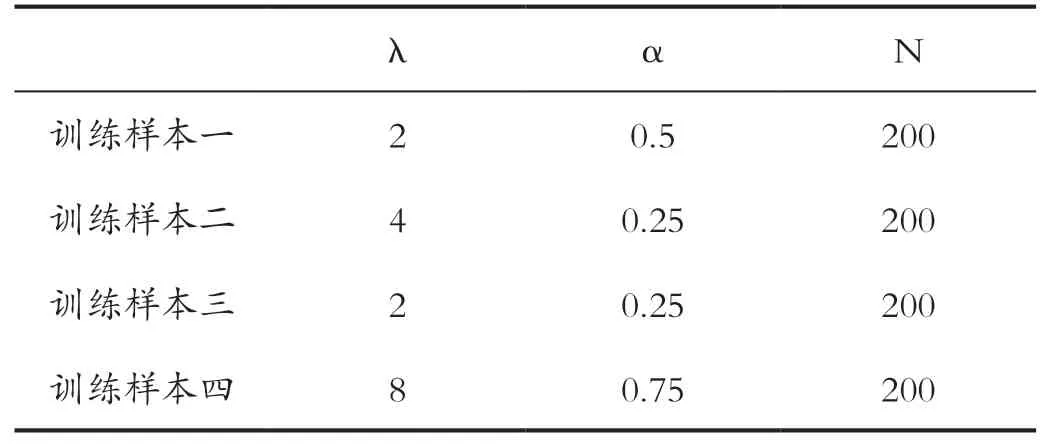
表1 训练样本参数对照表Tab.1 Comparison table of training sample parameters
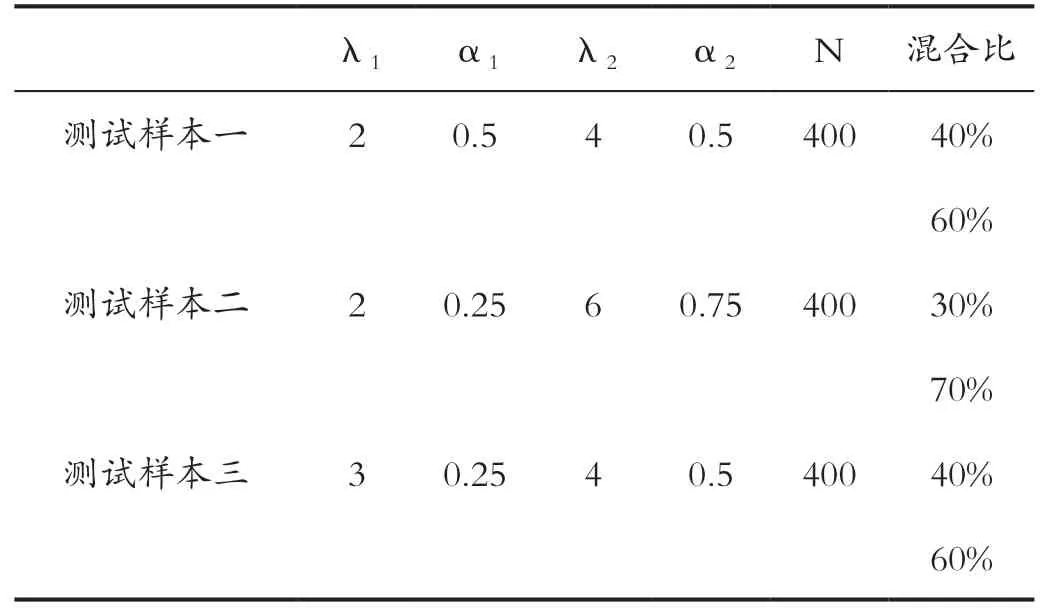
表2 测试样本参数对照表Tab.2 Comparison table of test sample parameters
其中,测试样本一、二参数值和其混合比均有不同,这样数据的选择有利于我们验证最小错误概率Bayes分类器的有效性。而测试样本三的参数值较为接近,这时,我们可以理解为其数据的混合度较高,这样的数据将考验分类特征提取有效性,同时有利于我们了解最小错误概率Bayes分类器在如此环境下的有效性。
实验1:验证最小错误概率Bayes分类器分类效果。为检验Bayes分类对混合K分布数据的分类效果,运用训练样本一和训练样本二对所设计分类器进行学习,并对测试样本一和测试样本二进行分类,其分类结果如表3所示,表中显示分类正误个数和分类正确率。
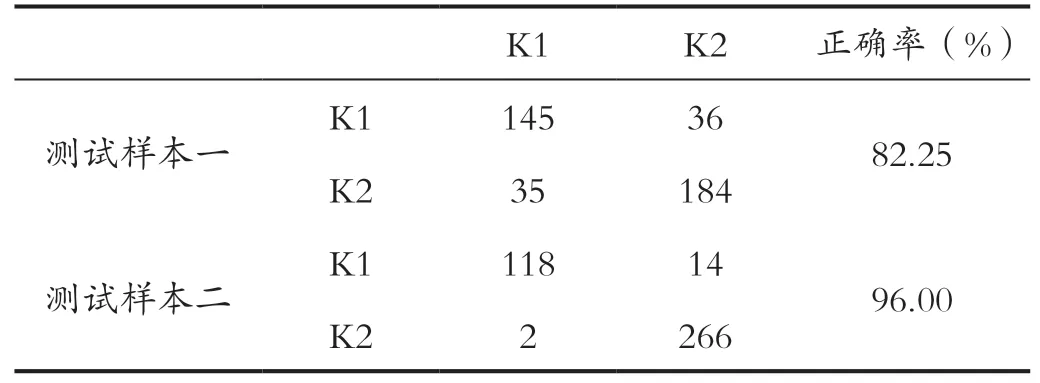
表3 Bayes分类对混合K分布数据的分类效果表Tab.3 Classification effect table of Bayes classification on mixed K distribution data
从表3中可以看出,所设计的最小错误概率Bayes分类器对测试样本一和测试样本二的分类正确率均达到80%以上,可以实现对混合K分布数据的分类,分类正确率均在80%以上,分类效果较好。
实验2:检验K+K分布不同参数对分类器效果的影响。为检验混合K分布不同形状参数和尺度参数对Bayes分类器分类效果的影响,笔者运用训练样本一和训练样本二对分类器进行训练,并对测试样本一和测试样本三做对比实验。具体分类结果如表4所示,表中显示分类正误个数和分类正确率。
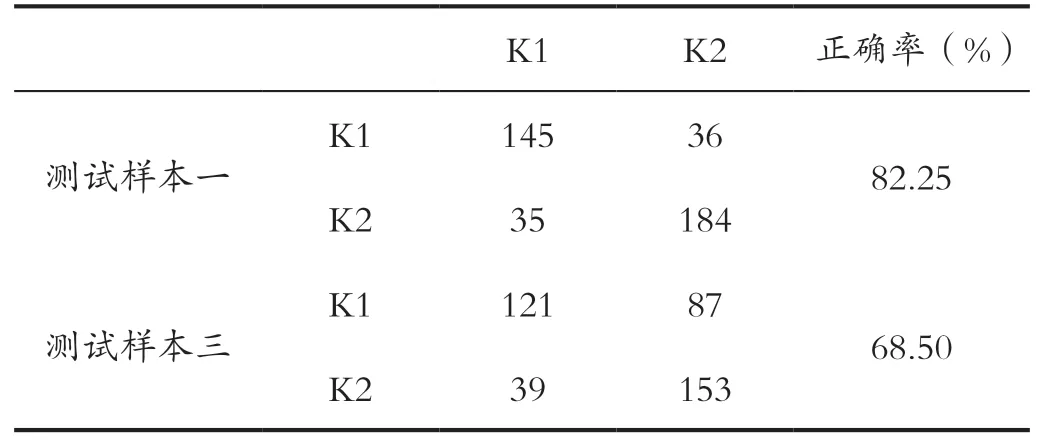
表4 验证测试样本不同参数分类效果表Tab.4 Table of classification effect of different parameters of validation test samples
从表4中可以看出,当混合K 分布形状参数和尺度参数较为接近,这时候我们也可以说混合K分布混合度较高时,算法有效性将受到较大影响,在对测试样本三的测试中,由于所混合的两个K分布其λ值一个为3,一个为4,只相差1,其α值也较为接近,此时,分类正确率不足70%,可以认为,在这样的情况下,所设计的最小错误概率Bayes分类器失效。同时,实验中还分别统计了对K1和K2的分类正确率,其中对K1的分类正确率不足60%。
实验3:检验不同训练样本对分类器分类效果的影响。在运用传统的Bayes分类器进行分类中,训练样本的选取效果将直接影响分类效果。在混合K分布的分类中,实验2已经验证测试样本的形状参数和尺度参数将对分类效果产生巨大影响,在本实验中,选取不同形状参数和尺度参数的训练样本,以证实不同的训练样本对分类结果的影响。实验中,选取训练样本一和训练样本二为一组,训练样本三和训练样本四为一组,对测试样本一进行分类,其分类结果如表5所示,表中显示分类正误个数和分类正确率。

表5 实验三分类效果表Tab.5 Classification effect table of experiment 3
从表5中可以看出,不同训练样本对Bayes分类结果也将产生影响,分析其原因,主要是训练样本的参数选择直接关系到所提取特征的有效性,同时不同的训练样本参数,也会对判决函数产生重大影响,经过多次实验证实,在训练中,应选取形状参数和尺度参数较为接近,但又不至于引起混淆的训练样本,这样的训练样本将有助于提高分类效果。
3 结语
总之,运用最小错误概率Bayes分类器可以有效的将杨梅图像数据分类,以便于对其分布统计特性等问题做进一步研究。由于在运用最小错误概率Bayes分类器分类时,所选取分类特征的有效性是能否实现正确分类的一个重要条件,而当测试样本的参数较为接近时,将对分类特征的选取提出较为苛刻的要求,此时,所选取的分类特征是否仍然有效,是否足够,都将严重影响到分类正确率,甚至可能导致分类器失效。
引用
[1] 曾平平,李林升.基于卷积神经网络的水果图像分类识别研究[J].机械设计与研究,2019,35(1):23-26+34.
[2] 李思奇,吕王勇,邓柙,等.基于改进PCA的朴素贝叶斯分类算法[J].统计与决策,2022,38(1):34-37.
[3] 张文倩,王瑛,张红梅,等.基于变分贝叶斯的数据分类算法[J].空军工程大学学报(自然科学版),2017,18(2):89-94.
[4] 孟大伟.基于纹理信息的水果图像识别方法仿真研究[J].计算机仿真,2011,28(12):293-295+322.
[5] 卢巍,薛瑞璇,邢孟江.KS检测在卫星交通图像数据分类中的运用[J].福建电脑,2018,34(3):12-13.
