零极点特性在数字滤波器基础实验教学中的应用

肖 涵，李苑青

（哈尔滨工业大学〔深圳〕 实验与创新实践教育中心，广东 深圳 518055）

一、课程实验简介

“数字信号处理”课程是通信工程、电子科学、信息工程等专业的核心课程，具有知识点多、理论性强、应用性强特点，广泛应用在工程实践及科学研究中。数字滤波器设计是“数字信号处理”课程的一个重要内容，是图像处理、模式识别等后续课程的基础，国内外高校一般会在理论教学的同时，配置相应的实验内容，以加强学生对数字滤波器的理解与学以致用的能力。

数字滤波器的性能与滤波器的零极点分布密切相关，滤波器频响特性曲线的形态是所有极点和零点共同作用的结果。系统的极点分布多用于判断系统的因果性和稳定性，因果稳定的数字滤波器所有极点在单位圆内。系统的零点分布影响滤波器的相频特性，例如，因果稳定系统的所有零点都在单位圆内则为“最小相位系统”。在实际应用中，零极点分布图除可以用于判断系统因果性与稳定性外，与系统的其他性能（滤波器类型、通频带位置等）之间同样联系紧密。对于零极点的计算，若系统函数的分母、分子多项式阶数较高，手工计算极点与零点比较麻烦，可采用MATLAB中的求根函数roots来计算。在“数字信号处理”的实验部分，对于已知系统函数的数字滤波器，分析零极点分布主要用到MATLAB中的zplane函数。我校针对信号处理类实验，配备了虚拟仪器平台，通过在平台上直接输入数字滤波器系统函数分子分母的系数，可以直接得到零极点分布图。本文围绕零极点分布与滤波器类型、通频带特性，结合虚拟仪器平台与软件仿真，探讨零极点特性在数字滤波器基础实验中的应用。

二、极点与零点在滤波器实验的应用

根据滤波器结构是否存在反馈，数字滤波器可以分为FIR滤波器和IIR滤波器。FIR滤波器为非递归型滤波器，具有严格的线性相频特性且由于其单位脉冲响应为有限长度的，FIR滤波器为稳定的系统。IIR滤波器结构中存在反馈回路，其对于输入信号的响应是无限延续的，IIR滤波器可能是不稳定的。

（一）滤波器零点分布与阻带中心频率

N阶FIR滤波器的系统函数为：

FIR滤波器的极点在圆心处，在MATLAB仿真中利用zplane（B,1）来绘制FIR滤波器的零点分布，其中B为表示b的数值序列。图1为软件计算及虚拟仪器平台得到的3阶FIR滤波器零点分布，右图中显示了零点的极坐标及零点-圆心连线长度、与实轴正向夹角。

为了得到FIR滤波器的频率响应特性，一种方式是在MATLAB中直接计算，另一种方式是在虚拟仪器平台上搭建滤波器，将离散时间信号输入至滤波器来得到滤波器的频率特性。图2是学生在实验中实现的FIR滤波器，通过扫频法或逐点法得到滤波器的幅频响应。函数发生器产生模拟信号输入至采样保持器，采样时钟由数字输出模块提供，在一个采样脉冲时刻对模拟信号采样，信号幅度在下一个采样脉冲前处于稳定状态，采样保持器输出的离散时间信号进入滤波器。通过扫频或逐点测量，可以得到图1系数下滤波器的阻带中心频率。

图1 软件（左）与虚拟仪器平台（右）计算零点分布（b0=1，b1=-1.3，b2=0.902）

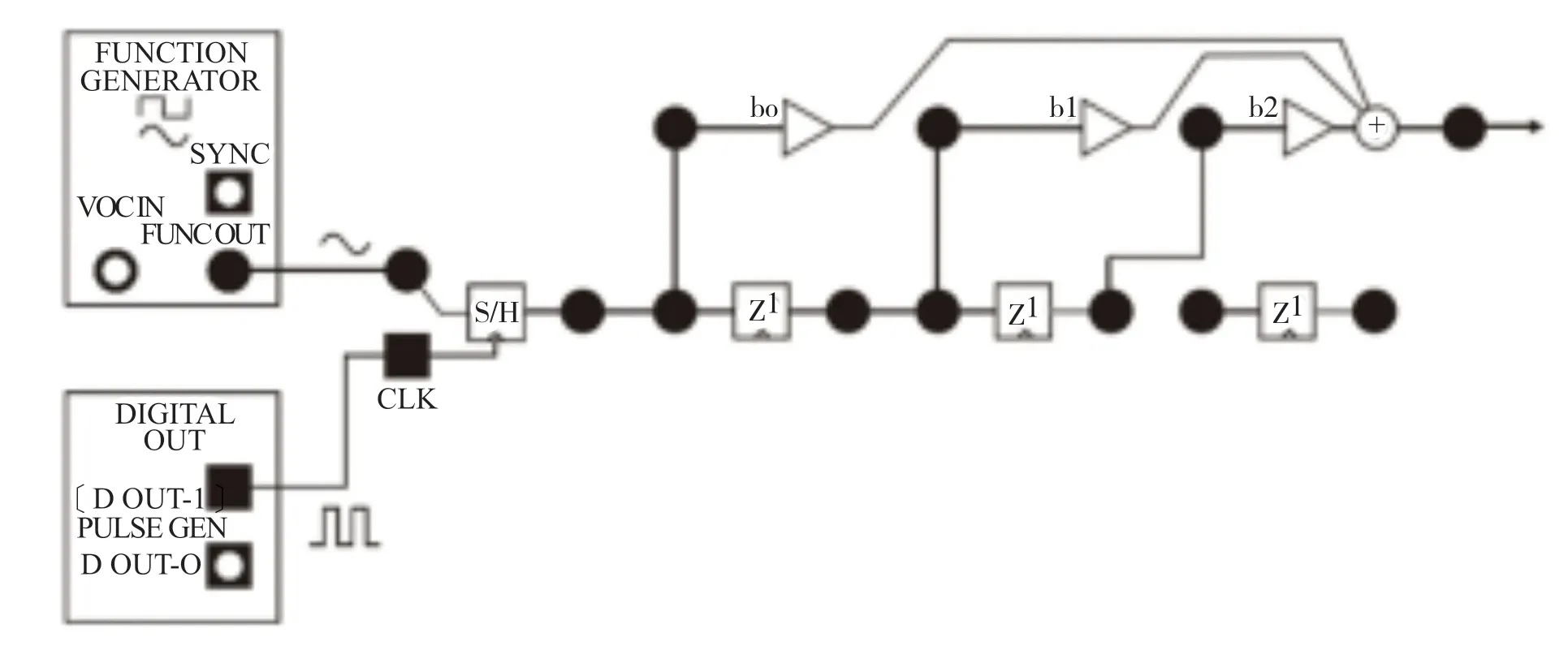
图2 虚拟仪器平台搭建的3阶FIR滤波器

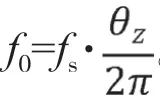
（二）滤波器零点分布与滤波器类型

N阶IIR滤波器的系统函数为：

其中在c和d分别为滤波器的零点与极点。采用几何方法研究IIR滤波器零点与极点分布对频率特性的影响，系统函数在单位圆内的极点处出现峰值、且极点越靠近单位圆，幅度特性的峰值越高越尖锐；系统函数在零点处出现谷值，且零点越靠近单位圆，谷值越接近零。因此，可以根据z平面上零点与极点的位置，对给定频率范围内滤波器的类型进行快速判断。

在数字滤波器基础实验的预习部分，学生通过IIR滤波器系统函数的分子多项式系数初步判断滤波器的类型，图3是实验中虚拟仪器平台计算的三种3阶滤波器的零极点分布图（绿色x为极点，红色○为零点）。三种滤波器的2阶极点均位于单位圆内，即滤波器系统稳定。其中（1）所示对应的滤波器的2阶零点位于z平面实轴-1位置处，由此判断（0，2）范围内滤波器类型为低通；（2）中滤波器的2阶零点位于z平面实轴1位置处，因此可以判断（0，2）范围内滤波器类型为高通；（3）中滤波器有两个1阶零点，分别位于z平面实轴-1位置与1位置处，由此判断滤波器在（0，2）范围内为高通滤波器。此外，若给出对模拟信号采样的频率，可估计滤波器的幅频响应。

图3 三种滤波器z平面的零极点图

（三）滤波器极点位置与峰值频率

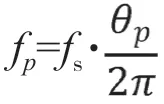
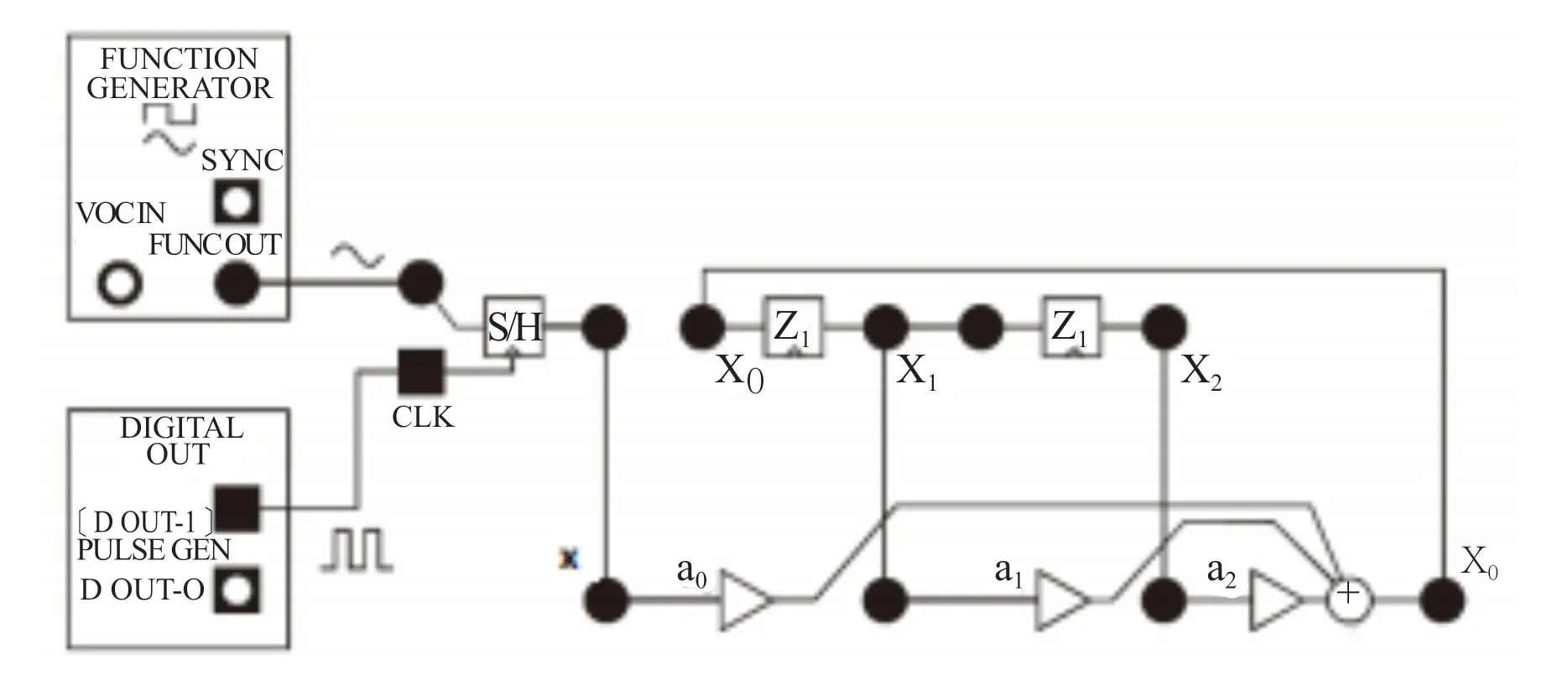
图4 虚拟仪器平台搭建的3阶IIR滤波器

三、采样频率与滤波器的特性

在实践应用中，对模拟信号进行数字处理的过程可能会涉及采样频率的改变，采样频率改变后滤波器的通阻带位置将发生偏移。为了在改变采样频率后保持数字滤波器的通频带位置不变，一种方式是重新设计滤波器，而另一种方式则是通过改变极点位置得到新的滤波器参数。数字滤波器的中心频率和阻带截止频率可通过软件仿真计算准确得到，而基于虚拟仪器平台搭建数字滤波器则有助于学生理解滤波器设计与实现过程中的实际问题。虚拟仪器平台搭建的数字滤波器，模拟信号经过采样保持器离散化后输入滤波器。若加倍采样频率，滤波器的中心频率将改变，理论上将极点相位调整为原相位的一半，可保持滤波器的中心频率不变。在实验过程中，利用虚拟仪器平台可求出零极点位置，但滤波器的中心频率可能需要微调才能达到设计参数指标。

需引起学生注意的是，如果只改变极点位置而系统函数分子多项式系数不变，由于采样信号的频谱与采样频率成正比关系，采样频率提高后滤波器幅频响应的峰值幅度将增大，考虑到虚拟仪器平台硬件条件的限制，在实验中信号可能由于内部节点饱和而造成滤波器输出信号信噪比降低，因此，在采样频率发生变化后除需关注输出端的幅频响应，还需关注滤波器的中间节点。综上，在设计数字滤波器时极点与单位圆的距离要适当，如果距离单位圆过近，滤波器系统具有非常高的增益，容易导致滤波器节点的信号发生饱和；而零点位于单位圆上，可使滤波器的幅频响应在阻带具有最大的衰减。

结语

本文从零极点特性出发，在数字滤波器基础实验中利用虚拟仪器平台及仿真软件绘制了零极点在z平面上的分布，分析了零极点分布对滤波器类型、通频带特性的影响，并探索了模拟信号离散化过程中采样频率对滤波器通频带位置及增益的影响。教学实践表明，通过本文所述实验内容，有助于学生对零极点特性与数字滤波器的设计形成直观的认识，进而强化学生对知识点的理解与应用。