基于四元数的地面光电探测系统指向标定

余东毅,柴云峰,宋 亚,樊芮锋,李丽亚

(华北光电技术研究所,北京 100015)

1 引 言

随着现代战争的发展,光电探测逐渐成为战争中获取信息重要技术途径,作为雷达探测的补充和辅助手段已经广泛应用于要地防护、防空反导等领域。地面光电探测系统对空中目标的精准定位,直接依赖于光电探测系统初始指向标定的精度高低。

目前地面光电探测设备常用具备自定位自定向功能的惯导设备进行定向标定,往往难以兼顾低成本、小型化与高精度的使用需求。同时地面光电探测设备在反无领域的应用和发展,进一步提高了低成本要求下的高精度定位方式,因此通过计算进行软件纠偏是高精度定位方式的必由之路。同时,现有的一些基于欧拉角的定位纠正算法存在死锁问题；基于七参数[1]的算法对近距离目标精度下降较快。

考虑到上述情况,本文对地面光电探测设备的初始标定方法进行了研究,建立了标定模型,求解了纠偏参数,给出了标定方案流程。最后基于本文给出的方案,对现有地面光电探测设备进行初始指向标定实验,并进行分析。

2 建立模型

对光电探测系统进行初步的指向标定是得到目标高精度经纬高信息的基础。即将基站光电系统光学指向的初始方位、俯仰角,与地理坐标水平面上的正北方向建立映射关系。由于光电探测设备中光学子系统各组分的光轴一致性误差、安装在机械框架上的轴系误差、设备安装时光学子系统和水平面之间的对准调平误差等一系列固定系统误差的存在[2-3],各基站光电系统在部署后,均需要高精度定位设备的辅助进行初始方位标定以消除这些固定偏差。而消除误差需由同一目标在不同坐标系下的测量值之间的对应转换关系给出。因而,建立如下的坐标系和坐标变换数学模型。

2.1 坐标系

光电探测设备光学系统指向坐标系(IRP):以光电探测设备成像组件中心处为原点,例如在红外探测设备中,原点即位于光学系统焦平面上的探测器芯片中心；光学系统红外设备在转台零位时主光轴指向为x轴正方向；二维图像的竖直方向为z轴正方向,依照右手关系建立坐标系。方位角为目标向量在xOy平面上的投影与x轴正方向夹角,逆时针为正；俯仰角度为目标向量与xOy平面的夹角；距离为目标距原点的直线距离。

光电探测设备大地坐标系(OEC):以光电探测设备转动中心位置为原点,即伺服转台方位、俯仰轴的交点；地理正北为x轴正方向；地理正西为y轴正方向；垂直xOy平面竖直向上为z轴正方向建立坐标系。特别的,在输出到终端时,方位角从逆时针为正且定义域为-π～π的弧度表示映射到顺时针为正且定义域为 0°～360°的角度表示,俯仰角从弧度表示改为角度表示。此坐标系即为光电探测系统转台设备编码器给出的方位、俯仰角度测量值所在的坐标系。

地理坐标系(LBH):LBH基本平面为大地参考椭球面。其中大地纬度B为通过赤道面与参考椭球面的法线的夹角,由赤道面为参考,法线垂直向北为正,向南为负；本初子午面向东为大地经度L；大地高H为位置点沿法线到参考椭球面。本文中,大地参考椭球面采用WGS-84标准,靶标的地理坐标也由高精度GPS定位测量设备给出其WGS-84坐标,并进行计算。

2.2 坐标系的旋转变换

光电探测设备的初始指向标定,即找到光学系统指向坐标系(IRP)与地理坐标系(LBH)之间的转换关系[4-5]。这种转换,包括从光学系统指向坐标系到光电探测设备大地坐标系的转换以及光电设备大地坐标系到地理坐标系的转换两部分。其中,光学系统指向坐标系到光电设备大地坐标系的偏差主要由设备安装时与大地不可避免的偏差角引起。严格来说,IRP系与OEC系的原点并不重合。对于一般的地面光电跟踪系统而言,IRP系与OEC系原点的误差在厘米量级,对主要工作区段10 km的同一点目标,最大误差不超过 arctan(10-6),约为0.001 mrad。考虑近距离1 km的同一点目标,最大误差不超过 arctan(10-5),约为0.01 mrad,小于光电探测设备光学成像系统的最小分辨角度,故此在坐标转换中不妨近似地认为两坐标系共原点。

因此上述坐标系之间的转换关系可以视为一种旋转,可以由欧拉角、旋转矩阵、四元数等数学工具进行具体描述。对于一般的旋转变换而言,这三种表示方法可以互相转化。但为了避免欧拉角描述下的万向节死锁问题,以及算法程序实现上的方便和计算机实时处理的性能,本文主要基于四元数的方法进行求解和计算[5]。

四元数是一种超复数[6]。作为用于描述现实空间的坐标表示方式,四元数q=a+bi+cj+dk,即为一实数与三个虚数单元的组合。其中,i2=j2=k2=ijk=-1。对于一三维空间的点在笛卡尔坐标系下有(x0,y0,z0),使用一个纯四元数p予以表示:x0i+y0j+z0k,简记为p(0,x0,y0,z0)。再创建一个单位四元数q(q0,q1,q2,q3),定义Rq(p)=qpq-1,得到Rq(p)也为一个纯四元数,因此视单位四元数q定义了一种由点p到点Rq(p)的旋转。

这一旋转的矩阵表示为:

(1)

这与旋转矩阵在形式上是一致的。

2.3 坐标系间转换

对光学系统指向偏差的修正,就是求解 IRP 系到 LBH 系的转换,其中具体涉及的坐标变换如下:

(1)各坐标系内的球坐标(r,θ,φ)与笛卡尔坐标(x,y,z)相互转换,具体转换关系如下:

(2)

(2)光学系统指向坐标系(IRP)内的(r0,θo,φ0)与光电探测设备大地坐标系(OEC)内(r1,θ1,φ1)的互相转换,由参数(Γ,Θ,Ψ,Δ)给出。该参数由测量值解出,其中由参数(Γ,Θ,Ψ)得到对应的四元数:

(3)

特别地,由于光电探测设备光学系统与伺服控制系统在安装上不可避免的误差,势必使整个光学系统指向坐标系在光电探测设备大地坐标系中存在一个较小的姿态角。对于指向偏差标定,方位角偏差带来的影响,在IRPxyz→OECxyz的坐标转换中被透明化。俯仰角偏差成为一个固定的误差,需要在坐标转换前后进行相应的考虑,由参数Δ给出。因此有:

(4)

及:

(5)

(3)光电探测设备直角坐标系(OECxyz)与地理坐标系(LBH)之间的转换,由基站光电设备的地理坐标(LO,BO,HO)在地心坐标系中的平移变换给出。具体的,将基站光电设备(LO,BO,HO)在地心直角坐标中表示得到:

(6)

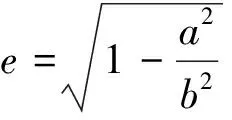
(7)

3 实验验证与误差

3.1 初始标定实验流程

在光电探测系统部署架设后,借助外部高精度卫星定位系统进行指向偏差标定。具体流程如下:

(1)通过高精度卫星定位系统得到设备当前部署位置的经纬高数据(L0,B0,H0)；

(2)在适当的距离和高度,通过携带高精度实时定位模块的无人机设备作为靶标,在至少三个点位得到具体的经纬高数据(Li,Bi,Hi),然后通过LBH→OECxyz变换,得到目标在基站光电设备坐标系中对应的(Xi,Yi,Zi)；

(3)对第i个靶标,控制基站光电设备的方位俯仰角度,使目标位于红外图像中心,并分别记录此刻由基站光电设备方位、俯仰角度编码器及激光测距机直接给出的目标位置坐标(ri,θi,φi)；

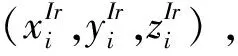
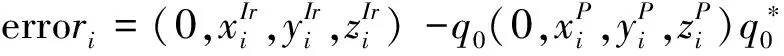
(6)以初值(αq,βq,γq,δ)=(0,90,0,Δθ)对(5)中的方程进行数值求解,解得相应参数,可以完全地建立上节中各坐标系间相应地变换关系,即在(IRP)与(LBH)间建立映射。

(7)将解得的修正角度(Γ,Θ,Ψ,Δ)代入显控软件中的纠正参数设置,可以得到实时纠正后的方位,对点目标测量得到误差并分析。

3.2 实验与结果

对于测距目标而言,距离越近一系列固定误差带来的角度偏差就越大[2]。本文选择携带高精度定位模块的大疆精灵4作为靶机,在1～2 km的距离内进行精度验证。

待标定设备位于Loc0,分别指向靶标Loci,i=1,2,3,…时得到对应的设备读数Aimi(ri,θi,φi),i=1,2,3,…特别地,对于不具备测距功能的待标定设备,可以简单地令ri=1。

由Loc0与Loci的经纬高坐标分别计算得到各目标指向的真实角度Reali(ri,θi,φi),i=1,2,3…将Aimi,Reali代入数值求解程序,得到纠偏参数(0.17564188,92.13168834,93.82522436,-0.4041),并写入设备控制程序。

放飞靶机实时获取高精度定位信息Loct,并与Loc0解出设备指向靶机的定位信息,与当前设备上报结果进行对比,结果如图1所示。

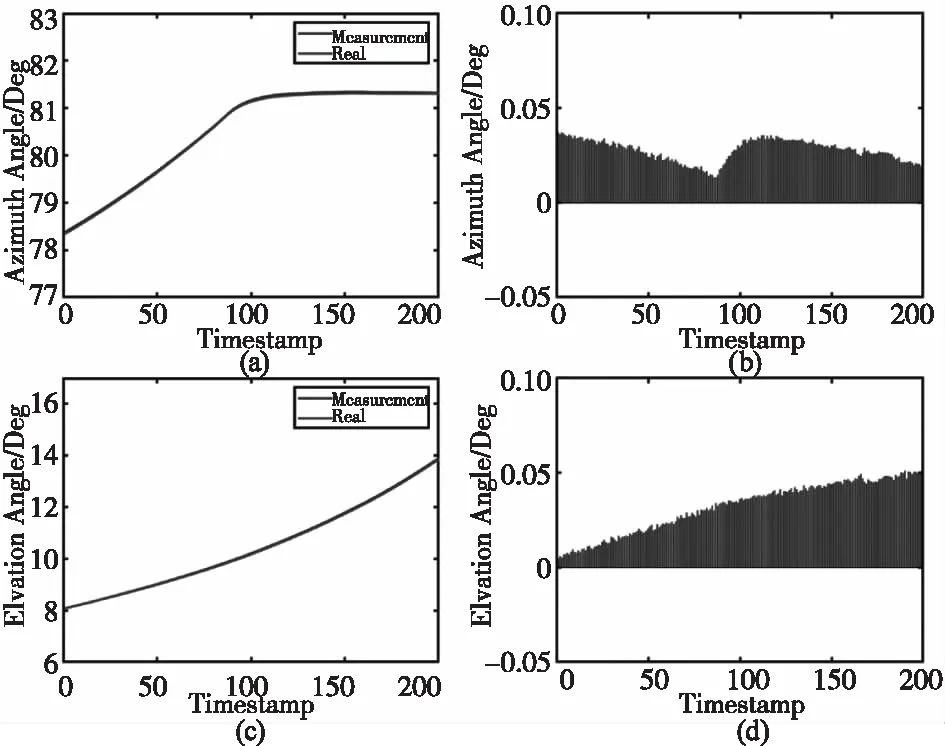
图1 靶机标定验证

图1(a)为目标方位角的真值与测量值的比较,图1(b)为目标俯仰角的真值与测量值的比较,图1(c)为目标方位角的测量误差,图1(d)为目标俯仰角的测量误差。得到方位角测量精度,即均方根误差ErrAzi=0.024°,俯仰角测量精度ErrEle=0.032°,均满足精度要求。靶机距标定设备直线距离1～2 km,如图2所示。

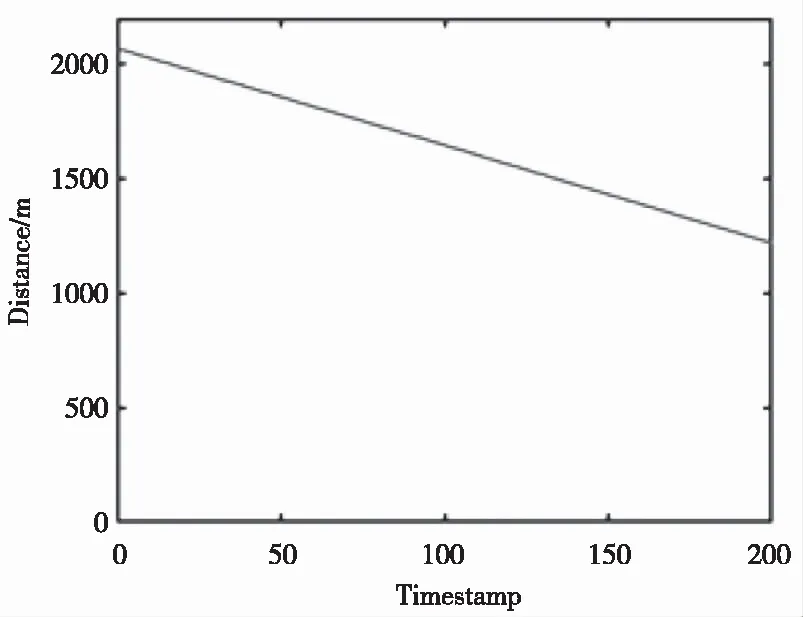
图2 靶机与探测设备距离

结合图1与图2,可以发现在靶机飞近标定设备的过程中误差逐渐增大,并在距设备1 km处俯仰角度偏差达到最大值。对于大于等于2 km的目标,俯仰角度显著低于0.05°,实现了高精度的指向标定。

3.3 误差分析

在光电探测系统的初始方位标定中,主要误差来源为以下几个方面[2]:

(1)光电探测系统在装配时,光学系统与伺服控制系统之间的固定偏差；

(2)可见光CCD、红外热像仪、激光测距机等光电载荷的光轴一致性误差；

(3)RTK、GPS等卫星定位系统对经纬高的测量误差；

(4)激光测距机的测距误差；

(5)光电探测系统工作的环境变化,如温度、湿度、气象等变化造成的误差；

(6)光电探测系统在对运动目标成像过程中的时延导致的跟踪、定位偏差。

其中,(1)、(2)的装配偏差可以通过质量管理进行一定程度的优化。且由于每次设备出厂安装后的装配偏差固定,可以通过多次实验对该固定偏差进行二次纠偏。(3)、(4)、(5)等随机误差在目标距离2 km以上30 km以下范围内影响较小,可以忽略。(6)中的时延偏差取决于设备具体的硬件状态与工作环境,也可以通过较为精准的标定实验进行一定程度上的消除与纠正,进一步提高目标定位精度。

4 结 论

本文提出的基于四元数的光电探测系统初始指向标定方法,具有较高的精度,对于大于等于2 km 的点目标,标定误差不超过 0.05°。对于地面光电探测系统的常见使用场景:

(1)雷达设备发现目标引导光电跟踪设备捕获目标；

(2)光电搜索设备发现目标引导光电跟踪设备捕获目标；

(3)光电搜索设备、光电跟踪设备引导小型激光对抗设备粗跟踪系统。

其中引导光电跟踪设备、小型激光对抗设备粗跟踪系统发现并捕获目标,仅需将目标引导至相应设备的红外/可见光成像视场可捕获范围内即可[7]。结合现有光学成像系统技术水平分析,此处最大允许偏差不小于0.2°[8]。本方法中标定误差0.05°,满足战术指标要求。

本方法标定流程简单,例如可使用搭载高精度定位模块的无人机作为靶标,选取多个采样点测量并计算得出(Γ,Θ,Ψ,Δ)四个参数即可完成标定。同时,本方法不需要额外集成定位定向设备,有助于具体工程实践大幅减少成本。本标定方法对地面光电探测系统,或其他类似系统的初始方位标定工作提供了参考,具有较大实用价值。