一类含有P-Laplacian算子的分数阶微分方程边值问题的多重正解
2022-09-24胡芳芳刘元彬
胡芳芳,刘元彬,张 永
(1.伊犁师范大学 数学与统计学院 应用数学研究所,新疆 伊宁 835000;2.新疆工程学院 数理学院,新疆 昌吉 830091)
0 引言
如今,分数阶微积分已被应用于许多领域,如工程、力学、物理、化学和生物学,特别是在科学和工程建模等相关领域[1-6],因此,分数阶微分方程和P-Laplacian算子微分方程引起了数学家们的广泛关注,对分数阶微积分的各种问题进行了大量的专题研究[7-13].
在文献[14]中研究了如下边值问题
(1)
在文献[15]中考虑了以下问题
(2)

基于上述研究,本文利用P-Laplacian算子分析了以下分数阶微分方程边值问题:
(3)
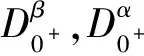
1 预备知识
在这里,给出一些定义、预备引理及格林函数的一些性质,这些预备知识在后面会用到.
定义1[16]连续函数y:(0,+∞)→R的α>0阶Riemann-Liouville积分定义为
其中等式右端在(0,+∞)内有定义.
定义2[16]连续函数y:(0,+∞)→R的α>0阶Riemann-Liouville微分定义为
其中n是大于或等于α的最小整数.

u(t)=c1tα-1+c2tα-2+…+cntα-n,
ci∈R,i=1,2,…,n,
其中n是不小于α的最小整数.

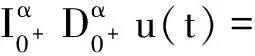
其中n是不小于α的最小整数.
引理3设y∈[0,1],1<β≤2,3<α≤4,则分数阶微分方程边值问题
(4)
有唯一解

(5)
其中:
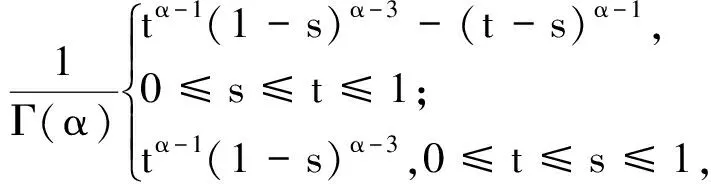
(6)

(7)

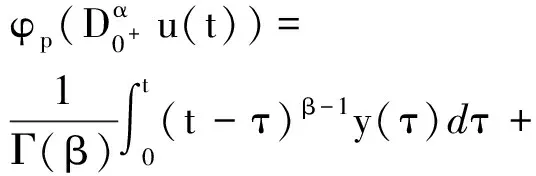
(8)
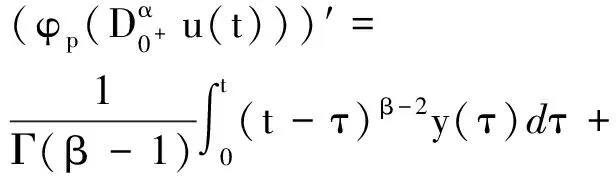

将c1,c2代入式(8),可得
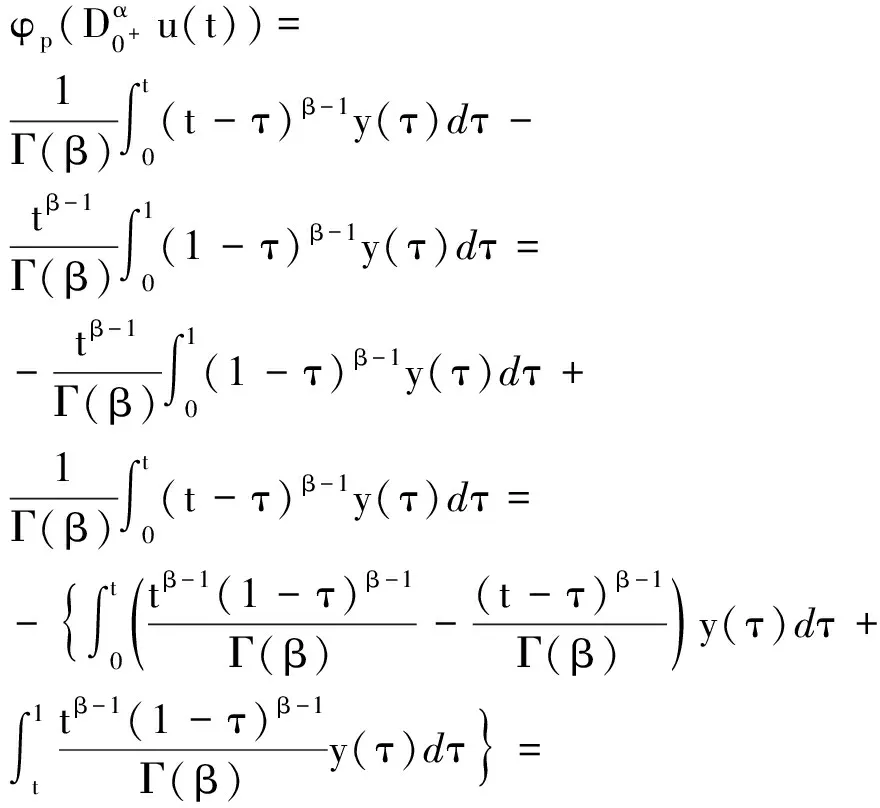

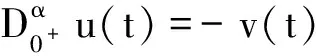

(9)
由边值条件u(0)=u′(0)=u″(0)=u″(1)=0,可得
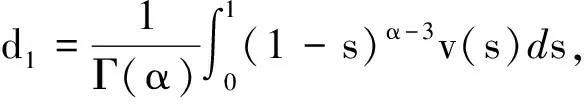
将d1,d2,d3,d4代入式(9),可得
引理4函数G(t,s),H(t,s)满足如下性质:
(1)对任意的t,s∈[0,1],
G(t,s)≥0,H(t,s)≥0;
(10)
(2)对任意的t,s∈[0,1],
G(t,s)≤G(1,s),H(t,s)≤H(s,s);
(11)
(3)存在两个正函数k(s),q(s)∈C[0,1],满足

(12)

(13)
证明(1)由函数G(t,s),H(t,s)的表达式可知式(10)显然成立.
(2)当0≤s≤t≤1时,有

当0≤t≤s≤1时,有
则函数G(t,s)在s∈[0,1]上关于t单调递增.
由引理4的(1)及函数G(t,s)的单调性可知
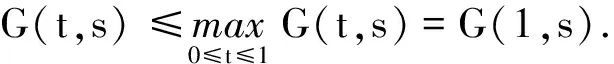
下面研究函数H(t,s)的性质.
当0≤s≤t≤1时,有

则函数H(t,s)是关于t单调递减的,即H(t,s)≤H(s,s).
当0≤t≤s≤1时,有
则函数H(t,s)是关于t单调递增的,即H(t,s)≤H(s,s).则式(11)成立.
(3)由函数G(t,s)的单调性,令
则有
其中
由函数G(t,s)的单调性,有
故可取
则式(12)成立.
再由函数H(t,s)的单调性,令
则有
其中
再由函数H(t,s)的单调性,有
故可取

则式(13)成立.
特别的,如果α=2,则r=0.5;α→1时有r→0.75.
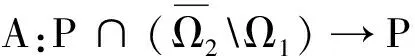
(1)‖Ax‖≤‖x‖,x∈P∩∂Ω1,‖Ax‖≥‖x‖,x∈P∩∂Ω2.
(2)‖Ax‖≥‖x‖,x∈P∩∂Ω1,‖Ax‖≤‖x‖,x∈P∩∂Ω2


(C1){x∈P(θ,b,d)|θ(x)>b}≠φ且对x∈P(θ,b,d),有θ(Ax)>b;

(C3)当x∈P(θ,b,c)且‖Ax‖>d时,θ(Ax)>b.
那么A至少有三个不动点x1,x2,x3,满足
‖x1‖ ‖x3‖>a,θ(x3) 定理1T:P→P是全连续算子. 所有T(Ω)是一致有界的. 另外,由于G(t,s)在[0,1]×[0,1]上是一致连续的,因此对固定的s∈[0,1]及任意的ε>0,存在δ>0,使得当t1,t2∈[0,1],t1 |G(t2,s)-G(t1,s)|< 于是 即T(Ω)是等度连续的.由Arzela-Ascoli定理可知,T:P→P是全连续的. 记 定理2假设f(t,u(t))为C[0,1]×[0,∞)上的连续函数,若存在两个正常数r2>r1>0,使得 (H2)当(t,u(t))∈[0,1]×[0,r2]时,f(t,u(t))≤(Mr2)p-1, 则边值问题(3)至少有一个正解u,使得r1<‖u‖ 证明令Ω1={u∈P|‖u‖ 因而‖Tu‖≥‖u‖,u∈∂Ω1. 令Ω2={u∈P|‖u‖ 因而‖Tu‖≤‖u‖,u∈∂Ω2. 由引理5可知,算子T至少有一个不动点u,即边值问题(3)至少有一个正解且满足r1<‖u‖ 定理3假设f(t,u(t))为C[0,1]×[0,∞)上的连续函数,若存在正常数且满足0 (A1)当(t,u(t))∈[0,1]×[0,a]时,f(t,u(t))≤(Ma)p-1; (A3)当(t,u(t))∈[0,1]×[0,c]时,f(t,u(t))≤(Mc)p-1, 则边值问题(3)至少有三个正解u1,u2,u3,且满足 {u∈P(θ,b,c)|θ(u)>b}≠φ. 即对任意的u∈P(θ,b.c),θ(Tu)>b.所以引理6中的条件(C1)成立. 综上所述,引理6的所有条件都满足,根据引理6,可以得出边值问题(3)存在三个正解u1,u2和u3,满足 例1考虑边值问题 通过计算得M≈19.69,N≈2846.37,选择r1=0.001,r2=0.9,有 根据定理1,例1可以得到一个解u,使得0.001≤‖u‖≤0.9. 例2考虑边值问题 其中 根据定理3,例2可以得到三个正解u1,u2,u3,且满足 本文以分数阶微分方程理论为基础,首先给出相应格林函数及其性质,其次将边值问题转化为与其等价的积分方程,最后结合锥压缩锥拉伸不动点定理和Leggett -Williams不动点定理,获得了边值问题(3)一个及多个正解的存在性,并给出实例加以验证.2 结果与讨论






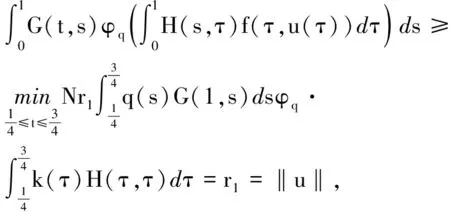

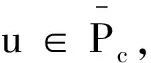
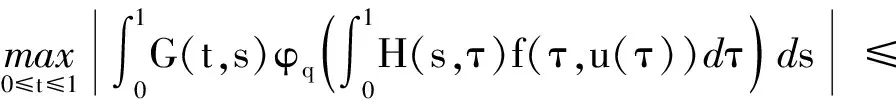

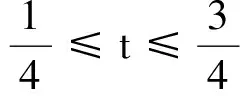
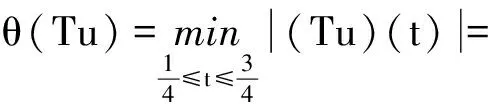
3 例子

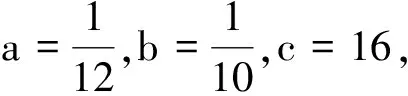
4 结语
