Configurational entropy-induced phase transition in spinel LiMn2O4
2022-09-24WeiHu胡伟WenWeiLuo罗文崴MuShengWu吴木生BoXu徐波andChuYingOuyang欧阳楚英
Wei Hu(胡伟) Wen-Wei Luo(罗文崴) Mu-Sheng Wu(吴木生)Bo Xu(徐波) and Chu-Ying Ouyang(欧阳楚英)
1Department of Physics,Laboratory of Computational Materials Physics,Jiangxi Normal University,Nanchang 330022,China
2School of Ecology and Environment,Yuzhang Normal University,Nanchang 330103,China
Keywords: configurational entropy,LiMn2O4,phase transition,Jahn-Teller distortion
1. Introduction
Lithium-ion batteries (LIBs) have been widely used in many fields due to their excellent electrochemical performances, such as potable electronic devices, electric vehicles,and smart grid storage over the last few decades.[1-4]The performances of LIBs,i.e., energy density, capacity, rate capability, and cycling life, are closely related to the cathode materials. The spinel-type compound, LiMn2O4, is considered as one of the most promising materials with good electrochemical performance in LIBs due to its good thermal stability and safety, low cost, environmental benign, high energy density,etc.[5-8]At ambient temperature, the crystal structure of LiMn2O4belongs to the cubicFd¯3mspace group,[9]
where lithium ions are located at the tetrahedral 8asites,manganese ions at the octahedral 16dsites and oxygen ions at the 32esites.[10]Since the average valence of manganese ions in LiMn2O4is 3.5, the same numbers of Mn3+and Mn4+ions are randomly distributed at the 16dsites. However, upon cooling a first-order phase transition occurs at a temperature of ca 280 K from cubic to tetragonal(I41/amd) phase,[11-16]which hinders this compound from being put into practical application. Yamada and Tanaka[11]observed the splitting of reflections at low temperature by using thermal analysis and powder x-ray diffraction. This indicates that LiMn2O4undergoes phase transition at low temperature. Yamaguchiet al.[15]investigated an x-ray absorption fine structure (XAFS)of LiMn2O4, further confirmed the fact of the phase transition at low temperature, and reported that a phase transition occurs in the vicinity of 280 K by differential scanning calorimetric (DSC) measurement. Piszoraet al.[17]found that this phase transition is related to the Jahn-Teller effect and partial charge ordering of Mn3+and Mn4+ions,but the detailed mechanism has not been reported. The potential profile test of LiMn2O4by Abikoet al.[18]found that LiMn2O4has an additional low voltage plateau and spinel powder is pulverized by lattice stress at low temperatures. Chung and Kim[19,20]reported that the presence of the tetragonal phase of LiMn2O4particle due to a Jahn-Teller effect is one of the reasons for capacity fade by usingin situlaser probe beam deflection technique. Therefore, in order to avoid the performance degradation caused by low temperature phase transition and promote the wide application of LiMn2O4cathode, it has become an urgent topic to study phase transition mechanism of LiMn2O4at the low temperature.
As is well known,Jahn-Teller(JT)distortion exists in the MnO6octahedron for Mn3+ions,but not for Mn4+ions. Generally speaking,the JT distortion gives rise to the lowering of the symmetry and the observed cubic phase at room temperatures seems not reasonable,as the MnO6framework is tetragonally distorted. Considering the randomly distributed Mn3+ions in the lattice,it is also possible that the orientation of the JT distortion is random,namely,the elongation of the Mn3+O6octahedron is randomly distributed along thex-,y-,andz-axis directions. That is to say, the configuration of LiMn2O4may be related to the distribution of Mn3+ions and the elongation direction of the Mn3+O6octahedron. In this way, the cubic structures can also be exit due to the JT effect of the Mn3+O6octahedron. Furthermore, Piszora[17]reported that the phase transition is induced by the JT distortion and partial charge ordering of Mn3+and Mn4+ions with temperature decreasing,indicated by using powder synchrotron radiation diffraction.On the basis of this analysis, we speculate that the structural phase transition from cubic to tetragonal phase is closely related to the configurational entropy originating from the distribution of the Mn3+and Mn4+ions and the orientation of the JT distortion direction of Mn3+O6octahedron.
To further verify and understand the mechanism of phase transition, we study the transition between cubic phase and tetragonal phase by including the configurational entropy contribution to the Gibbs free energy from the thermodynamic point of view in this work.The ground state energy is obtained by using the first-principles calculations. It is shown that the average ground state energy of the cubic LiMn2O4(disordered phase)is higher than that of the tetragonal one(more ordered phase)at a temperature of 0 K.When the configurational entropy is included, the Gibbs free energy of the cubic phase lowers with the temperature increasing and finally the phase transition from cubic phase to tetragonal phase happens at a temperature of 267.8 K, which is close to the experimental result.[11,15,18]
2. Computational method
To optimize the structures and obtain the ground state energy values of different structures and phases, we performed density functional theory (DFT) calculations by using the Viennaab-initiosimulation package (VASP).[21-23]The method of the projected augmented wave (PAW)[24,25]pseudopotentials was used to describe the ion-electron interactions. The electron exchange and correlation functional were treated within the spin polarized generalized gradient approximation(GGA)in the form of the Perdew-Burke-Ernzerh(PBE)functional.[26]A cutoff energy of 500 eV was selected for the plane wave basis set. In order to account for the strong onsite Coulomb repulsion of Mn-3d electrons, the GGA+Umethod[27,28]was adopted,which could accurately predict the electronic structures of transition metal complexes. Based on previous reports,the effectiveUvalue for d-orbital of Mn ions was set to be 4.5 eV.[29,30]The Monkhorst-Pack scheme[31]with 3×3×3k-points sampling mesh was used for the integration in the irreducible Brillouin zone. The atomic positions and the lattice parameters were fully relaxed, and the final force was less than 0.01 eV/˚A for each atom. The calculation workflow was managed by the high-throughput computational platform for battery materials.[1]
3. Results and discussion
The spinel-type LiMn2O4consists of 32 O,16 Mn,and 8 Li atoms in a conventional unit cell as shown in Fig. 1. According to the crystal field theory, the Mn-3d orbital will undergo an energy level splitting,producing a double degenerateeg(dx2-y2,dz2)and a triple degeneratet2g(dxy,dyz,dxz)orbitals under an octahedral crystal field as shown in Fig.2.

Fig.1.Ball and stick models of(a)cubic and(b)tetragonal LiMn2O4,along with lattice parameters(in units of ˚A).Comparing with cubic phase,the lattice c of tetragonal phase expands,while lattices a and b shrink. Arrows in the inset indicate the Jahn-Teller distortion direction of Mn3+ions.The red,green,and blue spheres represent O,Li,and Mn atoms,respectively.

Fig.2. Schematic diagram of energy level splitting for Mn-3d orbital under an octahedral field.
The projected density of states and corresponding electronic configuration of the Mn3+ion and Mn4+ion in the LiMn2O4are shown in Fig.3. As can be seen, the electronic configuration of the Mn-3d state of the Mn3+ion and Mn4+ion aret32ge1gandt32ge0g, respectively.[32,33]Since theegorbital is directly facing the ligand atom,it is subjected to larger Coulomb repulsion,resulting in the JT distortion of Mn3+ion in MnO6octahedron,forming four short and two long Mn-O bonds in the Mn3+O6octahedron as shown in Table 1. For Mn4+ions, theegorbital is not occupied by electrons, so the bond lengths in the Mn4+O6octahedron are approximately equal. Considering the equivalence of thex,y, andzdirections, the orientation of the JT distortion can be in any direction. If the orientation is randomly distributed along thex,y,andzdirections, the crystal structure behaves as cubic phase.In contrast, if the orientation of the JT distortion is unique in one direction,say,along thezdirection,the lattice constantcwill be larger than that ofaandband thus the crystal structure acts as tetragonal phase. Experimentally, Chung and Kim[19]also observed that the latticecexpands and the lattice a shrinks during the phase transition from cubic to tetragonal phase for LiMn2O4. In order to study the phase transition, we need to construct and simplify these two models.

Fig.3. Projected densities of states and corresponding electronic configurations of Mn-3d orbitals for(a)Mn4+and(b)Mn3+in LiMn2O4,with Fermi levels set to be 0 eV.

Table 1. The Mn-O bond length in MnO6 octahedron, where longbonds are highlighted.
As mentioned above,there are 16 Mn ions in the unit cell of the spinel LiMn2O4. Among them, half of these Mn ions are trivalent Mn ions, and the others are tetravalent ones. On the other hand, the JT effects of Mn3+ions have three possible distortion directions(x,y,andzdirections). Therefore,the total number of possible Mn3+distributions and Mn3+O6orientation configurations in the unit cell of LiMn2O4isC816×38.For each configuration,the ground state energy of the unit cell can be different,and in this work we use an average over several typical models we employed, which will greatly reduce the happenchance of a single configuration. Owing to the vast number of possible configurations and our limited computational resource,we select only 12 configurations(as shown in Fig. 4) to optimize their structures and calculate the ground state energy. The optimized lattice parameters and the corresponding energy values for the selected 12 configurations are listed in Table 2. The average values of the lattice parameters and the ground state energy values of the cubic phase are also listed in Table 3,which are considered to be the lattice parameters and ground state energy of the cubic phase in this work.Likewise, the LiMn2O4in the tetragonal phase is also dealt with by this procedure. Owing to the sole direction of the JT distortion(zaxis in our calculations)for the tetragonal phase,the degree of freedom of the JT distortion is not considered.

Fig. 4. Jahn-Teller distortion directions of the eight Mn3+O6 for the selected 12 cubic configurations, with horizontal, vertical, and slanted arrows representing the directions along the x,z,and y axes,respectively.

Table 2. Lattice parameters and total energy values of selected 12 cubic configurations.

Table 3. Lattice parameters and average ground state energy values of LiMn2O4 unit cell in cubic and tetragonal phases. Herein, the lattice parameters and total energy values are average values of various configurations calculated.
Therefore, only the configurations with the different Mn3+distributions are considered. Here, three different configurations are used to calculate the average values of lattice parameters and the ground state energy values as listed in Table 3. Likewise,these average values are taken as the average values of the lattice parameters and ground state energy values of the tetragonal phase in this work.
As is well known, the Gibbs free energyGcan be expressed asG=H-TS, whereHdenotes the enthalpy, andSis the entropy. For solid phase, the contribution of pressure toHcan be ignored. As a result, the change of the Gibbs free energy is influenced by the environment through the entropy. Therefore, only the configurational entropy is taken into account in this work. After the ground state energy is obtained,we need to determine the configurational entropy(Sconf),which is given asSconf=kBlnΩ,whereΩis the number of configurations,kBrepresents the Boltzmann constant. Herein, it should be pointed out that the interaction between Mn ions is ignored. Therefore, for the cubic phase,Ω=C816·38,whereas for the tetragonal phase,Ω=C816. The Gibbs free energy as a function of temperature for the cubic phase and tetragonal phase are shown in Fig. 5. As can be seen, a crossover point at a temperature of 267.8 K can be found. When the temperature is higher than 267.8 K,the cubic phase is more stable than the tetragonal one. When the temperature decreases below 267.8 K,the transition from cubic phase to tetragonal phase is expected. This theoretically predicted phase transition temperature of about 267.8 K for LiMn2O4from cubic to tetragonal phase is close to that observed experimentally (~280 K) by using x-ray absorption spectroscopy by Yamada and Tanaka,[11]Yamaguchiet al.,[15]and Abikoet al.[18]This also shows the important role of configurational entropy in the phase transition process.
Although the phase transition temperature obtained from our calculations is close to that from experiments, there are still some factors that we did not consider in this study.Firstly,the vibrational entropy induced by the finite temperature is not included in our model. This cannot be an important fact, for the difference in vibrational entropy between the cubic phase and tetragonal phase should be small and the bonding interactions are the same in the compound. Secondly, it is worth noting that the limited configurations chosen in our calculations also influences the accuracy of the ground state energy.Despite these, we believe that the introduction of configurational entropy can qualitatively reveal the nature of transition between cubic phase and tetragonal phase, which is helpful for us to understand the phase transition of the spinel-type LiMn2O4.
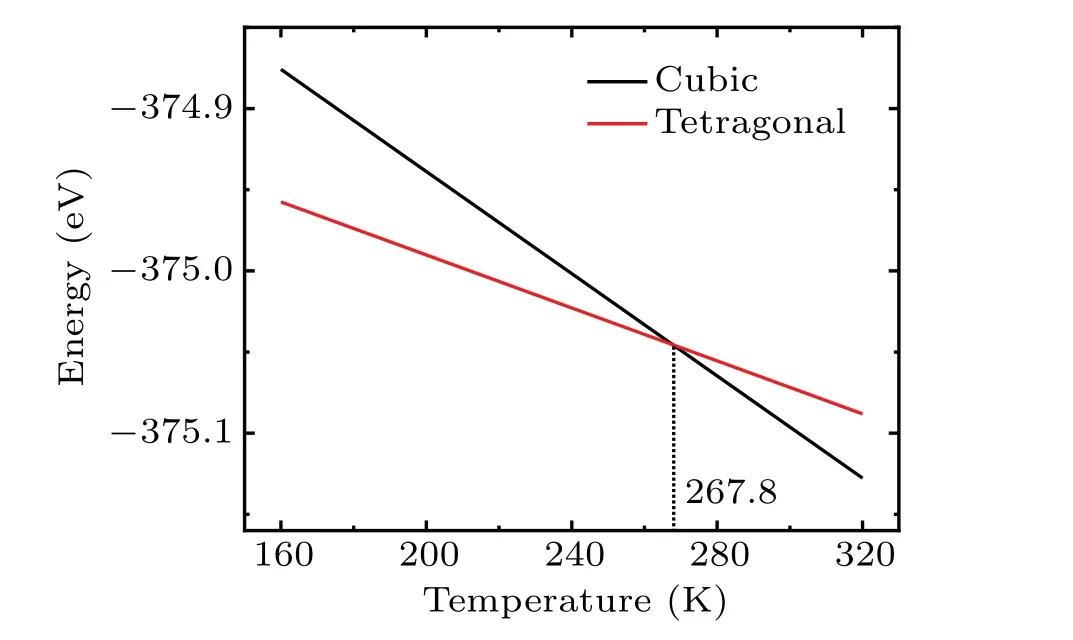
Fig.5. Plot of Gibbs free energy versus temperature of LiMn2O4 unit cell for cubic phase and tetragonal phase. Herein,the ground state energy employed is average value of the corresponding configuration as shown in Table 3.
4. Conclusions
In this work, the phase transition of the spinel LiMn2O4between cubic phase and tetragonal phase are studied through DFT calculations combined with thermodynamic analysis.The ground state energy is calculated through DFT for each configuration at zero temperature, while the entropy is evaluated through atomic configurational evaluation. It is found that the ground state energy of the cubic phase with the disordered JT distortion direction of the Mn3+ion is higher than that of the tetragonal phase with the ordered orientation of the JT distortion. On the other hand, the configurational entropy of the cubic phase is higher than that of the tetragonal phase.As a result,the cubic phase is more stable at high temperatures while the tetragonal phase is more stable at relatively low temperature. The phase transition temperature is evaluated to be 267.8 K through combining the calculated total ground state energy with the configurational entropy,which is comparable to the experimental value. These findings help further understand the phase transition of LiMn2O4at low temperature,and serve as a complement to experimental studies. In particular,the failure of LiMn2O4cathode is more clearly recognized at low temperature,which helps broaden the application scope of LiMn2O4.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant Nos.12174162,51962010,12064015,and 12064014).
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Erratum to“Accurate determination of film thickness by low-angle x-ray reflection”
- Anionic redox reaction mechanism in Na-ion batteries
- X-ray phase-sensitive microscope imaging with a grating interferometer: Theory and simulation
- Regulation of the intermittent release of giant unilamellar vesicles under osmotic pressure
- Bioinspired tactile perception platform with information encryption function
- Quantum oscillations in a hexagonal boron nitride-supported single crystalline InSb nanosheet
