Coherent Controlling Single Photon Asymmetric Transmission in the Atom Chirally Coupled Waveguide System∗
2019-11-07WeiHu胡伟XiaoSanMa马小三BingWang王兵XianShanHuang黄仙山andMuTianCheng程木田
Wei Hu (胡伟), Xiao-San Ma (马小三), Bing Wang (王兵), Xian-Shan Huang (黄仙山), and Mu-Tian Cheng (程木田)
1School of Electrical Engineering and Information, Anhui University of Technology, Maanshan 243002, China
2Anhui Provincial Key Laboratory of Power Electronics and Motion Control, Anhui University of Technology, Maanshan 243002, China
3School of Mathematics and Physics, Anhui University of Technology, Maanshan 243002, China
Abstract We theoretically investigate the influences of two coherent driving fields on the asymmetric transmission of single photon in the atom-waveguide system.The atom is considered as a Λ system.One transition of the atom chirally couples to the waveguide.The other transition is driven by two coherent driving fields.The transmission probabilities for the single photon incidents from the left (Tlr) and right (Trl) are given respectively.The calculated results show that one can realize Tlr=0 (Trl≠ 0) or Trl=0 (Tlr≠ 0) by manipulating the phase difference between the two coherent driving fields.The influence of the decay rate of the metastable state on the asymmetric transmission is also discussed.
Key words:single photon diode, waveguide, chiral coupling
1 Introduction
Single photon diode, which allows the transmission of single photon in only one direction, has important applications in quantum information processing.The realization of single photon diode has been discussed widely in recent years.[1−9]Hafezi and Rabl suggested using an optomechanical resonator to break the parity-time symmetry to realize the nonreciprocal of the single photon transport properties.[1]Later, Xiaet al.proposed to realize single photon isolator in the atom-whispering gallery microresonator-waveguide system.[2]Their idea was demonstrated by Scheucheret al.[9]In the atomic system, there are also a lot of advancements in realization of optical diode.For example, Wanget al.reported optical diode based on a moving photonic crystal and experimentally demonstrated in a room temperature Cs vapor cell.[10]Xia, Xu, and Yang proposed optical diode on fewphoton level based on asymmetric cavity configuration,[11]which is experimentally demonstrated very recently.[12]
Atom-waveguide system with chiral coupling is a good platform to investigate the non-reciprocal quantum phenomena.[13]The chiral coupling between atom (artificial atom) and waveguide has been realized in many configurations, such as atom-nanofiber system,[5,14]quantum dot-nanobeam waveguide system,[15]and quantum dotphotonic crystal waveguide system.[16−17]Here, the chiral coupling means that the coupling strengths between the atom and photon in the waveguide are propagationdirection dependent.Many quantum devices, such as single photon router,[18−23]frequency converter,[24]gate,[25]SWAP gate,[26−27]quantum interface between atom and photon,have been proposed.[15]The single photon diode has also been discussed in such a system.The main idea is that when the single photon incidents from one direction of the waveguide,it is scatted into free space such that there is no transmission in the other end.However, when the photon incidents from the other direction of the waveguide, it can pass through freely due to no interaction between the atom and waveguide.Thus, asymmetric transmission is realized.For the two-level system chiral coupling to the waveguide,the diode can be realized only for the resonant photon.[5]However, one can use an external coherent field to drive Λ-type system to realize single photon diode with specific frequency points.[28]
Phase difference between two coherent fields can play important roles in manipulating dynamics of quantum systems, such as narrowing down the atomic spectrum of spontaneous emission,[29]controlling the dynamical behaviors of nonclassical correlations,[30]and population swapping.[31]Recently, Yuan and Fan proposed to realize nonreciprocal single photon transmission by using phase difference between two coherent fields in the system composed of waveguide coupling to a pair ofV-type systems.[32]Yuet al.proposed phase difference controlled single photon switching in the atom-cavity-waveguide system and waveguide-multiple Λ-type system.[33−35]In this paper, we further investigate theoretically manipulation single photon propagation properties in atom-waveguide chiral coupling system by phase difference between two coherent fields.We show that,the asymmetrical degree of the transmission can vary between 0 and 1 by controlling the phase difference.Our results may find applications in designing all-optical quantum devices at single-photon level.
2 Model and Method
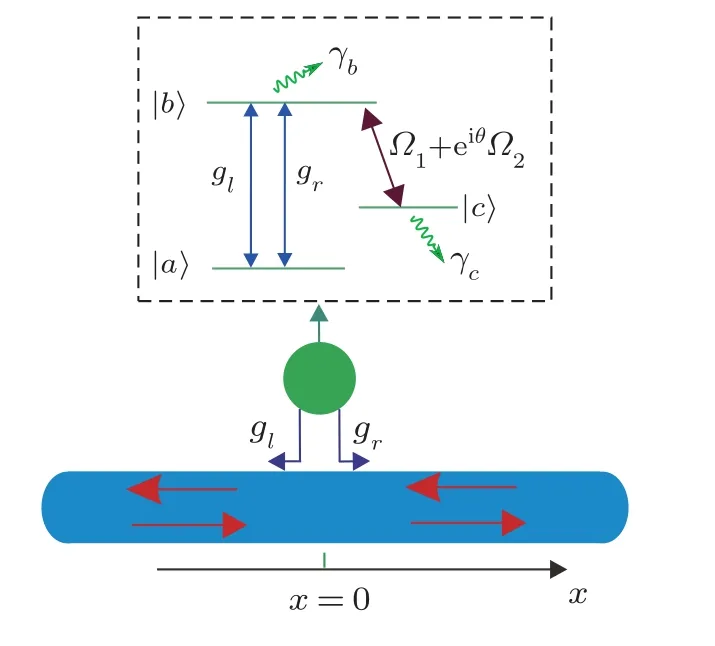
Fig.1 (Color online) The system considered in the manuscript.Λ system interacting with a one-dimensional waveguide.The transition between |a〉and |b〉chiral couples to the waveguide.The transition between |b〉and |c〉is resonantly driven by two coherent fields.The phase difference between the two coherent fields is θ.
The system we consider in this study is shown in Fig.1.An atom with three energy levels chirally couples to the waveguide.The transition between states|a〉 and|b〉 couples to the waveguide.The coupling strength between the transition |a〉⇔|b〉 and the right (left) propagating photon in the waveguide isgr(gl).The transition between the states |b〉and |c〉is decoupled from the waveguide.Instead, it is resonantly driven by two coherent fields.The equivalent Rabi frequency of the two coherent fields can be expressed as
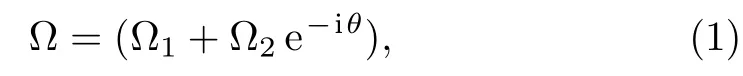
where Ω1and Ω2are the Rabi frequencies of each of the coherent fields.θis the phase difference between the two fields, which can be controlled by the time delay between the two fields.[31]In this study,we will discuss how to control the single photon asymmetrical transmission properties by modulating the phase differenceθ.
The Hamiltonian describing the system is given by(=1)[36−37]
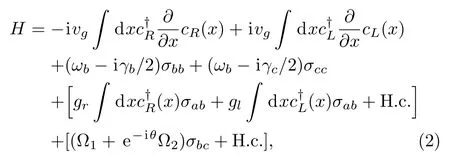
where(x) denotes creating a right/left propagation photon atxin the waveguide.vgis the velocity of the propagation photon.ωbis the frequency of energy level |b〉.Here,we have set the energy level |a〉as the reference.γb(γc) denotes the energy loss rate ofSince the coupling is chiral,gr≠gl.Whengr=gl, the coupling is non-chiral.σmn(m,n=a,b,c) is the dipole transition operator.
Since we only consider the single photon diode, the wavefunction can be expressed as
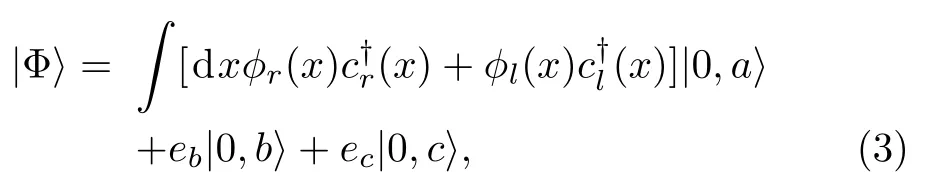
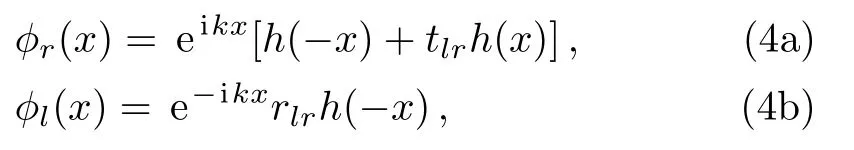
wherek=ω/vg.h(x) is the step function withh(0)=1/2.tlrandrlrrespectively denote the transmission and reflection amplitudes for the single photon incident from the left of the waveguide.From Schrödinger equationafter some calculations, one can obtain
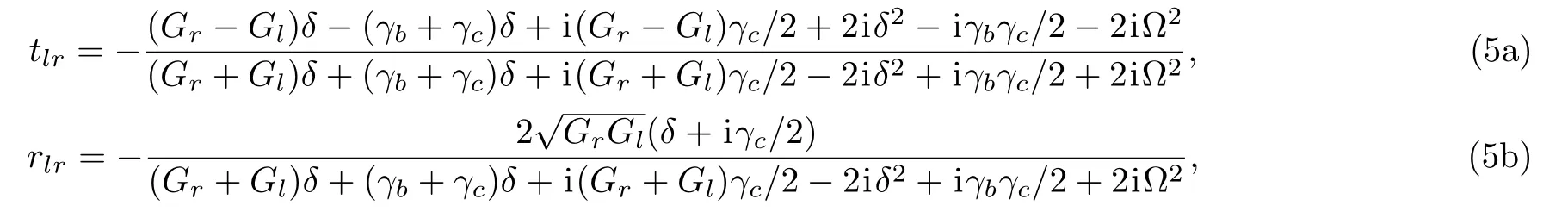
3 Results and Discussions
In this section, we show how to control single photon routing by manipulating the phase differenceθ.
3.1 Ideal Case with Gl=0, γc=0
Firstly, we discuss the phase controlled single photon routing for the ideal case.WhenGl=0,γc=0 are satisfied, Eqs.(5a), (5b) degenerate into
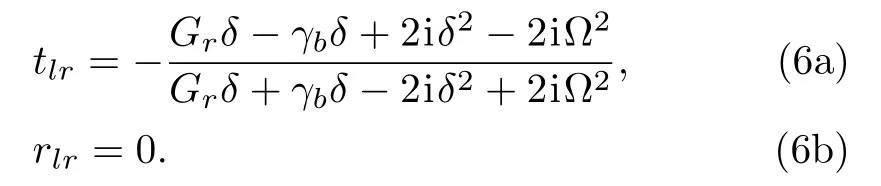
If there is no driving fields Ω1or Ω2, the system degenerates into a two-level system.One can obtain that whenGr=γbandω=ωb,tlr=rlr=0.It means that the photon with energyω=ωbwill be scattered into the free space when it incidents from the left of the waveguide.Thus,the transmission probability is zero.However,when the photon incidents from the right of the waveguide, it will not interact with the atom due toGl=0.It can be transmitted with probability of 1.Thus a diode is realized.
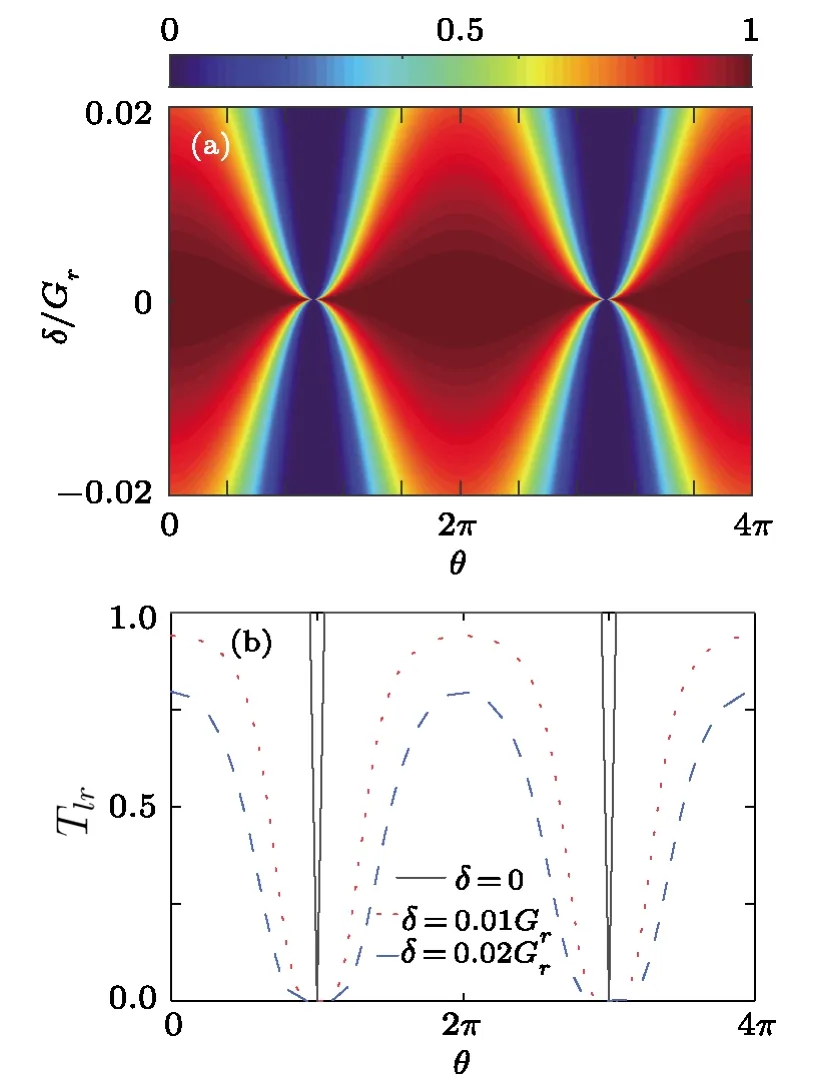
Fig.2 (Color online)Phase difference controlled Tlr.(a)Tlr as functions of δ, and θ.(b) is cut from (a) at δ=0,0.01Gr and 0.02Gr, respectively.In the calculations, γb=Gr,Gl=0,γc=0,Ω0=0.1Gr.
When the driving fields are applied, one can obtain that whenω=ωTlr=0=ωb ± |Ω1+ e−iθΩ2|, both oftlrandrlrcan reach the minimum value of 0.But when the photon incidents from the right of the waveguide, it can propagate freely.Thus, the frequency of the photon for realization of the perfect diode is shifted fromωbtoωTlr=0=ωb ±|Ω1+ e−iθΩ2|.One can use dressed state picture to understand this effect.When the transition between|b〉 and|c〉 is driven by the two fields, the statesplits into two states with frequencyωb+|Ω1+e−iθΩ2|andωb −|Ω1+ e−iθΩ2|, respectively.Thus, when the photon with frequencyωb+|Ω1+e−iθΩ2|orωb−|Ω1+e−iθΩ2|incidents from the left, it will be scatted into the free space.It is interesting to note that if the system is driven by a single coherent field,for the resonant photon withω=ωb,one needs to turn off the coherent field to realize the diode.But in this proposal, instead of turning off the two coherent fields, one can manipulate the phase differentθto the realize the diode effect for the resonant photon while the coherent fields keep on.
SinceωTlr=0depends strongly on the phase differenceθ,one can manipulate single photon asymmetric transmission by controllingθ.It is easy to obtain that when

the photon will be scatted into the free space.Here,we have supposed Ω1=Ω2=Ω0.Figure 2(a) showsTlr ≡|tlr|2as functions ofθandω.It exhibits that whenδ=ω −ωb=±2Ω0,θ=2nπ,Tlrreaches the minimum value of 0.nis an integer.The results are consistent with the theoretical analysis.Figure 2(b)is cut from Fig.2(a).It exhibits clearly that one can controlθto realizeTlr=0.It is also notable that whenθ=(2n+1)π,Tlrreaches the minimum value of 0 for the resonant photon even the two coherent fields keep on.This effect results from the destructive interference between the two driving fields.
3.2 Nonideal Case
Fig.3 (Color online)Phase difference controlled Tlr (a)and∆T (b).In the calculations,γb=0.75Gr,Gl=0.25Gr,Ω0=0.1Gr.
Now, we study the asymmetric transmission of single photon in the case ofGl≠ 0.We first discuss the case ofγc=0.One can find from Eqs.(5a), (5b) that ifGr=Gl+γb, andθsatisfies Eq.(7),tlrreaches the minimum value of 0.It means that the single photon can not transmit from the left to the right.However, if the photon incidents from the right, the transmission is not zero.Thus, one can realize the asymmetric transmission.Different from the case ofGl=0,Tlrcan not reach the maximum value of 1.To describe the degree of the asymmetric transmission, we introduce
whereTrl=|trl|2.If there is no asymmetric transmission effect,Tlr=Trl=0, thus ∆Treaches the minimum of 0.However, ifTlrorTrlis zero,|∆T|is equal to 1.The degree of the asymmetric transmission reaches the maximum value.It is easy to check that whenGr −Gl=±γband cosθ=[(ω −ωb)2−2Ω20]/(2Ω20), ∆Tcan reach∓1.So, one can control ∆Tby manipulatingθfor the fixedΩ0.Figures 3(a) and 3(b) respectively showTlrand ∆Tas functions ofθandδ.It exhibits clearly that for a givenδ,one can manipulateθto reach high value of ∆T.It also shows that whenδ=0, one can tuneθto be (2n+1)πto obtain ∆T=1.γcis often neglected in many reports.However, it can strongly affect the results ifγcis comparable withγb.Equation (5a) shows that if

are satisfied,tlr=0.Figures 4(a) and 4(b) showTlras functions ofθandδwithγc=0.1Grandγc=0.5Gr,respectively.It exhibits clearly that the maximum values ofTlrare different due to population leaking.Figures 4(c)and 4(d) exhibit ∆Tvarying withθandδfor the cases ofγc=0.1Grandγc=0.5Gr, respectively.It shows that the values ofθfor getting the maximum values of∆Tare quite different, which is consistent with previous analysis.Thus,γcmay play important roles in coherently controlling the single photon diode.

Fig.4 (Color online)Phase difference controlled single photon transmission when γc is not zero.(a)and(c)respectively exhibit Tlr and ∆T with γc=0.1Gr as functions of δ and θ.(b) and (d) respectively show Tlr and ∆T with γc=0.5Gr.In the calculations, Gl=0.25Gr, γb+γc+Gl=Gr, Ω0=0.1Gr.
4 Summary
In summary, we investigated coherent controlling single photon asymmetric transmission in the atom-waveguide system with chiral coupling.We deduced the conditions to reach the maximum value of ∆Tfor the cases with and without considering ofγc.The degree of asymmetric transmission ∆Tcan reach the ideal value of±1 by manipulating the phase difference between the two coherent fields even for the resonant single photon.The results may find applications in designing all-optical quantum devices at single-photon level.
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Numerical Study on the Whole Process of Fireball Evolution in Strong Explosion∗
- Neural-Network Quantum State of Transverse-Field Ising Model∗
- Magnetocaloric Effect in Anisotropic Mixed Spin–1 System:Pair Approximation Method
- Structure, Electronic, and Mechanical Properties of Three Fully Hydrogenation h-BN:Theoretical Investigations∗
- Similar Early Growth of Out-of-time-ordered Correlators in Quantum Chaotic and Integrable Ising Chains∗
- Fractional Angular Momentum of an Atom on a Noncommutative Plane∗
