200 km/h中速磁浮最小竖曲线半径取值研究

易思蓉 杨冬营 吴跃成

(1.西南交通大学， 成都 610000；2.四川省公路规划勘察设计研究院， 成都 610041)

磁浮轨道交通系统噪声低、转弯半径小，爬坡能力强，且最具速度拓展优势，契合轨道交通系统的技术发展需求，因此国内外就相关技术的研究一直在持续。与德国、日本的高速磁浮系统发展研究不同，国内学者重点研究和推广低速磁浮技术。已投入运营的磁浮线有长沙磁浮线、北京磁浮线和广东清远磁浮线。长沙磁浮线的最高运营速度为140 km/h，其它线路最高运营速度只有100 km/h。目前，对160～250 km/h中速磁浮系统的技术研究在稳步推进。王国静[1]等对中速磁浮列车的车体强度进行了验证；梁潇[2]等分析了低速磁浮改造升级为中速磁浮的关键技术；王家恒[3]等对中速磁浮车辆设备连接箱结构进行了有限元仿真分析；杨颖[4]等总结了中速磁浮列车的技术创新点，展望了中速磁浮的应用前景；侯圣杰[5]研究了高速磁浮灾害预警系统。在完成“十三五”国家重点研发计划课题“中速磁浮交通系统关键技术研究”中，中国中车集团有限公司已推出200 km/h级中速磁浮列车，但相应的线路技术标准未做系统性研究，本文分析相应系统的最小竖曲线半径取值。

磁浮列车牵引力极强，其最大坡度在70‰以上。但大坡道易产生较长的竖曲线，竖曲线半径取值成为影响纵断面线形设计灵活性的关键因素。轨道交通竖曲线半径取值的研究方法包括静力学计算和动力学仿真分析。易思蓉[6]根据上海磁浮示范线的实践经验从静力学角度提出了高速磁浮系统的线路技术条件，分析了竖曲线半径的控制性因素；赵树森[7]在构建车-线动力学模型的基础上，分析了竖曲线与平面圆曲线重叠、竖曲线与缓和曲线重叠设置时动力性能的变化；王代富[8]通过动力学仿真，总结得出高速铁路不同形式和不同半径的竖曲线对车-线系统响应的影响规律；葛岱[9]利用多体动力学仿真软件研究旧式低磁浮系统的竖曲线参数标准。本文参照中国中车集团有限公司新一代中速磁浮列车的技术参数，利用SIMPACK软件建立车-线动力学模型，依据列车运行的舒适性、安全性评价指标，仿真分析垂向加速度、悬浮间隙、垂向力和减载率的变化规律，兼顾静力学计算结果，确定与新型磁浮列车相适应的最小竖曲线半径取值。研究结论可为中速磁浮系统的实施提供参考依据。

1 中速磁浮车-线动力学模型

1.1 新型磁浮列车动力学特征

新一代磁浮系统的车辆和轨道梁模式类似于上海高速磁浮示范运营线车辆模式，与长沙中低速磁浮系统式的F轨不同，其走行部分由5个悬浮模块组成，车体的俯视图、纵向剖面图和横向剖面图，如图1、图2所示。基于图2所示的拓扑关系，可利用SIMPACK动力学仿真软件建立中速磁浮车-线动力学模型，具体包括悬浮架建模、控制系统建模和线路建模。

图1 车厢俯视图

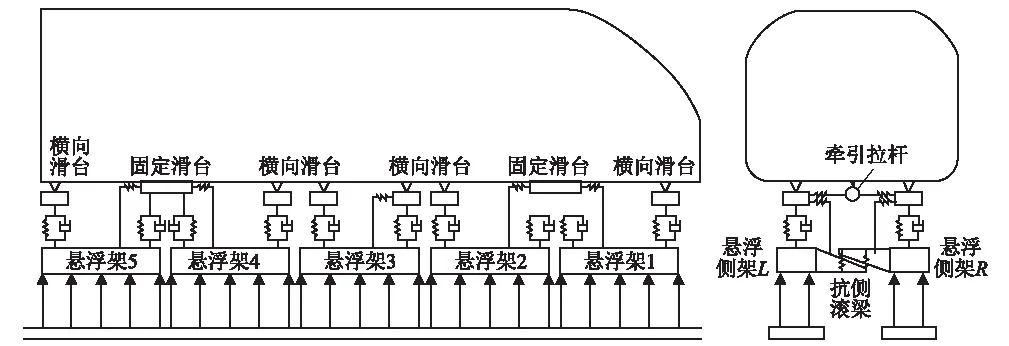
图2 车厢剖面及拓扑关系图

建模过程中，对车体、悬浮架和轨道结构，以及三者间的复杂作用关系进行了简化，包括[10]：(1)视各独立结构为刚体；(2)悬浮架相对车体中心对称布置；(3)忽略外部纵向力的影响。

1.2 悬浮架建模

悬浮架的主要部件装置包括托臂、纵梁、抗侧滚梁和牵引拉杆，如图3所示。2个托臂和1根纵梁组成1套悬浮侧架，2套悬浮侧架由中间的4根抗侧滚梁对接组成悬浮架的主体结构，抗侧滚梁负责调节悬浮架在轨道上的位置。悬浮架中间配有牵引拉杆，与牵引电机相连，构成悬浮架的动力源。悬浮架顶部为4组空气弹簧和滑台。空气弹簧是磁浮车辆的减振装置，使列车运行具有舒适性。滑台负责动态调整车体在弯道上的姿态，使列车运行具有平稳性。悬浮架各部件在SIMPACK中的参数如表1所示。

表1 悬浮架建模参数表

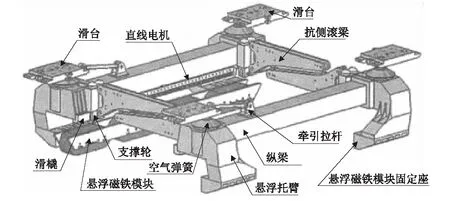
图3 悬浮架结构图

1.3 悬浮控制系统建模

位于悬浮架和轨道间的悬浮控制系统通过调节电磁吸引力来稳定车体的悬浮状态。悬浮架上的传感器实时获取悬浮间隙，悬浮控制系统利用电流调节装置将悬浮间隙控制在8 mm±2 mm范围。利用悬浮架与轨道间的垂向耦合力，可以建立式(1)所示的关联方程，并据此完成悬浮控制系统建模。

(1)

式中：F——电磁力(N)；

μ0—真空磁导率；

N—电磁铁线圈匝数；

A—有效磁极面积(mm2)；

i—电磁铁电流(A)；

δ—悬浮间隙(mm)。

1.4 线路建模

线路模型包括几何线形和轨道不平顺两个部分。SIMPACK的线路模块可定义仿真分析时的各类几何线形，轨道谱模块可定义轨道不平顺参数。本文采用的轨道谱公式为：

(2)

式中：Ω——空间波数(rad/m)；

n——频率特制参数(一般取1.5～4.5)；

P——表面粗糙性洗漱；

C——修正等比级数。

以单节车体下的5个悬浮架为1组，建立相应的车-线动力学模型，如图4所示[11]。

图4 单节车整体模型示意图

2 静力学分析

对于常规低速轨道交通系统，可依据舒适度指标所规定的垂向加速度最大允许值，采用传统静力学计算方式确定最小竖曲线半径值：

(3)

式中：V——设计速度(km/h)；

amax——垂向加速度最大允许值(m/s2)。

由于新一代中速磁浮模型与上海高速磁浮示范运营线系统模型基本相似，因此，本文借鉴高速磁浮垂向加速度允许值，即凹型竖曲线一般情况下取1.0 m/s2，困难情况下取1.2 m/s2；凸型竖曲线一般情况下取0.5 m/s2，困难情况下取0.6 m/s2[12]。参照上述指标和静力学计算公式可计算出中速磁浮最小竖曲线半径参考值，计算结果如表2所示。

表2 静力学要求的最小竖曲线半径表(m)

静力学分析方法将车体视为刚体，无法考虑列车与轨道梁间冲击振动对垂向加速度的影响。当列车运行速度较高时，应进行动力学仿真分析和验证。

3 动力学仿真分析

磁浮系统纵断面线形的动力学评价指标包括垂向加速度、悬浮间隙、垂向力和减载率。其中第一项为舒适性指标，后三项为安全性指标。动力学仿真分析能够模拟出4项指标随竖曲线半径变化的规律，得出更合理的最小竖曲线半径取值。

3.1 垂向加速度变化规律

竖曲线起点是纵断面线形的振动敏感点[13]。当磁浮列车高速进入竖曲线时，线形曲率的突变会引起悬浮间隙的改变，列车控制系统调整悬浮间隙时将引发悬浮架的振动，产生垂向加速度的最大值，然后逐步消减为与竖曲线半径和轨道不平顺相关的垂向加速度稳态值，如图5所示。

图5 垂向加速度最大值与稳态值图

利用车-线动力学模型，仿真分析磁浮列车在凹型竖曲线上，半径位于 3 000～8 000 m区间的垂向加速度变化，如图6所示。

图6 凹型竖曲线上垂向加速度变化曲线图

基于异速生长函数可拟合出垂向加速度最大值曲线公式为：

a=210.265×R-0.629

(4)

式中：R——设计速度(km/h)。

垂向加速度稳态值曲线公式为：

a=331.795×R-0.721

(5)

依据垂向加速度允许值，按照式(4)和式(5)可计算出凹型竖曲线最小曲线半径，计算结果如表3所示。

表3 凹型竖曲线最小曲线半径表(m)

将计算结果对比可知，满足舒适度要求的凹型竖曲线最小半径，一般情况下可取 5 000 m，困情况下可取 3 700 m。

利用车-线动力学模型，仿真分析磁浮列车在凸型竖曲线上，半径位于 3 500～26 000 m区间的垂向加速度变化，如图7所示。

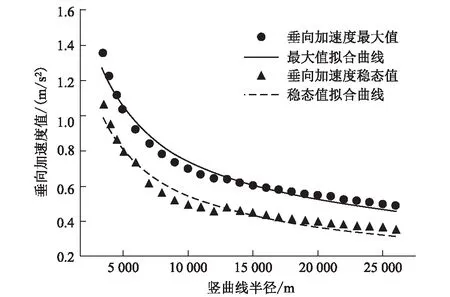
图7 凸型竖曲线上垂向加速度变化曲线图

基于异速生长函数可拟合出垂向加速度最大值曲线公式为：

a=80.963×R-0.510

(6)

垂向加速度稳态值曲线公式为：

a=101.901×R-0.569

(7)

依据垂向加速度允许值，按照式(6)和式(7)可计算出凹型竖曲线最小曲线半径，计算结果如表4所示。

表4 凸型竖曲线最小曲线半径表(m)

由计算结果可知，由垂向加速度最大值曲线确定的凸型竖曲线最小曲线半径，在一般地段已达到 20 000 m以上，困难地段也达到 15 000 m以上。如此大的竖曲线半径会对设计和施工造成不便：

(1)竖曲线长度过长，影响纵断面线形设计的灵活性，导致工程量的增加。

(2)轨道梁的曲率应与竖曲线一致，曲率过小的轨道梁难以进行施工控制。

(3)竖曲线起终点是空间线形的振动敏感点，轨道梁易产生沉降、偏移或变形，曲率过小则难以进行维修养护。

因此，在凸型竖曲线上，不建议采用垂向加速度最大值确定的最小曲线半径，而应采用垂向加速度稳态值确定的最小曲线半径。因此，满足舒适度要求的凹型竖曲线最小竖曲线半径，一般情况下可取 11 500 m，困情况下可取 8 400 m。

3.2 悬浮间隙变化规律

为保证垂向悬浮力不影响钢轨和车辆结构的稳定性与耐久性，磁浮列车运行时的悬浮间隙需控制在 8 mm±2 mm区间。利用车-线动力学模型，可仿真分析磁浮列车在半径为 1 500～10 000 m区间两种类型竖曲线上的悬浮间隙变化。动力学模型考虑了每个悬浮架下面的8个悬浮间隙控制器，按其中最大波动值进行统计，形成悬浮间隙变化如图8所示。

图8 悬浮间隙变化曲线图

由拟合曲线可知，在凹型竖曲线上，悬浮间隙大于8 mm，且随着竖曲线半径的减小而增大，此时磁浮列车处于“下沉”状态；在凸型竖曲线上，悬浮间隙小于8 mm，且随着半径的减小而减小，此时磁浮列车处于“过浮”状态。当竖曲线半径大于 2 500 m时，两种类型竖曲线上悬浮间隙均处于安全范围内。因此，竖曲线半径满足舒适度要求时，自然满足悬浮间隙安全值。

3.3 垂向力变化规律

单节车体下的5个悬浮架上共有40个控制器，每个控制器的最大电磁力为11 kN。由于相同竖曲线半径条件下，凹型竖曲线较凸型竖曲线具有更大的垂向力，因此只需分析凹型竖曲线上的垂向力变化规律。利用车-线动力学模型，仿真分析磁浮列车在凹型竖曲线上，半径位于 1 500～10 000 m区间的垂向力变化，如图9所示。

图9 凹型竖曲线上垂向力变化曲线图

由拟合曲线可知，当凹型竖曲线半径小于 5 000 m时，垂向力逐渐增大，当凹型竖曲线半径大于 3 000 m后，垂向力稳定在9.43 kN，小于控制器的最大电磁力值。因此，竖曲线半径满足舒适度要求时，自然满足垂向力安全值。

3.4 减载率变化规律

减载率是指磁浮列车运行时垂向力的减载量与静止状态垂向力的比值，且只在凸型竖曲线上存在。《机车车辆动力学性能评定及试验鉴定规范》要求减载率应小于0.8[14]。利用车-线动力学模型，仿真分析磁浮列车在凸型竖曲线上，半径位于 1 500～10 000 m区间的垂向力变化，如图10所示。

图10 凸型竖曲线上减载率变化曲线图

由拟合曲线可知，当凸型竖曲线半径大于 1 500 m时，即可小于规范要求的减载率最大值。因此，竖曲线半径满足舒适度要求时，自然满足减载率安全值。

综上所述，当竖曲线满足垂向加速度最大允许值所对应的最小竖半径时，悬浮间隙、垂向力、减载率3项指标可满足要求。

4 结论

本文参照中国中车集团有限公司最新研制的中速磁浮列车技术参数，建立相应的车-线动力学模型，在不同类型和半径取值的竖曲线上，仿真分析磁浮列车的垂向加速度、悬浮间隙、垂向力、减载率的变化规律，兼顾传统的静力学计算，依据相关规范要求确定最小竖曲线半径取值。

研究结果表明，对于中速磁浮系统，列车振动成为影响列车运行舒适度的重要因素，采用动力学模型计算得到的竖曲线半径较静力学计算大。当竖曲线半径值满足舒适性指标时，自然能够满足相关的安全性指标。为方便设计和施工，可将仿真分析结果向上取 1 000 m整倍数，即凹型竖曲线的最小半径一般情况下取 5 000 m，困难情况下取 4 000 m；凸型竖曲线的最小半径一般情况下取 12 000 m，困难情况下取 9 000 m。