面向大规模机器类通信的无速率编码调制技术

王莹莹， 孙 蓉， 程建华， 苏 丽， 夏晓靖

（1.哈尔滨工程大学智能科学与工程学院，哈尔滨 150001；2.上海机电工程研究所，上海 201109）

0 引 言

5G时代的发展，远程医疗、无人化工厂对于5G技术提出了新的要求。大宽带、大规模机器通信以及超高可靠低时延通信将为未来5G应用提供更多的机会与平台。超高可靠低时延通信（Ultra-Reliable Low Latency Communication，URLLC）对通信提出新要求，对关键基础设备和计算机之间的往返延迟小于1 ms，使其能够在极端的可靠性标准下运行。要在高信噪比的条件下实现高可靠的传输，不仅需要使用短码长的信道编码包传输数据，而且为了降低编码增益的损失，需要采取一种能够进行强纠错的信道编码技术。例如，文献［1］中使用低密度奇偶校验码（Low Density Parity-Check，LDPC）的编码与自适应调制和编码相结合，能够快速在物理层配置中实现数据的传输，但是由于不可预测的信道变化条件，会使无线网络信号时延大大增加。文献［2］中针对低时延、强抗干扰、高速传输等数据链系统应用场景的需求，提出基于LDPC的信道编码方案，并详细介绍了数据链系统中信道编码技术应用的现状以及LDPC码理论，研究了信道编码系统传输模型和最小和译码算法及其改进算法。文献［3］中针对未来6G对更高的频谱与功率效率，以及更高的可靠性与更低时延的技术指标需求，研究了基于LDPC码的混合多层编码（MLC）和比特交织编码调制（BICM）方案，与传统的BICM方案相比，所提方案能达到更好的误块率性能与更低的复杂度。在此基础上，面向未来6G移动通信中的高频段、高速移动场景，对新型波形技术——正交时频空（OTFS）调制技术的基本原理与性能进行了讨论和分析。

本文采用幅度相移键控（Amplitude Phase Shift Keying，APSK）调制方法，利用最小欧氏距离与系统误快率之间的关系，提出了一种高可靠、低时延的编码调制方案，并通过禁忌搜索算法对该编码调制方案进行了优化。

1 系统模型

系统模型如下：信息首先通过模拟喷泉码（Analog Fountain Codes，AFC）进行编码，生成编码符号，然后通过APSK调制发送到高斯信道中，终端使用联合映射算法进行译码，再将得到的信号以反馈的方式输出到发送端，若发送端接收到信号，则认为接受译码成功［4］。

假设长度为k的｛0，1｝信息序列b，经过权重集w，w中有D个不同的权重，码字的度为L的固定度分布，使用渐近边生长算法（Progressive Edge-Growth，PEG）编码方式得到模拟喷泉码［5］，码字为

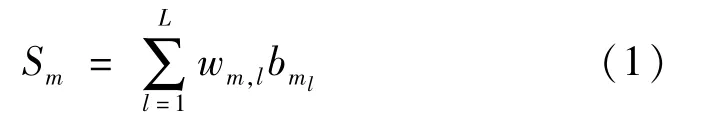
编码后的集合中码字的种类有2D，码字X通过调制后［6］，表达式如下：

式中：λ是APSK总环数；θi是第i个环的相位旋转的度数；ni是第i个环上的点的个数；Ri是第i个环的半径。

当码字X通过分析信道加性噪声的理想模型后，接收端接收到信号可表示为

式中，N～N（0，σ2）服从均值为0，方差为σ2的高斯分布［7］。

接收端使用联合解映射的算法进行调制和编码，得到接收端信号的估计值b′。估计值则通过反馈的通道将信号传送到发送端。若发送端接收到反馈的信号，则认为系统信息传输成功，结束当前码字的生成与传输。信道状态的好坏将决定着AFC码率的高低。因此要降低反馈传输时延，需要通过有限反馈，改变发送端的码率［7］。

2.1 APSK星座上符号的放置

APSK星座图上每环上的星座点计算公式为

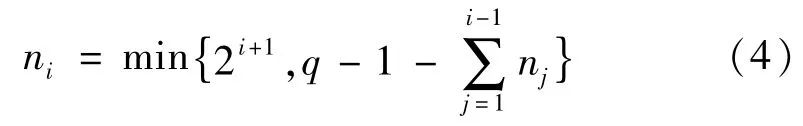
式中：i∈｛1，2，…，λ｝；q为总星座点数，为已知量；nj表示第j个环上的点数。

APSK的环半径公式为

式中，D为编码的长度。

星座图上符号的放置过程如下：

AFC接收端接收的信号Y可以由符号X以及分析信道加性噪声的理想模型表示：

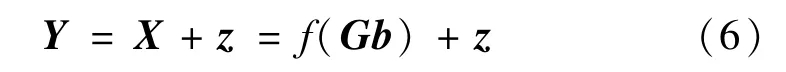
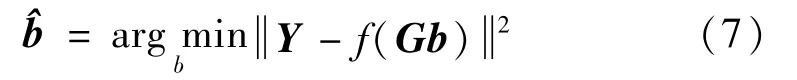
设b′与b相比至少有1 bit不相同，则其出现成对错误的概率为

式中：

帧错误概率PF是系统平均吞吐量的主要特征，其计算公式为

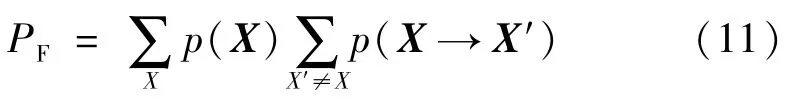
式中，p（X）＝1／2k。PF的下限可表示为

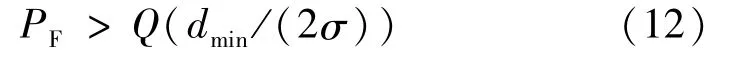
dmin为最小码字距离，其最佳平方码字距离的表达式为

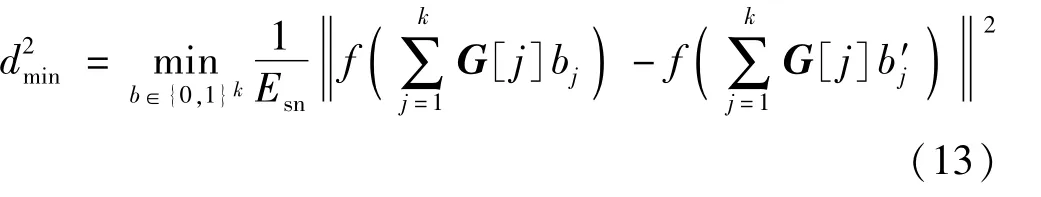
因为设b′与b相比至少有1 bit不相同，那么其余比特相同，展开公式为

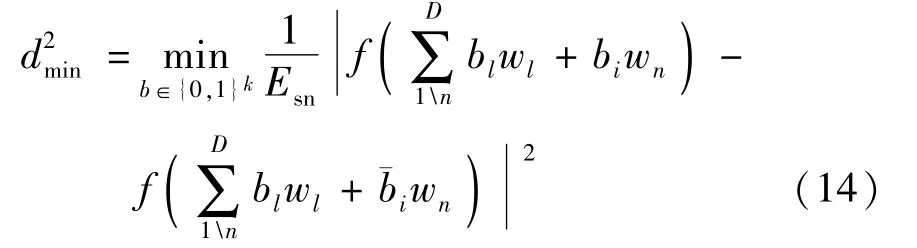
进而可以得到：

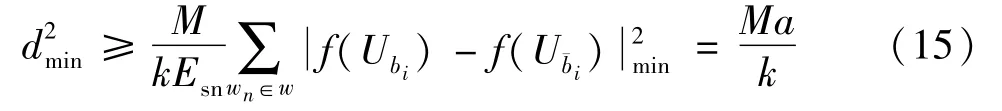
式中：

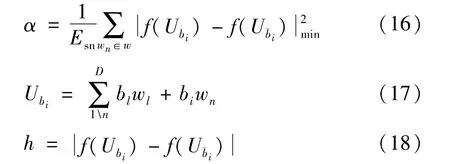
M为AFC编码后的码字长度；k为输入信息长度。将只有一位的比特错误的平均欧式距离定义为同理，可以推广到只有p位比特具有错误的最小欧式距离：

早期的唐草风格基本指的就是亚利桑那和加州风格。其特点是纹样的边线处理不规则，并且随型的比较多。之所以叫亚利桑那风格,是因为图案中出现的花卉纹样是采用亚利桑那特有花卉图案。花托部分的装饰线条是Y形纹排列，中间用刀线从上往下隔开。装饰性的茎干数量小，弧度小，卷草粗大，头部收缩卷曲，用圆点图案在中心收节。枝叶部分是采用欧式的茛苕叶。刀线走得窄而深。

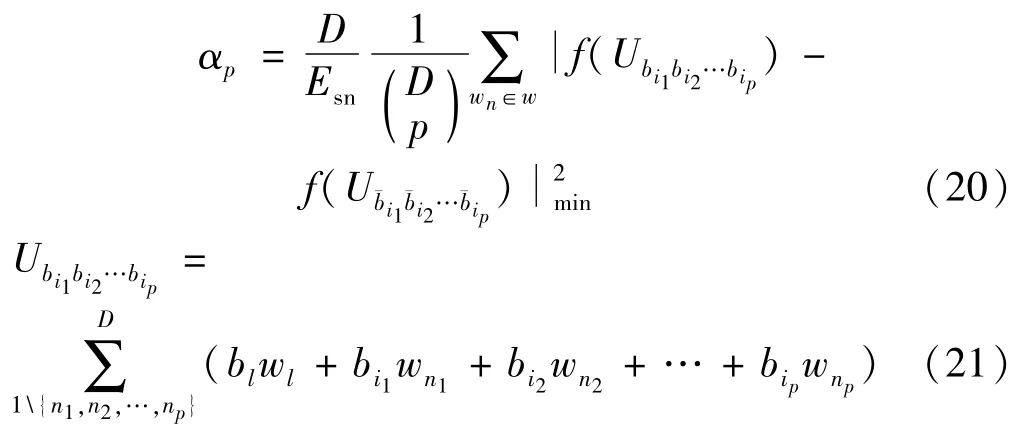
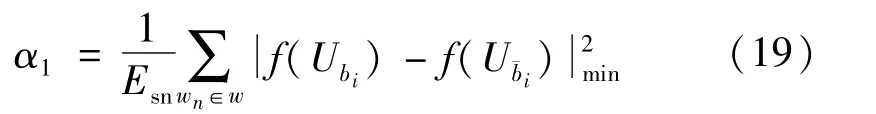
2.2 P-ASPK优化放置原理［8］

由上述推导ASPK放置原理的过程可以得到，如果保证α2＞α1，就可以得到两位比特发生错误的欧式距离将会小于一位比特发生错误的欧式距离。则就会得到两位比特发生错误的概率小于一位比特发生错误的概率，从而能够达到优化的目的。同理，如果保证αD最大时，同时要保证αD－1最大可能的大，同理，也要保证αD－2尽可能的大，这样就可以实现星座的最优放置［10］。其算法如下：

输入 AFC的权重集w，度D

输出 最佳的星座映射矩阵X

1.令α1best＝0，α2best＝0，…，αDbest＝0。

2.开始第1次寻优计算k＝1。

3.计算当前映射矩阵Xmay的α1，α2，…，αD。如果αD＜αDbest，继续第4步；如果αD＞αDbest，则α1best＝α1，α2best＝α2，…，αDbest＝αD。D＝D－1，重复步骤3。

4.k＝k＋1。

5.重复步骤3、4，直到k＝2D。

2.3 基于禁忌搜索算法的APSK优化算法

禁忌搜索（Tabu Search或Taboo Search，TS）算法其主要的思想是模拟人类的记忆，将刚刚搜索的状态放在禁忌表中，防止禁止算法再次搜索这种状态，从而能够提高解的质量［11］。

定义一个组合优化问题是对离散事件进行编排等，是对数学模型得到优解［12］。可用3参数（Q，F，f）表示，其中Q表示决策变量的定义域；F表示可行解区域，F中的任何一个元素称为该问题的可行解；f表示目标函数，Q上的一个映射：

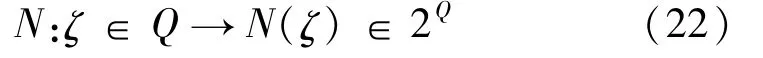
称为一个邻域映射，其中N（ζ）称为H＝Ø的邻域，2Q表示Q的所有子集的集合的数目［13］（见图1）。

图1 禁忌搜索算法流程图

由P-ASPK优化放置原理可知，优化后的星座需要保证αD最大时，αD－1尽可能地大，同时αD－2也尽可能地大，以此类推。所以在对两种不同优化放置方案进行比较时，首先比两星座的αD，选择较大的星座。如果αD相同，那么需要比较αD－1，以此类推，为了阐述简单，假设αD，αD－1，αD－1…α2都相同，对α1进行比较［14］：

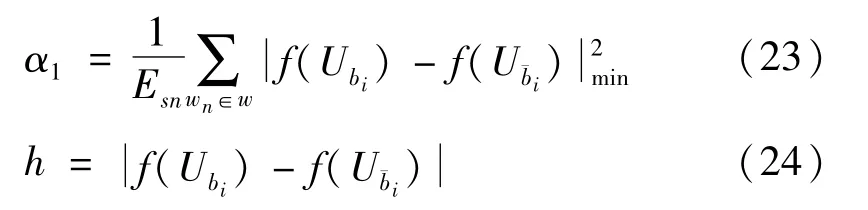
可以看出，基于APSK的优化原理可知，1／Esn是一个常值，不同的方案仅受h2min的影响，其中h2min表示星座之间的距离。2Rλ表示最长欧式距离［15］，则：

式中，Rλ满足：

λ为最大环数。由每环上的星座点的放置公式可得，星座的总点数范围为［2λ＋1－3，2λ＋2－4］，其具体的不同环数对应的点数范围不同。

基于禁忌搜索算法的APSK优化算法，主要包括两个过程，首先，确定Gray-APSK的星座参数，具体流程图如图2所示。其次，利用禁忌搜索算法在所有的可能的星座方案中寻找最优的星座方案。算法流程如下：

图2 确定Gray-APSK的星座参数流程图

输入初始星座放置p，目标函数f，可行解区域F，最大的迭代次数NG。

输出最佳的星座放置pmax。

1.初始星座放置p，禁忌表H＝Ø，禁忌长度T，最大的迭代次数NG，pmax＝p，j＝1。

2.在pmax的邻域内计算目标函数，找到目标函数最大的解设置为pmax，并存放至禁忌搜索表中。

3.j＝j＋1。

4.重复步骤2、3，直到j＝NG。

3 仿真验证

3.1 星座仿真优化结果

为验证本文所提出的优化算法的有效性，本文分别选择8APSK、16APSK和32APSK的星座图进行优化。优化后的星座图为8P-APSK、16P-APSK和32PAPSK。优化前、后的星座图如图3所示。

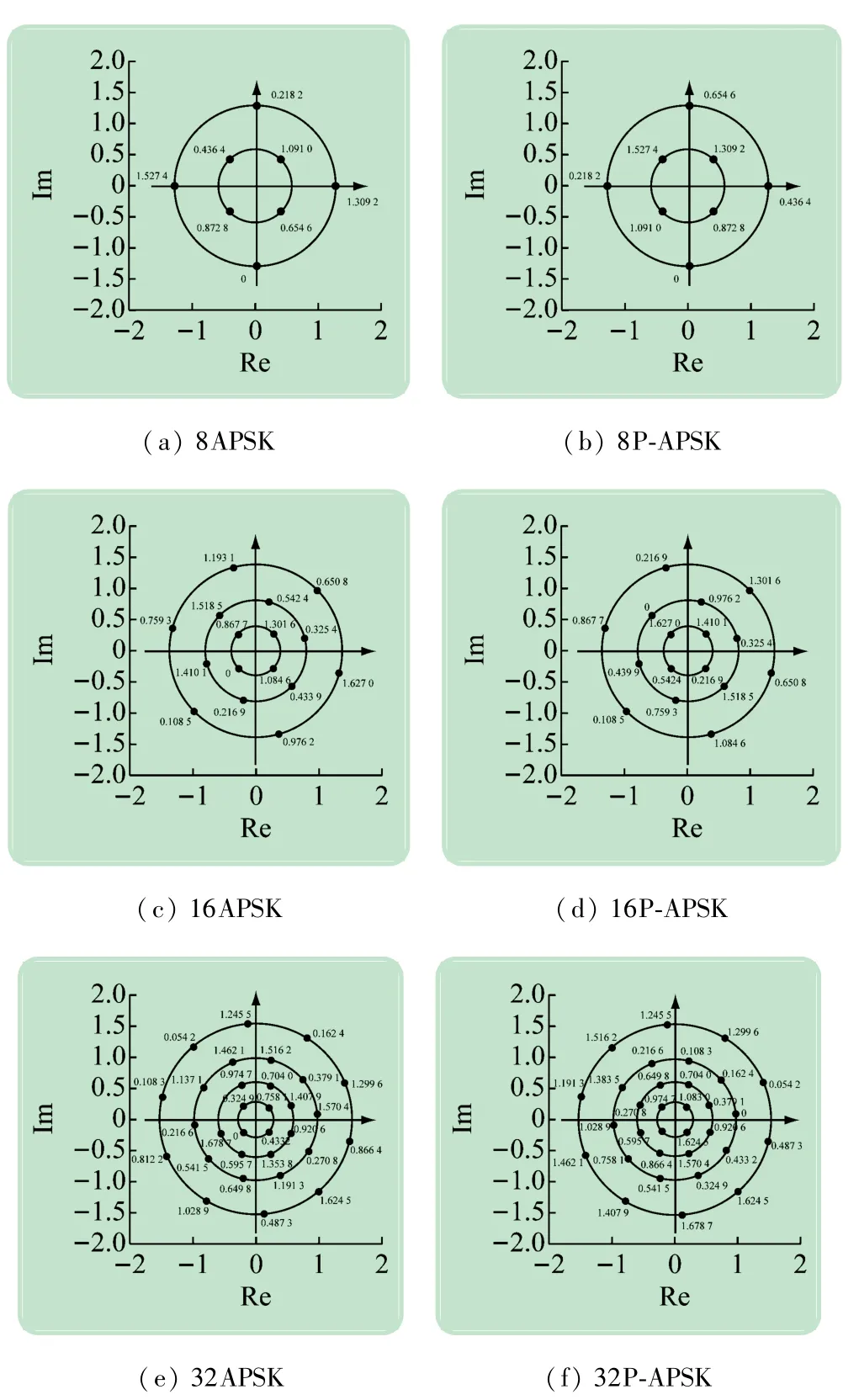
图3 优化前、后的星座图

经过计算，可得6个星座图的平均欧式距离α的值，如表1所示。由表1可知，优化前的APSK星座图的α1要比优化后的P-APSK的星图α1大，这说明优化前的星图发生一位比特错误的概率较小，但是通过比较α2，会发现优化前的星图要比优化后的星图发生两位比特错误的概率大。优化后的星图是在最大化α2的前提下，最大化α1，同理，对于D位比特来说，PAPSP需要在αD足够大的条件下，使αD－1，αD－2…α1也足够大，通过比较优化前后的α值大小，可以看到该优化方法能够实现预定的目标。

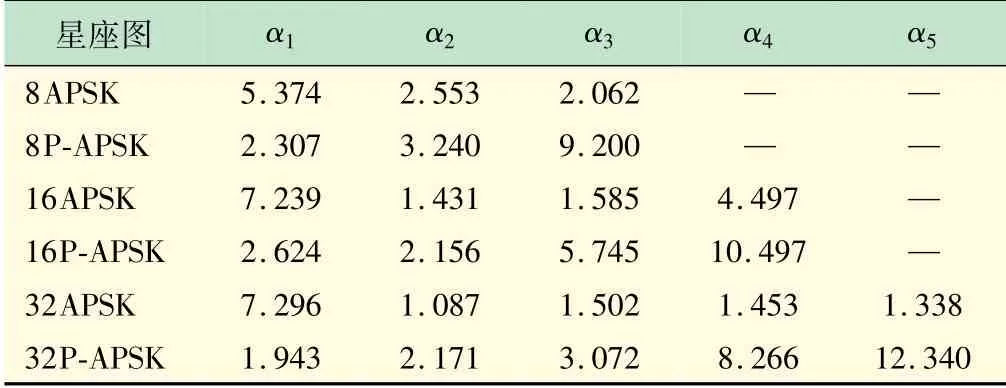
表1 不同星座图的α值

3.2 误块率分析

误快率是衡量星座性能的重要指标，本文分别在不同的权重集w和不同码字度D情况下分析3种不同的APSK（标准APSK、P-APSK、DVB-S2标准中的APSK）的误块率。其中码字度与权重集的取值见表2。

表2 权重集与码字度取值

上述编码通过3种不同的码率（R＝0.5，R＝1和R＝2）处理后，经过均值为0，方差为σ2的分析信道加性噪声的理想模型，后经过解映射算法进行联合编码调制译码，在不同的信噪比下得到不同星座的误块率如图4所示。

由图4可知，误块率随着码率的增加而增加，在保持码率不变的情况下，P-APSK的误块率性能比DVB标准中的误块率性能提升1 dB，这说明P-APSK优化方法在降低星座方案的误块率方面具有一定的优势。

图4 不同D星座图的误块率曲线图

3.3 复杂度分析

算法的时间复杂度是关于输入规模η的函数，该指标能够直观地反映算法的性能与收敛速度。禁忌搜索算法主要操作包括计算初始解，产生邻域以及更新邻域表等操作，其每步的操作复杂度见表3。其中：Ω为候选集的个数；ϑ为优化后候选集的个数。

表3 禁忌搜索算法操作复杂度

F为目标函数的复杂度，这里的目标函数为

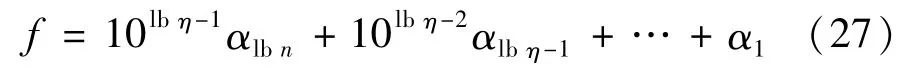
目标函数时间复杂度为

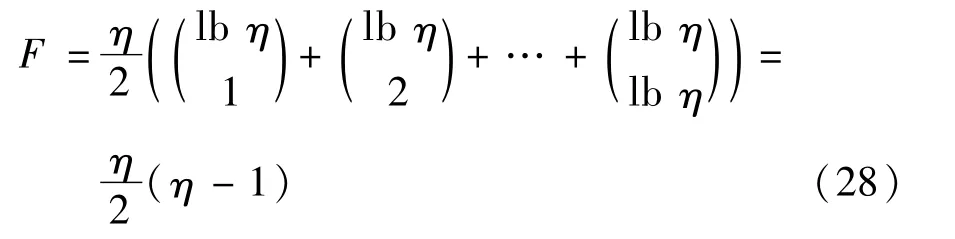
因此，总的时间复杂度为

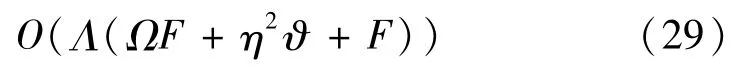
原始算法的复杂度为O（η！F），故两种算法的时间复杂度的比较见图5。由图5可知，随着输入规模的增加，两种算法的时间复杂度差距越大，在16APSK

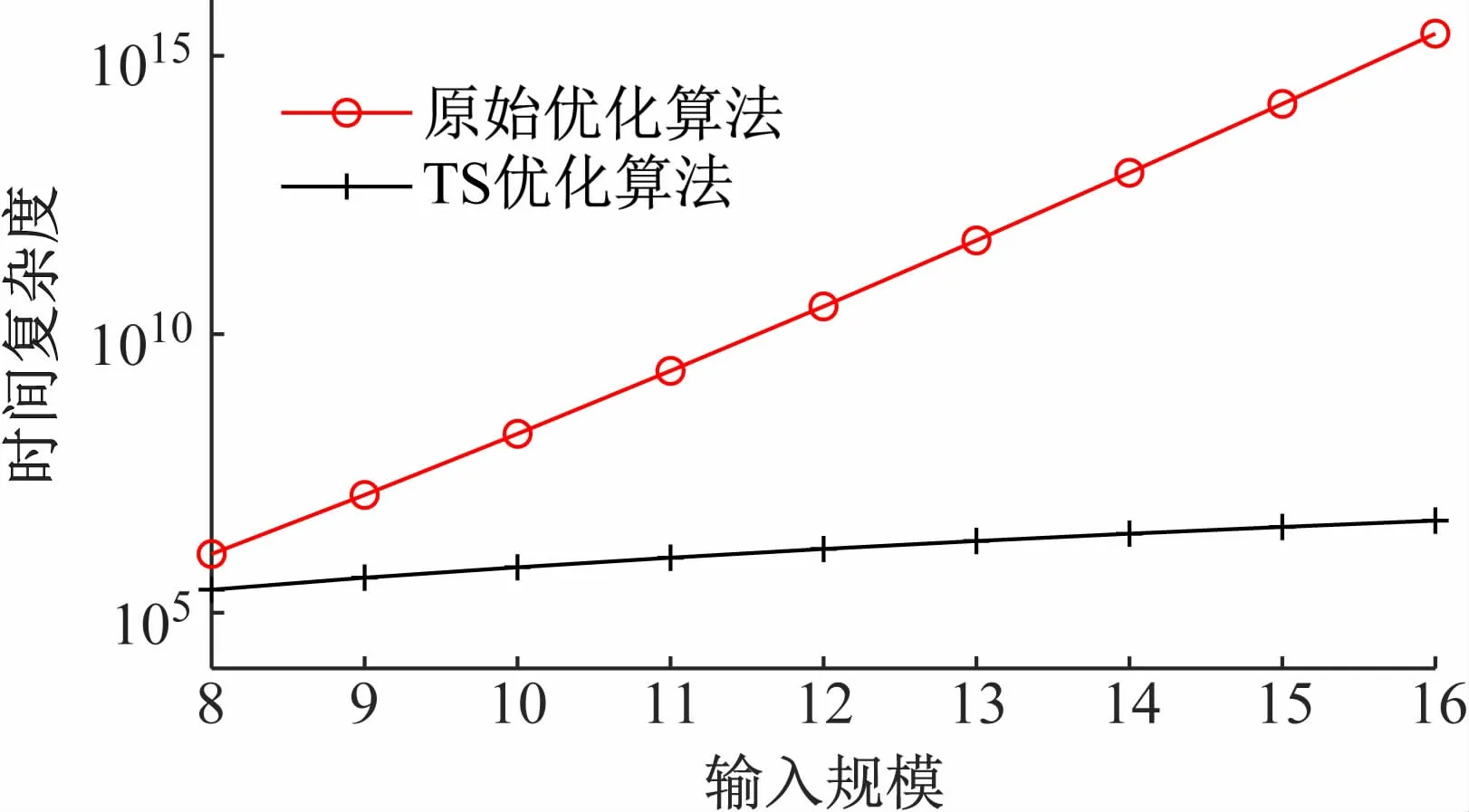
图5 两种不同优化算法的时间复杂度对比

的优化方案中，TS优化算法能够将原始的优化算法的复杂度从1015降低到107，优化效果明显。

4 结 语

本文为提高编码调制的可靠性与灵活性，提出了APSK调制方式，并且根据AFC的特点对APSK进行了优化，提出了P-APSK的优化方法。通过仿真实验验证，该方法的误块率比普通的APSK方案性能高1 dB。同时为减小P-APSK的计算量，采用了禁忌搜索算法。仿真结果表明，随着输入规模的增加，其时间复杂度降低的效果越明显。