顶板-纵肋焊接残余应力松弛效应研究

刘 昊, 王巍然

(1. 西南交通大学，四川成都 610031; 2. 兰州大学，甘肃兰州730000)

正交异性桥面板由于其轻质高强的力学性能，在大跨度桥梁中得到了广泛的应用。

然而，由结构构造和受力特性所决定，正交异性钢桥面板的疲劳问题突出。其中，纵肋与顶板连接焊缝(RD)和纵肋与横隔板焊缝(RDF)处疲劳开裂发生比例分别为30.2%和61.0%，比重最大[1]，疲劳问题严峻。而存在焊缝，就存在焊接残余应力。

近年来，针对焊接残余应力对钢桥疲劳性能的影响，学者们做了大量的试验研究。针对RDF细节，周绪红等[2]对正交异性钢桥面板节段模型单面焊RDF细节进行了单双轮加载并得到了该位置应力影响面，结果表明单面焊RDF细节横向应力以受压为主且焊根处应力幅显著高于RD细节。王春生等[3]通过足尺疲劳试验研究表明纵肋与横隔板交叉细节在压-压疲劳应力循环作用下发生开裂，究其原因是该位置存在较大的焊接残余应力。郭亚文[4]结合钢桥面板单面焊和双面焊RDF细节2类常见形式，针对该细节疲劳性能进行了较为深入的研究，研究表明2类细节裂纹萌生点位置应力特征均为压-压应力循环，该处发生疲劳开裂的必要条件为其位置存在焊接残余拉应力。

然而，RD细节在跨中加载时，内侧焊根同样受到压-压应力循环，同样存在焊接残余应力，但在实验中其疲劳开裂位置往往不是加载位置正下方，而是加载位置两侧拉-拉应力循环区。本文通过建立焊接残余应力与跨中荷载耦合模型模拟实际实验条件，以深中通道跨海大桥钢桥面板结构疲劳试验研究为例，深入研究焊接残余应力及其松弛效应对疲劳开裂位置的影响，解释RD与RDF细节开裂位置迁移的原因。

1 循环塑性本构模型

当构件承受的外荷载与残余应力叠加以后大于材料的屈服强度时，材料会由于塑性变形而导致残余应力发生松弛。本文采用Chaboche混合硬化模型，该模型包括运动硬化模型和基于Von Mises流动规律的非线性各向同性硬化模型，考虑了循环强化对棘轮效应和应力松弛效应的影响。

模型采用Q345钢，具有运动学和各向同性硬化变量的Von Mises屈服准则表示为：

式中:f是Von Mises屈服函数；s和a分别是二阶偏应力和应力张量；σ0是各向同性变形抗力，张力运算符“：”表示二阶张量的内积。

假设材料微变形，总应变由弹性应变和塑性应变组成：

ε=εε+εp

式中:ε、εε和εp分别为总应变、弹性应变和塑性应变。

因此，总应变增量可以写成：

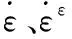
用材料耗散势积分柯西应力张量来确定弹性应变的变化速率，而且塑性应变增量张量与塑性流动沿垂直于屈服面的方向发展的屈服函数相关。因此，塑性流动规律可以写成：

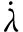
当与焊接残余应力结合的应力状态超过循环载荷下的弹性极限时，材料发生硬化。采用与各向同性硬化相关的运动硬化规则：

式中:m为背应力的数量；γk和Ck分别是各向同性硬化变量和运动硬化变量。各向同性硬化变量和运动硬化变量描述了塑性变形不同阶段的非线性变形。在本研究中，考虑了3种背应力运动硬化(m=3)。累计塑性应变率可由式(1)获得：

(1)

Chaboche采用了运动硬化准则和非线性各向同性硬化，考虑循环硬化及其对材料循环应力-应变响应的影响，如棘轮效应、应力松弛等。各向同性硬化规则表示为：

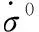
循环塑性本构模型包括一些因素，即C1、C2、C3、γ1、γ2、γ3、Q和b。各向同性和运动硬化变量(C1、C2、C3、γ1、γ2和γ3)见表1。材料常数(Q和b)通过与循环峰值应力相关的应变硬化曲线和全循环加载试验的累积塑性应变确定；对于Q345qD钢，Q=28，b=6.8。钢板和焊接材料采用相同的循环塑性本构模型。

表1 Q345钢的材料参数

2 焊接残余应力松弛效应分析

2.1 模拟过程

以深中通道跨海大桥钢桥面板结构疲劳试验研究为例，建立足尺单面焊模型，其中包括2个步骤：①采用热-力顺序耦合方法模拟焊接全过程;②采用实验加载方式，模拟在不同循环次数后残余应力松弛情况(图1)。

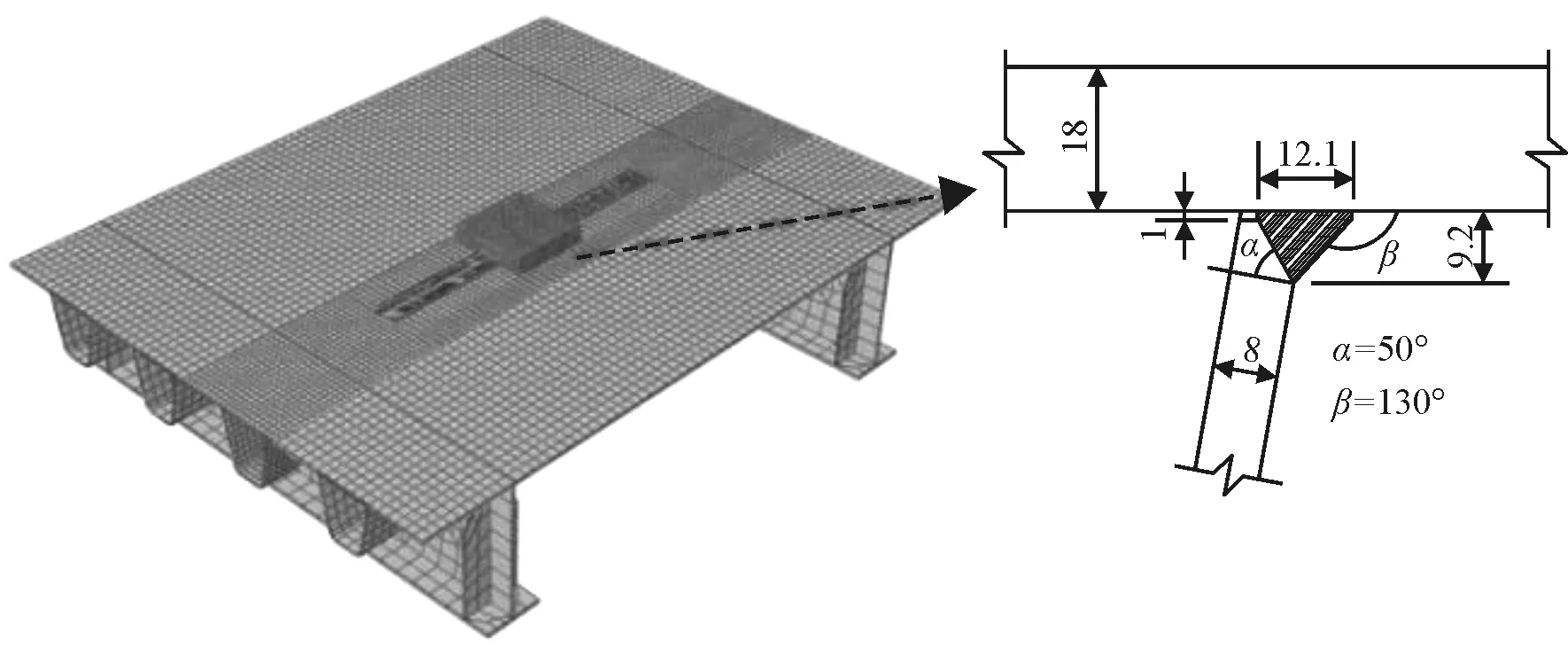
图1 有限元建模

步骤①具体细节:采用建立三横隔板两跨的足尺试验模型，优化网格后整体单元数量为，整体节点数为，焊接部分网格尺寸最小为1 mm，如图2所示。材料参数为Q345钢的热力学参数及循环本构参数。焊接时，电弧电压和电流分别设置为(30±2) V和(300±20) A。假定气体保护金属极电弧焊的电弧效率为80%，焊接速度为380 mm/min。采用生死单元法及双椭球热源函数模拟实际焊接全过程。

步骤②具体细节:实验中采用了逐级加载的模式，荷载从240 kN增加到了480 kN，本模型中直接采用360 kN面荷载探究焊接残余应力松弛规律。

2.2 模拟结果

对结果进行整理，对比2种工况下焊缝受力特性：①不考虑残余应力松弛；②考虑焊接残余应力松弛情况。由于不同荷载循环次数下残余应力会不断松弛，但松弛大部发生在循环刚开始，故采用10次循环后的应力场作为松弛后残余应力场进行对比。且最大应力一般发生在焊根位置，因此使用焊根处横向应力来研究循环荷载下的残余应力松弛。图2显示了焊根处横向应力、纵向应力及Von mises应力松弛前后对比。

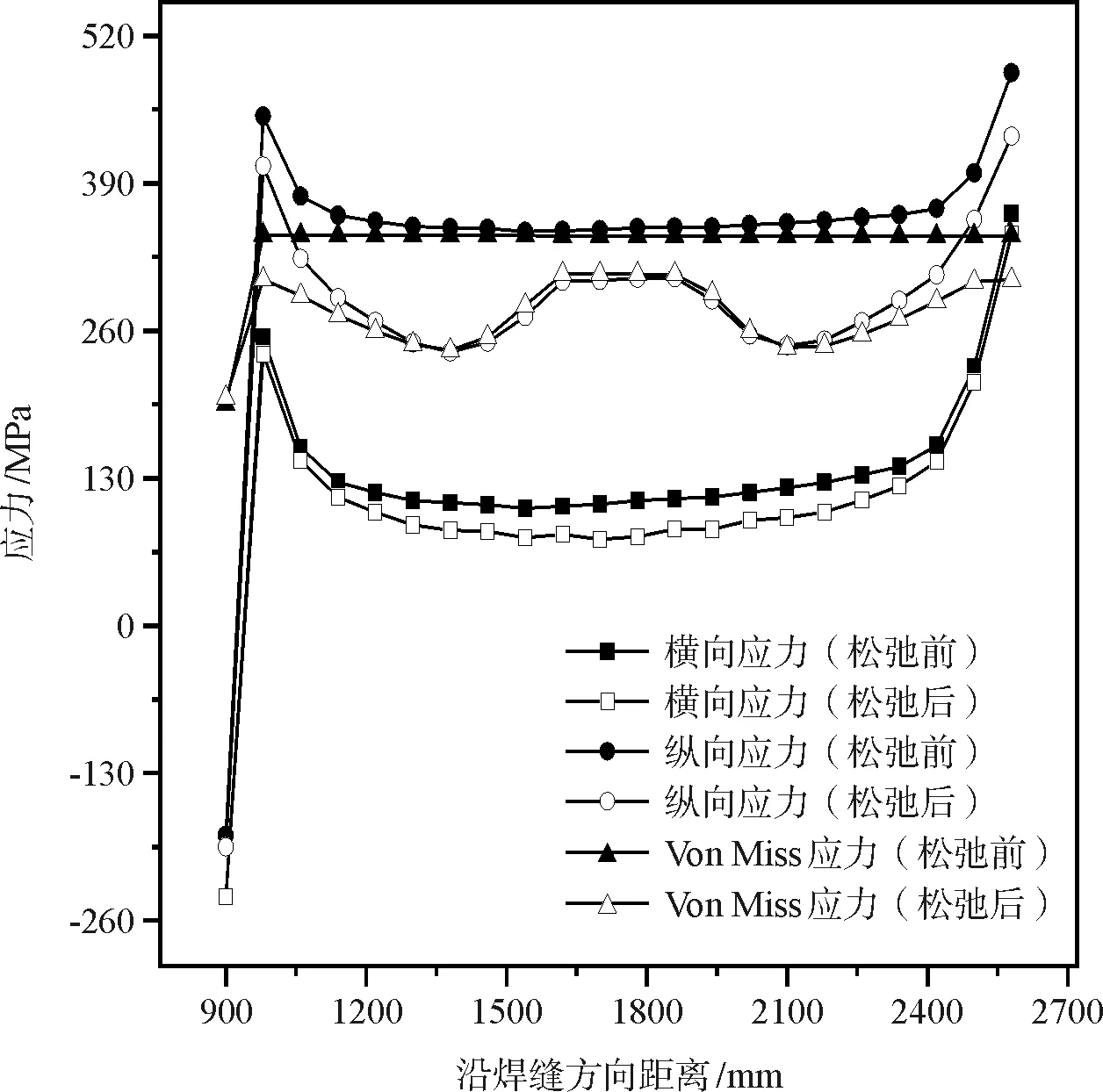
图2 横向应力沿焊缝方向分布规律

由图2可以看出，松弛前后，横向应力最大应力松弛幅度为32.816 MP，松弛比率为29.7%；纵向应力最大应力松弛幅度为109.31 MP，最大松弛比率为30.7%，Von mises应力最大应力松弛幅度为101.86 MP，最大松弛比率为29.6%。

横向应力与疲劳裂纹萌生和扩展直接相关，对于荷载正下方焊根疲劳细节，其横向应力由110.69 MPa下降到了71.87 MPa，在实验荷载下其横向应力循环特征在考虑残余应力松弛后由拉-拉循环变为拉-压循环。疲劳荷载幅值由95.11 MPa降低到71.87 MPa。

3 结论

在实验压-压外荷载循环下，荷载正下方焊根处疲劳细节存在较明显应力松弛现象，该处疲劳细节在松弛前后应力循环特征由拉-拉循环变为拉-压循环，疲劳荷载幅值变小，从而引起疲劳开裂位置迁移到了加载位置两侧拉-拉应力循环区，模拟结果符合实验现象。