基于异方差高斯过程回归的大坝变形预测模型

2022-09-23罗亦泳吴大卫张立亭刘宏宏

东华理工大学学报(自然科学版) 2022年1期

罗亦泳，吴大卫，张立亭，黄城，刘宏宏

(1. 东华理工大学测绘工程学院，江西南昌 330013；2. 南昌市新建区土地管理勘察测量队，江西南昌 330100)

目前，我国水库大坝面临大坝数量多、气候变化、建设条件复杂等多重因素带来的风险(中华人民共和国水利部，2018)。大坝在运营过程中受到水位、温度等多种复杂因素影响，大坝的安全将受到巨大的威胁。大坝变形监测技术是保障大坝安全运行的重要技术手段，通过建立大坝变形预测模型可及时掌握大坝变形发展趋势，为大坝安全预报预警提供可靠的理论依据(顾冲时等，2016)。因此，大坝变形预测模型研究是大坝安全监测的核心内容之一，对大坝变形灾害防治具有重要的意义。

近年来，大坝变形预测模型的研究成果较为丰富，主要包括确定性模型、统计预测模型及机器学习算法等(吴中如，2003；Mata et al.,2013；Liang et al.，2018；汪宏宇等，2021)。大坝变形是一个多因素影响的非线性系统，无法精确地掌握变形过程及机理。因此，确定性预测模型非线性映射能力不足，预测结果的精度有待于提高。大坝统计预测模型主要包括统计回归模型、时序分析模型(潘国荣,2005)、模糊数学模型和灰色系统模型(靖洪文等，2012)等，这类方法是一种经验模型，存在过度依靠数学处理、随机性大和预报时间短等缺点。随着机器学习方法的快速发展，机器学习算法在变形预测领域得到较好的应用。智能算法、人工神经网络模型被应用于大坝变形，该方法预测精度得到较大提高(陈俊风等，2020；王新洲等，2005；胡纪元等，2014；徐锋等，2012)。但神经网络模型存在局部最优、收敛慢、结构设计难，并且当样本较少时，预测精度不理想。针对神经网络模型的经验风险最小原则的缺点，提出基于支持向量机的大坝变形预测方法(王新洲等，2008；董明等，2017；宋志宇等，2007；张豪等，2011；罗亦泳等，2010；朱军桃等，2019)，但支持向量机存在核函数参数和损失函数难以确定等问题。基于极限学习机(ELM)构建了变形预测模型，预测结果的精度得到一定的提高(王晓玲等，2020)。但由于 ELM 对噪声敏感，且特征映射存在随机性，因此降低了算法的鲁棒性和泛化能力。当前研究成果表明，机器学习算法能较好地表达变形影响因素与变形量之间的复杂关系，是变形预测研究的发展趋势。当前研究主要集中在提高变形预测方法精度方面，而对预测结果的可靠性分析研究较少。用于变形的机器学习算法通常包含多个需要用户确定的参数，参数取值是否合理严重影响预测精度及可靠性。因此，需要构建一种参数自适应及结果可靠性高的大坝变形预测模型。

标准高斯过程回归(GP)是近年来一种基于贝叶斯网络的新型学习算法，对处理高维、小样本数据及非线性问题具有很好的适应性和泛化能力，并且参数自适应，可以输出预测变量的方差与期望，可分析结果的可靠性(苏国韶等，2008；Rasmussen et al.,2006; Gibbs,1997;Kocian et al.,2008)。因此，GP受到广泛关注而成为机器学习的研究热点，并已被应用于变形预测(罗亦泳,2016)。但标准的GP假定噪声为高斯分布，且整个数据集中噪声方差为常值。在实际的变形监测过程中，监测环境在不断地变化。因此，假设噪声方差为常数不符合实际，影响预测结果及可靠性。针对标准GP算法的上述缺点，GP的改进算法——异方差高斯过程回归算法(HGP)被构建(Kersting et al.,2007)。HGP算法将观测数据中的噪声方差作为变量，并利用高斯过程进行对其建模，基于变分推理进行解算。由于HGP算法充分考虑了数据中的噪声变化特征，其改进方法更加符合实际工程环境，可以有效提高算法实际应用效果(Rogers et al.,2020;Wang et al.,2019;Rodrigues et al.,2018; Lzaro-Gredilla et al.,2013)。鉴于HGP算法在处理复杂系统建模上的优势，笔者针对当前大坝变形预测模型存在的问题，提出一种基于异方差高斯过程的大坝变形预测模型，以提高变形预测结果的精度及可靠性，并与多种变形预测方法进行对比，验证新方法的有效性。

1 异方差高斯过程回归算法

标准的高斯过程学习算法将测量噪声的方差作为常数，但变形监测过程往往受到多种随机性因素干扰。因此，将噪声的方差看成常数进行建模和解算会影响算法的预测精度。对此，异方差高斯过程被提出应用于复杂系统的建模。相比标准高斯过程学习算法，该方法取得更好的预测结果。HGP是标准高斯过程算法的拓展，将建模过程分成两部分(Wang et al.,2019;史宇伟等，2014；Lzaro-Gredilla et al.,2011;严宏等，2018)。首先运用标准高斯过程对无噪声输出进行建模，然后对噪声再运用高斯过程进行建模，该方法能体现出变形监测量的随机性及波动性。

HGP算法将变形量分为两部分：

y=s+r

(1)

式中，y为变形监测值，s为时间t对应的理想标准值，r为对应的偏差项。

p(s,s*)～N(0,KN+1)

(2)

式中，KN+1为此多元高斯分布的协方差矩阵，具有如下的形式：

(3)

式中，k**=k(t*,t*),k*=[k(t1,t*)k(t2,t*)…k(tN,t*)]T,KN如式(4)所示。k(ti,tj)为核函数，通常采用squared exponential核函数(史宇伟等，2014)。

(4)

因此，可以利用标准高斯过程的结果计算测试集中时间t*对应的标准值s*的后验分布，计算公式如下：

(5)

(6)

(7)

利用高斯过程原理分别对标准值和偏差项建模后，需要对模型进行解算，求解超参数，最终得到预测变量的验后分布(期望和方差)。根据标准高斯过程的推导结论，可以计算出关于s*的后验分布p(s*|t*,y,t,r,r*):

p(s*|t*,y,t,r,r*)～N(μ*,σ2)

(8)

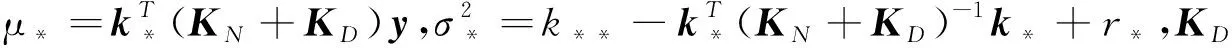
对r和r*进行积分，得到y*的后验分布：

(9)

由于无法直接求解式(9)，因此采用变分推断求取近似解。首先对边缘概率p(y)的对数进行分解，如式(10)。当寻求分布q(s)和q(r)最大化下界时，也就会使式(10)中KL散度最小化。优化p(s,r|y)在分解形式q(s)q(r)关于q(s)最大化的推导结论，可以进一步得到一个依赖于q(r)的近似下界，如式(11)所示。

ln(p(y))=L(q(s),q(r))+KL(q(s)

q(r)‖p(s,r|y))

(10)

式中，KL(·‖·)表示KL散度(Kullback-Leibler divergence)，L(q(s),q(r))是ln(p(y))的下界。根据式(11)的极值点与偏导数的关系，可得到μq和Σq，如式(12)和式(13)所示。

(11)

(12)

(13)

式中，tr(·)表示矩阵的迹，R为一对角矩阵，其对角元素为[R]ii=exp([μq]i-[Σq]ii)，而Kr是使用协方差函数kr(t,t′)计算的协方差矩阵,Λ表示半正定对角矩阵。

采用共轭梯度法优化参数高斯过程协方差函数中的参数、矩阵Λ中的对角线元素以及用于控制偏差项方差平均水平的μr，进而得到s*的后验分布：

(14)

基于以上结果，可以得到y*的后验分布(Lzaro-Gredilla et al.,2011;严宏等，2018)：

(15)

2 大坝变形预测模型构建

2.1 预测模型构建

(16)

图1 基于HGP的大坝变形预测方法建模流程Fig.1 Modeling flow of dam deformation prediction method based on HGP

2.2 工程实例

以丰满大坝为例，验证大坝变形预测HGP模型的有效性及可靠性。丰满水电站是中国最早建成的大型水电站,东北电网骨干电站之一，位于吉林省吉林市第二松花江的中游，吉林市东南为24 km处。拦江大坝为钢筋混凝土重力坝，坝长为1 080 m，坝高为91 m，水库正常蓄水位标高为263.5 m，库容为108亿m3。坝体从左岸到右岸共分60个坝段，每个坝段长为18 m。本研究选取30号坝段变形数据开展变形预测模型研究，收集了大约3年的大坝变形监测数据，包括大坝变形量γ(mm)、气温T(℃)、上游水位H(m)和累积时间t(d)数据。顾冲时等(2016)、吴中如(2003)、陈俊风等(2020)、王晓玲等(2020)较好地分析了丰满大坝和类似大坝的变形影响因子，在此基础上确定丰满大坝变形的影响因子包括11个，其中4个与水位有关的影响因子H、H2、H3、H4，5个温度有关的因子T、sin(2πt/365)、cos(2πt/365)、sin(4πt/365)、cos(4πt/365)，2个时间效应影响因子θ=0.01t、lnθ。将11个大坝变形影响因子作为HGP算法的输入，对应变形量作为输出。总共收集了164期变形数据，其中前129期数据作为训练数据集，用于确定HGP算法的超参数，进而建立变形预测模型(表1)；后35期数据作为测试集，用于分析预测模型的精密度及可靠性(表2)。

表1 训练集中的部分数据

表2 测试数据集

近年来，反向传播(BP)神经网络算法、最小二乘支持向量机(LS-SVM)和标准GP在变形预测领域得到较好的应用。为了进一步验证HGP算法具有更好的大坝变形预测精度，分别利用标准的GP算法(采用与HGP相同的核函数)、BP神经网络算法和LS-SVM算法构建大坝变形预测模型。分别对测试集进行预测(表3)。

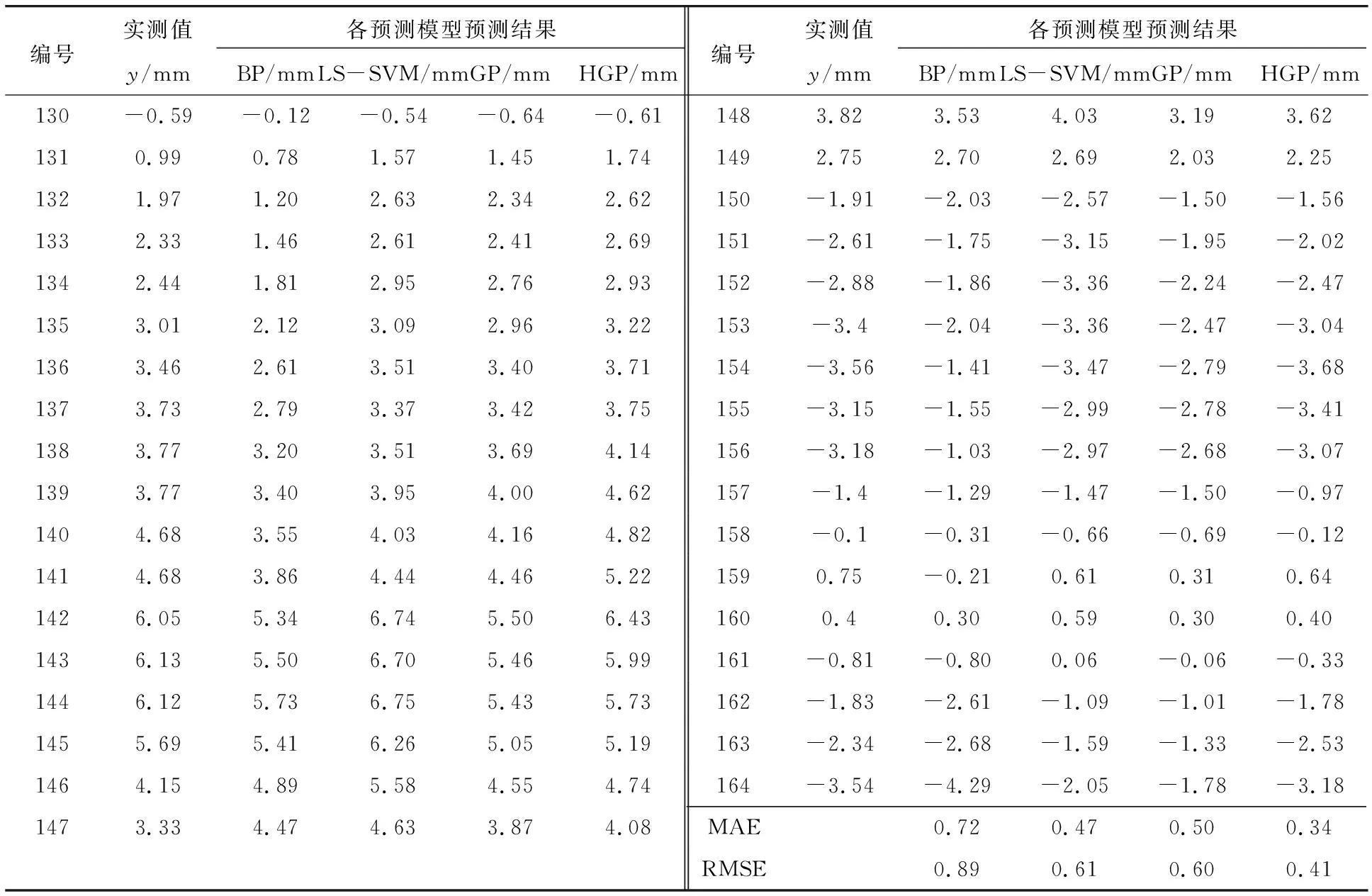
表3 变形预测结果

为了定量评价各预测模型的精度，采用平均绝对误差(MAE)和均方根误差(RMSE)评价各模型的精度，具体计算见式(17)和式(18)。根据各模型的预测结果，分别统计各模型的精度指标MAE和RMSE(表3)。由表3中的4种变形预测方法的精度指标可知，HGP算法的平均绝对误差和均方根误差均小于BP、LS-SVM和GP算法，验证了HGP算法具有更好的大坝变形预测精度。HGP算法的预测精度优于标准GP算法，表明HGP算法在标准GP的基础上，充分考虑了数据噪声变化的特点，有效改善了标准GP算法的大坝变形预测精度。

(17)

(18)