基于BP神经网络的海表温度预测

曾祥海，陈祥毅，陈文轩，邓颖欣，王观承

（广东海洋大学科技楼，广东湛江，524088）

0 引言

近年来，全球极端天气频发，人类的生存迎来极大的挑战，而作为地球气候系统重要成员的海洋，是一个对全球异常气候生成有着不容忽视作用的角色[1]。在海洋研究领域，水体表面的温度成为一个重要的研究方向。海洋表面温度（Sea Surface Temperature,SST），是台风路径、海洋生态系统的重要影响因素，是海气热量、动力、水汽交换的重要参量，更是衡量全球气候的重要地理参数之一[2]。在许多领域，如降水量预测、气温变化、干旱特征[3～5]等方面研究中，海表温度为开展此类研究的一种重要参量。掌握未来海表温度变化趋势有助于推动全球气候变化研究的开展，高效准确地获取未来海表温度信息对我国的海洋科研发展有积极的战略意义。在海表温度预测领域，前人采用数值预报法，经验预报法，统计预报法等预测海表温度[6～9]，然而传统的预测方法具有计算复杂度高，非线性数据预测效果差的缺点，且海水成分复杂，海表温度的影响因子繁多[10]，海表温度时间序列并非简单的线性关系，传统的数值分析法难以精准的预测海表温度。

随着神经网络算法的发展，神经网络的引入使得预测工作变得精准而高效。2015年，陈志宝等建立RBF神经网络预测模型，在光伏功率超短期预测中，相比无图像信息的模型预测效果明显提高[11]。2020年，周红标等提出AFNNMPC预测模型，在该模型中，AFNN在离线建模阶段利用学习算法改进网络参数，在实时控制阶段根据误差调整网络参数，为MPC取得优越的预测精度[12]。此外，在2021年，Wang等[13]利用多正弦函数分解神经网络 (MSFDNN) 分析中国南海北部湾及其邻近海域的有效波高，能有效地进行预测。同年，张雪薇等[14]利用ConvGRU深度学习网络模型预测海表温度，该模型结合了循环神经网络（RNN）与卷积神经网络（CNN）算法，取得较好的预测效果。在海表温度预测工作中，利用神经网络预测的方法并不多见，张莹等[15]使用EEMD和ARIMA算法预测海表温度，原理为利用EEMD算法对海温数据分解成多频率序列，再使用ARIMA模型对多频率序列进行逐一预测，最后将预测结果组合分析出未来海表温度数据。贺琪等[16]基于EMD-GRU模型对海表温度进行预测，相比较为常见的预测模型循环神经网络RNN和长短期记忆模型（LSTM）预测精度有所提高，原理为利用波分解算法对海表温度时间序列分解成较平稳的子序列，再将子序列通过GRU训练得到预测结果。近年来，BP神经网络已经广泛应用于各种领域，但在海表温度预测方面却并未涉及。基于海表温度数据非线性的特点，本文提出一种使用反向传播神经网络算法对海表温度进行预测，并对我国南海部分海域月平均海表温度进行验证分析。BP神经网络工作原理为通过梯度下降法不断修正权值和阈值大小，寻找权值与阈值最优解[17]。其隐层结构使之具备了良好的非线性求解能力，本文介绍了BP神经网络及其海表温度预测模型，其次进行预测分析，结果表明BP神经网络在预测海表温度方面具有实用价值。

1 BP神经网络基本结构

1.1 BP神经网络介绍与原理

BP神经网络是一种误差反向传播的多层神经网络，由科学家Rumelhart和McClelland于1986年提出的具有学习能力的一种人工神经网络[18]。人类的大脑皮层中有上百亿的神经细胞，即神经元，它主要由细胞体、突触、轴突和树突组成其工作原理是生物神经元树突接收外界信号，经过细胞体，随后由轴突传出。前一个神经元的轴突末梢与其他神经元的树突在突触的连接作用下进行信号连接，相互配合完成信息的交换。人工神经网络是一种拟生物单元，通过模仿生物脑神经网络的结构与功能，进行复杂的信息处理的数学模型。如图1所示，三层基本的BP神经网络拓扑结构，其中输入层与输出层称为可见层，其他中间层称为隐含层。人工神经网络与人类的神经元工作原理相类似[19]，不同的生物神经元中的突触具有不同的性质与强度，使得不同的输入信号产生不同的激励作用，在人工神经元中，对于每个不同的输入都具有一个可修正的权重，用于模仿生物神经元中突触的不同的性质与强度。在生物神经元中，膜电位没有超过动作电位的阈值时，生物神经元不产生神经冲动，为防止人工神经元输出为零的情况增加了偏置值。隐含层可将输入的数据特征线性划分不同类型的数据，使网络具有良好的自适应能力与分类识别能力。

1.2 BP算法基本步骤

三层神经网络基本拓扑结构如图1所示，第一层nx为输入层，第二层ke为隐含层，第三层ˆo为输出层，为了防止出现输出为零的特殊情况设置了偏置b。ˆo为网络预测值，o为真实值。BP神经网络算法可分为两步骤进行，分别为前向传递和反向误差传递。

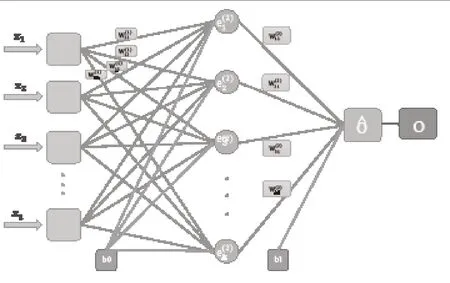
图1 三层神经网络基本结构

1.2.1 前向传递

三层神经网络BP算法在前向传递的过程中[20]，网络结构对应的计算流程如下：

对于隐含层有：

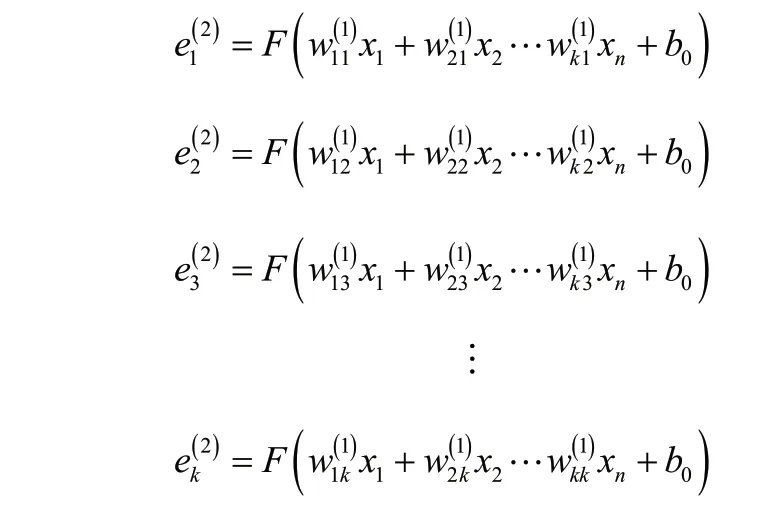
对于输出层有：

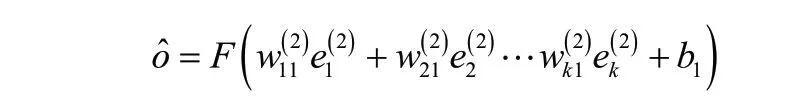
上述式子中，F(·)为非线性的激活函数，是网络模型重要的组成部分。非线性激活函数可以使得神经网络拟合各种复杂的非线性映射关系，因此该激活函数选择为非线性，实质上与傅里叶级数与泰勒级数相类似。另外，如果神经元的输出值极大时，未经处理传送至下一层神经元需要极大的算力，所以非线性激活函数将神经网络的输出值压缩到有界的区域内，对模型运算效率的提高至关重要。

Sigmoid激活函数、双曲正切Tansig激活函数、Relu激活函数和 Softmax激活函数是神经网络中常用的非线性激活函数，本文采用Tansig函数（1）作为神经元的激活函数。

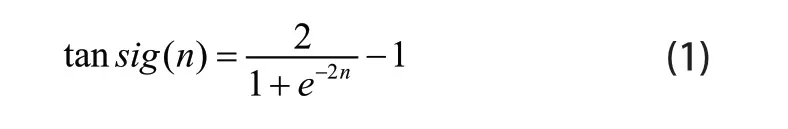
1.2.2 反向误差传递

在正向传播过程中，基于给定的初始化权重值w和偏置项b得出输出序列ˆo，若网络输出值不符合设定要求值，存在损失函数E，定义如下：

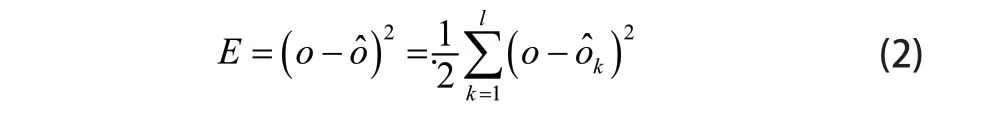
将损失函数E展开至隐含层：

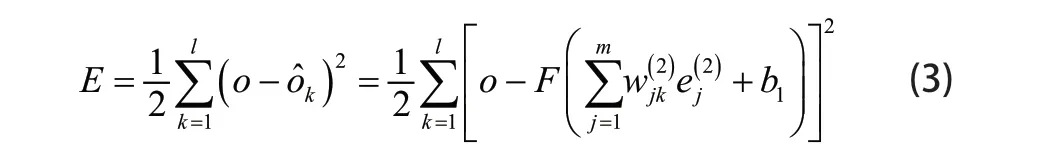
将（3）式再进一步展开至输入层：

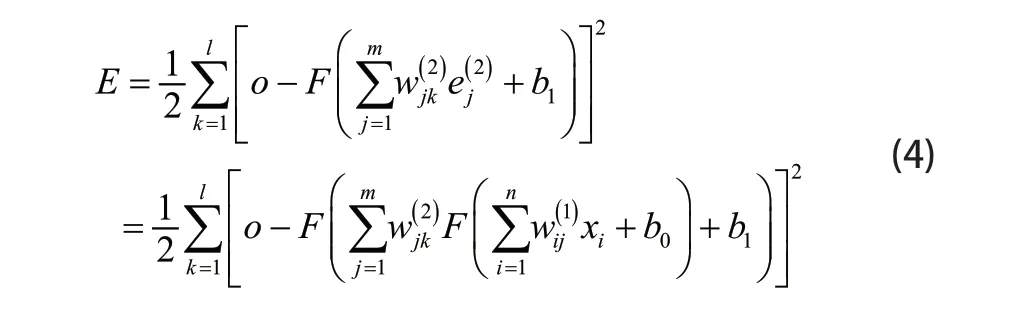
（2）～（4）式中，l为输出层节点数，m为隐含层节点数，n为输入层节点数。由（4）式可知，损失函数E是关于神经网络各层的权重值w得函数，由此，只需调整层与层之间的权重值即可改变损失函数E。显然，神经网络在调整权重时，原则上是使损失值E不断减小，采用梯度下降法，则权重的修正值为：

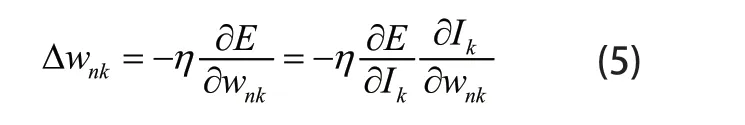
（5）式中:nkw为输入单元n到隐含层单元k的权重；η是学习速率，一般选取为0.01至0.8，kI是第k个隐含层的传输函数。

1.3 确定隐含层节点数

在网络过程中，输入层节点与输出层节点数目往往是已经确定的，输入层的节点数目与待定处理数据中输入的变量数目，输出层的节点的数目与全部输入相关联的输出的数目，但难以确定合适的隐含层节点数。隐含层节点数会影响神经网络模型的性能，过少则会使网络迭代的次数较多，训练的精度也会不高，从而导致学习能力不足。过多则会可能导致被训练的数据中包含的信息量过少，不足以训练隐含层中的神经元，从而导致出现过拟合的现象，易陷入局部极小值，难以达到预期的效果。显而易见，隐含层节点数的确定是一个至关重要的问题。因此，本文选择利用经验公式确定隐含层节点数：

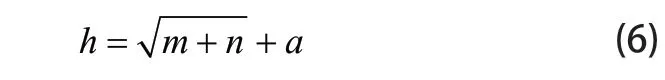
（6）式中，m为输入层个数，n为输出层个数，a为1～10之间的为常数。

2 数据收集与处理

本文所采用的海表温度数据为水平分辨率为1x 1的经纬度全局网格(360×180)的1891年1月至2021年11月的月平均海表温度数据，数据来源于美国国家海洋和大气管理局(NOAA)，数据下载网站为:https://psl.noaa.gov/data/gridded/data.cobe.html。本文基于月平均海表温度进行预测，为排除海表温度采集时因仪器故障或数据错误采集带来的误差，预测工作前本文使用孤立森林算法剔除原始数据的异常值点以减小训练误差，并将海洋表面温度序列延时12个单位(即一年)作为网络模型输入层参数。使用BP神经网络对海表温度数据的预测过程可以分为三步，首先将1891年1月至1983年9月的月平均海表温度历史数据用于训练。模型的参数训练完成后，将1983年9月至2021年11月作为测试集验证模型准确性。最后，基于2020年11月至2021年11月数据预测未来一个月海表温度数据，再以此数据迭代入网络输入层中，并使用最新的12个月数据预测下一个月数据，直至预测出未来12个月的海表温度后停止迭代更新。

3 海表温度预测误差分析

3.1 模型训练评价

在样本训练过程中，使用平均绝对误差MAE、平均绝对百分比误差MAPE和均方根误差RMSE作为误差分析特征指标。具体的计算公式如下：

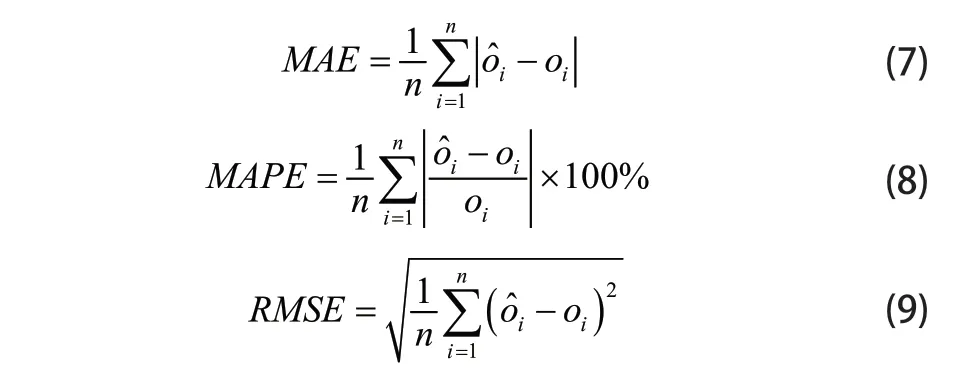
（7）～（9）式中，取值范围都为[0,+∞)，平均绝对误差MAE能够很好地反映预测值误差的实际情况，误差越大，MAE值越大。平均绝对百分比误差MAPE是一个百分比值，当MAPE为0%时，表示完美模型，当MAPE 大于 100 %时，则表示劣质模型。平均绝对百分比误差MAPE与均方根误差RMSE相类似，相比RMSE，为了消除个别离群点带来的影响，MAPE将每个点的误差值进行了归一化处理。 通过对误差的计算，分别得出上述三个评价指标，其中平均绝对误差为0.31203，平均绝对百分比误差为0.018272，均方根误差为0.39655，表明预测模型拥有较好的精确度。从表1与图3可以看出，预测值与真实海表温度较为接近，BP预测值和实际值之间平均误差仅为0.0565。

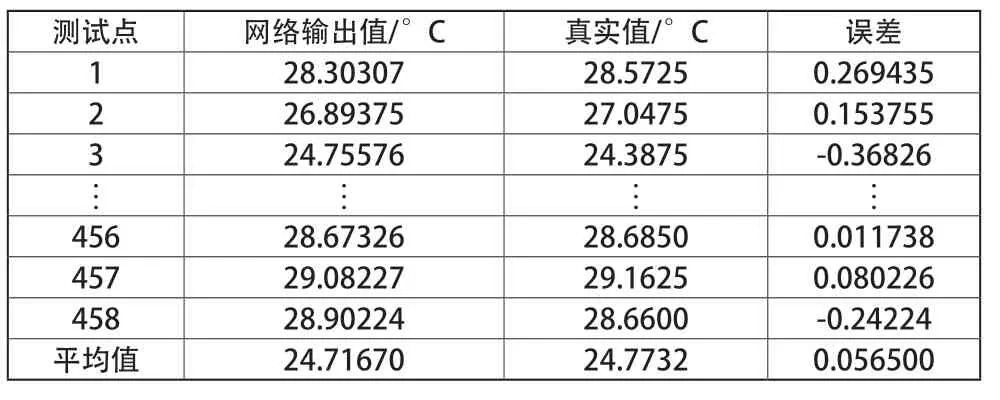
表1 测试集误差

图2表示了测试样本输出回归直线，纵轴Y为BP神经网络输出值，横轴X为真实海表温度数据，由图可知，回归直线的相关系数R=0.9767，与直线Y=X基本重合，可见，经过网络迭代训练后的目标输出值与海表温度真实值误差微小，表明BP神经网络是有效的预测方法。

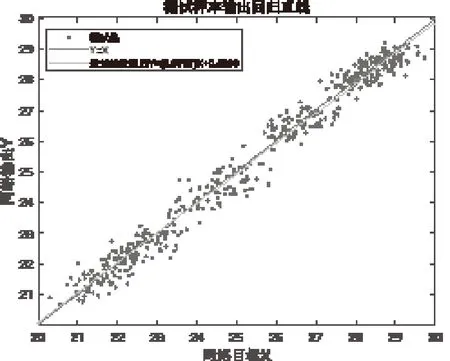
图2 测试样本输出回归直线

3.2 BP神经网络海表温度预测结果

将1983年9月至2021年11月某海域海表温度的实际值与BP神经网络所计算的预测值对比，可见BP神经网络预测值与实际值的结果匹配度较高，总体变化趋势基本一致，如图3所示。在实验最后，预测出未来12月海表温度数据，如图3及表2所示。

图3 海表温度的计算值、真实值和未来预测值图

4 结论与展望

随着科技发展，海表温度预测算法标新立异，但预测精准度仍然有待提高。本文用BP神经网络对海表温度进行预测，基于1891年1月到2021年11月的月平均海表温度数据对BP神经网络 模型进行预测和验证，并对未来一年海表温度进行预测，研究得出结论：BP神经网络的输出预测值与真实值偏差极小，平均误差仅为0.057，结果匹配度较高，总体变化趋势基本一致，用于海表温度预测可行且有效。通过研究已有海温相关数据预测出海温在未来一段时间内的变化趋势，进而根据预测所得的结果合理规划生产活动，同时也为环境部门提供参考，从而制定出有效的环境保护政策。本次研究中可用的数据仅仅是海表温度数据，然而引起海表温度变化的重要影响因子众多，例如地理位置、南方涛动指数、海表盐度、海表风场等，在后续的研究中可以对模型进行优化，结合更多的特征，提高海表温度预测的准确度。