一种面向空天飞机再入的智能自适应复合控制方法

周大鹏，杨大鹏，刘 然，周云龙

(1. 沈阳飞机设计研究所，沈阳 110035; 2. 北京航空航天大学 航空科学与工程学院，北京 100191)

0 引 言

空天飞机执行任务时会经历由稀薄大气到稠密大气的飞行过程，此时气动舵面的控制效率变化强烈，需要引入直接反作用力控制系统(Reaction control system, RCS)辅助气动舵面进行姿态控制。同时再入过程中飞行器也面临着横侧向通道强耦合、气动参数快时变的问题，使得空天飞机横侧向通道的再入姿态复合控制设计面临着许多困难。

针对再入姿态复合控制问题，常规单一的线性控制方法无法有效地解决，由此引出一系列再入控制方法的改进。文献[2]提出了一种基于LQR和自抗扰控制的再入姿态控制方法，采用LQR方法完成状态反馈控制律设计，然后结合自抗扰技术设计扩张状态观测器对系统不确定性和外部干扰进行补偿。文献[3]结合Ⅱ型模糊神经结构和误差反馈学习架构设计了一种在线自主学习干扰观测器，然后提出了基于该干扰观测器的超螺旋滑模控制器，实现再入姿态跟踪。文献[4]提出了一种基于模糊扰动观测器的预测滑模控制方法，该方法用于估计包含系统不确定性和外部扰动的复合扰动。文献[5]将再入飞行器的姿态控制建模为非线性系统的最优控制问题，提出单网络积分型强化学习算法进行求解，该方法计算效率高、收敛速度快，给智能方法在再入姿态控制中的运用提供了一种思路。此外，再入姿态复合控制还需要重点关注控制框架问题，文献[6]采用了一种直接力、气动力的单一切换框架，在直/气系统均稳定的情况下，分别设计对应的控制方法，然后给定了两系统的调整逻辑。但是异类执行系统独立设计的方法无法充分发挥复合控制系统的性能，因此目前多数学者的工作集中于并联工作的复合控制框架，如文献[7]在考虑舵面位置和速度约束的基础上，面向各执行机构设计了一种基于线性规划控制分配的复合控制框架；文献[8]设计了一种并联结构的多级复合控制框架，直/气数学舵采用链式复合控制，下一级气动物理舵则采用优化复合控制方法。

针对再入控制分配问题，即气动舵面和RCS机构之间的调配策略问题，文献[9]提出了一种链式分配策略，这属于非优化分配方法，思想就是先用气动舵面进行控制，当气动舵的能力不够的时候开始调用RCS进行控制，该方法简单有效，但是自调节能力弱；文献[10]提出了一种多级分配策略：气动舵面和RCS之间的分配方式采用简单的动压比例分配法；气动舵面之间的次级分配采用最优二次规划法；而RCS系统之间的次级分配采用混合线性整数规划法，该多级分配策略能够实现控制指令由总到支的完整分配。文献[11]重点考虑气动舵面和RCS之间的控制分配问题，基于最优二次规划算法，提出了一种改进的分配指标，根据姿态控制需求实时更新二次规划算法的权重，实现了控制需求和能量消耗的权衡。

本文重点研究空天飞机横侧向通道的姿态复合控制问题。首先，建立了空天飞机横侧向通道的动力学模型，在常规飞行器动力学方程的基础上引入RCS力矩项。然后，提出了一种神经网络PID控制算法，在全量PID控制律基础上引入神经网络控制补偿模块，通过网络权重的在线迭代实现控制指令的实时补偿。同时，针对再入过程横侧向通道的强耦合特性，在基线PID控制律中引入交叉耦合系数，将实际侧滑角反馈至横向通道控制律中，实现横侧向通道的耦合控制。最后，建立了一种自适应链式分配方法，结合迭代最小二乘气动参数辨识方法对再入飞行舵效进行实时估计，进而输入进链式分配律中，在线更新分配策略，以提高飞行环境适配能力。

1 空天飞机再入横侧向动力学模型

空天飞机同时具有气动舵面和RCS两类异构执行系统，因此在建立空天飞机动力学模型时需要考虑RCS系统的作用。本文重点研究横侧向通道的再入姿态复合控制，因此这里只建立横侧向双通道的动力学模型。参考文献[12-14]，建立空天飞机横侧向动力学模型如下所示：

(1)

2 空天飞机再入横侧向神经网络PID控制律设计

神经网络PID控制律由BP神经网络和常规PID控制律组成。常规全量式PID控制律作为基线控制律，而BP神经网络输出控制增量，对PID控制律的控制指令进行修正。空天飞机横侧向通道的神经网络PID控制流程图如图1所示：

图1 空天飞机再入横侧向神经网络PID控制流程图Fig.1 Flow chart of the neural network PID control for the reentry roll and yaw channels of aerospace plane

图1中,,和分别为空天飞机再入姿态指令、空天飞机再入实际姿态值和姿态跟踪误差；为全量PID控制律输出的控制指令；Δ为神经网络模块输出的补偿控制指令；,和为神经网络模块输出的PID补偿参数。

2.1 面向横侧向再入控制的神经网络结构设计

分别针对横向通道和侧向通道设计BP神经网络结构。单通道内，采用3层前向神经网络结构，其中包含网络输入层、网络隐含层和网络输出层。在单通道神经网络结构中，可以根据控制目标确定网络输入层和网络输出层的神经元个数。

横向通道中，网络输入层由3个神经元组成，分别对应于再入倾侧角指令，实际倾侧角值，以及倾侧角跟踪误差；网络输出层由3个神经元组成，分别对应于PID的三个控制参数：P,I和D。

侧向通道同理，网络输入层的三个神经元分别对应于再入侧滑角指令，实际侧滑角值，以及倾侧角跟踪误差；网络输出层的3个神经元分别对应于PID的三个控制参数：P,I和D。

将网络输入层的3个神经元概称为,和；将网络输出层的3个神经元概称为,和。那么面向PID控制的神经网络可以设计为图2所示的结构：

图2 神经网络结构示意图Fig.2 Schematic diagram of the neural network structure

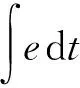
2.2 神经网络正向传播计算方法

正向传播，即将样本输入进神经网络，然后经过网络输入层、隐含层和输出层，最后获得网络输出的过程。面向再入飞行器横侧向通道控制的神经网络正向传播计算方法在横向通道和纵向通道中是一致的，因此这里采用统一的相关符号进行单通道神经网络的描述。

1) 网络输入层

规定网络输入层的输入量和输出量是一致的，即有如下数学关系：

()=()=[(),(),()]

(2)

式中：为任意采样时刻对应的仿真步长，这里描述成离散的形式，以方便后续编写程序。上述方程中的()是第步输入层的输出向量，()是第步输入层的输入向量，维数3×1；()是第步的角度标称值；()是第步的实际角度值；()是第步的角度跟踪误差；在神经网络的具体设计过程中，横侧向通道是独立进行的，因此在单通道神经网络中，(),()和()均为标量。

2) 网络隐含层

网络输入层的输出向量经过权重矩阵之后即网络隐含层的输入量，该输入量经过隐含层的激活函数便可以得到隐含层的输出量，描述为数学形式：

(3)

(4)

3) 网络输出层

网络隐含层的输出向量经过权重矩阵之后即网络输出层的输入量，该输入量经过输出层的激活函数便可以得到输出层的输出量，即神经网络的最终输出量。描述为数学形式：

(5)

式中：()是第步输出层的输出，()是第步输出层的输入，维数规定为3×1；()为隐含层输出转为输出层输入的权重矩阵，维数为3×；(·)为输出层的激活函数，规定为Sigmoid函数，表达式为：

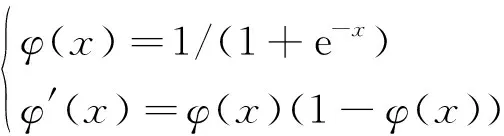
(6)

空天飞机再入横侧向通道姿态控制过程中，采用在线神经网络权值更新方法，第步的(),()和()输入进神经网络网络，经过第步网络权重(),()的运算，输出第步的修正控制量Δ()，然后经过被控对象动力学模型后得到第+1步的状态量(+1)。这时需要计算(+1)与(+1)之间的误差，进而根据一定的准则对(),()进行修正，得到(+1),(+1)。

BP算法就是一种更新网络权重矩阵的准则，其根据网络输出层的输出与参考值之间的误差，对网络中的权重矩阵进行修正，从而使得网络的输出与参考值之间的误差越来越小。下面结合空天飞机再入横侧通道姿态控制的背景，具体推导网络权重矩阵的更新过程。

2.3 神经网络隐含层至输出层权重矩阵更新算法

在推导权重矩阵的更新算法之前，首先需要建立损失函数用以描述空天飞机再入的实际角度值和标称值之间的接近程度：

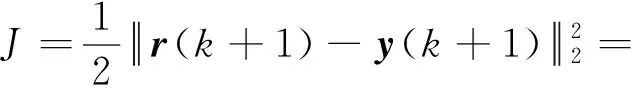
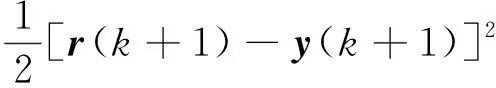
(7)

神经网络权重矩阵的更新要以损失函数达到最小为导向，使空天飞机再入的实际角度值和标称值之间的误差达到最小。将姿态跟踪误差的二范数作为损失函数，误差导向权重矩阵的更新，从而产生新的控制指令分配到直/气复合控制系统中，实现跟踪误差的快速减小。

权重矩阵的BP更新算法为反向的，因此首先需要更新隐含层至输出层的权重矩阵：

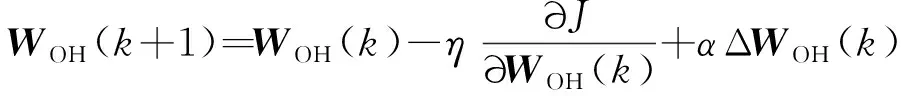
(8)

式中：采取的是改进型的寻优下降方向来寻求损失函数的最小值，标准型为负梯度方向，即-∂∂()；为学习速率；这里增加了最后一项动量项，为惯性系数；Δ()为第步的权重矩阵修正量。

采用基于最速下降方法的权重矩阵更新方式，可以快速收敛到最优解。同时引入动量因子，增加权重更新的阻尼，减小了振荡趋势。

由式(8)知，第+1步(当前步)的权重矩阵修正量为：

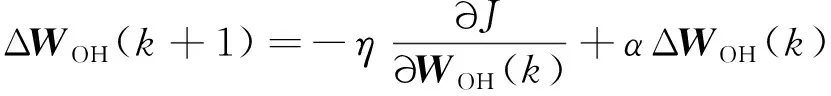
(9)

式中：∂∂()是未知的，下面采用链式法则推导∂∂()的表达式：

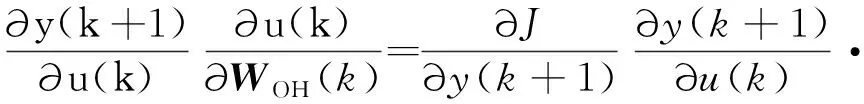
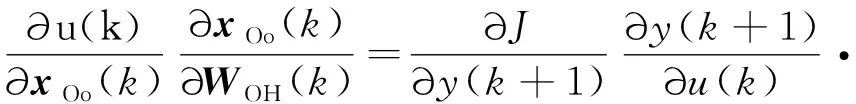
(10)

式中：

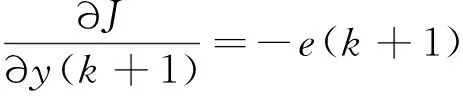
(11)

(12)

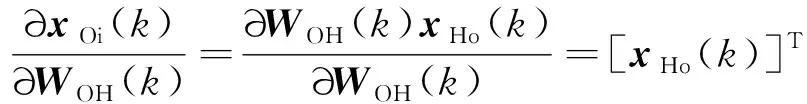
(13)

上述推导过程中，为了描述的简便，将修正控制量Δ()简写为了()，其依然表示修正控制量，而不是基线PID控制律所输出的主控制量。在神经网络中，修正控制量()可以写为：

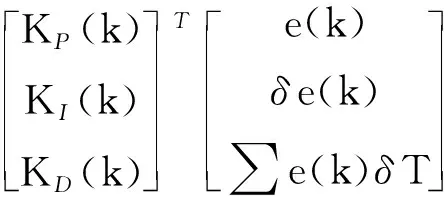
(14)

式中：(), δ()和∑()δ分别表示第步的角度跟踪偏差、偏差的微分项以及偏差的积分项；为仿真采样周期。那么式(10)中的∂()∂()可以写为：

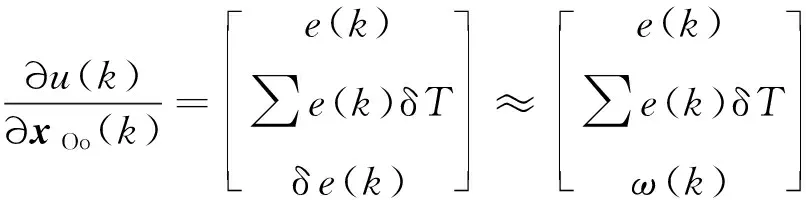
(15)

式中：()为第步的角速率，即用空天飞机再入过程的角速率近似代替被控角度的微分量。

针对∂(+1)∂()，难以写出解析式，因此这里用符号函数表示，即

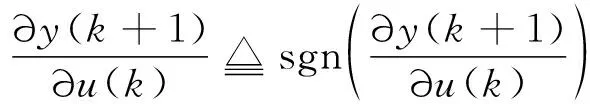
(16)

对于正常布局的飞行器来说，如果控制量()是舵偏，则sgn(∂(+1)∂())=-1恒成立；如果控制量()是力矩，则sgn(∂(+1)∂())=1恒成立。由符号函数代替∂(+1)∂()产生的偏差由学习速率和惯性系数进行补偿。

综上所述，式(10)可以改写为：

(17)

最终得到的∂∂()是一个3×维的矩阵，为隐含层的神经元个数。

那么，式(9)所示的权重矩阵修正量Δ就可以改写为：

Δ(+1)=η[()]+Δ()

(18)

2.4 神经网络输入层至隐含层权重矩阵更新算法

更新完成输出层权重矩阵()后，还需要更新输入层至隐藏层的权重矩阵()。在BP神经网络中，各层权重矩阵的更新之间是存在一定的递推关系的，下面先把该递推关系推导出来。

在上述2.3节中建立了∂∂()的链式展开式(10)。同时，其还可以展开为以下不同的形式：

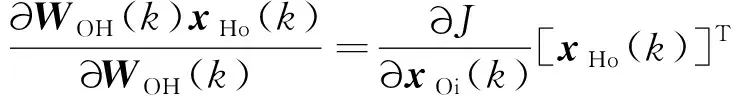
(19)

对比式(18)发现，存在以下关系式：

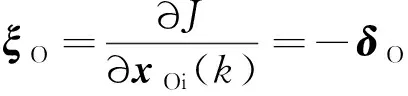
(20)

下文建立和之间的关系，求出后，类比式(19)，自然便可得到∂∂()。

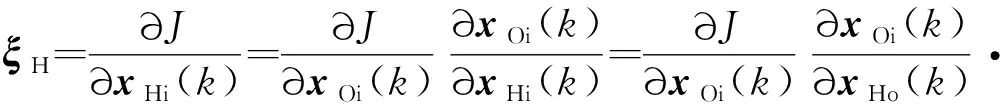
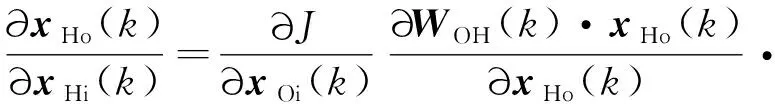
(21)

其中,求解得到的是一个×1的向量。

类比式(19)，可以得到如下关系：

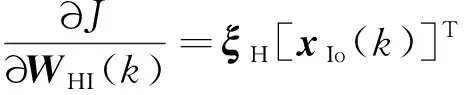
(22)

其中,得到的∂∂()是一个×3维的矩阵。

所以，第+1步的输入层至隐含层的权重矩阵修正量Δ可以写为：

Δ(+1)=-η[()]+Δ()=

η[()]+Δ()

(23)

2.5 空天飞机再入横侧向耦合控制方法

文献[8]，在滚转通道中引入交叉耦合反馈项进行姿态控制增稳，通过侧滑角在横向通道的反馈，加快对因转弯指令突变而产生的控制超调的抑制，提高侧滑角和倾侧角的控制稳定性，弱化两者之间的控制干扰：

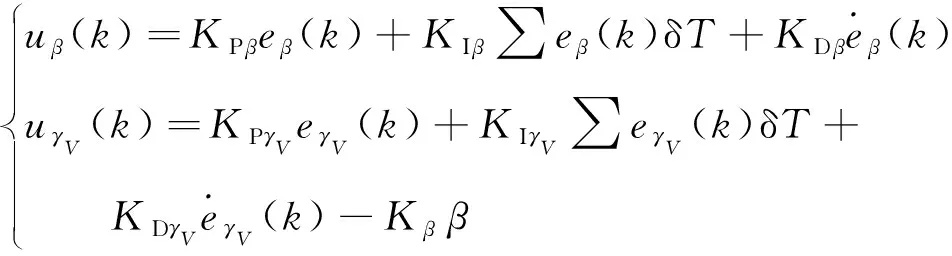
(24)

这种耦合控制结构实际应用在基线PID控制律中。式(24)就是常规的全量式PID控制律，然后引入了交叉耦合反馈系数。其中δ表示单位采样周期。

3 基于实时气动辨识的自适应链式分配律设计

空天飞机同时具有气动舵面和反作用控制系统RCS两类异构执行机构，这是因为当空天飞机处于稀薄大气层时，大气密度低，气动舵面无法有效完成控制指令，RCS系统作为辅助控制装置被引入。当空天飞机经历大气层由稀薄变为稠密的飞行过渡阶段时，气动舵面和RCS系统均需要参与姿态控制，因此需要按照一定的准则调配这两类异构执行机构进行复合控制。

3.1 基于实时气动辨识的链式分配律设计

第2节研究的空天飞机再入横侧向神经网络PID控制律最终求解出的控制指令为力矩指令：cmd和cmd。结合空天飞机再入的横侧向通道动力学模型(1)，规定控制指令到转动动力方程的传输有如下关系：

(25)

采用链式分配律将力矩控制指令进行分配，该方法的一般实施步骤为：首先利用气动舵面实现控制力矩指令；当控制力矩指令所需的控制能力超出气动舵面的实际能力时，开始调用RCS系统来完成剩余的控制任务。

设气动舵面的偏转范围为：[,]，且有<0,>0。那么上述链式分配算法便可以写为：

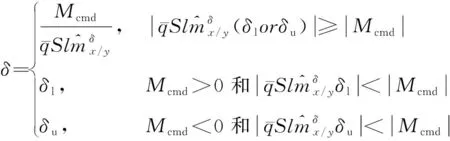
(26)

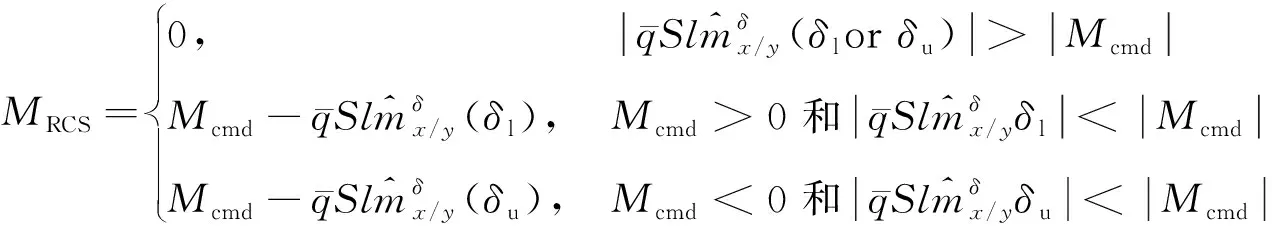
(27)

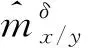
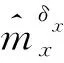
3.2 时域递推最小二乘辨识方法

由于空天飞机再入横侧向通道的气动模型存在差异，因此采用分通道辨识的方法。首先设定横向通道和侧向通道的气动力矩系数模型分别为：

(28)

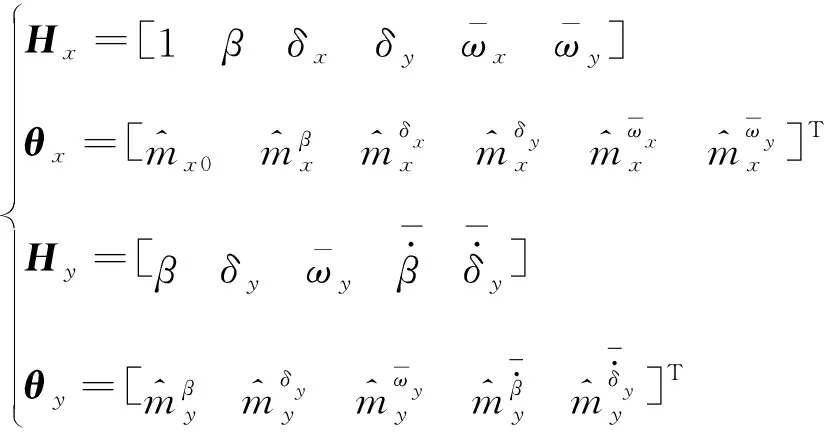
(29)

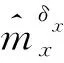
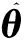
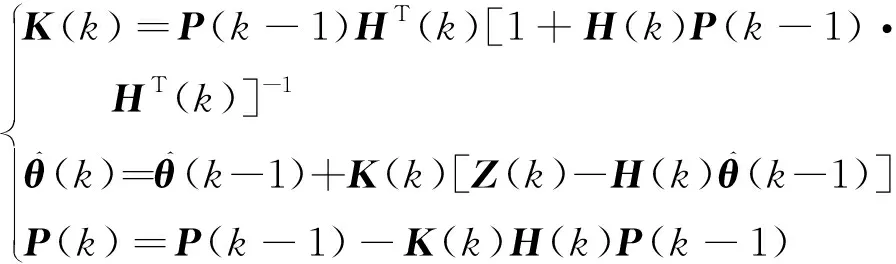
(30)

式中：()为第步的参数迭代比例矩阵；()为第步的辨识协方差矩阵；()是第步的观测值。

(31)

在气动辨识过程中，为了能够提高辨识精度，常常需要在控制输入环节加入一定的激励，从而激发出气动模型中各状态的特征，这里规定激励信号输入进舵面偏转量中。文献[20]，在舵偏量中加入正交优化多正弦激励信号：

(32)

式中：和分别为加在副翼和方向舵上的正交优化多正弦激励信号；和为横向通道和侧向通道多正弦激励信号的振幅；为相位角度；为可用谐波频率的总数；为激励时间段长度。

针对正交多正弦激励信号，定义一个相对峰值因子RPF：

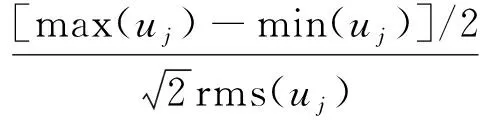
(33)

理想的RPF是具有较低值的，这是因为在激发再入飞机在各种频率具有良好的输入能量的同时最小化输入振幅，避免再入飞机远离参考飞行条件。对于单位振幅的单个正弦信号，无论频移或者相移，RPF均为1，那么多正弦输入的最优目标即使得RPF为1。

由于多正弦输入信号式(32)中的相位角的设定不会影响相互正交输入，因此可以调整相位角使得RPF值达到最优值1。

4 仿真校验

4.1 横侧向通道神经网络PID控制律仿真

选择空天飞机经历从稀薄大气到稠密大气的再入过渡飞行阶段作为仿真工况，这个过程中动压由极低的值开始逐渐增加，气动舵面逐渐恢复控制能力。

针对该仿真的飞行初始速度为7 km/s，飞行初始高度为103 km，此时给定滚转转弯方波指令，即倾侧角指令在±45°内方波变化，同时给定侧滑角指令恒为零，≡0°。然后在横侧向通道中校验本文中的神经网络PID控制律对姿态指令的控制跟踪效果。

搭建横侧向通道神经网络PID控制律的Simulink模型进行仿真。控制输出指令设置为力矩指令，相应的参数设置如表1所示：

表1 仿真参数表Table 1 Simulation parameters

对于权值矩阵的初值，横侧向通道均取为[0, 1] 区间内相应维度的一组随机值。为实现横侧向通道耦合控制而引入的交叉耦合系数取为=25×10。

仿真过程中，在滚转力矩和偏航力矩中加入-40%的常值拉偏以及+20%的三角函数时变拉偏，得到图3所示的再入过程中侧滑角和倾侧角的姿态跟踪控制曲线。

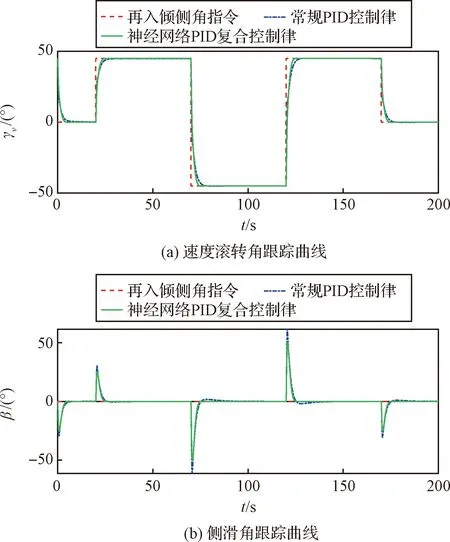
图3 横侧向通道姿态跟踪曲线Fig.3 Attitude tracking curves of roll and yaw channels

分析图3得知，再入过程中空天飞机进行大角度无侧滑横滚转弯时，本文采用的神经网络PID控制律相较于常规全量PID控制律具有更快的收敛时间，限制在5 s左右，以及更小的控制超调，侧滑角的峰值超调减小了10°以上。同时，在加入常值扰动和三角函数扰动后，神经网络PID控制律具有更好的鲁棒性表现。

在横侧向通道耦合神经网络PID控制仿真校验的过程中，控制分配模块采用的是上述推导的自适应链式分配方法，控制力矩的分配结果如图4和图5所示。

图4 横侧向通道复合控制力矩变化曲线Fig.4 Change curves of compound control moments in roll and yaw channels

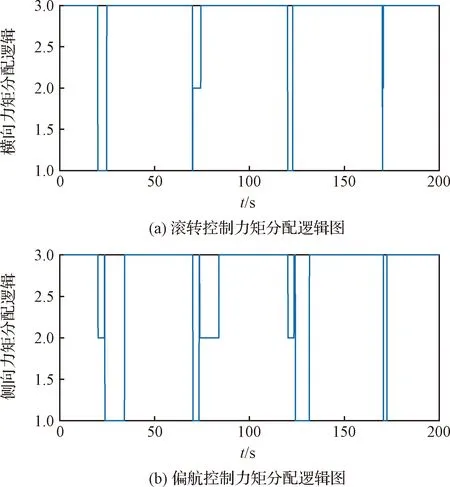
图5 横侧向通道控制力矩分配逻辑图Fig.5 Logic diagram of control moment allocation in roll and yaw channels

其中，图4是自适应链式分配律模块的控制力矩分配曲线，虚线是需用力矩指令，实线是气动力矩分量，点划线是RCS力矩分量。由该仿真图分析知，空天飞机再入过程中当需用力矩特别大的时候气动力矩无法提供，需要RCS力矩进行辅助控制，通过自适应链式分配律能够实现两者的合理调配；图5是需用力矩指令的分配逻辑图，纵轴“3”表示需用力矩在气动舵面控制能力范围内，纵轴“2”表示正向需用力矩超出气动舵面控制能力，纵轴“1”表示负向需用力矩超出气动舵面控制能力。

4.2 横侧向通道递推最小二乘气动辨识仿真

横侧向通道分别选择正交多正弦激励信号：

(34)

式中：多正弦激励信号的相对峰值因子RPF值为1.1936，的相对峰值因子RPF值为1.0027，均比较接近最优值1。

有了激励信号后，将在线气动辨识模块加入到空天飞机再入复合控制的自适应链式分配律中，实现链式分配律的在线调整。基于递推最小二乘方法的气动辨识结果如图6和图7所示：

图6 横向通道气动参数辨识结果Fig.6 Identification results of aerodynamic parameters in roll channel

图7 侧向通道气动参数辨识结果Fig.7 Identification results of aerodynamic parameters in yaw channel

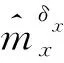
5 结 论

空天飞机在稀薄、稠密大气的临界飞行以及横侧向通道表现出的强耦合与快时变特征，使得其再入姿态控制变得困难。提出了一种神经网络PID控制律，以全量PID控制律为基线，引入神经网络控制补偿模块，根据姿控误差实时调整网络权重，输出补偿控制力矩。此外，面向异构执行机构提出了一种基于实时气动辨识的自适应链式分配方法，将在线获得的舵效辨识值输入进链式分配律中，实时更新分配策略。最后，仿真校验了方法的有效性，横侧向神经网络PID控制律提高了空天飞机再入横滚转弯时的姿态跟踪速度与精度，自适应链式分配律实现了在线策略调整，提高了空天飞机再入复合控制方法的多场景应用能力。

下一步工作中将重点改进智能神经网络复合控制律，实现神经网络控制模块脱离基线控制律的独立高效运行。此外，智能再入复合控制应不局限于控制律的智能化，随着数据驱动的学习算法的引入，下一步控制分配模块的智能化将会同步进行，提高智能再入复合控制系统的通用能力。