基于标准贯入试验的地基承载力特征值优化
2022-09-22唐国强李裴君朱满红
唐国强 李裴君 朱满红
(1.杭州市勘测设计研究院有限公司 浙江杭州 310012;2.西北综合勘察设计研究院 陕西西安 710000)
标准贯入试验常用来评估地基承载力的稳定性,诸多因素会对标贯试验结果造成干扰[1]。许多学者对标贯试验进行了研究:肖泽忠等[2]对桂林市红黏土地质的标贯试验进行分析,认为不同深度的土压力差异和钻杆因素直接影响地基承载力的计算精度;蒋志勇[3]对标准贯入试验的适用条件进行了研究,认为标贯试验锤击次数与黏性土的可塑和硬塑状态密切相关;王东觉等[4]基于标贯试验锤击数,对地基土单元进行了划分,确定了桩基础的极限阻力标准值;罗阳生[5]认为国内的标准贯入试验方法比较注重经验的应用,简单实用,而国外的计算方法较为繁琐,难以推广使用;宋二祥等[6]认为地基土的自重对地基土承载力具有重要影响,地基土重度对地基承载力作用可转换为粘聚力随深度的增长率;刘福臣等[7]对规范中的地基承载力可靠度进行了分析,认为规范中基于标贯试验确定地基承载力的保证率仅有50%。
虽然许多学者基于标贯试验对地基承载力进行了研究,但是基本上是对规范的直接运用,基于统计数据进行的地基承载力计算的保证率仅有50%。本文基于沁河供水管线穿越工程勘察资料,基于t分布的基本原理,对基于标贯试验进行地基承载力计算的方法进行了优化,以期为类似工程提供借鉴[8]。
1 标准贯入试验
《建筑地基基础设计规范》对标准贯入试验进行了详细的说明,其适用于砂土、粉土和一般性黏土等地质条件。进行标准贯入试验时,标准贯入孔宜采用回转钻进,孔内废土高度小于5cm,标贯孔内的水位略高于地下水位,贯入器不得冲击孔底。采用自由落锤法进行锤击时,在保证垂直度的前提下,还要使贯入器、探杆、导向杆间紧密相连。进行标贯锤击试验时,锤击速率不超过30 击/min,在贯入器打入土体15cm 后,开始记录每贯10cm 的锤击数,以累积贯入30cm 锤击数作为标贯锤击数。当累积已进行了50次锤击,而贯入深度还小于30cm 时,应终止试验,按照式(1),将其换算为标贯试验锤击数。

式中:ΔS为50 次锤击时的贯入深度(cm);N为标贯次数。
进行标准贯入试验时,受各种因素的影响,会使标贯试验成果与实际情况具有一定的误差,此时,应根据实际工况对标贯次数进行相应修正。《建筑地基基础设计规范》(GBJ 7-89)对标贯击数N(N10)的修正做了如下规定:

另外,目前现行规范中对标贯试验的修正主要有杆长修正和地下水修正。采用杆长修正时,对于饱和砂土中在地下水位以下的中、粗砂,其标贯击数应在实测击数上增加5击次;判断花岗岩的分化程度、黏性土的物理状态、砂土液化等应采用实测值;进行水运岩土勘察时,使用实测试验击数。
2 标贯试验的地基承载力计算
通过对大量标准贯入试验资料进行统计,《建筑地基基础设计规范》(GBJ 7-89)收录了砂土、黏性土的标准贯入击数与承载力特征值的对照表。砂土承载力特征值对照表如表1所示,黏性土承载力特征值对照表如表2所示。
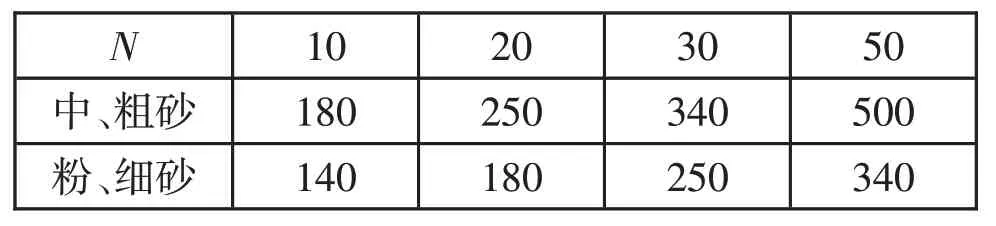
表1 砂土承载力特征值fck(单位:kPa)

表2 黏性土承载力特征值fck(单位:kPa)
为了增加标准贯入试验计算地基承载力特征值的适用性,分别对砂土地基承载力特征值对照表和黏性土地基承载力特征值对照表进行拟合运算,则可以得到如下内容。
中粗砂地基承载力特征值:
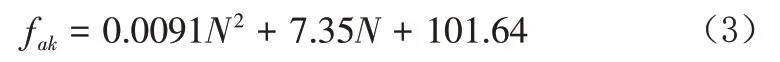
粉细砂地基承载力特征值:
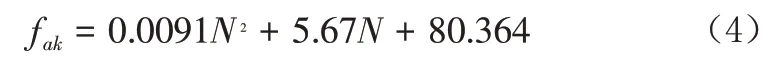
黏性土地基承载力特征值:

式(3)、式(4)、式(5)是对大量标准贯入试验进行统计得到的经验公式,由于实际试验受到多种因素的干扰,实测数据存在一定的离散性,由大数定律可知,上述经验公式的保证率仅有50%。
3 地基承载力特征值优化
3.1 t分布函数
受到多种因素的影响,标准贯入试验数据存在一定的离散性,并且服从某种分布。由统计学理论可知:正态分布适用于样本无限大且方差未知事件,t分布适用于样本空间有限且方差未知的事件。对于具体的标准贯入试验,可用t分布对地基承载力预测公式进行优化。
标准正态分布概率密度函数可表示为:
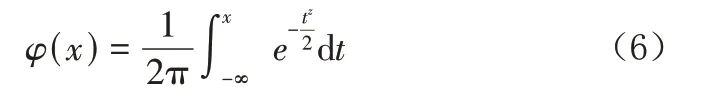
t分布的概率密度函数可表示为:
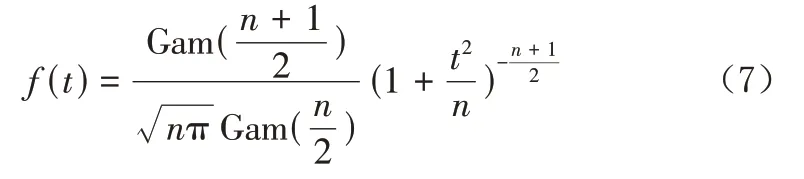
式中,Gam(x)为伽玛函数。
相对于标准正态分布,t分布引入了自由度(df)的概念,由标准正态分布与不同自由度t分布的曲线特征可知:当自由度由1 发展到31 时,t分布曲线的形态越来越接近标准正态分布;当自由度为31时,t分布曲线几乎与标准正态分布一致。所以,可以将t分布应用于样本数量有限的事件。
3.2 t分布变化
无限实测的标准贯入试验实测数据组成事件A,由统计学规律可知,事件A可用正态分布表示:

式中:μ为地基承载力期望值;σ2为地基承载力方差。
由事件A抽取n个样本组成事件B,由中心极限定理可知,n值越大,事件B的样本均值越接近正态分布。事件B可表示为:

事件B对应于现场实际的标贯试验,其实际标准差f未知,可用样本标准差S替代。其t分布变化可表示为:

式中,S为样本标准差,其他参数含义同上。
3.3 基于t分布的地基承载力优化计算
公式(10)满足n-1自由度的t分布,可记作:
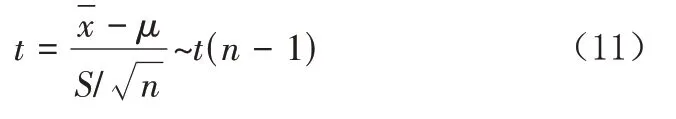
根据公式(11),结合实际试验的自由度,可以确定某事件的置信水平,其发生的置信概率为:
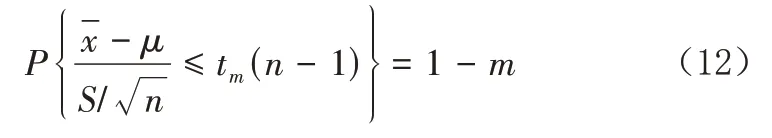
式中,1-m为置信水平。
假设某点位标贯试验地基承载力的置信概率为1-m,由式(3)、式(4)、式(5)和式(11)、式(12)可计算出不同地质条件下的修正地基承载力。

4 工程算例
4.1 工程概况
沁河供水管线穿越工程位于沁阳市东外环东侧约200m 处,张庄与南金村之间,北岸接点位置位于观门村与北金村之间,管线下穿主河槽位置距离上游S308公路桥约2.5km,距离下游长济高速沁河大桥约3.3km,穿越拟采用定向钻方案,穿越水平长约1.683km。根据钻探结果,结合区域地质条件,发现穿越场区地层主要由第四系冲洪积粉质黏土、中砂、粉细砂、卵石、粉质黏土组成。管道总体走向如图1所示。

图1 管道走向示意图
4.2 标贯点位布置
本工程中共布设8个标贯孔位,分别为ZK2、ZK3、ZK4、ZK5、ZK7、ZK9、ZK11、ZK14,除了ZK2 孔深为25m、ZK3孔深为40m外,其他孔深均为45m。标贯孔位布设平面图如图2所示,工程地质剖面图如图3所示。
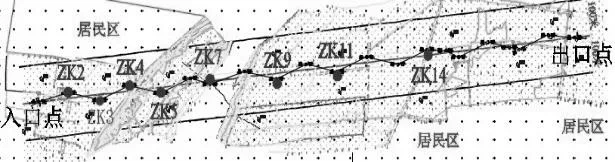
图2 标贯孔位布设示意图

图3 工程地质剖面示意图
4.3 标准贯入试验结果统计
对每个标准贯入孔进行不同深度的标贯试验,统计每次标贯试验的锤击数,并且根据实际情况对标贯试验锤击数进行修正。列举部分标贯试验结果如表3所示。

表3 标贯试验统计表
对以上统计数据进行t分布的自由度计算可知:中粗砂的自由度为19;粉细砂的自由度为5;黏性土的自由度为30。
4.4 基于t分布的地基承载力优化计算
基于式(3)、式(4)、式(5)可以分别求出中粗砂、粉细砂、黏性土的地基承载力特征值,对其进行数据处理,可以分别得到中粗砂的标准差为20.42、粉细砂的标准差为3.04、黏性土的标准差为21.24。
假定每次标贯试验的置信概率要大于99%,查t分布表可知,置信度为99%且自由度为19的置信区间上限单侧值为3.174;置信度为99%且自由度为5的置信区间上限单侧值为4.773;置信度为99%且自由度为30的置信区间上限单侧值为2.75。
则根据式(13)可以分别得到中粗砂、粉细砂、黏性土的地基承载力特征值优化计算公式。
中粗砂地基承载力特征值优化公式:

粉细砂地基承载力特征值优化公式:
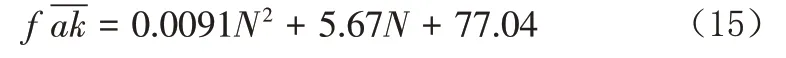
黏性土地基承载力特征值优化公式:

4.5 基于t分布的地基承载力评价
分别对地基承载力特征值计算经验公式和基于t分布的地基承载力优化计算公式进行对比,其置信概率如图4所示。
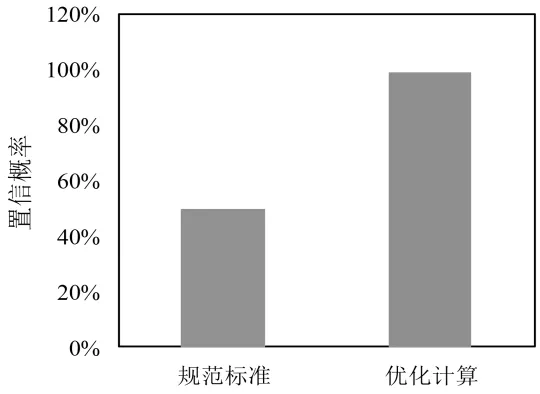
图4 置信概率对比示意图
由图4可知,规范推荐的地基特征值偏大,其置信概率仅有50%;基于t分布的地基承载力特征值稍小,其置信概率可以达到99%。
5 结语
运用统计学的基本原理对中粗砂、粉细砂和黏性土的地基承载力特征值经验公式进行了优化,可以得到以下结论。
(1)规范中的标准贯入锤击数与地基承载力特征值对照表是基于大量试验进行统计得出的,其保证率只有50%。
(2)基于t分布的地基承载力优化计算公式考虑了数据统计的误差,其置信概率可达99%。
(3)修正的地基承载力计算公式综合考虑了统计误差的影响,相对于规范中的经验值,其计算结果略低,置信概率更高。修正的地基承载力优化公式可以为计算地基承载力特征值提供参考。
