Mlinex损失函数下Weibull分布的Bayes估计

范梓淼, 赵江南, 马文杰

(新疆农业大学 数理学院, 新疆 乌鲁木齐市 830052)

0 引言

在Bayes统计决策中,后验风险最小准则下,损失函数决定着后验风险,从而影响决策的优劣. 损失函数大致分为对称和非对称,Mlinex损失函数是Podder在研究Pareto分布参数估计问题时引入的一类非对称损失函数[1],被广泛应用在Bayes估计问题中.在Mlinex损失函数下[2-4],分别讨论了一类分布族参数、Gamma分布的尺度参数、逆伽马分布尺度参数的Bayes估计,并证明Mlinex损失函数的优势.

Weibull分布于1951年由瑞典科学家Waloddi Weibull正式命名,引入到可靠性分析中,用于可靠性工程和各种寿命试验的数据处理,有较好的拟合性和灵活性.例如，郑明亮建立Weibull分布下的加速寿命试验方案[5],许凌天[6]和李刊等人[7]选择Weibull分布建模,分别对轴承和钢筋/混凝土可靠性寿命进行评价研究.因此,研究Weibull分布的各种性质尤其是参数估计问题是有意义的.为节省成本和试验时间,截尾数据被实际应用和研究普遍使用,逐步增加Ⅱ型截尾是一类定数截尾数据. 在逐步增加Ⅱ型截尾下,徐晓岭讨论Weibull分布的极大似然估计和逆矩估计[8];李风等人基于平方损失和Linex损失,讨论Weibull分布的Bayes估计[9].本文将在Mlinex 损失函数进一步研究Weibull分布的Bayes估计问题,并用Monte Carlo模拟,比较各估计的优劣.

定义1 若随机变量X的密度函数为

则称X服从韦布尔分布,记作W(m,η),其中m>0,η>0.韦布尔分布的分布函数为

1 Mlinex损失函数

Mlinex损失函数是一种修正线性指数损失函数,其表达式为

(1)

其中δ是θ的任一估计,c是不为0的常数,不妨设c>0.

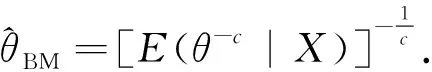
2 逐步增加Ⅱ型截尾模型

设有n个样品进行试验,当第一个失效样品出现时,记试验时间为x(1),同时从剩下的n-1个样品中抽出r1个退出试验;再继续观察剩余的n-1-r1个样品,当第二个失效样品出现时,记时间为x(2),从n-2-r1中抽出r2个退出试验;当失效k个时,记时间为x(k),退出rk个样品.由此得到,失效时间(x(1),x(2),…,x(k))为逐步增加Ⅱ型截尾数据,为方便记为x=(x1,x2,…,xk).当k=n时,为定数截尾数据.

引理2[10]设x=(x1,x2,…,xk)来自逐步增加Ⅱ型截尾样本,则其联合密度函数为

3 Mlinex损失函数下Weibull分布的Bayes估计

定理1 设x=(x1,x2,…，xk)来自逐步增加Ⅱ型截尾模型下Weibull分布W(m,η),其中m已知,η未知,参数空间为Θ={η|η>0}.假设η的先验分布为逆伽玛分布IG(α,λ),则在Mlinex损失函数下,参数η的Bayes估计为

且该估计是容许的.

证明由引理2知,样本的联合密度为

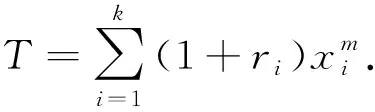
η的先验分布为

则联合密度为

从而,后验密度为

所以,在样本给定后,η的后验分布为IG(α+k,T+λ),即

η|x～IG(α+k,T+λ).

由

于是,在Mlinex损失函数下,参数的贝叶斯估计为

由引理1知, Bayes估计是唯一的,可容许的.

4 数值模拟

用R语言生成m=25,η=2的逐步增加Ⅱ型截尾下Weibull分布随机数[9],取先验分布参数α=2,λ=3,重复1 000次,求得各估计的均值和均方误差根,如表1所示.其中:

表1 参数各估计的均值和均方误差根

分别为参数η的在平方损失下的贝叶斯估计和最大似然估计

数值模拟表明,合理选择先验分布和c的值,Mlinex损失下Weibull分布参数的Bayes估计较平方损失下的Bayes估计和最大似然估计更接近真实值,更稳健.也说明非对称损失比对称损失函数更具灵活性,便于工程实际应用.