基于周期性结构带隙机理的高速铁路轨道减振降噪研究综述

冯青松, 张瀚文, 戴承欣, 杨舟, 郭文杰

（华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室, 江西 南昌 330013）

0 引言

近些年我国高速铁路技术发展迅速, 列车运行速度不断提高, 轮轨间剧烈的相互作用引起一部分较低频率的振动传递给轨下结构, 而中高频率的振动则会沿钢轨纵向传播, 容易引发诸如波磨[1］等钢轨伤损, 给行车安全及轨道使用寿命等带来不利影响, 同时振动产生的噪声也会给乘客和沿线居民带来困扰[2-3］。所以, 研究和解决铁路轨道结构振动及噪声问题已成为我国高速铁路技术领域的工作重点之一。

由于高速铁路轨道结构沿线路纵向具有很强的周期性, 而周期性结构已被证实具有带隙特性[4］, 当振动以弹性波的形式在周期性结构中传播时, 在特定的频率范围内无法通过, 相应的频率范围被称为带隙。因此, 基于带隙机理对铁路轨道结构中弹性波传播进行分析和调控也成为研究高速铁路减振降噪的一种新思路。

1 周期性结构带隙机理及分析方法

1.1 带隙机理

近代相关的物理学研究发现周期性结构有明显的衰减域特性, 即振动带隙特性, 而振动在结构中通常是以弹性波的形式存在, 所以振动带隙也可称为弹性波带隙, 1种周期性结构中可能存在多条带隙, 然而它们的产生机理却不尽相同。在关于弹性波带隙的研究中, 应该清楚每一种带隙的属性和其产生的机理。

目前, 周期性结构弹性波带隙产生的机理分为[5］Bragg散射机理和局域共振机理。

（1）Bragg散射机理[6-7］中带隙是由弹性波在元胞的边界处发生散射产生的, 本质是利用结构本身的周期性影响波的传播, Bragg带隙出现的频率位置较固定, 通常出现在中高频（铁路结构为1 000 Hz以上[8-9］）, 且主要受元胞的结构和材料影响。

（2）局域共振机理于2000年由Liu等[10］提出, 其特点是不受Bragg散射机理条件的限制, 对应的波长远大于晶格尺寸, 局域共振机理中的元胞可简化为质量-弹簧系统, 其带隙所在频率段与系统的共振模式及质量块固有频率关系密切, 铁路轨道结构频率一般在300 Hz以内[11-12］。

1.2 分析方法

周期性结构带隙的常用计算方法可分为两大类：数值计算方法和解析/半解析方法。数值计算方法以有限元法[13-14］为主, 解析/半解析方法包括传递矩阵法[15-16］、平面波展开法[17-18］和能量法[19-20］等。

1.2.1 数值计算方法

有限元法的基本原理是将连续弹性体离散化为一定数量的有限小的单元集合体, 根据弹性力学的基本方程和变分原理分析单元结点力和结点位移之间的关系并建立有限元方程, 再引入边界条件求解线性方程组以及计算单元应力。该方法概念清晰浅显、适用性强、收敛性好, 但目前能够直接用于计算带隙的商业软件较少（主要是瑞典COMSOL公司研发的COMSOL Multiphysics多物理场耦合分析软件）。同时, 有限元法的计算准确性很大程度上依赖网格尺寸大小, 难以兼顾计算精度和计算成本。

1.2.2 解析/半解析方法

（1）传递矩阵法可以非常便捷高效地求解出一维结构的带隙, 如周期性弹簧支撑的钢轨带隙计算。传递矩阵法基于周期性结构中应力、位移等参数的基本方程, 并与边界处的连续条件结合, 得到单个周期的结构传递矩阵；通过矩阵之间相乘得到有限长周期性结构振动传输特性的解析解。但该方法在处理多维结构时并不适用。

（2）平面波展开法作为计算带隙特性最基本的方法之一, 其主要思路是基于周期性结构的材料参数和结构参数均具有周期特性, 把周期性结构中同样具有周期特性的材料、结构等参数按傅里叶级数展开, 同时结合Bloch定理将周期性结构中弹性波的波动方程转化成特征值求解的形式, 从而得到该结构的频散曲线。该方法可用于多维结构的带隙求解, 但由于受限于需要直接求解微分方程组, 在处理复杂的边界条件时较困难。

（3）能量法[21-22］可以将微分方程边值的求解问题转化为泛函极值问题, 易于求解复杂结构的耦合问题, 所以近年来也被用于周期性结构的带隙求解, 但能量法在计算周期性结构带隙时, 一是需要构造形函数以满足周期性边界条件, 这个构造过程难度较大；二是构造后形函数的质量及刚度矩阵都包含了波数, 随波数变化进行循环计算必然会带来计算成本增加。

此外, 也有一些新提出的方法可用于计算周期性结构带隙, 如谱动刚度法[23］、小波法[24］、渐进匹配展开法[25］等, 虽然这些方法各具特点, 但都不适用于处理一些复杂周期性结构。为克服传统周期性结构带隙计算方法的局限性, 文献[26-27］提出一种改进型能量法, 通过引入人工弹簧[28-30］模型来模拟周期性边界条件, 无需再构造满足周期性边界条件的形函数, 将周期性边界上的约束转换为人工弹簧的弹性势能, 因此仅在周期性边界弹性势能矩阵中包含了波数, 而其他矩阵只需计算1次, 极大地提高了周期性结构带隙的计算效率。由于人工弹簧模型使用灵活、便捷, 未来可进一步拓展到更复杂的周期性组合结构带隙分析中, 但目前该方法仅能直接求出弹性波矢k的实部随频率变化的频散曲线, 尚无法得出波矢k的虚部与频率的关系, 即无法反映波在结构内部的衰减情况。

2 周期性铁路轨道振动

2.1 周期性铁路轨道结构振动

目前, 国内外已有一些学者开展了关于周期性铁路轨道振动分析方面的研究, Mead[31］基于行波分析法, 将铁路轨道简化为无限长的周期性梁并首次给出了其结构带隙特性。Heckl[32］考虑轨枕和道砟的影响, 在模型中将轨枕和道砟分别考虑为质量块和弹簧, 研究周期性支承铁木辛柯梁中压缩波、弯曲波、扭转波的振动特性。Grassie等[33］用一种周期性梁结构模拟铁路轨道结构, 并基于广义状态矩阵法计算出导纳函数。Thompson[34］分析周期性支撑钢轨结构的振动衰减率特性, 发现钢轨结构在pinned-pinned频率附近存在衰减区域, 但未对此作进一步分析。文献[35-37］利用2.5维有限元法求出谐荷载作用下周期性铁路轨道结构的动力响应。王平等[9, 11］结合传递矩阵法和布洛克定理分析周期性铁路轨道结构的带隙, 发现Bragg带隙和局部共振带隙在结构中并存, 并且研究了我国高速铁路CRTSⅠ型无砟轨道结构, 求得其频散曲线。易强等[38］基于传递矩阵法与布洛克定理得到了铁路有砟轨道结构的带隙, 采用功率流法研究了弹性波能量在铁路有砟轨道内的传播特性, 并分析了弹性波在周期性三维轨道结构中的耦合与转换规律。

冯青松等[39］基于点支承铁木辛柯梁和平面波展开法得到周期性离散支承钢轨结构的垂向振动带隙, 分析钢轨阻尼、扣件阻尼以及钢轨温度力对带隙特性的影响, 并分析有限周期性铁路轨道结构中振动能量的传递特性, 为无缝线路的温度力检测和轨道结构振动及噪声控制提供了新思路。此外, 冯青松等[40］还以我国高速铁路CRTSⅡ型和CRTSⅢ型板式无砟轨道为研究对象, 分析铁路轨道的分层特性, 将其视为周期性梁-板组合模型, 周期性高速铁路无砟轨道力学模型见图1, 并基于一种改进的能量法, 计算得到上述2类铁路无砟轨道结构在0~1 200 Hz频率的带隙特性, 通过对各带隙的形成机理进行分析, 准确评估了弹性波在铁路轨道结构带隙传播的频率范围及路径（见表1）, 为今后实现结构的精细化减振提供了理论依据。总体来看, 现有的研究多围绕能带结构开展, 鲜有将其和响应特性结合进行分析的, 缺乏工程上的评价指标分析, 此外, 目前还未见关于铁路曲线段轨道结构振动研究的相关报道。

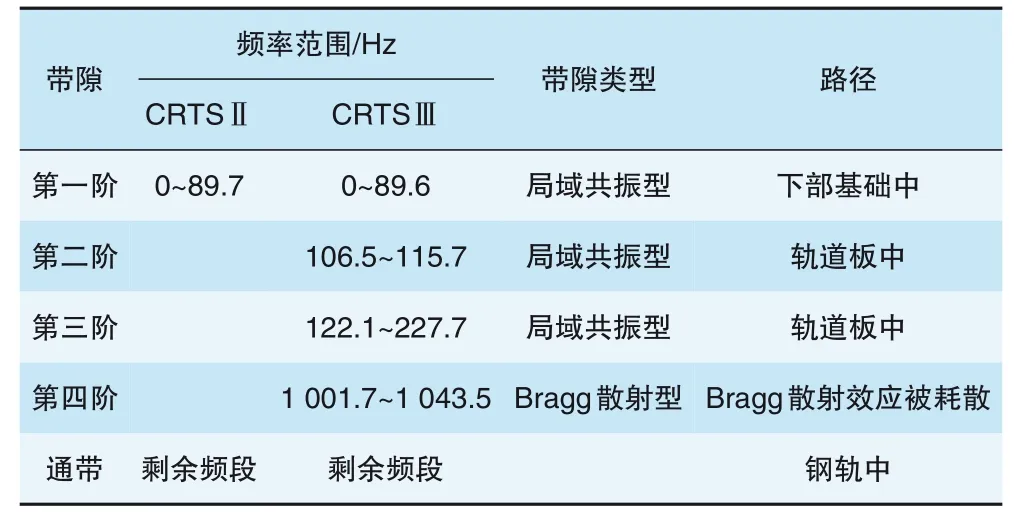
表1 0~1 200 Hz两类高速铁路无砟轨道结构带隙弹性波传播的频率范围及路径

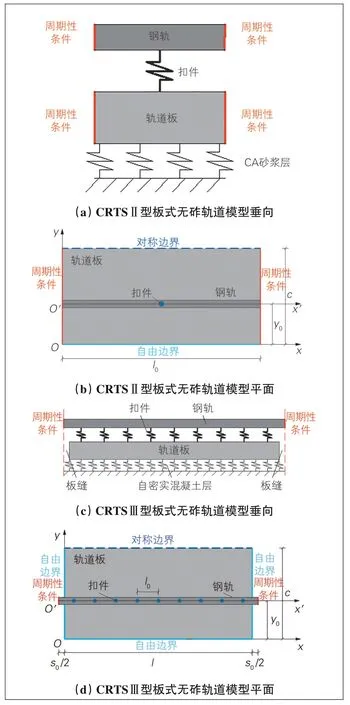
图1 周期性高速铁路无砟轨道力学模型

2.2 周期性桥梁振动

高速铁路大多修建在高架桥梁上, 而铁路桥梁沿线路方向也具备明显的周期特性, 在周期性桥梁的振动理论方面, Metrikine等[41］和Vostrukhov等[42］将高架桥梁铁路轨道作为周期性连续梁结构, 分析列车的不同行驶速度以及黏性参数对高架铁路轨道结构动力响应的影响。文献[43-45］基于传递矩阵法、傅里叶变换法、有限元法等提出刚性支撑的周期性简支高架桥梁的计算模型, 周期性高架桥梁示意见图2, 并基于此得到了周期性桥梁自由振动的特征方程以及考虑移动荷载和移动质量作用下响应的计算结果, 研究系列移动荷载下周期性铁路高架桥梁的共振和消振效应[46-48］, 以及桩基础支撑缺陷周期桥的动力响应与缺陷态之间的关系, 发现产生共振的响应局域在缺陷跨度附近[49］。范胜帅等[50］考虑了移动车辆对周期性铁路高架桥梁的作用, 将车桥作用力展开为Fourier级数, 计算得到周期性高架桥及车辆的动力响应。曹艳梅等[51］基于无限周期结构理论建立桥梁有限元模型, 提出在任意荷载列作用下得到桥梁结构周期性单元等效结点荷载矢量频谱的计算方法, 并以32 m等跨径布置铁路高架桥梁为例分析其能带特性、动力响应以及墩底动反力。Chen等[52］利用Fourier变换方法和有限元方法分析移动质量和地震波同时作用下无限周期高架桥梁的动力响应, 结果表明移动质量和地震波同时作用下平面内横向位移比由地震波单独引起的横向位移大, 而其面外振动的横向位移则通常比地震波单独引起的横向位移小。目前所有关于周期性铁路高架桥梁振动响应的研究仍未全面考虑桥-轨耦合效应以及桥梁曲线段的特殊性, 研究移动车辆作用下桥梁振动的动力响应也未将桥上轨道短波不平顺特性纳入考虑范围。

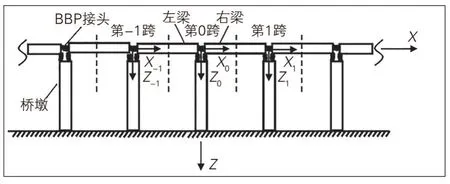
图2 周期性高架桥梁示意图

3 周期性铁路轨道振动噪声控制

3.1 轨道振动控制

目前针对铁路轨道的减振、隔振措施有很多, 包括阻尼钢轨、钢轨动力吸振器以及隔振垫等。其中钢轨动力吸振器本质上基于周期结构带隙理论中的局域共振机理, 其作用原理是在钢轨上施加质量-弹簧-阻尼系统, 通过调节动力吸振器结构参数使固有频率与钢轨结构的频率匹配, 从而同钢轨产生谐振以此来减少钢轨振动。Thompson等[53］设计一种用于钢轨的调谐质量阻尼器（TMD）, 通过在实验室和现场进行降噪性能测试, 发现该钢轨TMD结构对钢轨辐射噪声具有明显的衰减作用。王刚[54］建立布置动力吸振器的欧拉梁模型, 并使用传递矩阵法推导出结构中弯曲波和纵波带隙的计算表达式。郁殿龙[55］在文献[54］的基础上, 将欧拉梁替换成铁木辛柯梁, 并附加一种双自由度振子, 利用传递矩阵法计算出该结构的带隙。Xiao等[56］研究周期规律, 并发现当引入的局域谐振带隙接近布拉格带隙时可以形成伪超宽带隙。这些研究也被扩展到了铁路领域。孟铎[57］对周期性附加吸振器的铁路轨道结构带隙特性进行研究, 分析了吸振器参数对带隙的调控规律。Wang等[58］同样基于局域共振机理研究周期性布置吸振器的铁路轨道结构的带隙特性, 附加吸振器的周期性铁路轨道结构见图3, 发现结构中新引入的局部谐振带隙与原铁路轨道结构带隙之间存在耦合和跃迁现象, 在耦合的位置带隙宽度达到最大, 从而实现对铁路轨道结构中弹性波传播的抑制。

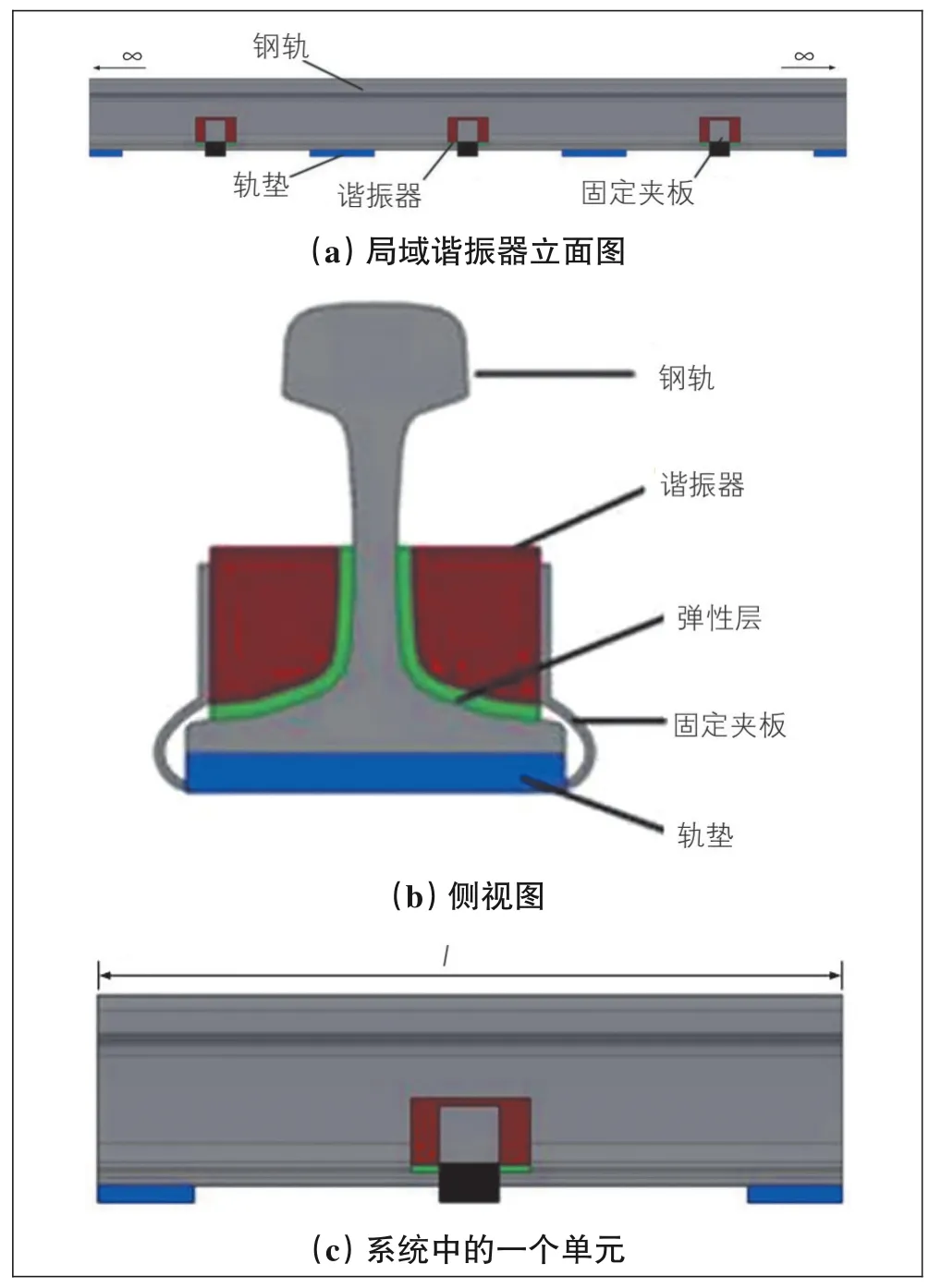
图3 附加吸振器的周期性铁路轨道结构

周期性结构的带隙控制机理同样也被应用于隔振措施的研究中。李粮余[59］利用有限元软件将基于周期性结构局域共振机理设计的新型隔振垫和普通隔振垫的隔振效果进行对比分析, 结果表明新型隔振垫具有良好的隔振效果, 尤其是频率为63~100 Hz时效果更明显, 同时新型隔振垫还具有动力吸振的作用, 可以将振动能量耗散掉。徐涆文等[60］基于周期性结构原理建立能够不受边界反射波干扰的有限元轨道模型并分析弹性短轨枕结构（见图4）的隔振性能, 发现弹性短轨枕结构轨道同普通板式结构轨道相比具有更好的隔振效果。在研究的频率范围内隔振率都稳定在1。Hu等[61］设计出一种新型周期性分层轨道结构, 基于带隙控制机理优化几何及材料参数来调整结构的带隙频率范围, 从而实现铁路轨道结构振动衰减。徐司慧等[62-63］分析应用于铁路轨道的黏弹性层状周期性板的隔振性能, 提出在单位移动谐荷载作用下, 对边自由对边简支板动力计算的近似理论及解答, 并分析几点影响黏弹性层状周期性板减振效果的因素, 以便对其进行减振设计。为进一步利用带隙机理抑制铁路轨道振动噪声提供了新思路。

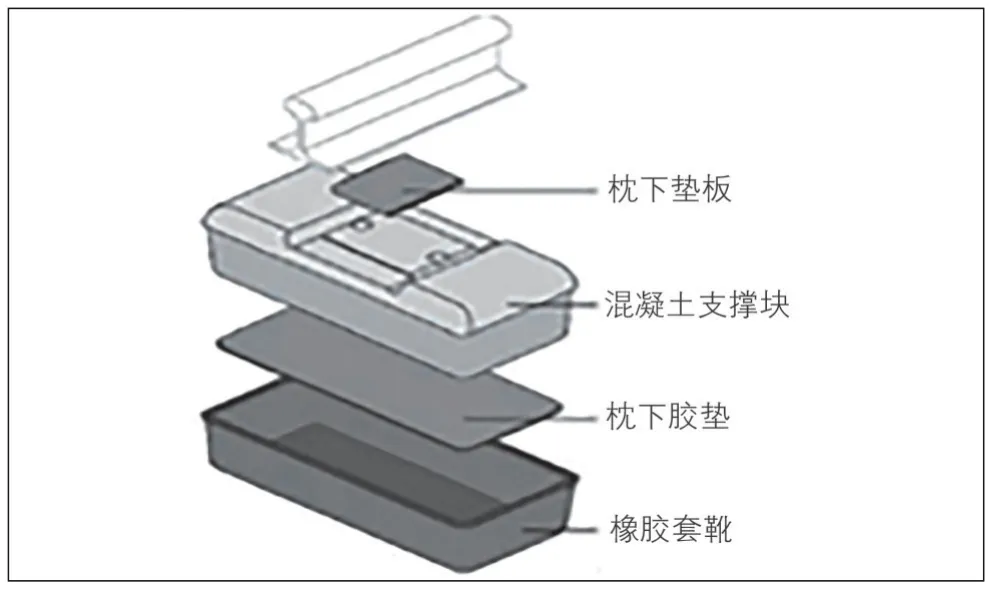
图4 弹性短轨枕结构

3.2 声屏障噪声控制

设置声屏障作为一种在传播途径中控制噪声的行之有效的方法, 被广泛应用于轨道交通降噪领域。近年来一些学者也开始基于带隙特性设计性能更优异的周期型声屏障。Koussa等[64］在传统的声屏障结构内侧布置了声子晶体结构, 发现布置声子晶体的改进型声屏障在中高频段内能更好地阻隔交通噪声的传播。Morandi等[65］建立了由3层周期性排列的PVC管组成的声屏障足尺模型, 研究对声辐射的反射及透射特性, 发现其在布拉格带隙频率附近获得了最大插入损失。Elford等[66］将散射体换成竹、木、金属等材料, 并附加上空腔结构和吸声材料, 形成一种包含亥姆霍兹共振机理的新型周期型声屏障, 并在试验环境下取得了良好的声衰减效果。李硕[67］提出一种嵌入了周期性局域共振结构的均匀板结构, 在局域共振带隙频段内实现了隔声性能的提升。张佳龙等[68］提出了一种正八边形孔状局域共振型声子晶体结构, 发现其在中低频范围具有良好的隔声特性。易强等[69］基于带隙理论设计了一种气-固周期型声屏障, 基于传递矩阵法对其声波带隙特性进行了研究, 结果表明增加气固周期型声屏障中的固体材料密度可明显使带隙的起始频率降低, 同时可以提高带隙的截止频率, 拓宽带隙的宽度, 气固周期型声屏障可以在实现声屏障轻质化的同时达到较好的降噪效果。

上述研究表明相较于传统声屏障, 周期型声屏障在控制噪声频率范围方面具有更多主动性及针对性, 为轨道交通噪声控制提供了全新的研究思路和方法。我国目前还没有将周期型声屏障运用到实际工程中, 因而有巨大的潜在研究及应用价值。

4 结论

对周期性结构带隙机理和研究方法、周期性铁路轨道中弹性波传播特性以及基于该理论的轨道结构振动与噪声控制等方面的研究进展进行了回顾。目前, 关于周期性结构带隙机理的研究已经有了很多理论成果, 利用带隙机理调节周期性铁路轨道和减隔振构造物的参数可以对振动噪声进行特定频率范围的针对性控制, 从而达到适用于各种应用场景的减振降噪效果。因此, 周期性结构带隙机理在铁路轨道减振降噪方面拥有广阔的应用前景, 就当前的发展现状而言, 后续研究工作可主要围绕以下几点开展：

（1）现有的针对高速铁路轨道结构带隙机理研究中, 轨道结构力学模型相对简化, 大多考虑为单层梁、梁-质量块或梁-梁模型, 这些都忽略了轨道板和底座板的动力学行为。事实上, 高速铁路无砟轨道结构为层状组合结构, 其中的轨道板和底座板除了会发生刚体运动, 还会进行弹性体运动, 显然会对弹性波在轨道结构中的传播产生影响, 从而不利于铁路轨道结构振动与噪声的精准控制。

（2）已有关于周期性铁路轨道带隙机理的理论研究基本都是针对直线线路的轨道结构, 而鲜有针对曲线线路的周期性轨道结构弹性波传播特性开展深入研究。在实际工程中, 曲线线路占有很大比例, 研究其内部的弹性波传播行为具有较强的现实意义。

（3）目前的周期性铁路轨道带隙理论研究中, 主要考虑单一轨道结构的带隙特性, 而忽略轨下基础的影响, 尤其是桥梁和隧道这类结构。实际上, 多数高速铁路线路中, 桥梁和隧道是铁路轨道的主要承载基础, 需要进一步分析弹性波在轨道-桥梁或轨道-隧道耦合系统中的传播特性。

（4）目前基于带隙理论的铁路轨道减振降噪研究中, 带隙宽度和位置调控常受周期单元尺寸大小（如扣件间距和轨道板长度）、质量及刚度等因素的限制。然而, 考虑轨道服役期间的功能性和安全性, 周期元胞的基本物理参数不能随意改变, 可以尝试给基体结构附加多个不同的谐振单元或引入其他的物理场（例如引进惯容器、准零刚度机构、压电元件等）以改变结构原本的带隙特性, 实现弹性波的灵活调控, 并据此进一步设计满足实际工程需要的轨道减隔振产品。

（5）目前关于高速铁路噪声控制方式相对单一, 且为被动式降噪, 如在线路两侧设置声屏障。事实是, 声音一旦离开噪声源, 其传播路径十分复杂, 导致传统的声屏障降噪效果不佳。因此, 后续研究应注重主动式降噪机构的研发, 如将轨道板设计为声学黑洞结构, 从而实现振源处降噪。

（6）基于周期性结构带隙机理开展弹性波或声波控制研究, 适用于周期特性明显的结构, 如周期性离散支撑的钢轨和周期性排列的声屏障。然而。对于周期性不明显或者参数变化后不再具有周期特性的结构, 如钢轨的道岔, 目前尚未对该理论开展适用性研究。

（7）现阶段的理论研究普遍和实际工程中的需求脱节, 因根据实际工程中对不同频段减振降噪的需求灵活调控和抑制弹性波, 才能达到预期的减振降噪效果。