高速铁路高架桥梁无缝道岔群结构检算与优化设计
2022-09-22蔡小培王铁霖杨憬帆徐凌雁
蔡小培, 王铁霖, 杨憬帆, 徐凌雁
(1.北京交通大学 土木建筑工程学院, 北京 100044;2.中国铁路设计集团有限公司 线路站场枢纽设计研究院, 天津 300308)
0 引言
我国幅员辽阔, 地形地貌和地质构造复杂, 而随着高速铁路对结构空间的限制要求以及对高速铁路运营、平顺性要求越来越高, 布设在高架桥梁上的车站和道岔也越来越多。桥上无缝道岔轨道结构力学行为复杂且受多重荷载作用[1], 综合了无缝线路、无缝道岔、无砟轨道等技术要点。桥上无缝道岔与下部基础结合衍生出一系列的技术难点, 如跨区间无缝线路与长大桥梁的适应性问题、桥上无缝道岔结构变形的控制问题等[2], 是轨道工程研究领域面临的技术难题之一。
诸多学者对桥上无缝道岔力学特性开展了大量研究工作。王平等[3]建立了长大连续梁桥上无缝道岔的计算模型, 以60 kg/m钢轨12号可动心轨道岔为例, 分析了在长大连续梁桥上铺设无缝道岔及伸缩调节器时, 墩台及钢轨的受力变形规律;曾志平等[4]将道岔、桥梁和墩台视为整体, 建立了桥上无缝道岔有限元模型, 根据变分原理和“对号入座”法则建立有限元方程组, 研究了支座布置形式、轨温及梁温变化幅度、扣件及道床阻力、限位器数量、梁跨长度和桥墩刚度等对无缝道岔力学特性的影响。蔡小培等[5]以高速铁路64 m主跨连续梁桥上无缝道岔为研究对象, 建立了无缝道岔-无砟轨道-桥梁空间耦合模型, 分析了温度作用、列车荷载以及断轨时大跨桥上无缝道岔的力学特性, 提出了一套适用于大跨桥梁无缝道岔的检算方法和轨道结构优化方案。高增增[6]以高架站咽喉区桥上单渡线和单开道岔为研究对象, 建立了线桥墩一体化模型, 研究了在铺设常阻力方案、不同小阻力方案和道岔梁间插入简支梁方案时, 无缝线路和无缝道岔轨道受力和变形规律。
桥梁温度跨度较大时, 在温度作用下无缝道岔纵向力较大, 道岔-桥梁相互作用明显[7]。道岔区钢轨温度力通过尖轨跟端和辙叉区的间隔铁传递, 使无缝道岔受力变形更加复杂;无缝道岔群布置在高架桥上时, 在列车荷载作用下桥梁会产生挠曲变形, 导致无缝道岔受力变形增大, 加剧轨道不平顺。为满足无缝道岔强度、稳定性等要求, 保证线路安全运营, 需要对轨道结构进行优化设计。文献[8-9]推荐使用小阻力扣件以减小钢轨受力, 但针对桥上无缝道岔群小阻力扣件的布设原则和具体布设方案尚缺乏系统性研究。
以某高速铁路高架桥上由8组无缝道岔构成的道岔群为例, 介绍高架桥上铺设无砟轨道无缝道岔群的精细化建模方法, 系统分析温度、挠曲及制动作用下桥上无缝道岔群及桥墩墩顶的受力和变形特性, 提出桥上无缝道岔设计方法, 探讨铺设小阻力扣件优化设计方案的可行性。
1 结构参数与荷载作用
1.1 桥上无缝道岔结构参数
无缝道岔与桥梁结构的相对位置、桥跨的布置形式、道岔号码等直接影响道岔区钢轨的受力变形特性。对于道岔群结构, 由于道岔间存在顺接、对接等连接方式, 无缝道岔受力变形更加复杂。算例中的高架桥上均铺设客运专线18号可动心轨单开道岔, 直线通过速度350 km/h, 道岔位置、桥梁墩台编号及桥跨范围见图1。
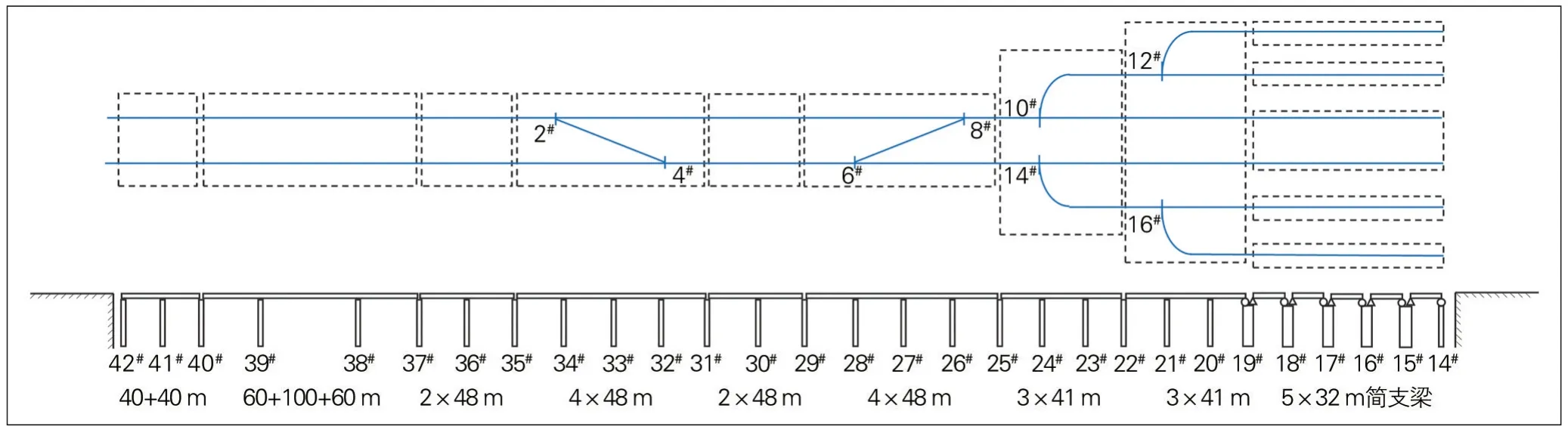
图1 桥上无缝道岔示意图
(1)桥梁。桥梁型式依次为:(40+40)m T型刚构、(60+100+60)m连续刚构、2×48 m连续刚构、4×48 m连续刚构、2×48 m连续刚构、4×48 m连续刚构、3×41 m双线变四线道岔梁、3×41 m双线变三线道岔梁、5×32 m简支箱梁。
(2)轨道。桥上道岔为客运专线18号可动心轨单开道岔, 采用U75VG材质60 kg/m钢轨, 屈服强度为472 MPa, 考虑1.3的安全系数, 容许应力为363 MPa。
1.2 设计荷载
列车荷载采用ZK活载, 轮轨摩阻系数取0.164。最高轨温为49.6℃, 最低轨温为-39.5℃, 设计锁定轨温为(10±3)℃, 钢轨最大温降为52.5℃, 最大温升为42.6℃;根据TB 10015—2012《铁路无缝线路设计规范》(简称《规范》), 混凝土梁考虑年温差, 温差变化30℃。按ZK活载施加挠曲和制(启)动作用, 按结构最大升降温施加温度作用, 并分析极端气温下钢轨折断对桥墩墩顶纵向力的影响。
2 空间耦合模型建立
根据客运专线18号可动心轨单开道岔设计参数、岔区无砟轨道与桥梁的实际布置情况, 基于道岔-桥梁相互作用原理、非线性有限元理论, 考虑道岔、无砟轨道、桥梁及墩台的相互作用, 建立无缝道岔-桥梁-墩台空间耦合模型(见图2)。为消除边界条件的影响, 桥梁两侧各建立150 m路基段。
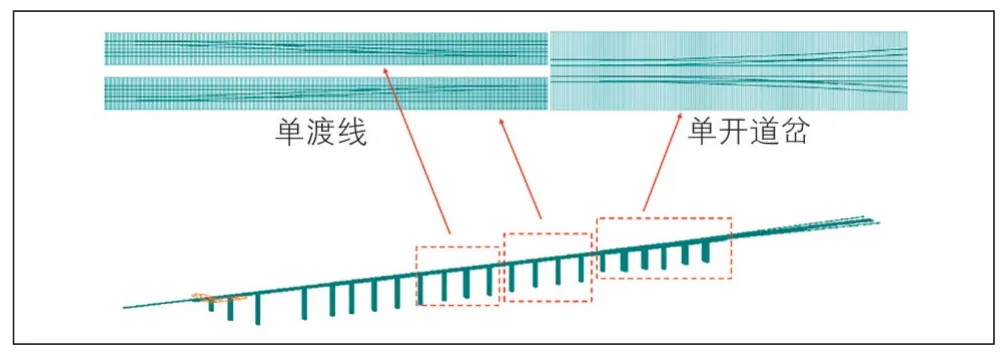
图2 无缝道岔-梁体-墩台空间耦合模型
高架桥的梁体、桥墩采用梁单元模拟, 梁体-墩顶共用节点, 墩台底部地基采用节点弹性支承模拟。
钢轨采用梁单元进行模拟, 考虑纵向、横向及垂向位移。道岔尖轨与可动心轨前端可自由伸缩, 尖轨或可动心轨尖端位移为其跟端位移与自由段伸缩位移之和。间隔铁阻力使用非线性弹簧单元模拟, 阻力值采用相关试验取得的数据[10]。
扣件纵向阻力采用非线性弹簧单元模拟, 横向阻力采用线性弹簧单元模拟, 作用于钢轨支承节点上, 限制钢轨相对于桥梁的纵、横向位移, 纵、横向阻力根据《规范》取值。扣件纵向阻力取值见表1。
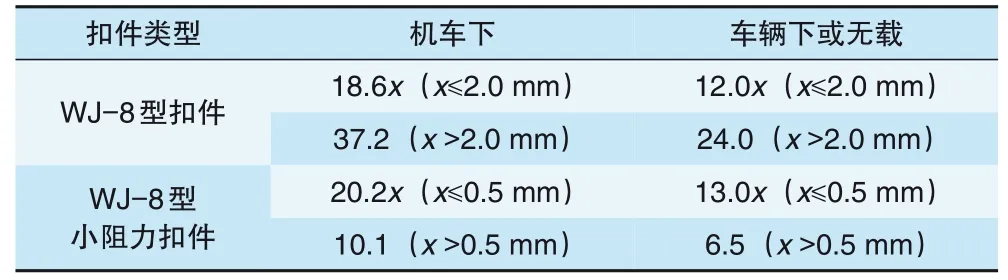
表1 扣件纵向阻力 kN/(m·轨)
3 力学特性与结构检算
桥梁上铺设无缝道岔时, 伸缩力、挠曲力、制(启)动力和断轨力的变化规律与铺设普通无缝线路时均有较大区别[11], 需要重点关注。在桥上无缝道岔检算中, 应根据梁轨相互作用原理, 考虑道岔尖轨与基本轨、道岔与桥梁之间的相互作用。检算内容主要包括桥上无缝道岔钢轨强度、稳定性, 以及桥上无缝道岔部件强度、尖轨位移、心轨位移、道岔转辙器、辙叉与桥梁的相对位移等指标。铺设无缝道岔的桥梁, 墩台结构的设计检算应考虑无缝线路的纵向力。
基于建立的无缝道岔-梁体-墩台空间耦合模型, 分析伸缩力、挠曲力及制(启)动力作用下钢轨受力与变形规律, 并对钢轨强度、桥墩墩顶纵向力等进行检算。
3.1 温度作用
对于温度跨度较大的高架桥, 在升温或降温作用下, 梁缝处钢轨纵向力较大, 无缝线路强度经常不满足《规范》要求。设计中可考虑在简支梁跨、连续梁或刚构桥边跨区域布置小阻力扣件, 在保证道岔正常转换的同时, 减小梁体变形对钢轨纵向力的影响。
考虑全桥铺设常阻力扣件及部分区域铺设小阻力扣件, 将钢轨按最大温降52.5℃进行降温, 根据《规范》, 无砟轨道梁降温30℃, 两工况下钢轨伸缩力见图3。
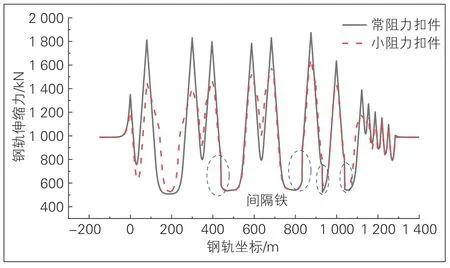
图3 钢轨伸缩力
由于尖轨将温度力通过间隔铁传递给基本轨, 钢轨纵向力在道岔间隔铁所在位置出现突变。铺设小阻力扣件可以减小梁轨相互作用, 在降温幅度相同时, 铺设小阻力扣件时的钢轨伸缩力小于铺设常阻力扣件时的钢轨伸缩力。由图3可知, 降温作用下, 布置常阻力、小阻力扣件时钢轨伸缩力峰值均出现在25#墩所在梁缝处, 大小分别为1 874.21、1 651.65 kN, 即241.99、213.25 MPa。
3.2 列车荷载作用
列车荷载作用主要考虑为垂向的挠曲荷载与纵向的制(启)动荷载。根据《规范》, 伸缩力与挠曲力不叠加。采用影响线加载法确定无缝道岔区域钢轨挠曲力、制(启)动力产生峰值时荷载作用的位置。
3.2.1 挠曲力
考虑列车挠曲荷载位于25#墩起向大号码墩方向400 m的单线直向过岔轨道上, 全桥常阻力扣件和设置小阻力扣件对钢轨挠曲力的影响对比见图4。
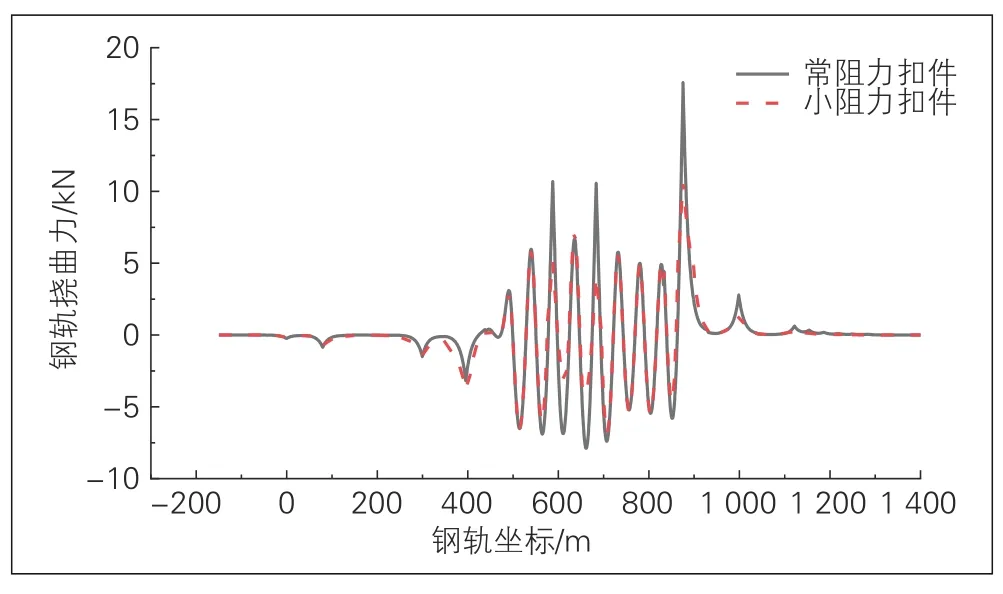
图4 钢轨挠曲力
由于混凝土箱梁截面惯性矩较大, 桥梁截面抗弯刚度大, 对于高架桥上无缝道岔来说, 在挠曲荷载作用下, 无缝道岔区钢轨受力及变形通常较小, 钢轨挠曲力极值出现在连续刚构梁桥墩及梁缝处。由图4可知, 在列车垂向荷载作用下, 挠曲力极值均出现在桥墩处, 布置常阻力、小阻力扣件时挠曲力峰值分别为17.58、10.76 kN。
3.2.2 制(启)动力
为使25#墩梁缝处的无缝线路出现最大制(启)动力, 制(启)动荷载布设在25#墩起向大号码墩方向400 m的单线直向过岔轨道上(见图5)。全桥常阻力扣件和设置小阻力扣件对钢轨制(启)动力的影响对比见图6。
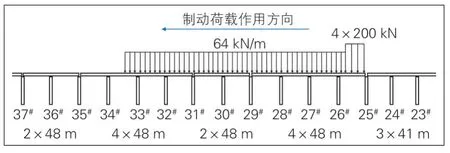
图5 制动力加载示意图
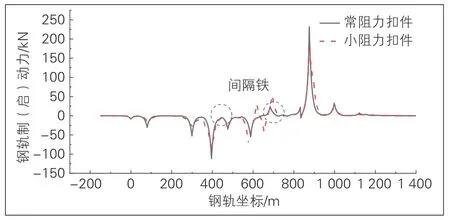
图6 钢轨制(启)动力
与挠曲荷载相比, 制(启)动荷载对桥上道岔钢轨受力及变形影响较为显著, 但远小于温度荷载作用的影响。在制(启)动荷载作用下, 钢轨发生纵向变形, 桥梁与钢轨产生同方向位移, 且与钢轨制动位移较为接近, 钢轨未发生爬行, 道岔几何形位能够得到保证[12]。由图6可知, 钢轨制(启)动力峰值出现在制(启)动荷载作用端部。布置常阻力、小阻力扣件时制(启)动拉力峰值分别为231.80、184.69 kN, 对应应力为29.93、23.85 MPa。制(启)动压力峰值分别为111.78、83.95 kN, 对应应力为14.43、10.84 MPa。梁轨相对位移峰值出现在制(启)动荷载作用端部所在梁缝处(见图7)。铺设小阻力扣件后, 梁轨相对位移有所增加。常阻力、小阻力方案下梁轨相对位移峰值分别为1.62、2.35 mm。
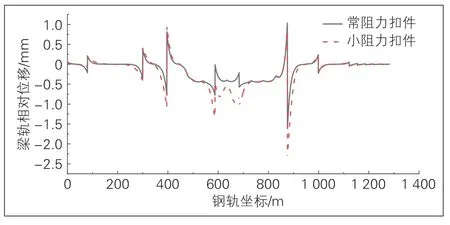
图7 梁轨相对位移
3.3 桥墩墩顶纵向力
3.3.1 温度作用
钢轨最大温降52.5℃, 最大温升42.6℃。根据《规范》, 无砟轨道梁年温差取30℃。计算得到的桥墩墩顶纵向力见图8。
由于桥梁跨度不同, 以及部分桥梁铺设无缝道岔后受道岔尖轨伸缩的影响, 各桥梁墩台所受纵向力相差较大。当桥墩位于连续刚构桥的中部时, 桥墩所受纵向力通常较小;当桥墩位于连续刚构桥的梁端时, 桥梁墩顶纵向力较大。对于双线变四线、双线变三线道岔梁, 桥梁墩顶纵向力受无缝道岔影响较大, 19#、22#、25#边墩墩顶纵向力较大。由图8可知, 钢轨降温52.5℃、无砟轨道梁降温30℃时, 桥墩墩顶纵向力峰值出现在25#墩处, 大小为4 162.39 kN;钢轨升温42.6℃、无砟轨道梁升温30℃时, 桥墩墩顶纵向力峰值出现在25#墩处, 大小为4 030.59 kN。
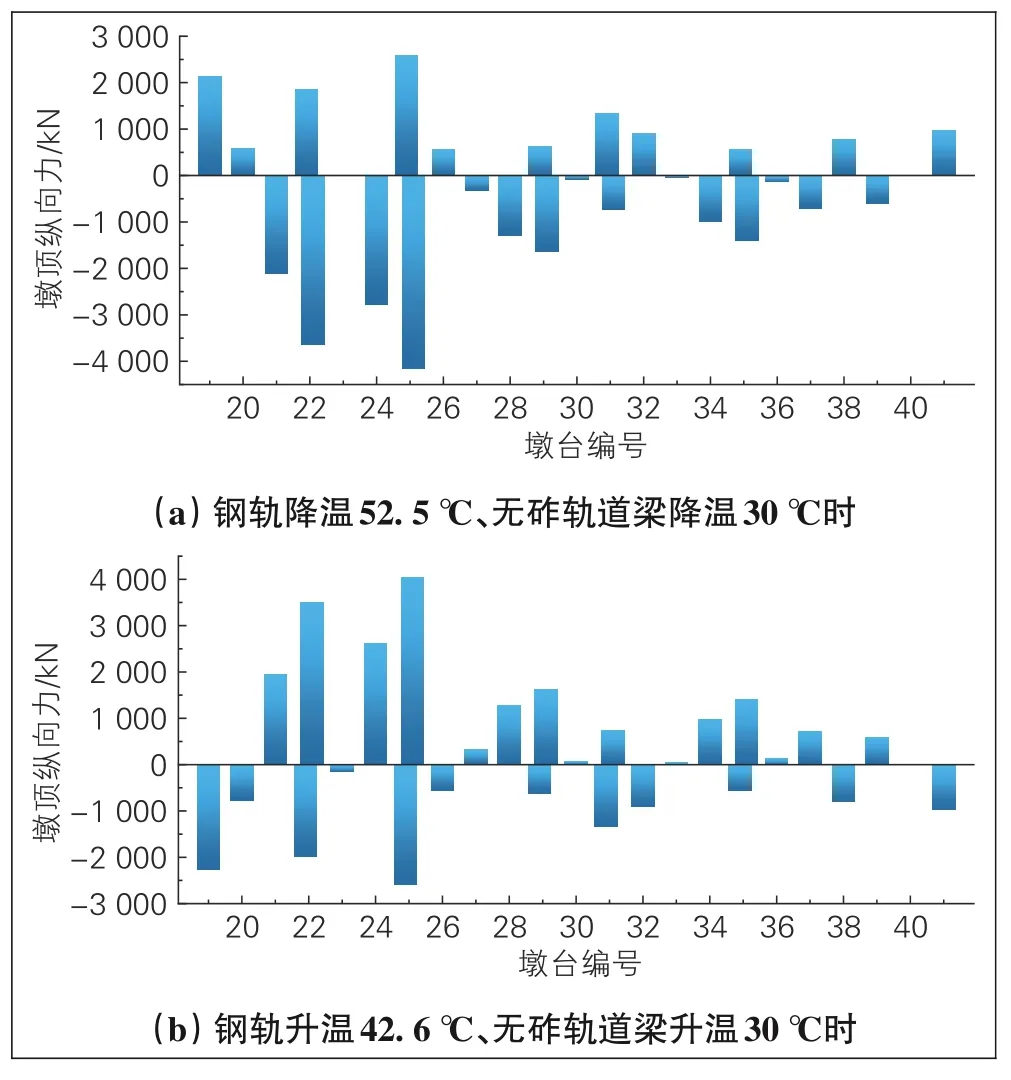
图8 温度作用下桥墩墩顶纵向力
3.3.2 断轨作用
根据钢轨伸缩力峰值出现位置, 考虑在25#墩、29#墩梁缝处单根钢轨折断时, 桥墩墩顶纵向力见图9。
钢轨折断后, 无缝线路的纵向力将重新分布。折断钢轨中的纵向力将得到放散, 未折断钢轨中的纵向力将突然增大, 同时, 桥墩墩顶纵向力将产生突变。钢轨折断时, 折断位置两侧的桥墩中将产生方向相反的力。钢轨折断位置附近的两联桥梁的桥墩纵向力变化最大。如图9所示, 当25#墩梁缝处单根钢轨折断时, 桥墩墩顶纵向力峰值出现在25#墩的4×48 m连续刚构桥一侧, 峰值大小为205.01 kN。当29#墩梁缝处单根钢轨折断时, 桥墩墩顶纵向力峰值同样出现在25#墩, 峰值大小为138.47 kN。

图9 断轨作用下桥墩墩顶纵向力
3.4 钢轨强度检算
全桥铺设常阻力扣件时, 参考《规范》计算得到钢轨动弯拉应力为117.67 MPa。25#墩梁缝位置的伸缩应力最大, 为241.99 MPa, 制动应力为29.93 MPa。将钢轨伸缩应力、动弯应力、制动应力进行叠加, 钢轨所受总应力为389.59 MPa, 超过容许值363.00 MPa(见表2)。因此桥上无缝道岔采用全桥铺设常阻力扣件方案时, 难以满足钢轨强度检算要求, 需要对桥上无缝道岔进行优化设计。

表2 钢轨强度检算 MPa
4 结构优化设计
对于高速铁路高架桥上无缝道岔, 根据结构静力学特性分析可知, 温度荷载对钢轨及桥梁的影响远大于列车荷载作用, 检算时可忽略列车荷载作用的影响。全桥铺设常阻力扣件时, 钢轨伸缩应力较大, 钢轨强度无法满足《规范》要求, 由于设计锁定轨温为(10±3)℃, 温度较低, 难以通过降低轨温减小钢轨伸缩力, 故需考虑布置小阻力扣件。小阻力扣件可有效减小梁轨之间的相互作用, 减小梁体变形对钢轨纵向受力的影响。由于钢轨降温幅度过大, 钢轨纵向力峰值极大, 因此考虑部分区域铺设小阻力扣件(见图10)。18#墩和19#墩之间的简支梁铺设小阻力扣件。对于道岔区域, 道岔前后10 m外布置小阻力扣件, 同时, 小阻力扣件布置范围距离梁缝不超过30 m。对于(60+100+60)m刚构桥, 由于梁端伸缩力较大, 故2个边跨60 m范围布设小阻力扣件, 中间跨100 m范围布置常阻力扣件。
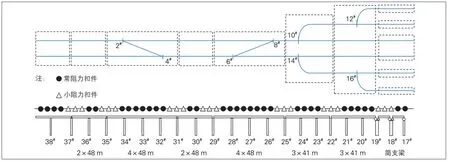
图10 结构优化方案
基于所建立的无缝道岔-桥梁-墩台空间耦合模型, 对优化后的桥上无缝道岔进行受力分析。铺设小阻力扣件时钢轨受力得到改善, 最大应力值较铺设常阻力扣件时明显降低。按小阻力扣件方案设计时, 无缝线路区域钢轨总应力为354.77 MPa, 无缝道岔区域钢轨总应力为304.96 MPa, 与常阻力扣件方案相比, 分别降低8.94%、21.72%, 此时钢轨强度满足《规范》要求。因此, 对小阻力扣件方案其他指标进行检算。
4.1 尖轨、心轨位移检算
尖轨与基本轨、心轨与翼轨的相对位移量对道岔转辙机的牵引转换有重要影响。根据计算, 在温度作用下, 尖轨与心轨的位移量较大, 而在制(启)动荷载作用下较小。温度作用下, 尖轨尖端相对基本轨位移最大在8#道岔, 位移量为15.19 mm, 心轨尖端相对于翼轨位移最大在10#道岔, 位移量为9.60 mm, 对应道岔的尖轨尖端相对基本轨位移均大于心轨相对翼轨位移(见图11)。在温度作用下, 尖轨与基本轨、心轨与翼轨的相对位移均小于《规范》规定的相应限值(40、20 mm)。
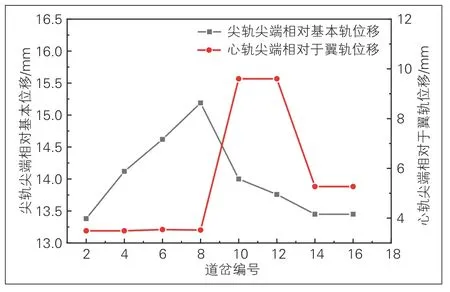
图11 尖轨、心轨相对位移
4.2 转辙器处梁轨相对位移检算
为保证道岔转辙设备的正常运转, 需严格限制转辙器处基本轨与桥梁的相对位移。在道岔施工锁定时, 通常仅关注轨温是否处于锁定轨温, 往往忽略了梁体温度。当道岔在梁体温度较高时锁定, 冬季极端气温下, 梁体降温幅度较大, 转辙器处梁轨相对位移增加(见图12)。当梁体降温幅度达40℃以上时, 转辙器处梁轨相对位移超过限值10 mm。因此, 在无缝道岔铺设时, 应严格控制梁体的温度。

图12 转辙器处梁轨相对位移
4.3 其他指标检算
小阻力扣件方案的各项静力检算结果见表3, 无缝线路强度、钢轨断缝值、间隔铁螺栓强度、梁轨相对位移等指标均可满足《规范》要求。简支梁、道岔以外的梁端区域适当铺设小阻力扣件的方案, 可有效减弱荷载作用下梁轨之间的相互作用, 减小桥梁变形对无缝道岔的受力与变形的影响, 增强结构服役性能并延长使用寿命。
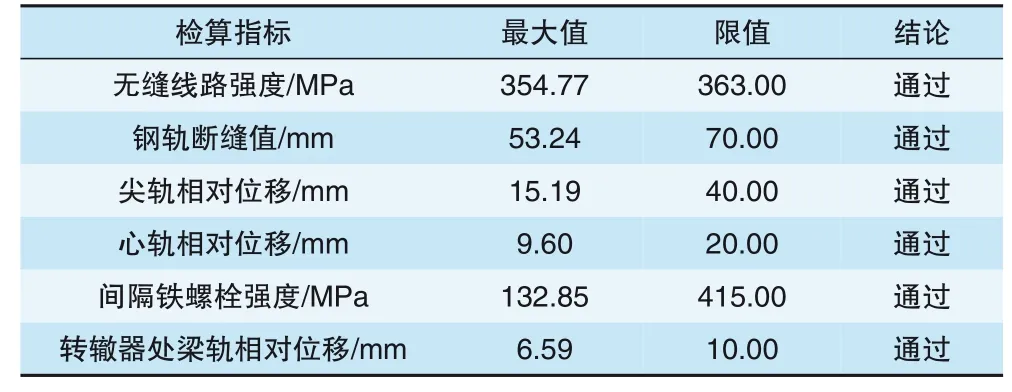
表3 桥上无缝道岔静力检算结果
5 结论
以具体工程实例为背景, 建立了无缝道岔-梁体-墩台空间耦合模型, 对桥上无缝道岔及桥墩墩顶的受力与变形特性进行分析研究, 具体结论如下:
(1)当无缝道岔群铺设于温度跨度较大的多联桥梁时, 无缝道岔钢轨纵向力较大。示例中, 梁端钢轨纵向应力峰值达389.59 MPa, 钢轨强度不满足《规范》要求。在梁端区域铺设小阻力扣件可显著降低钢轨伸缩力峰值。
(2)混凝土箱梁整体性好, 截面惯性矩较大。在列车垂向荷载作用下, 无缝道岔区钢轨挠曲力较小。小阻力扣件方案下挠曲力峰值仅为10.76 kN, 挠曲力不作为钢轨强度检算的控制指标。
(3)当无缝道岔群铺设于跨度较大的连续刚构桥时, 温度作用下桥墩墩顶纵向力远大于断轨时的墩顶纵向力。
(4)无缝道岔铺设时, 建议控制梁体的整体温度接近年平均梁温, 避免夏季高温、冬季低温时转辙器处梁轨相对位移超限, 影响道岔牵引转换。
