液化与非液化场地中直斜双桩动力特性研究

李雨润，辛晓梅，闫志晓，徐栋梁，赵英涛

（1.河北工业大学土木与交通学院，天津 300401；2.河北省土木工程技术研究中心，天津 300401；3.邢台路桥建设集团有限公司，河北邢台 054001）

引言

桩基础相较于其他的基础形式适合于多种复杂的地质情况，应我国的基础设施建设需求桩基在我国应用极为广泛，但历次震害调查表明，桩基础有很大程度的破坏，在液化地基中的桩基础破坏更是尤其严重。例如1976 年唐山大地震中130 座梁式桥被调查，发现桩基破坏严重［1］，天津塘沽新河外运码头的13 对横向叉桩全部破坏［2］；2010年智利大地震中多处桥梁桩基破坏严重［3］。

近年来，国内外学者使用理论分析、模型试验和数值仿真等多种方法开展了桩基础的性能研究。凌贤长、唐亮、苏蕾等［4-6］进行了一系列振动台试验并开展了OpenSees两相完全耦合的u-p形式模拟，总结并评述了液化侧扩流场地桩-土-桥梁结构地震相互作用的基本规律；许成顺等［7-8］基于振动台试验，采用API规范推荐的p-y曲线模型，建立了土-桩-结构系统动力相互作用简化分析模型，探究了地震荷载作用下的砂土液化效应、群桩效应以及承台与土之间的动力相互作用；王睿等、张建民等［9-10］基于Flac3D 开发砂土液化大变形本构模型，并模拟了饱和砂土及等效非线性增量碎石桩模型；周燕国等［11］基于震后调查获得的原位测试指标（如剪切波速）与震前原状土的相应指标之间存在的差异展开研究，评价了砂土抗液化强度评价方法并提出合理修正方法；梁发云等［12］进行了结构-群桩基础的大型振动台地震响应模型试验研究，重点研究了群桩基础的加速度地震响应特性和孔压的发展曲线；李雨润等［13］进行了一系列振动台和离心振动台试验，探究了液化场地直斜群桩基础动力响应特性；SU 等［14］研究了地震作用下土体液化导致挡土墙后单桩破坏的机理，并开展振动台试验探究了液化后土体对桩身产生的侧向压力变化规律；Li等［15］在E-Defense 振动台上进行大比例尺模型试验研究，并建立了二维非线性动力有限元模型，考虑了二维有效应力情况下的桩土相互作用；LIU 等［16］开展振动台试验，针对岸壁后群桩在液化侧扩流情况下的地震响应进行了研究；Hussien 等［17］开展了一系列离心机试验研究，研究了砂土中单桩和群桩与上部结构动力响应特性，并对比了不同位置桩基的弯矩分布规律。

目前国内外学者开展多方面的桩基抗震性能的研究，但对于横向动力响应特征和影响因素的研究还不是很完善，特别是在数值模拟这一方面的研究还不够深入，大多数数值模拟分析的土体本构模型都是基于摩尔库伦模型，比较难还原真实土体的动力非线性关系，文中通过振动台试验及数值模拟对桩基础的横向动力响应的特征和影响因素进行研究，为我国桩基抗震规范提供参考提供依据，为工程建设提供理论指导。

1 试验简介

1.1 试验设备

饱和砂土液化场地中对称双直桩和对称双斜桩土-桩相互作用振动台试验在中国地震局工程力学研究所完成，采用的振动台为全数控电磁式驱动一维剪切震动模拟台，台面尺寸为1.2 m×2.2 m，振动台如图1所示；采用的传感器有FBG 光栅、孔隙水压传感器、加速度传感器，分别是用来采集桩身轴向应变、地基土孔隙水压力、地基土及承台加速度信号；为降低地基模型边界效应采用叠层式剪切箱，其尺寸为800 mm×500 mm×600 mm，如图1所示。

图1 振动台和小型剪切箱Fig.1 Shaking table and small shear box

1.2 试验模型

试验原型为桩长14.8 m，桩直径0.5 m，材料为C30 混凝土，弹性模量Ep=3.0×104MPa。试验模型设计依据Buckingham π相似设计理论，试验模型与原型几何相似比确定为1/25，试验模型相似比如表1所示。对称双桩的桩身长度590 mm，桩径为20 mm，承台尺寸为156 mm×78 mm×26 mm，承台与桩基通过套筒连接，试验模型桩选择有机玻璃（PMMA）材料，弹性模量为Ep=1.2×103MPa，模型桩表面进行打磨处理，模拟工程钢筋混凝土桩基表面粗糙度；地基土底部持力层用橡胶垫模拟，桩基插入底部橡胶垫中50 mm，双直桩模型如图2所示，双斜桩模型如图3所示。

表1 试验模型动力相似系数和相似比Table 1 Dynamic similarity coefficient and similarity ratio of test model

图2 直桩模型Fig.2 The straight pile model

图3 斜桩模型Fig.3 Inclined pile model

每组试验用到6个加速度传感器，孔隙水压力传感器4个，FBG光栅20个，双直桩工况传感器布置如图4（a）所示，双斜桩工况传感器布置如图4（b）所示。

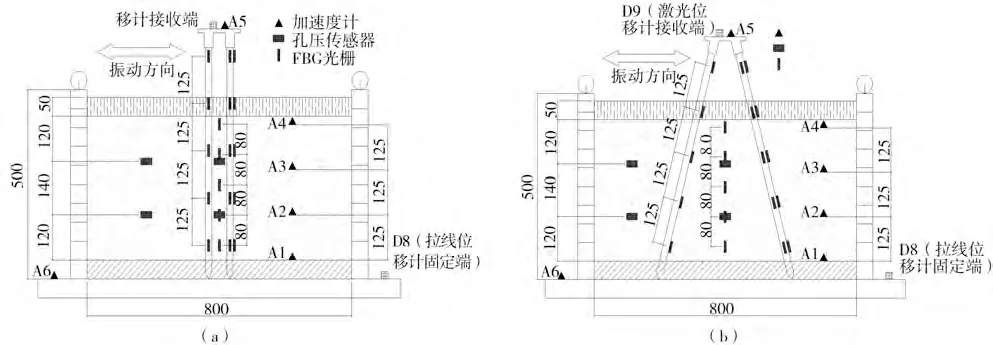
图4 传感器模型布置图Fig.4 Sensor model layout

本试验选取的动荷载为频率3 Hz峰值加速度分别为0.15 g、0.20 g、0.30 g的正弦波。动力荷载在模型箱底部输入，正弦波持时20 s，加载方向为x方向（如图4所示）。试验工况如表2所示。

表2 试验工况Table 2 Test conditions

1.3 模型建立

Yang 等［18-19］在多屈服面应力空间模型的基础上，加入了应变空间的应变率这一概念，创建了砂土液化的应力应变弹塑性本构模型，并通过CYCLIC 验证了砂土液化的应力应变弹塑性本构模型的可靠性。庄海洋等［20］在Yang Zhaohui 的砂土液化的应力应变弹塑性本构模型的基础上改进模型的硬化法则，通过开发接口在ABAQUS 平台上运行，并通过一系列动三轴单元试验和振动台模型试验验证了模型的可行性。

试验模型为对称直斜双桩模型，动力荷载的输入方向与双桩构成的平面平行，故可将数值三维模型沿振动方向简化为二维平面模型，在保证计算精度前提下有效缩减计算量提高计算效率。基于ABAQUS有限元平台二次开发功能，成功引入砂土液化大变形本构模型，在此基础上建立了动静耦合桩土相互作用二维桩-土相互作用动力简化计算模型，并采用网格自适应技术解决了地基液化大变形带来的计算不收敛问题。

为消减模型边界效应对模型试验的影响，充分发挥数值模拟灵活及低成本的优势，扩大地基土范围，选择数值模型的场地尺寸为4 000 mm×500 mm，桩基的承台尺寸156 mm×26 mm，桩基的直径为20 mm，两桩之间的距离为4倍桩径，模型试验中桩基承台与桩之间通过套筒连接，建模过程中将套筒连接简化为桩基承台与套筒之间固定连接，数值模型如图5所示。

图5 数值分析模型Fig.5 Numerical analysis model

土体为3 层土，由上到下分别是非液化黏土层（厚度50 mm）、饱和砂土层（厚度380 mm）和橡胶垫（厚度70 mm）。桩基础参数如表3所示。为实现桩-土相互作用的非线性静动耦合模型计算，整个分析过程分为静力计算、静动力转换和动力计算3个部分，在静力计算时地基模型底面采用固定约束而两边侧面是限制水平方向上的位移，然后将静荷载计算结果用于地应力平衡计算；在施加动荷载前进行边界条件转换，解除场地两侧边的水平约束并限制其竖向位移，基岩面水平方向则转换为地震波输入；设立Dynamic Implicit 计算分析步，进行动力计算。桩基础与土相互作用通过设置桩土相互作用接触实现，设定桩表面为主接触面，土的面为次接触面，主次接触面设定为摩擦接触，接触摩擦因子为0.4。试验模型中桩底插入橡胶垫模拟固端链接，数值模型中桩底通过绑定（Tie）接触与底层地基连接。

表3 桩模型参数Table 3 Pile model parameters

2 试验结果与数值模拟结果对比分析

对模型试验数据进行处理，并与ABAQUS 有限元建立的动静耦合桩土相互作用二维双桩动力简化模型的计算结果进行对比分析，验证模型的有效性，探究对称双桩横向动力响应的一般规律。由于文中篇幅有限，故选取峰值加速度0.20 g正弦波试验和数值分析结果进行分析。

2.1 干砂模型试验与模拟结果对比分析

图6～图9 分别给出了干砂中对称双直桩和对称双斜桩在峰值加速度0.20 g正弦波作用下的加速度和位移时程曲线。

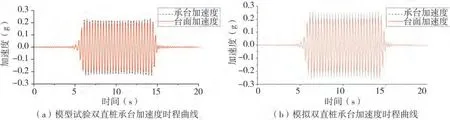
图6 0.20 g正弦波工况双直桩承台加速度时程曲线Fig.6 Acceleration time history curve of double straight pile cap under 0.20 g sine wave condition

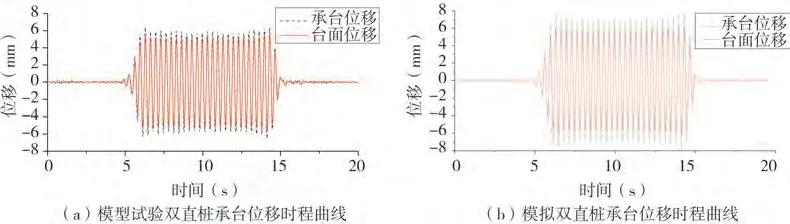
图7 0.20 g正弦波工况双直桩承台位移时程曲线Fig.7 Displacement time history curve of symmetrical double straight pile with 0.20 g sine wave input

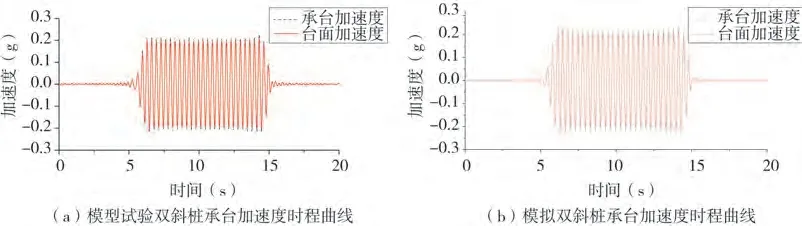
图8 0.20 g正弦波工况双斜桩承台加速度时程曲线Fig.8 Acceleration time history curve of double inclined pile cap under 0.20 g sine wave condition

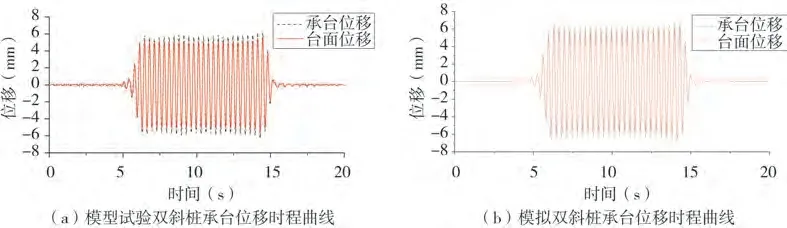
图9 0.20 g正弦波工况双斜桩承台位移时程曲线Fig.9 Displacement time history curve of double inclined pile cap under 0.20 g sine wave condition

由试验和模拟结果对比分析可以得出，承台的加速度和位移相较于振动台台面的加速度和位移有整体的放大趋势，且在整个动力荷载作用的时间段内放大的波形比较均匀，未出现较大的波动。如表4 所示，在相同荷载作用下，对称双直桩在干砂场地中的承台峰值位移和承台峰值加速度只是略大于对称双斜桩，两者的数据差距不大，对称双斜桩没有表现出较好的优势。干砂中动力荷载作用下对称双直桩与对称双斜桩横向动力响应程度相当。

表4 对称双桩横向动力响应特征参数汇总表Table 4 Summary of characteristic parameters of lateral dynamic response of symmetrical double piles

桩基进行编号如图4 所示。试验中的桩身FBG 光栅分别位于0 cm、3.3 cm、15.8 cm、28.3 cm、40.8 cm、53.3 cm、59 cm 处（以剪切箱底部内壁为0 cm 平面），通过把采集到的光信号转变成为电信号，对电信号进行处理得出桩身弯矩。对干砂中峰值加速度0.20 g 正弦波工况直斜双桩的弯矩包络图进行分析，并与数值模型计算结果对比验证，探究桩基在动力荷载作用下的最不利位置，为规范设计提供理论依据，为实际工程提供理论指导。

如图10所示，1号桩和2号桩的弯矩包络图形式基本相符，只是在数值上略有差别。试验和模拟的弯矩包络图相似，截面的最不利位置出现在桩基顶部和承台相连位置和桩尖位置，对称双直桩的试验的最大弯矩为0.153 kN·m，模拟的最大弯矩0.133 kN·m在桩顶位置，对称双斜桩试验的最大弯矩0.155 kN·m，模拟的最大弯矩为0.148 kN·m。桩基弯矩最大值出现在桩顶和桩尖，分析是桩的两端分别受到承台和下部持力层的约束，导致弯矩较大。

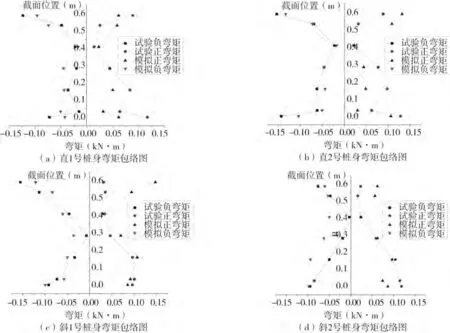
图10 0.20 g正弦波作用下对称双直桩和对称双斜桩弯矩包络图Fig.10 Bending moment envelope diagram of symmetric double straight pile and symmetric double inclined pile under 0.20 g sine wave

2.2 液化土试验和模拟对比分析

图11～图14 分别给出了液化砂土中对称双直桩和对称双斜桩在峰值加速度0.20 g 正弦波作用下的加速度和位移时程曲线。

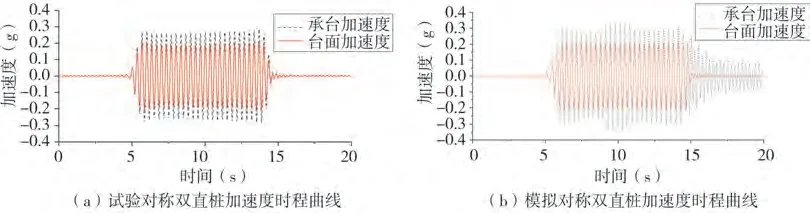
图11 0.20 g正弦波输入下对称双直桩加速度时程曲线Fig.11 Acceleration time history curve of symmetric double straight pile with 0.20 g sine wave input

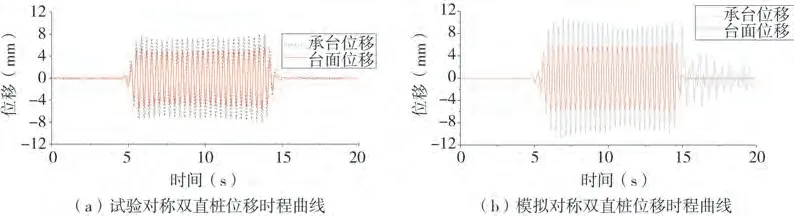
图12 0.20 g正弦波输入下对称双直桩位移时程曲线Fig.12 Displacement time history curve of symmetrical double straight pile with 0.20 g sine wave input

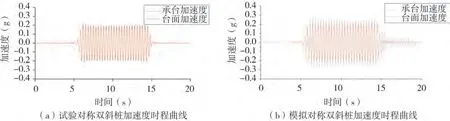
图13 0.20 g正弦波输入下对称双斜桩加速度时程曲线Fig.13 Acceleration time history curve of symmetric double inclined pile with 0.20 g sine wave input

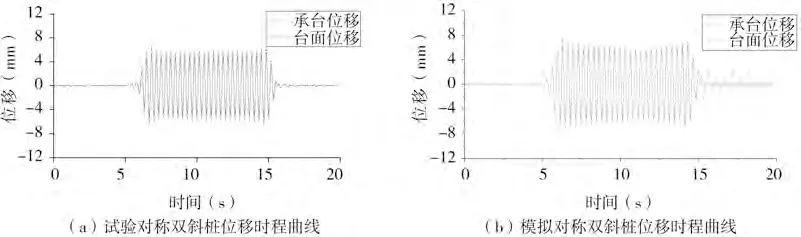
图14 0.20 g正弦波输入下对称双斜桩位移时程曲线Fig.14 Displacement time history curve of symmetric double inclined pile with 0.20 g sine wave input

通过对比对称双直桩和对称双斜桩在0.20 g正弦波作用下的横向动力响应，如表5所示，对称双直桩在液化场地中承台的位移峰值和加速度峰值以及放大倍数都比对称双斜桩的大，说明液化砂土中对称双直桩的横向动力响应更加显著，对称双斜桩在液化场地中的适应性更好。原因是沿着x方向输入正弦波，桩上土的反力一部分被分解为了沿着斜桩轴向的力，从而减小了位移峰值和加速度峰值。

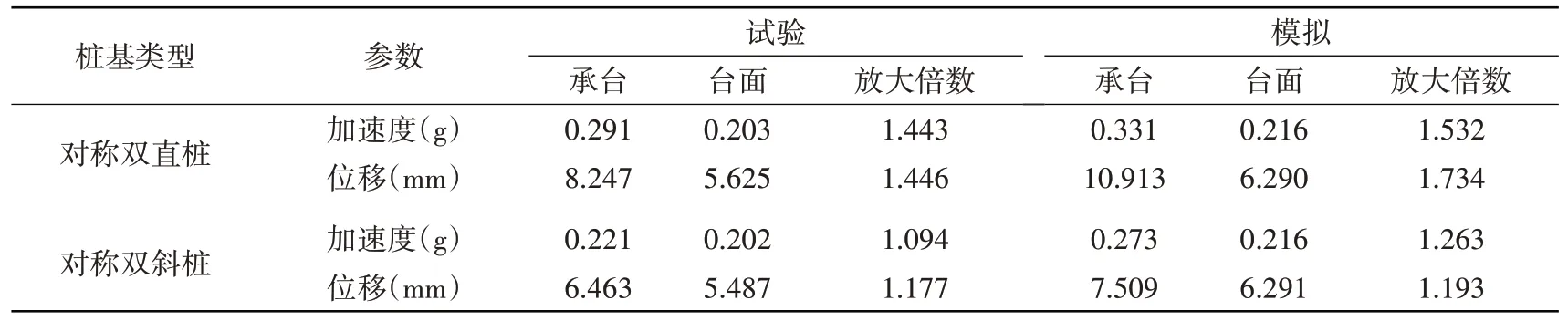
表5 对称双桩横向动力响应特征参数汇总表Table 5 Summary of characteristic parameters of lateral dynamic response of symmetrical double piles

通过数值模拟输出超静孔压比云图，如图15、图16所示，图中浅色部分为超静孔压比达到1.0部分，采用的砂土大液化本构编写的UMAT子程序输出超静孔压比代号为（SDV52），当超静孔压比达到1.0时认为砂土已经液化。

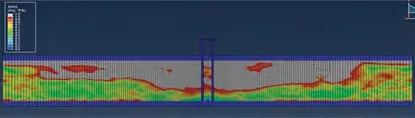
图15 0.20 g正弦波作用下对称双直桩超静孔压比云图Fig.15 Overstatic hole pressure ratio cloud diagram of symmetrical double straight pile under 0.20 g sine wave

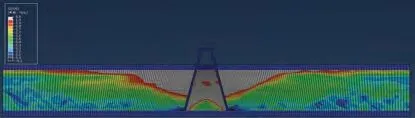
图16 0.20 g正弦波作用下对称双斜桩超静孔压比云图Fig.16 Overstatic hole pressure ratio cloud diagram of symmetric double inclined pile under 0.20 g sine wave

场地液化的发展是从土体浅层向深部发展，符合砂土液化的机理，深层土体还未发生液化，0.20 g 正弦波对地基上层的土体影响范围较广，中上部地基几乎全部液化，从图中反映出，近桩砂土层从上往下超静孔压比出现逐渐增大的趋势，远桩场地规律相似，桩基附近的土体受到桩基的影响，同一深度近桩地基土的孔压发展比远桩地基土孔压发展更快，原因是离桩更近，桩对孔压的影响更大，有利于超静孔压的发展。称双斜桩对砂土地基的影响更大，两桩之间的砂土液化发展很快，远场地基只发生了轻微液化，场地的液化情况基本上是沿着桩中心对称的。

在模型试验中设计了孔压传感器采集土层中的孔隙水压力的发展情况，分别布置了上下两层孔压传感器，每层两枚孔压传感器，分别位于桩间和桩外靠近剪切箱内壁的位置。实时监测动力荷载作用下的孔压变化，试验中对称双直桩和对称双斜桩的超静孔压时程曲线相当，且不同工况下砂土液化过程中的超静孔压时程曲线发展趋势相同，只是在数值上有所差异，故文中仅选择0.20 g正弦波作用下对称双直桩孔压时程曲线进行分析。

由图17 可得，孔压在6 s 左右急剧上升，迅速达到1.0，表示该土层已经液化，试验中液化砂土的孔隙水压力大于砂土颗粒自身重力，导致砂土层和上部黏土层软化，当孔隙水压力大于上覆时，地下水携带砂土颗粒喷涌而出，试验可观察到“喷水冒砂”现象，在试验结束后桩基附近黏土出现开裂现象，如图18所示。从试验孔压可以看出，上层的超静孔压比要略大于下层的超静孔压比，外侧孔压波动较大，经分析是外侧孔压传感器靠近层状剪切箱的内壁，动力荷载由于边界效应在边界处产生干涉或衍射叠加所造成的，试验孔压比在达到1.0后，稳定了10 s左右，然后迅速下降，逐渐消散到0.2左右，上层孔压的消散要略快于下层孔压，符合孔压向上传递的机理；从模拟孔压可以看出，上层的内侧孔压要大于外侧孔压，结合图16 分析可得，桩间上层的土体受桩的影响较大，先于远桩液化，符合试验数据。

图17 0.20 g正弦波作用下对称双直超静孔压时程图Fig.17 Time history diagram of symmetrical double straight overstatic pore pressure under 0.20 g sine wave

图18 试验现象Fig.18 The test phenomenon

桩基的编号与干砂中的桩基编号相同，将靠近伺服电机一侧的桩编号为1号桩，将远离伺服电机一侧的桩编号为2号桩。

从图19 的结果可以看出，对称双桩的1 号桩和2 号桩的弯矩包络图形式基本一致。对称双直桩的试验中桩基的弯矩最大值出现在桩顶，1 号桩的最大负弯矩达到了0.879 kN·m。数值模拟的桩基弯矩最大值1.399 kN·m 出现在桩尖处。对称双斜桩的试验和数值模拟的弯矩包络图都为“花瓶状”，数值模拟和试验的趋势相似，数值上差距不大，试验的弯矩最大值1.166 kN·m出现在桩顶与承台连接处，数值模拟的弯矩最大值1.504 kN·m出现在桩基中下部位。

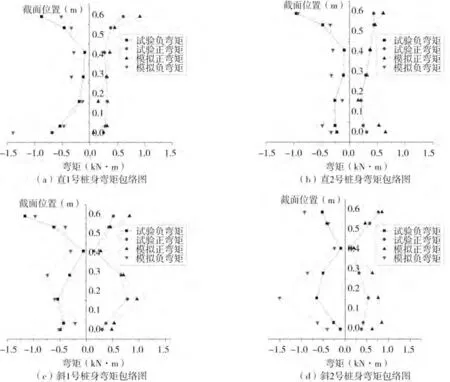
图19 0.20 g正弦波作用下对称双直桩和对称双斜桩弯矩包络图Fig.19 Bending moment envelope diagram of symmetric double straight pile and symmetric double inclined pile under 0.20 g sine wave

3 结论

通过对称双桩的动力响应振动台试验，分析了0.20 g正弦波输入下，对称双直桩和对称双斜桩的横向动力响应特征，并基于砂土液化大变形本构模型在振动台试验的基础上进行了数值模拟分析，将试验数据和数值模拟分析数据进行对比验证，验证数值模型的有效性和准确性，同时对比分析，得出了以下结论：

（1）干砂中对称双直桩与对称双斜桩横向动力响应程度相当，液化砂土中对称双直桩的横向动力响应更加显著，对称双直桩承台的位移峰值和加速度峰值均大于对称双斜桩，说明对称双斜桩具有更强抵御水平动力荷载的能力和抗倾覆能力，在液化场地中的适应性更好。

（2）在液化场地中，砂土的液化是从土层浅层向下发展的近，同一深度近桩地基土的孔压发展比远桩地基土孔压发展更快，原因是离桩更近，桩对孔压的影响更大，有利于超静孔压的发展，故桩基周围土体要比远桩土体先液化。

（3）分析孔压时程图，在液化过程中，超静水压力的发展分为上升、稳定、消散3个阶段，孔压的消散是沿着四周向上消散的，故上层孔压的消散要略微滞后于下层孔压，且上层孔压要大于下层孔压。

（4）动力荷载输入下，对称双桩的1 号桩和2 号桩的弯矩包络图分布相似，干砂中对称双桩的弯矩最大值均出现在桩顶和桩尖位置，而液化砂土中对称双直桩的桩身最不利截面在桩顶和桩尖位置，对称双斜桩的桩身最不利截面位置发生变化，桩顶位置和桩中下部皆有分布；场地液化使桩身最大弯矩放大10倍以上，同一工况作用下斜桩的最大弯矩比直桩的最大弯矩更大，说明在地震中砂土液化后，斜桩承受的弯矩更大。