人工智能对交通效率的影响
2022-09-22付书凡王慧敏毕婧
付书凡 王慧敏 毕婧
(沈阳师范大学软件学院 辽宁沈阳 110034)
人工智能日趋成熟,自动驾驶系统在提高道路通行能力、改善车辆主动安全性等方面具有巨大潜力。自动驾驶车辆在道路上所占的比例不同,会对道路的交通效率产生不同程度的影响。
在不同的交通网络中,交通效率各有不同,在自动驾驶汽车登上公路时,会对交通效率产生一定的影响。自动驾驶的比例不同,可能会加快交通效率,也可能会导致交通效率变慢甚至瘫痪。因此,做出以下分析:探究在拥堵系数、汽车行驶速度、道路干扰、汽车种类方面,车流中自动驾驶比例对交通效率的影响;在一个由主干道、次干道、交叉路口、弯道构成的有边界的简单交通网络中,车流中自动驾驶车辆比例对交通效率的影响。
1 理论及方法
将影响因素分为两大类:即路况指标和性能指标。影响路况的指标因素有道路干扰和拥堵系数;影响性能指标的因素有行驶速度和汽车种类。
采用层次分析法来对4 个影响因素进行判断,通过建立层次模型并求解,对得出的结果进行一致性判断。使用模糊综合评判模型进行求解,通过两种方式求解最终得出结论:道路干扰和行驶速度分别是决定路况指标和性能指标的重要因素。
设定一个简单的交通网络,研究车流中自动驾驶车辆比例对交通效率的影响。据此,需要建立一个元胞自动机模型。
通过选定交通网络,又细分为十字路口、直行道和转弯等情况,针对不同的情况,对车流量进行了交通仿真模拟。通过车辆加速、减速、停止3种情况进行速度分析,通过对语句调控来设置道路口的红绿灯。通过随机概率来设定汽车直行左转右转的概率进行分析建立模型。通过在模型中明确车流量的变化、车速及红绿灯等因素,建立起比较精准的模型,进而对模型进行验证。
2 实验
2.1 建立层次结构模型
2.1.1 层次结构模型
层次结构模型如图1所示。目标层M是自动驾驶车辆比例对交通效率的影响评价体系;中间的准则层C 路况指标和性能指标;最下面的方案层P 的影响因素为道路干扰、拥堵系数、行驶速度及汽车种类。
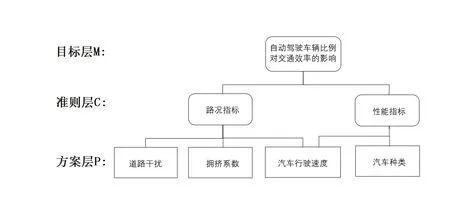
图1 层次结构模型图
2.1.2 根据建立的模型求解
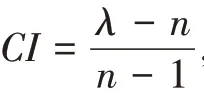
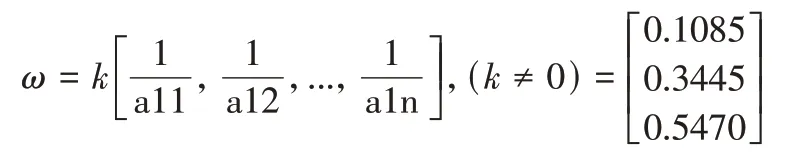
由此可求得一致性指标=0.0268,一致性比例=0.516。
因为<0.10,所以该判断矩阵的一致性可以接受。
权重向量=(0.1000 0.3500 0.5500)。
求解判断矩阵C2-P 的权重向量=(0.7500 0.2500)。
最后用层次分析法得出如表1所示关系表。
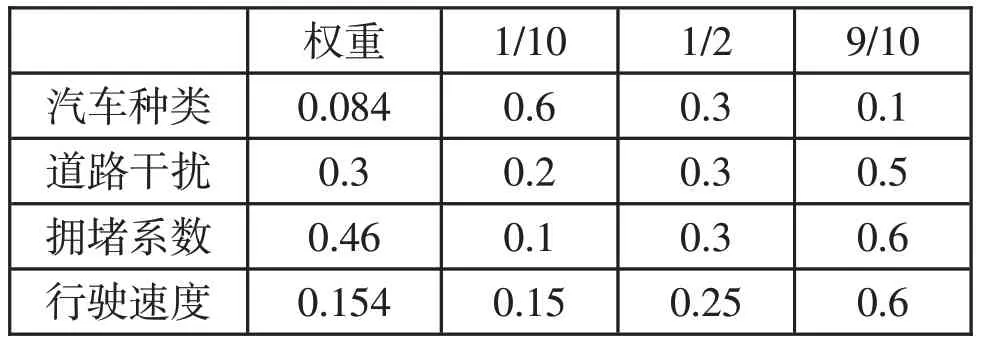
表1 自动驾驶车辆比例对交通效率影响
由表1可分析得出不同交通条件下自动驾驶车辆对交通效率的影响结果。
(1)当自动驾驶车辆在行驶车辆占比为1/10时:
影响比例=0.0504+0.06+0.046+0.0231=0.1795
(2)当自动驾驶车辆在行驶车辆占比为1/2时:
影响比例=0.084× 0.3+0.3× 0.3+0.46× 0.3+0.154× 0.25=0.2917
(3)当自动驾驶车辆在行驶车辆占比为9/10时:
影响比例=0.084× 0.1+0.3× 0.5+0.46× 0.6+0.154× 0.6=0.5268
由计算结果可知,在不同条件因素影响下,自动驾驶汽车比例越高,交通效率就越高。
2.2 建立模糊综合评判模型
“模糊”(Fuzzy)从字义上理解包含“含糊”“不确定”的概念。模糊理论(Fuzzy Theory)是建立在模糊逻辑(Fuzzy Logic)基础之上,描述和处理人类语言所特有的模糊信息的理论。它的主要概念包括模糊集合(简称模糊集)及其隶属函数、模糊算子和模糊关系。
模糊综合评价法是一种基于模糊数学的综合评价方法。根据模糊数学的隶属度理论,把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。它具有结果清晰、系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
(1)建立评判对象因素集,表示由影响判断对象的因素组成的合集。=[,,,],其中,为拥堵系数,为汽车种类,为道路干扰,为行驶速度。

(3)建立权重集,=[0.084,0.46,0.3,0.154](此数值由以上层次分析法求得)。
(4)确定模糊判断矩阵。调查单因素评价隶属度向量,并形成隶属度矩阵(模糊判断矩阵),对本题假设取4组评判。
(5)进行模糊综合模式识别,得到评判指标,=×。
(6)取中数值的最大值代表综合评判的最终结果。
2.3 基于元胞自动机模型对交通网络进行分析
元胞自动机的特点是时间、空间、状态都离散,每个变量只取有限多个状态,且其状态改变的规则在时间和空间上都是局部的。在探究自动驾驶技术所占比例对交通效率的影响中,设定了一个拥有主干道、转弯、十字交叉路口的简单交通网络,将其分为三部分,对其进行道路交通流的分析。交通流是指在道路交通系统中有关交通流参数的定性和定量特征,以及它们在不同的时空条件下的变换规律和相互关系。交通流的参数:有一些描述和反映一些交通流特性的物理量,包括行车速度、交通密度、交通量、交通延误、时间占有率等参数。由题意可知,主要选取交通密度和行车速度作为参数。
首先设置了道路上车的最初数量为200 辆,最大速度为Vmax,并记录了车的实时速度velocityv 和车辆位置(i,j),并通过判断当前位置是否为空来决定车辆是加速、减速,还是随即慢化,然后更新车辆速度,并记录更新后的车辆位置,得出了一个流量密度图和时空图。
加速过程:velocity(i-j+1)=min(velocity(i-j+1)+1,Vmax)。
减速过程:velocity(i-j+1)=min(velocity(ij+1),d)。
随机慢化:velocity(i-j+1)=randslow(v(i-j+1));new_velocity=velocity(i-j+1)。
更新位置:z(i-j+1)=0;z(i-j+1+new_velocity)=1。
更新速度:velocity(i-j+1)=0;velocity(i-j+1+new_velocity)=new_velocity。
通过相关代码运行,得到如图2 所示的流量密度图。
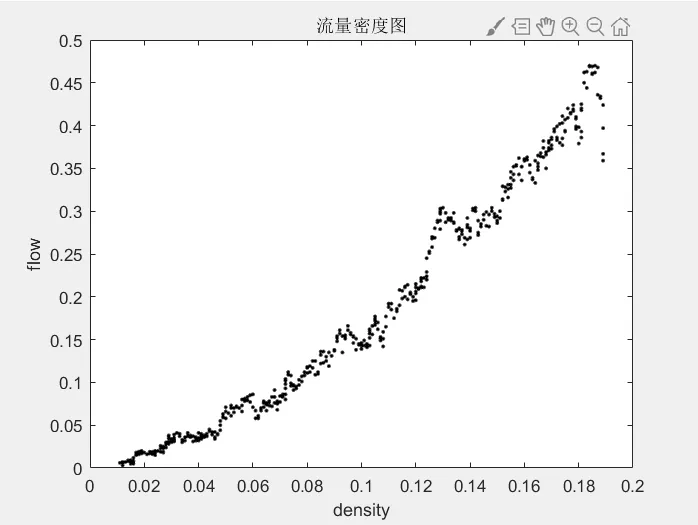
图2 流量密度图
通过基于元胞自动机的车流模型,可以看出不同速度下车辆的密度和流量。
在最初通过元胞自动机原理和直行单行道代码模拟,建立了一个直行单行道道路交通模拟模型。设直行进入研究区域的车辆的驶入概率为pp,道路长度为length,执行的步长为n。设置pp=20,long=500,n=1000,然后用flaggg判断是否有车辆在等待区即将离开区域。
设置编号为1、2、3、4的4条道路,依次为十字交叉路口之前的直行道路、左转道路、十字交叉路口之后的直行道路及右转道路。通过相关if语句调控来设置道路口的红绿灯,并通过随机概率来设定汽车直行左转右转的概率。
建立一个在特定车流密度下的双车道T型仿真模型。设定车道数目num 值为2,车道长度len 通过后期运行代码输入参数,设车辆的平均速度av、车流密度w数值、仿真步长时间ft、仿真步长数目fnum、车道入口处新进入车辆的概率向量fp、交叉口处车辆行为的概率向量q 等值,均在运行代码时输入相应的参数。据此构造元胞矩阵,设置不可行车道,并把仿真元胞状态初始化,设值为1时表示无车,为0时表示有车,然后显示初始交通流图,给变量初始化,确定车辆的状态,最终得到交通流图。
3 实验结果及分析
通过构造出表2 中的比较矩阵,为了确保权重的值更加准确,采用了算术平均法、几何平均法、特征值求法3种方式求解权重,发现3种方法求出权重的值误差很小,并对取得的权重的值进行一致性检验,将求得的一致性指标与随机一致性指标进行对照,发现符合一致性可以接受,由此得出结论:当自动驾驶车辆在行驶车辆占比分别为1/10、1/2、9/10 时,对交通效率的影响比率分别为0.1795、0.2917、0.5268。
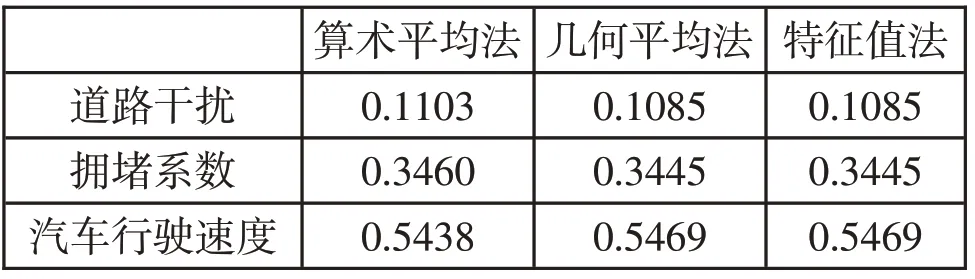
表2 3 种方法下的权重值比较
设定车辆最初数量为200 辆,并通过元胞自动机建立了车辆流量密度和超时图。
直行单行道道路和直行交叉口道路及双车道T型双车道交通,最后得到了交通流图。通过对单行道路和直行道路以双车道道路的交通流图的分析,得出结论:自动驾驶车辆比例越多,交通效率就越高。
4 改进方向
(1)本文求解问题中所用到的数据皆是通过查阅有关资料进行和分析得出的数据,具有较高的精确性,根据该数据,最后得出自动驾驶比例对交通效率的影响。
(2)在所用到的层次分析法计算权值时,采用了3种不同的计算方法求得,最后取平均值,得出权值数据更为准确。
(3)由于层次分析法定性成分过多,可能不够精准,于是还建了模糊综合评判法,能对蕴藏信息呈现模糊性的资料作出比较科学、合理、贴近实际的量化评价。
(4)在对交通网络进行模拟时,建立了离散动力学系统的元胞自动机模型,该模型具有较高的仿真能力,更真实地模拟现实交通网络。
