道路几何设计对车辆行驶特性影响机理研究

杨露

（新疆石河子职业技术学院 新疆石河子 832000）

近几年，道路交通事故呈高发态势，与车辆行驶轨迹、速度具有密切的关系，而车辆行驶轨迹受道路几何设计的直接影响。当前，道路几何设计多以汽车在运动学领域的最小安全性要求为基准，以车辆行驶过程中无外界干扰为前提，道路几何设计与车辆实际驾驶过程的偏差不可避免。因此，研究道路几何设计对车辆行驶特性的影响机理，对于道路几何设计优化具有非常重要的意义。

1 驾驶员操纵汽车行驶的轨迹决策模型构建

驾驶员操纵汽车行驶的轨迹决策模型是现实环境中汽车驾驶人员操纵能力的数学化表达。模型的重点是道路几何线形对车辆行驶特性的影响机理，需要基于预瞄最优曲率模型与SK道路几何模型，输入汽车驾驶员预期行驶轨迹信息，以实际道路几何线形中驾驶人员方向控制为重点，进行计算机仿真程序编制。

1.1 预瞄最优曲率模型

预瞄最优曲率模型将汽车驾驶人员控制汽车方向的策略划分为2 个阶段：第一个阶段是根据所感受的前方道路信息、汽车当前运动状态，落实汽车行驶轨迹、预期行驶轨迹偏差处于最细微水平的方针，确定最优侧向加速度；第二个阶段是汽车驾驶人员根据汽车静态与动态特殊表现，控制方向盘转角，确保汽车实际行驶轨迹与预瞄行驶轨迹无偏差。假定瞬时时间内汽车即时状态=（），则汽车最优行驶轨迹曲率为：

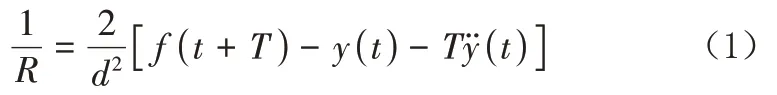
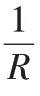
由于汽车驾驶人员存在反应滞后性，驾驶人员的理想方向盘转角、实际方向盘转角并不完全冲抵，此时，可以利用一个传递函数表示汽车驾驶人员的反应滞后性与实际方向盘转角之间的关系，即：

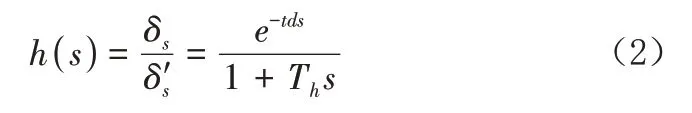
式中：为距起点曲线长度（m）；δ为实际方向盘转角（°）；δ′为理想方向盘转角（°）；为神经反应滞后时间（s）；表示距起点曲线长度范围内神经反应滞后时间的幂次方；T为手臂反应滞后时间（s）。

在多数汽车方向盘无突然变更的驾驶场景中，即便是高速行驶的汽车也不涉及汽车的动态响应问题，此时，汽车方向盘的运动服从Acklman几何关系，汽车行驶轨迹曲率、方向盘转角呈正相关。

1.2 SK道路几何模型

SK道路几何模型主要是用桩号（S）、曲率（K）统一表示道路的平面几何线形。在SK道路几何模型中，道路的平面几何线形可看作直线、圆曲线、缓和曲线3个线元组成的曲线链，具体表达如下：

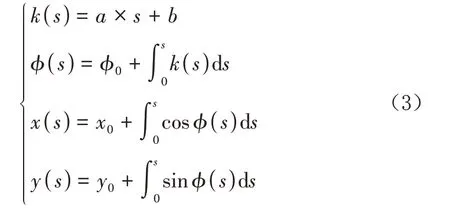
式中：（）为距起点曲线长度为位置曲率；()为距起点曲线长度为位置方位角；（）为距起点曲线长度为位置横坐标；（）为距起点曲线长度为位置纵坐标；、为任意常数；为曲线起点位置方位角；为曲线起点位置横坐标；为曲线起点位置纵坐标。

2 道路几何设计对车辆行驶特性的影响因素

作为一种三维带状空间结构，道路几何线形设计包括平面线形、纵断面线形两种。各线形要素存在较大差异，对汽车行驶特性的影响也有所区别。

2.1 平面线形

2.1.1 圆曲线

圆曲线是道路出于改变路段方向、适应地形、确保线性美观与连续需要而设计的线性，对道路交通安全影响较大。因汽车进入圆曲线、驶离圆曲线时速度变化幅度较大，圆曲线起点、终点位置交通事故发生概率较高。特别是小半径圆曲线，驾驶人员遇突发事件时操作出错率较高，极易导致连带交通事故的发生。同时，随着圆曲线曲率的增加，道路安全事故发生率也会增加，这主要是由于道路圆曲线曲率增加致使汽车行驶过程中转弯半径缩小，承受的横向压力增大，一旦汽车所承受的横向压力超过轮胎与地面的摩擦阻力，就会导致汽车出现侧滑事故。除此之外，道路圆曲线曲率增加也会导致行驶期间视觉盲区增大，埋下安全隐患。

2.1.2 直线

直线是道路平面几何线形设计中应用频率较高的线性，兼具距离短、速度快、受力简单的优势。由道路交通事故统计情况可知，直线长度与道路交通事故发生率、事故损失呈正相关。这主要是由于道路直线较长时，视觉参照物减少，易致使汽车驾驶人员注意力分散，影响车辆之间距离目测准确度，在遇到突发事件时，神经滞后性较为突出，加之在长直线道路中，汽车驾驶人员会不自觉提高车辆行驶速度，且在驾驶距离较长时疲乏感加重，增加了交通事故发生风险。

2.2 纵断面线形

2.2.1 最大坡长

道路纵断面线形中最大坡长涉及上坡最大坡长、下坡最大坡长两个部分。上坡最大坡长与汽车行驶期间换挡频率呈正相关，过大的上坡最大坡长会增加汽车驾驶人员的心理负担，并致使汽车发动机温度、水箱温度及汽油损耗处于较高水平，甚至致使汽车熄火后轮胎与路面滑动，增加风险发生概率。同时，过大的上坡最大坡长也会干扰车辆驾驶人员对道路坡度的判断，最终出现错误的车辆驾驶行为，埋下事故隐患。

下坡最大坡长与车辆行驶速度呈正相关。过大的下坡最大坡长需要车辆驾驶人员持续踩踏制动器，加重刹车片磨损，甚至引发制动失效；而过小的下坡最大坡长将致使变坡点增加，干扰道路平顺性。

2.2.2 最大坡度

道路最大坡度是纵断面线形的主要元素，与交通事故发生率呈正相关。特别是在道路纵断面最大坡度在4%以上时，受车辆自身重力、惯性力影响，汽车加速度与速度持续朝着高水平发展，在汽车速度处于较高水平时，行车事故的发生概率也较高。同时，最大坡度对汽车爬坡能力也具有一定影响，间接影响汽车行驶速度，此时，不同车辆在爬坡过程中速度差距的拉大将致使超车、追尾事故高发。

3 道路几何线形设计方案

3.1 平面线形设计方案

在道路几何线形设计过程中，直线最长距离与最大设计车速有关，一般需要小于最大设计车速在3min内行驶的距离。缓和曲线多选择回旋线，一般长度为150m，以促使汽车以一定速度由直线驶入圆曲线或者由圆曲线驶入直线的轨迹相当，降低汽车驾驶人员操作难度。而对于平曲线，需要控制曲线半径大于40m、小于100m，且道路偏角大于7°，避免行车事故出现。

3.2 纵断面线形设计方案

在最大坡长设计时，设计人员应保证竖曲线长度超过最大设计车速在3min内的行程。同时，设计人员应考虑立交匝道位置、交通标志位置与车道变化位置让驾驶人员神经滞后情况，增加2.5s 以上的判断时间行驶车程。

在额定满载功率比为9.0kW/t时，最大纵坡与设计速度有关。在车辆行驶速度为120km/h 时，最大纵坡为3%；在车辆行驶速度为100km/h 时，最大纵坡为4%；在车辆行驶速度为80km/h 时，最大纵坡为5%；在车辆行驶速度为60km/h时，最大纵坡为6%；在车辆行驶速度为40km/h时，最大纵坡为7%；在车辆行驶速度为30km/h 时，最大纵坡为8%；在车辆行驶速度为20km/h 时，最大纵坡为9%。从道路通行能力来看，道路在达到其基本通行能力时的运行速度一般为设计速度的一半，为保证道路基本通行能力，汽车最低运行速度应与基本通行能力相应的速度相等。即在纵坡为3%时，车辆运行速度为68km/h；在纵坡为4%时，车辆运行速度为58km/h；在纵坡为5%时，车辆运行速度为52km/h；在纵坡为6%时，车辆运行速度为45km/h；在纵坡为7%时，车辆运行速度为38km/h；在纵坡为8%时，车辆运行速度为30km/h；在纵坡为9%时，车辆运行速度为21km/h。例如，某设计为100km/h的道路（含1600m互通式立交主线），受现有道路、河流的限制，互通区需克服高差20m，平均纵坡2.5%，无法满足互通主线纵坡要求，此时，可以将纵坡划分为两个路段：前800m为主线减速期，坡度为3.0%；后800m为主线汇流加速区，坡度为2%。

4 道路几何设计对车辆行驶特性的影响验证

4.1 圆曲线半径对车辆速度安全性影响

在车辆驾驶人员初始期望速度为80km/h、预瞄距离为200.0m、直线长为120m、纵坡与缓和曲线长均为150m、纵坡度为2.5%、神经滞后时间为0.05s、预瞄间隔为2.0m、预瞄时间为2.0s时，以车速变化系数为指标进行道路圆曲线半径变化对车辆行驶特性的影响验证。车速变化系数为：

式中：为第+1 路段汽车行驶速度；为第路段汽车行驶速度。将式（1）、式（2）、式（3）、式（4）在Carsim软件中整合，得出结果如表1所示。

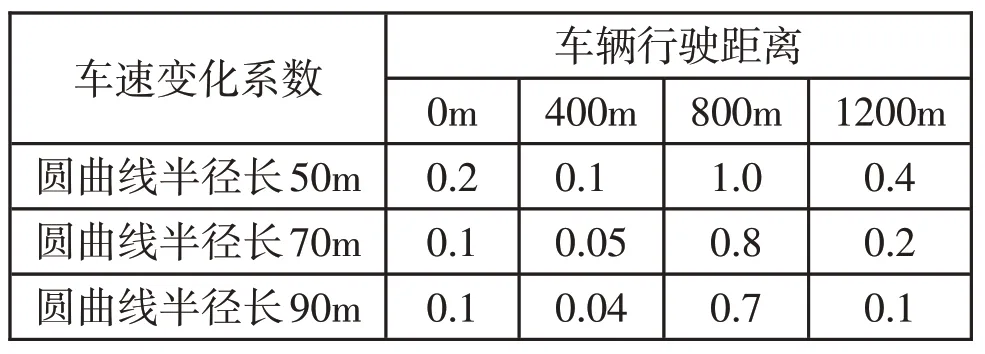
表1 不同圆曲线半径下车速变化系数

由《汽车操纵稳定性试验方法》（GB/T 6323-2014）可知，普通汽车速度变化系数≤0.5表明安全等级较高，＞1 表示安全等级较差。根据表1结果可知，车速变化系数均在1.0 以内，可以随着道路线性的变化而变化，满足车辆安全行驶要求。根据车辆行驶速度变化系数，可以设定圆曲线半径为90m。同时，在车辆行驶距离达到800m，受道路曲率影响，车速变化系数急剧增加，后期，可以通过在路段前增设减速牌或减速带，提醒车辆驾驶人员降低车辆行驶速度。

4.2 最大纵坡度对车辆速度安全性影响

在不考虑某一时刻车辆实际行驶轨迹、预期行驶轨迹侧向偏差——行车轨迹侧向偏移量的情况下，假定道路缓和曲线长、直线长、纵坡长一定的情况下，研究道路最大纵坡度对车辆速度安全性的影响，得出结果如表2所示。

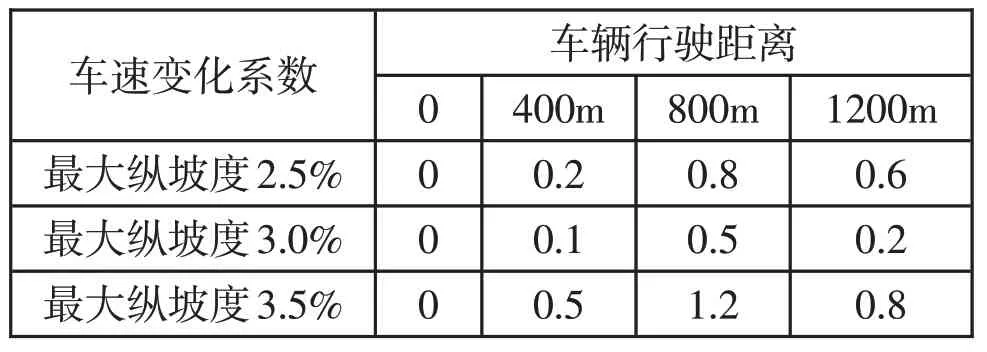
表2 不同最大纵坡度下车辆速度变化系数

在最大纵坡度达到3.5%时，车辆速度变化系数超过1.0，安全风险较大；在最大纵坡度为3.0%时，车辆速度变化系数较小，可满足安全行驶需要。

5 结语

综上所述，基于现实道路行驶条件构建的车辆驾驶人员操纵汽车行驶轨迹决策模型由预瞄最优曲率模型、SK道路几何模型组成，满足汽车运动的Acklman几何关系。在模型构建后，可以根据SK道路几何模型内求得的缓和曲线长度、曲线半径、初始方位角、起点坐标等道路平面线形设计参数，明确预定时间段汽车行驶轨迹中心线，进而经坐标变换，利用与车辆方向相一致的相对坐标系代替绝对坐标系。因汽车驾驶人员所预瞄的信息为车辆前方一段距离内道路信息，对应的输入量应为相对坐标下道路信息与提前量的乘积，提前量是前视时间内对应的道路几何线形信息，由此，可根据最小误差原则，确定最优汽车行驶曲率及对应的方向盘转角，进而根据汽车运动的Acklman几何关系，以线性几何参数为输入量，输出汽车侧向加速度、速度数据，确定汽车行驶速度变化系数，为道路几何线形的优化提供依据。