考虑界面应力分布不均匀影响的挡土墙主动土压力分析方法

王 峰，曹文贵

（湖南大学土木工程学院, 湖南 长沙 410083）

挡土墙土压力的计算一直是土木、水利等学科重要的研究课题。经典的朗肯土压力理论和库伦土压力理论因概念清晰、计算简单而得到广泛应用，但其计算得到的土压力线性分布与实际工程不符。大量的现场观测与室内试验[1-5]发现，挡土墙后土压力呈非线性分布，且与挡土墙的位移模式和墙土摩擦角有关。目前，关于挡土墙土压力计算的研究，大多采用水平分层单元进行受力分析。关于计算单元上分布荷载的分析，是计算挡土墙土压力的关键，而这也正是本文研究的出发点。

卡岗于1960年首次提出水平分层计算法，并由此得出土压力非线性分布的计算结果，但其未考虑墙背摩擦对土压力计算结果的影响[6]。对此，Handy 等[7]、Paik 等[8]在水平分层计算方法的基础上引入主应力迹线概念，借助主应力迹线描述墙后土体的应力状态，以表征墙背摩擦对墙后土体应力状态的影响。之后，国内外众多学者[9-18]在Paik 等[8]研究的基础上进行了改进和推广。应宏伟等[9]通过对墙后土体主应力迹线的形状进行分析，证明了主应力迹线形状对土压力分布的影响很小，并建议采用形状相对简单的圆弧进行分析。章瑞文等[10]指出在忽略水平剪切应力的情况下，计算单元并不满足静力平衡条件，并据此对滑裂面的倾角进行了重新计算。Xie 等[16]和Khosravi等[17]考虑曲线滑裂面，得到了土压力分布的有限差分解。涂兵雄等[18]通过应力坐标平移的方法，将水平分层计算方法推广到黏性填土挡土墙土压力计算中。但在这些研究中，一般需要通过假设计算单元界面上的竖向正应力和水平剪切应力均布分布才能实现土压力的求解，这显然与实际情况不符。竖向正应力和水平剪切应力作为分布在计算单元界面上的界面应力，对土压力计算有着重要影响，目前研究中关于其作用效果的讨论也相对甚少。

针对以上不足，本文在前人关于墙后土体应力分布及主应力偏转规律研究的基础上，采用楔体单元进行受力分析，将界面不均匀分布的剪应力和正应力等效为作用在楔体单元边界上的集中力即合力，并根据楔体单元的静力平衡条件，建立了可以考虑单元界面剪应力和正应力不均匀影响的挡土墙主动土压力计算的新方法。最后，通过对比验证了本文方法的可行性和合理性，并进一步探讨了界面应力对土压力计算结果的影响，对现有的研究进行了补充。

1 基本假定

鉴于挡土墙工程实际情况的复杂性，为了本文研究的方便，如图1 所示，对实际工程进行简化，并作如下假设：

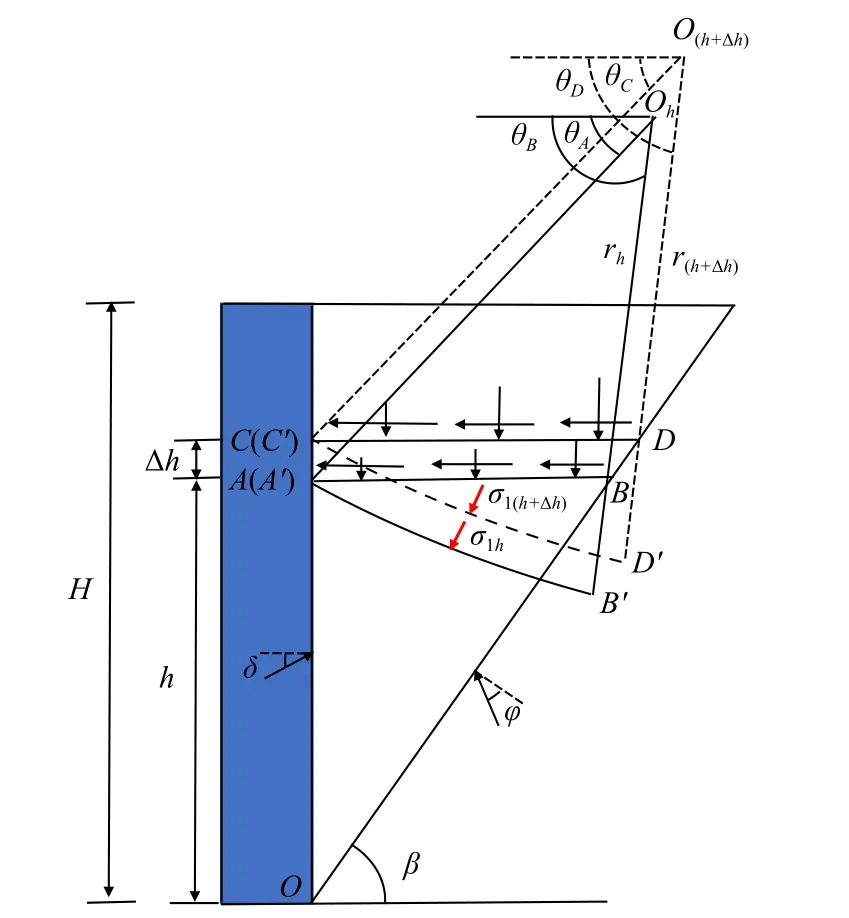
图1 滑动楔体及主应力迹线示意图Fig.1 Schematic diagram of the sliding wedge and principal stress trace

（1）挡土墙墙高H；墙背竖直粗糙，且与填土之间的接触摩擦角为 δ；填土面水平，不考虑地面超载作用。

（2）墙后墙土为无黏性土，其内摩擦角为 φ。

（3）考虑主动破坏模式，假定墙后填土内部形成通过墙踵的潜在滑裂面，滑裂面倾角为库伦滑裂面倾角 β[6]，则：

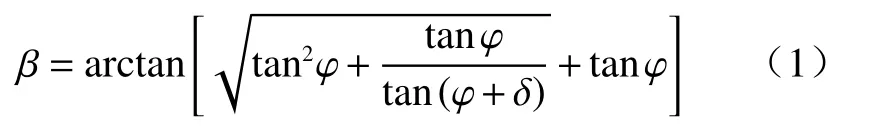
2 墙后土体应力状态分析

考虑土拱效应影响，墙后土体的应力状态发生改变。如图1 所示，水平面AB和CD上的所有土体，其应力分布符合Paik 等[8]的假设：土体强度完全发挥，小主应力迹线A'B'和C'D'为圆弧，且大小主应力的大小沿水平面保持不变。由于土拱效应的影响，水平面AB和CD上存在不均匀分布的竖向正应力和水平剪切应力，并且此时AB面和CD面上土体大主应力的大小不再等于上覆土层的自重应力，而是一个未知量，分别用 σ1h和σ1(h+Δh)表示。

如图2 所示，对墙背处A点进行应力分析。通过分析，可得墙背处A点的小主应力迹线圆心角 θA为：

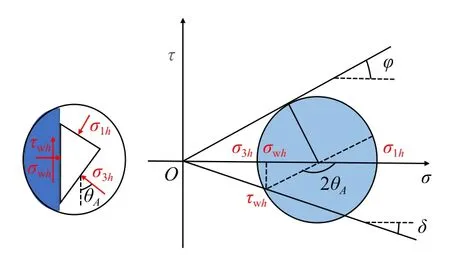
图2 墙背A 点处土体应力状态分析模型Fig.2 Analysis model of the soil stress state at point A on the back of the wall

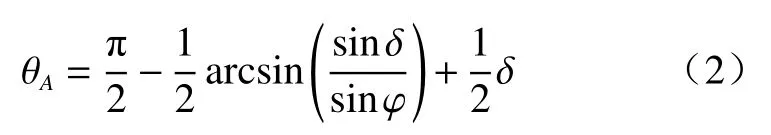
A点处土体竖直方向上作用的水平正应力，即高度h处的土压力强度 σwh为：

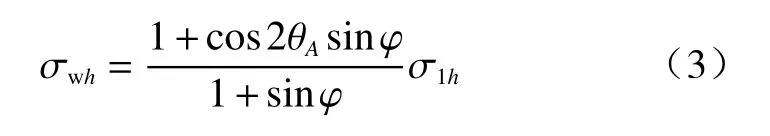
假设AB面上某一点处的小主应力迹线圆心角为θ，则该点水平方向上作用的竖向正应力 σvh和水平剪切应力 τhh分别为[12]：

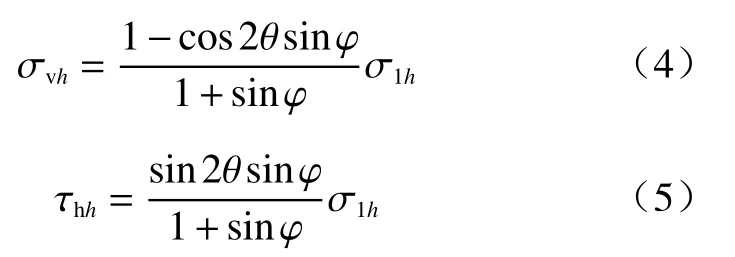
滑裂面处B点小主应力迹线圆心角 θB为[12]：

小主应力迹线A'B'的半径rh为：

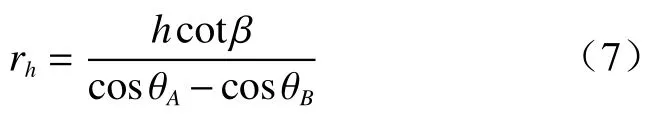
将AB面上所有土体水平方向上作用的竖向正应力和水平剪切应力沿AB面进行积分，可得到作用在AB面上竖向正应力的合力Fσh和水平剪切应力的合力Fτh分别为：

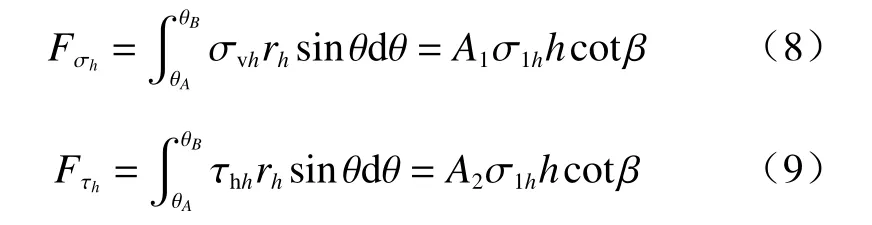
式中：

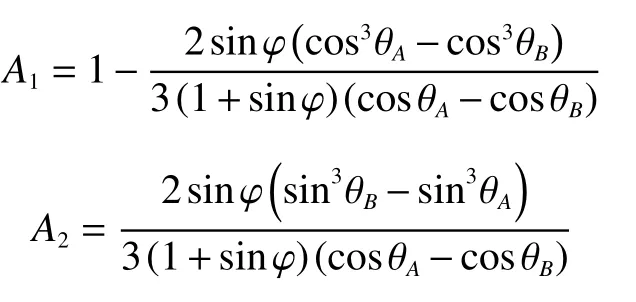
将式（4）分别代入式（8）和式（9）得：

式中：

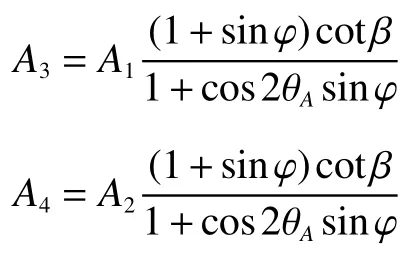
假设 Δh表示高度方向上的微小增量。同理，对CD面上的土体进行上述应力状态分析，可得墙背处C点和滑裂面处D点的小主应力迹线圆心角 θC和 θD分别为：

C点处土体竖直方向上作用的水平正应力，即高度h+Δh处的土压力强度σw(h+Δh)为：

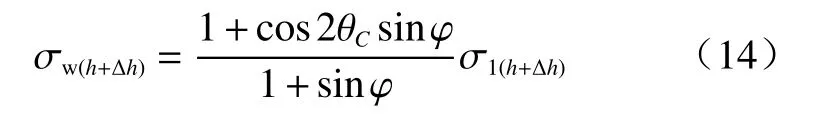
小主应力迹线C'D'的半径r(h+Δh)为：

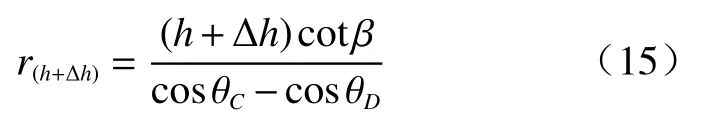
CD面上某点水平方向上作用的竖向正应力σv(h+Δh)和水平剪切应力τh(h+Δh)分别为：

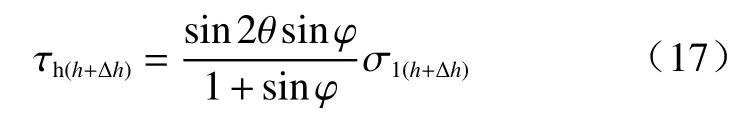
CD面上所有土体竖向正应力的合力Fσ(h+Δh)和水平剪切应力的合力Fτ(h+Δh)分别为：

3 楔体单元受力分析及主动土压力计算

3.1 楔体单元受力分析

如图3 所示，在墙后滑裂楔体内部，在距墙底h处取局部楔体OAB进行受力分析。

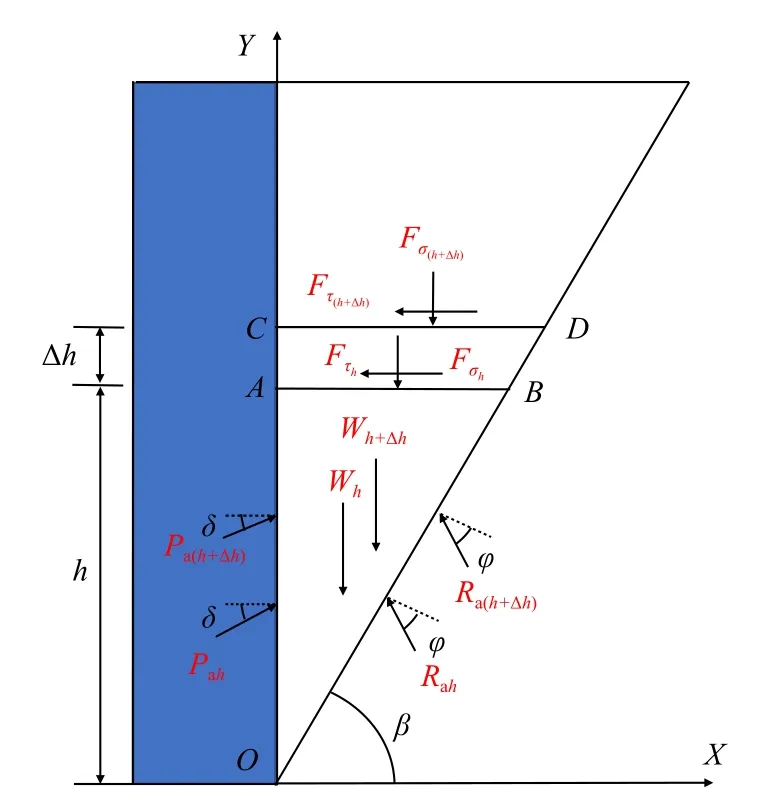
图3 楔体单元计算模型Fig.3 Wedge element calculation model

根据水平和竖直方向上的静力平衡条件可得：

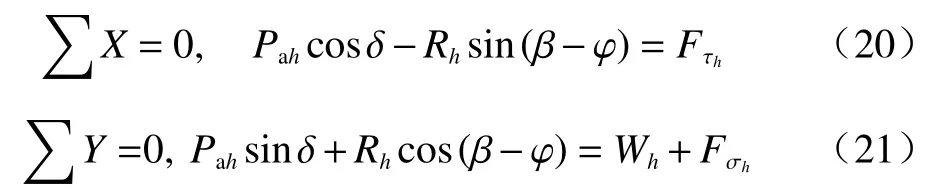
式中：Pah—挡土墙对局部楔体OAB的反力，为未知量，与局部楔体OAB产生的土压力等值反向；

Rh—滑动面上作用的反力，为未知量；

Wh—局部楔体OAB的自重。

联立式（20）（21）进行化简，可得：

式中：

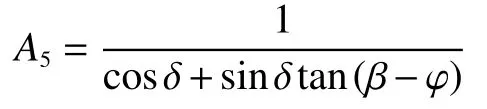
同理，对局部楔体OCD进行上述静力平衡分析，可得：

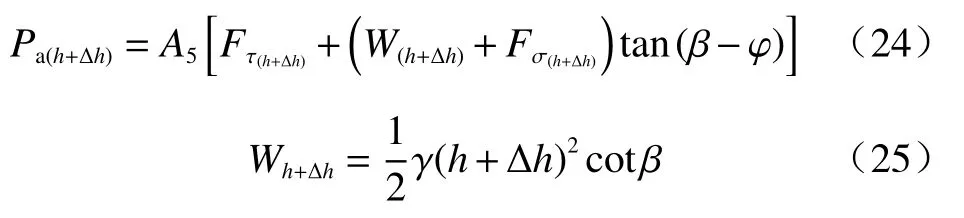
式中：Pa(h+Δh)—挡土墙对局部楔体OCD的反力，为未知量，与局部楔体OCD产生的土压力等值反向；

Wh+Δh—局部楔体OCD的自重。

3.2 主动土压力计算

由于土压力分布与土压力合力之间在数学上存在微积分的联系，根据微积分的定义[19]，当Δh→0时，有：

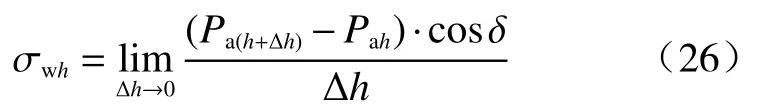
同时将σw(h+Δh)用微分增量式[19]的形式表达，即：

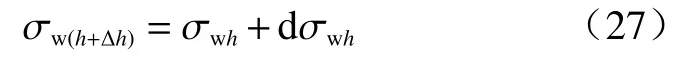
式中：dσwh—土压力强度沿墙高在 Δh高度范围内的微小增量。

将式（10）（11）（18）（19）（22）（25）（27）代入式（26）得：

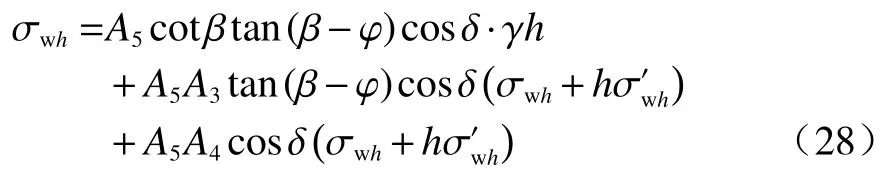
对式（28）进行化简，可得关于σwh的微分方程：

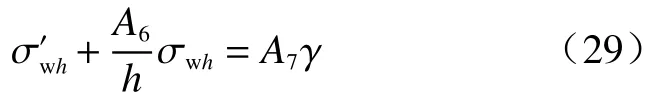
式中：

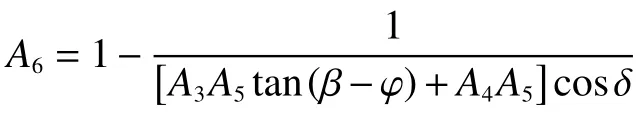
代入边界条件：当h=H时，σwh=0。求解方程（29）得：

式中：

沿墙高对土压力强度进行积分得到土压力合力，即：

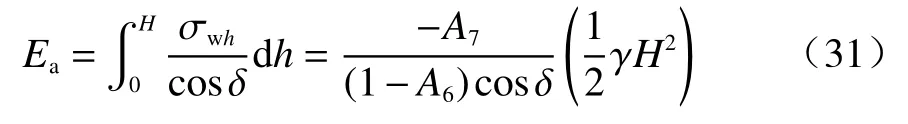
由式（31）知土压力系数Ka为：

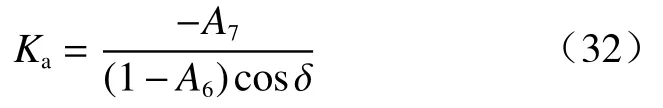
土压力合力作用点距墙底高度h0为：

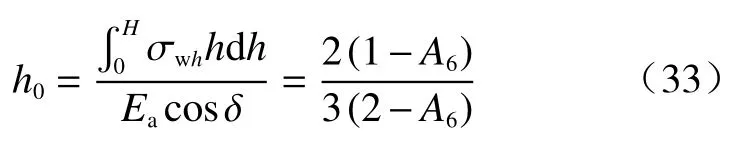
4 实例验证与参数分析

4.1 实例验证

前苏联学者Tsagareli[1]在格鲁吉亚列宁工学院进行了平动模式下刚性挡土墙的主动土压力试验。该试验的条件为：墙背垂直、墙高H=4 m；墙后填土为砂土，土体重度 γ=18 kN/m3，内摩擦角 φ=32°，墙土接触摩擦角δ=25°。为验证本文方法的合理性，分别采用本文方法、库伦方法、Paik 方法[8]、应宏伟方法[9]计算主动土压力强度，并与模型试验结果作比较，对比结果如图4 所示。由图4 可以看出，本文计算得到的土压力呈非线性分布，在挡土墙上部位置计算结果大于库伦计算结果，在挡土墙下部位置计算结果小于库伦计算结果，在靠近墙底的位置，土压力强度变化规律由增大变为减小，本文在靠近挡土墙上部位置土压力强度小于应宏伟等[9]计算结果，而在挡土墙下部位置土压力强度大于应宏伟等[9]计算结果，这主要是因为其在分析计算中忽视了计算单元界面上的水平剪切应力；本文在挡土墙墙高范围内土压力强度计算结果均小于Paik 等[8]计算结果。从数据对比分析来看，本文方法计算结果与实测数据更加接近，验证了本文方法的可行性与合理性。

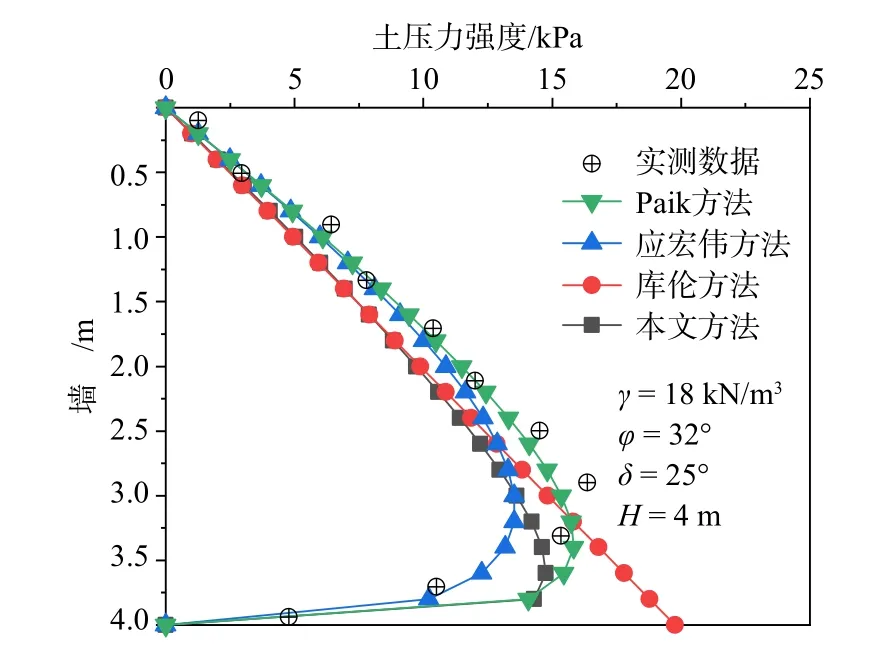
图4 本文计算结果与其他方法及Tsagareli 试验结果对比Fig.4 Comparison of the theoretical calculation results with those of other methods and Tsagareli test results

4.2 参数分析

为了更好地探讨墙土接触摩擦角 δ和填土内摩擦角 φ对土压力非线性分布的影响，以前文模型试验中的参数为基准，通过控制变量法，进行参数敏感性分析。

图5 表示墙土接触摩擦角对δ对土压力分布的影响。当 φ一定时，随着δ的增大，土压力分布曲线的拐点上移，当δ较小时，土压力近似呈线性分布。图6 表示内摩擦角 φ对土压力分布的影响，当δ一定时，随着φ的增大，土压力分布曲线的拐点下移，同一深度处的土压力强度逐渐减小。以上变化规律与Paik 等[8]和应宏伟等[9]分析结果一致。

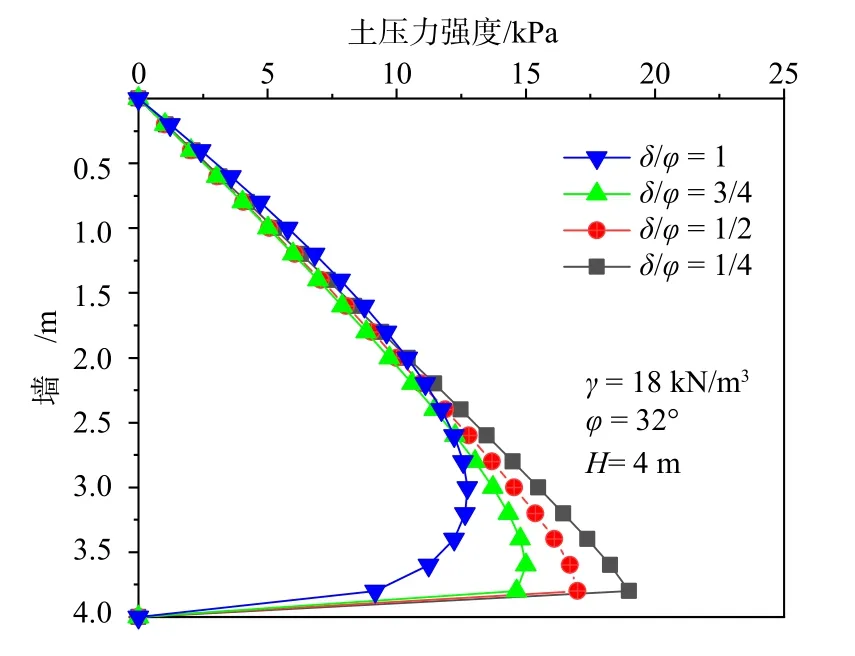
图5 墙土接触摩擦角δ 对土压力分布的影响Fig.5 Effect of the wall-soil contact friction angle δ on earth pressure distribution

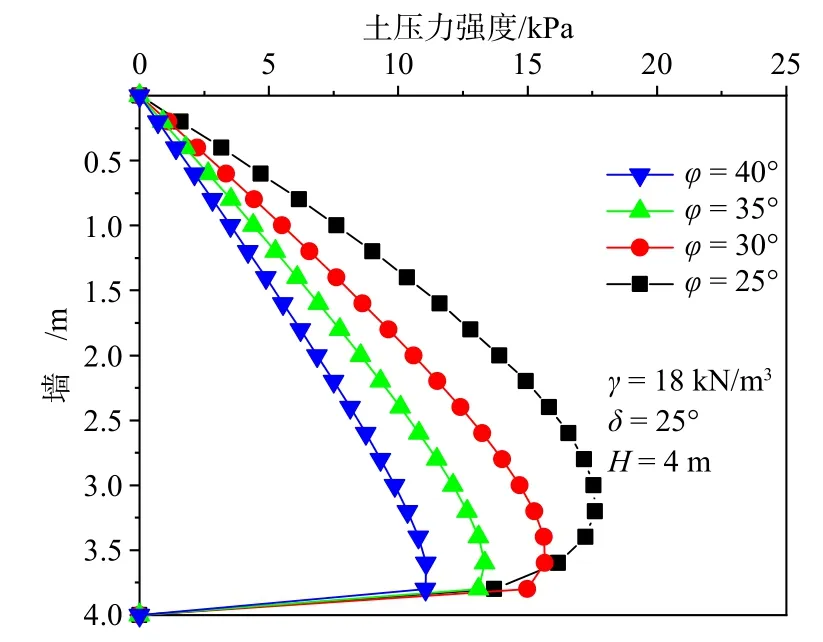
图6 内摩擦角φ 对土压力分布的影响Fig.6 Influence of the internal friction angle φ on earth pressure distribution

5 界面应力对土压力计算结果的影响分析

界面应力作为计算单元界面上作用的荷载对土压力计算结果有着重要的影响。现有研究中关于这方面的讨论甚少。本文方法力学概念清晰，便于分析界面应力的作用效果，现根据本文的计算思路，定性分析界面应力对土压力计算结果的影响。在前文的分析计算中，根据式（10）和式（11）可知，竖向正应力和水平剪切应力对计算结果的影响，实际上由A3和A4表征。因此，在讨论竖向正应力和水平剪切应力对土压力计算结果的影响时，取以下4 种情况进行分析：（1）同时考虑竖向正应力和水平剪切应力（情况一）；（2）仅考虑竖向正应力，忽略水平剪切应力，即对上述计算分析过程中取A4=0（情况二）；（3）仅考虑水平剪切应力，忽略竖向正应力，即对上述计算分析过程中取A3=0（情况三）；（4）既不考虑竖向正应力也不考虑水平剪切应力，即对上述计算过程中取A3=0、A4=0（情况四）。

对上述4 种情况通过算例分别求解土压力合力、土压力分布和土压力合力作用点。通过对计算结果进行对比，得到不均匀分布的竖向正应力和水平剪应力对土压力计算结果的影响。

5.1 界面应力对土压力合力的影响

由前文的计算分析可知，土压力系数的表达式如式（32）所示。将A6、A7的表达式代入式（32）进行化简，得：

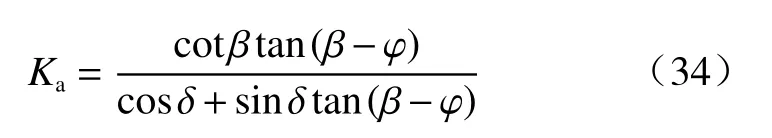
经过化简得到的土压力系数与库伦土压力系数完全一致，A3、A4作为中间变量在化简的过程中被略去。因此，实际上土压力系数与A3、A4无关，也就是说与竖向正应力和水平剪切应力无关，并且始终等于库伦土压力计算值。这表明，在分层计算的思想下，作为土体内力的竖向正应力和水平剪切应力对土压力合力的计算结果不产生影响。土压力合力大小主要取决于计算区域以及边界条件。

5.2 界面应力对土压力分布的影响

算例条件如下：墙背垂直、墙高H=1 m；墙后填土为砂土，土体重度 γ=18 kN/m3，内摩擦角 φ=36°，墙土接触摩擦角δ=12°、24°、36°，计算结果如图7 所示。计算结果表明：竖向正应力和水平剪切应力都会导致土压力呈非线性分布。仅考虑竖向正应力时（情况二），土压力分布曲线的拐点始终位于挡土墙下方，随着δ/φ值的增大而逐渐上移至挡土墙墙高中点位置附近。仅考虑水平剪切应力时（情况三），土压力分布曲线的拐点始终位于挡土墙上方，且随着δ/φ值的增大而逐渐下移至挡土墙墙高中点位置附近。当同时考虑竖向正应力和水平剪切应力时（情况一），土压力分布曲线的拐点低于上述两种情况，且随着δ/φ值的增大而逐渐上移。特别地，如果既不考虑竖向正应力也不考虑水平剪切应力（情况四），土压力分布曲线为直线，并且与库伦土压力线性分布完全一致。这点也可以根据式（28）进行分析可知，当A3=0 且A4=0 时，式（28）退化为：

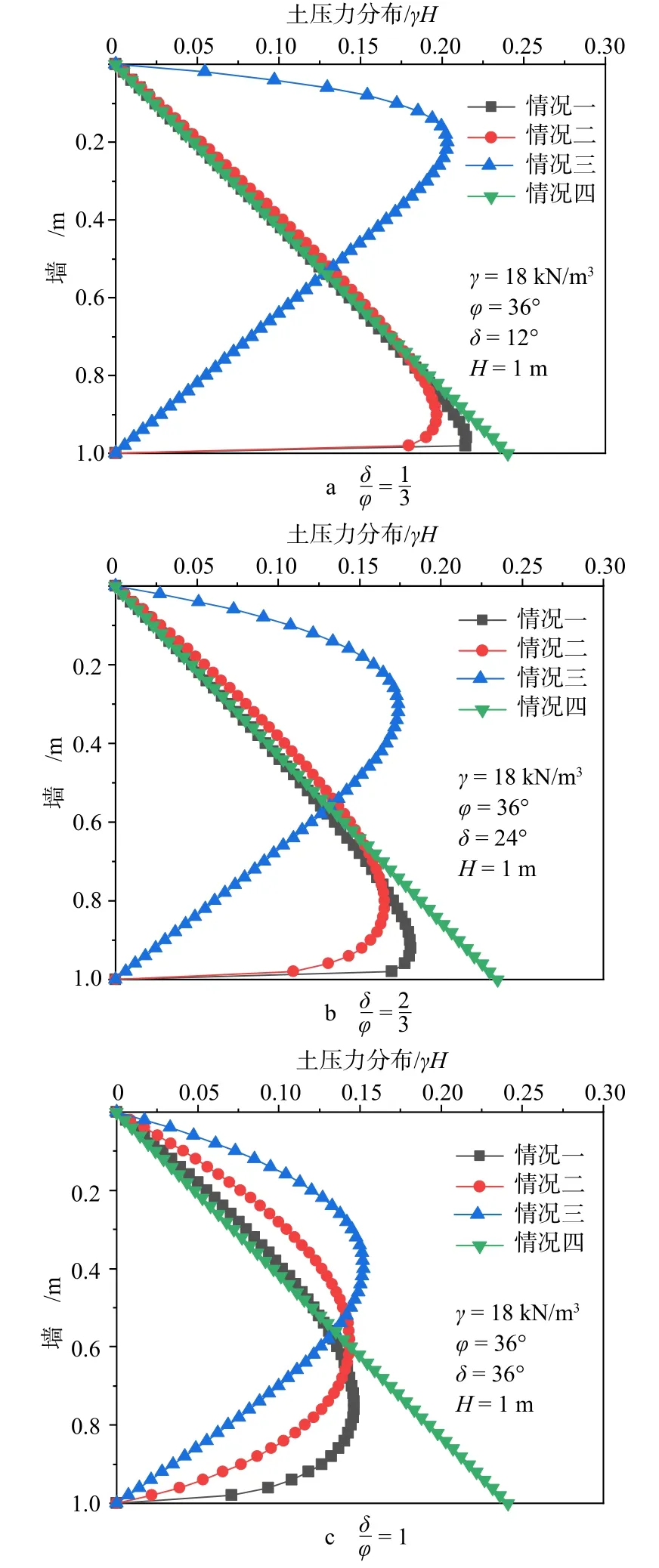
图7 不同δ/φ 值下4 种情况的土压力分布Fig.7 Earth pressure distribution in four cases with different δ/φ values

将A5的表达式代入式（35），发现此时土压力分布与库伦土压力分布完全一致。这表明，实际上库伦土压力线性分布假设的含义是计算单元界面上无应力存在。由于界面应力是土体强度发挥的表现，当界面上无应力时，也就是说，此时楔体内部的土体强度完全没有发挥。显然，这种理想情况并不会存在，因此基于库伦理论假设得到的土压力分布和合力作用点并不准确。这与工程实践得到的结论一致。

5.3 界面应力对土压力合力作用点的影响

算例条件如下：墙背垂直、墙高H=1 m；墙后填土为砂土，土体重度 γ=18 kN/m3，内摩擦角 φ=36°，墙土接触摩擦角δ=0°～36°。计算不同情况下土压力合力作用点位置h0，计算结果如图8 所示。计算结果表明：单独考虑竖向正应力或水平剪切应力作用时，土压力合力作用点位置都会得到提高。在填土内摩擦角 φ一定的情况下，如果仅考虑水平剪切应力的作用，当墙土接触摩擦角δ=0°时，土压力合力作用点位置起始于距墙底2H/3 处，且随着墙土接触摩擦角δ的增大而逐渐减小至距墙底0.55H左右处，土压力合力作用点位置始终高于0.50H，位于挡土墙上部位置。其他三种情况下，土压力合力均起始于距墙底H/3 处，其中仅考虑竖向正应力和同时考虑竖向正应力和水平剪切应力两种情况下，土压力合力作用点位置随墙土接触摩擦角δ的增大而逐渐增大，土压力合力作用点位置始终低于0.50H，位于挡土墙下部位置。但在仅考虑竖向正应力作用的情况下，土压力合力作用点位置高于同时考虑竖向正应力和水平剪切应力的情况。由于在同时考虑竖向正应力和水平剪切应力的情况下，土压力合力作用点的规律更加接近于仅考虑竖向正应力的情况，这说明实际上相对于水平剪切应力而言，竖向正应力对土压力分布以及土压力合力作用点的影响更大。特别地，如果既不考虑竖向正应力也不考虑水平剪切应力作用时，由于此时土压力分布和库伦线性土压力完全一致，因此土压力合力作用点与库伦土压力作用点完全一致，始终位于距墙底H/3 处。

图8 不同情况下土压力合力作用点规律Fig.8 Law of the action point of the resultant earth pressure in different situations

6 结论

（1）考虑分层界面上应力分布不均匀，可以更准确地描述土压力的分布规律。土压力分布曲线的拐点随着墙土接触摩擦角δ的增大而上升，随着填土内摩擦角 φ的增大而下降。土压力合力作用点位置随着δ/φ的增大而上升。

（2）界面应力作为滑动楔体内部土体的内力不会对土压力合力的大小产生影响，但会对土压力分布和土压力合力作用点位置产生影响。在仅考虑竖向正应力的情况下，土压力分布曲线为下部凸起的鼓形，土压力合力作用点位置随δ/φ的增大而上升，并且始终位于挡土墙墙高中点以下。而在仅考虑水平剪切应力的情况下，土压力分布曲线为上部凸起的鼓形，土压力合力作用点位置随δ/φ的增大而下降，并且始终位于挡土墙墙高中点以上。在不考虑竖向正应力和水平剪切应力作用的情况下，土压力分布与库伦土压力线性分布假设完全一致。这表明库伦土压力的内涵是楔体内部土体强度完全没有发挥。

（3）对于单元界面上客观存在的竖向正应力和水平剪切应力而言，相比于水平剪切应力，竖向正应力对土压力计算结果的影响更大。