基于上下文表示的知识追踪方法*
2022-09-21王文涛马慧芳舒跃育贺相春
王文涛,马慧芳,舒跃育,贺相春
(1.西北师范大学计算机科学与工程学院,甘肃 兰州 730070;2.西北师范大学心理学院,甘肃 兰州 730070;3.西北师范大学教育技术学院,甘肃 兰州 730070)
1 引言
近年来,随着在线评测OJ(Online Judge)系统[1]和大规模在线开放课程MOOC(Massive Open Online Course)[2]等平台的日益普及,越来越多的学生能够实现在线自主学习。然而在线教育系统在带来便利的同时,其提供的海量学习资源往往使得学生在进行自主学习时面临诸多困难,例如学生如何在众多学习资源中选择最适合自身情况的资源,在线教育平台如何为学生推荐一套个性化的学习资源等。随着教育数据挖掘技术的迅猛发展,已有大量的致力于知识追踪方法的研究工作。尽管这些方法取得了一定的效果,但其大多将知识点视为一个独立的实体进行建模,并且对于利用影响学生学习过程的复杂学习因素对知识点进行上下文表示的研究还不够充分[3]。
传统知识追踪方法主要基于概率模型对学生与习题之间的交互关系进行建模,其中基于隐马尔可夫模型的贝叶斯知识追踪BKT(Bayesian Knowledge Tracing)方法[4]是最具代表性的知识追踪方法之一,该方法构建了学生认知状态的动态变化过程,以监测和估计学生掌握知识点的概率。然而,这类方法使用的交互函数高度依赖于领域专家的人工设计,且忽略了学生的认知遗忘因素,即认为学生一旦掌握某个知识点后就不再遗忘。由于人类的知识及大脑具有天然复杂性,使用复杂的网络结构来设计知识追踪方法应该更为合适,然而大多数现有方法的设计仍然是基于具有严格约束函数的一阶隐马尔可夫模型。随着深度学习技术的不断发展,一些使用神经网络技术的方法对传统知识追踪方法进行了改进,主要分为以下2类:
(1)省略专家标注知识点的过程,即不使用习题与知识点之间的关联信息而直接对学生知识状态进行估计。Piech等人[5]使用循环神经网络并结合学生历史答题序列数据对学生与习题之间的交互关系进行建模,提出了深度知识追踪DKT(Deep Knowledge Tracing)方法,在不需要专家标注习题与知识点关系的情况下,显著提升了传统BKT方法作答表现预测的性能。Zhang等人[6]在结合BKT和DKT两者优点的基础上,将记忆增强网络MANN(Memory-Augmented Neural Networks)应用于知识追踪问题,通过引入key-value存储单元,提出了动态键值记忆网络DKVMN(Dynamic Key-Value Memory Networks for knowledge tracing)模型,以发现每个输入习题的潜在知识概念,跟踪学生对知识点的认知状态。
(2)尽管第(1)类方法在性能上优于传统知识追踪方法,但是随着对学生知识状态结果的研究与分析不断深入,发现由第(1)类方法估计出的学生知识状态不具有可解释性,并且领域专家标注的习题与知识点间的关联信息不容忽视。针对这些问题提出的方法被称为第(2)类方法。Huo等人[3]认为虽然诸如DKT和DKVMN等方法能够自动识别出习题考察的潜在知识点,但却不能保证识别结果比专家人工标注的知识点更可靠,故在此基础上对知识点进行上下文化,提出了LSTMCQP(Long Short-Term Memory network using CQ-matrix and Personalization mechanism)方法。尽管该方法在对知识点的上下文表示上进行了探索,但其效果对数据集较为敏感。
针对以上方法存在的问题,本文设计了基于上下文表示的知识追踪方法KTCR(Knowledge Tracing via Contextualized Representations)。该方法既考虑了习题与知识点之间的关联信息,又综合考虑了学生在学习过程中的复杂学习背景对知识点基于上下文表示。首先,基于学生响应数据及其在知识点上的综合表现情况,设计一种对知识点基于上下文表示的方法,从而实现对知识点进行上下文信息的嵌入;其次,利用基于上下文表示后的知识点对习题进行有效表示,以实现习题向量的降维处理;最后,结合降维后的习题向量和学生历史交互数据,利用长短期记忆LSTM(Long Short-Term Memory)网络[7]对学生的知识状态进行追踪。本文将所提方法应用于4个真实数据集上,实验结果表明,本文所提方法能够有效地对习题进行嵌入表示,并且能较好地估计学生知识状态。
2 准备知识
2.1 问题定义
设有N个学生,M道习题,K个知识点,记学生集S={s1,s2,…,sN},习题集E={e1,e2,…,eM}和知识点集C={c1,c2,…,cK}。习题与知识点之间的关联信息用二元矩阵QM×K来表示,矩阵中元素qmk表示第m道习题是否包含第k个知识点(包含为1,否则为0)。此外,学生的响应数据(即历史做题数据)用矩阵RN×M表示,每一行表示学生在M道题上的交互情况(答对记为1,答错记为0,未交互记为-1)。因此,对于知识追踪而言,其任务是预测在t+1时刻第i个学生将一道题回答正确的可能性,即P(yt+1=1|Ф,Q,R,C,E,S),其中Φ为模型的参数集合。
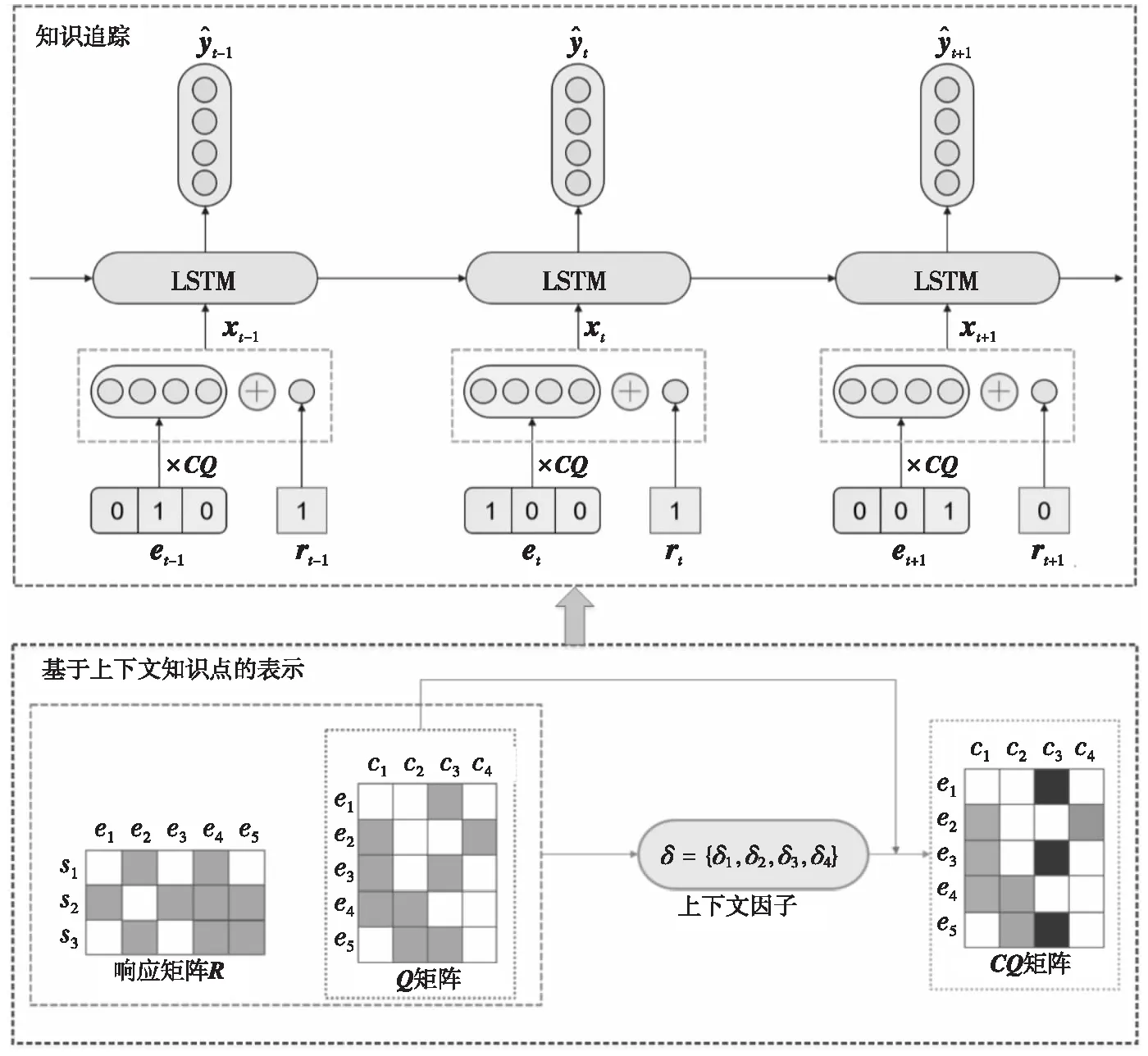
Figure 1 Framework of knowledge tracing based on contextualized representations method图1 基于上下文表示的知识追踪方法框架
2.2 Q矩阵
随着教育心理学领域的不断发展,对认知诊断评估方法的研究已经成为近年来的研究重点。基于学生在习题上的作答情况,认知诊断方法可以对学生进行个性化的认知诊断建模。具体地,认知诊断方法假设习题和知识点之间存在显示关联,可以通过Q矩阵来刻画这种相关关系,如表1[8]所示。
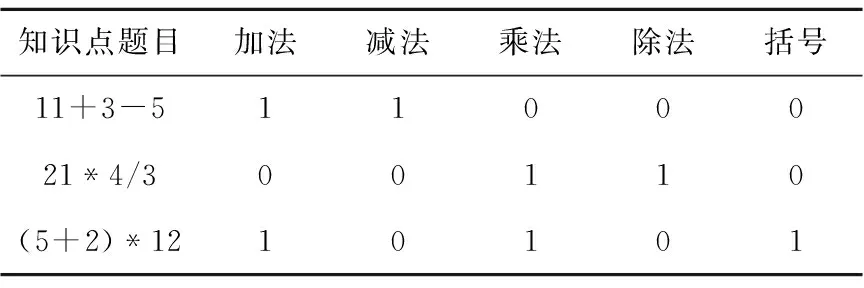
Table 1 Q matrix about the correlations between exercises and knowledge concepts
认知诊断方法将学生的知识状态分解为若干个具体知识点,并通过学生的响应数据和Q矩阵来评价学生对这些知识点的掌握程度[9]。由此可见,Q矩阵在认知诊断评估方法中有十分重要的作用,使模型能够为学生提供特定知识点上细粒度的诊断信息,具有非常重要的研究意义。然而,已有的一些知识追踪方法,例如DKT和DKVMN等方法,摒弃了习题与知识点之间的关联信息,利用模型自身得到习题的潜在知识点,然而通过此种方式得到的知识点与学生知识状态无法对应,导致最终得到的学生知识状态不具有可解释性。因此,将Q矩阵中习题和知识点之间的关联信息引入知识追踪方法中很有必要。
2.3 方法框架
本文方法的框架如图1所示:首先,通过学生响应矩阵R和习题知识点关联矩阵Q设计一种基于知识点上下文表示的计算策略,对Q矩阵进行上下文表示,得到上下文化Q矩阵CQ(Contextualized Q-matrix);其次,利用CQ矩阵和学生响应数据对习题进行嵌入表示,从而在实现习题向量降维的同时丰富了其语义信息;最后,结合基于上下文表示的习题向量和学生历史交互数据,通过LSTM对所有学生的知识状态进行估计,最终得到学生在所有知识点上的掌握状态。为了描述清晰起见,表2集中给出了本文方法中涉及到的常用符号定义。

Table 2 Definition of commonly used symbols
3 KTCR方法
3.1 基于上下文的知识点表示
不同于DKT和DKVMN直接利用学生在习题上的表现情况作为估计学生知识状态的依据,KTCR致力于综合考虑学生在习题和知识点上的表现情况,以此将学生的客观反馈与专家主观标注的知识点信息进行融合。值得注意的是,“习题表现”与“知识点表现”是2个不同的概念。例如能够正确回答考察了“相似三角形”相关习题的学生,在同时考察“相似三角形”和“勾股定理”相关的习题中却可能出错,这是由于“连接要求”[10],即学生必须掌握所有与习题相关的知识点才能正确回答该习题。因此,KTCR不仅考虑了学生在习题上的表现情况,同时还计算了学生在知识点上的表现情况。而随着学生交互的习题数量的增加,其在知识点上的表现情况会有所波动,造成这种波动的原因可能是学生的复杂学习背景,例如习题难度、教学相关的因素以及习题与其他知识点的关联等。然而,由于对这些复杂学习背景的建模十分困难,本文并非试图去识别和建模每一个学习背景,而是将其视为一个复合结果,即上下文。
为此,本节通过学生响应矩阵和习题知识点关联矩阵Q设计一种知识点上下文计算策略,以此实现Q矩阵的上下文表示,得到上下文化后的Q矩阵,即CQ矩阵。具体地,首先考虑所有学生交互过的习题数量,用集合e(s)表示,即e(s)={e(s1),e(s2),…,e(sN)};其次考虑所有学生与考察了第l个知识点的习题的交互数量,用集合el(s)表示,即el(s)={el(s1),el(s2),…,el(sN)},故第i个学生在考察了第l个知识点的习题中,其答题正确率accl(si)如式(1)所示:
(1)
其中,I(·)为指示函数,当满足条件“·”时函数值为1,否则为0。故第l个知识点的上下文因子如式(2)所示:
(2)
其中,σ[·]为sigmoid函数。接着由Q矩阵和知识点上下文因子可得CQ矩阵,如式(3)所示:
CQ[:,l]=δl×Q[:,l]
(3)
其中,列向量CQ[:,l]为CQ矩阵中的第l列,列向量Q[:,l]为Q矩阵中的第l列。
因此,借助于知识点上下文因子,实现了从Q矩阵到CQ矩阵的上下文表示转换。接下来,给出一种习题嵌入表示方法,将学生习题表现与知识点表现进行融合,从而得到习题的向量表示。
3.2 习题向量表示
在DKT中,习题向量的维度为习题数量的2倍,且由one-hot向量进行表示。这样的习题向量不仅携带的语义信息十分有限,而且习题向量高维稀疏,都将影响模型的最终性能。为此,本节利用CQ矩阵与学生响应数据来得到每道习题的嵌入表示。
对于t时刻与第i个学生交互的习题初始嵌入向量表示如式(4)所示:
(4)
其中,et为该题的one-hot表示。
有别于DKT中通过隐含方式表示学生响应数据,此处直接引入响应数据。即对于第i个学生而言,其在t时刻传递到LSTM中的输入向量如式(5)所示:
xt=[cqt,rt]T
(5)
其中,cqt为t时刻与第i个学生交互过的习题初始嵌入向量,rt为对应的响应数据。因此,通过使用CQ矩阵与响应数据对习题向量进行重表示,使得习题嵌入向量在DKT的基础上实现降维的同时,还包含了习题知识点关联的细粒度语义信息。
3.3 知识追踪
在得到习题向量表示之后,将其作为LSTM的输入,从而估计学生在知识点集合上的掌握情况,如式(6)~式(12)所示:
it=σ(Wixt+Uiht-1+bi)
(6)
ft=σ(Wfxt+Ufht-1+bf)
(7)
ot=σ(Woxt+Uoht-1+bo)
(8)
(9)
(10)
ht=ot∘tanh(zt-1)
(11)
(12)

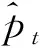
(13)
在明确模型的输入输出之后,则需要建立模型的损失函数。对于单个学生的损失函数建模如式(14)所示:
(14)
算法1KTCR方法
输入:响应矩阵R,习题知识点关联矩阵Q,学生集S={s1,s2,…,sN},习题集E={e1,e2,…,eM}和知识点集C={c1,c2,…,cK}。
输出:t+1时刻第i个学生在第j+1个习题上回答正确的概率,即P(yt+1=1 | Ф,R,Q,S,E,C) 。
步骤1计算所有学生交互过的习题数量,得e(s)={e(s1),e(s2),…,e(sN)};
步骤2计算所有学生与考察了第l个知识点的习题的交互数量,得el(s)={el(s1),el(s2),…,el(sN)};
步骤3初始化长度为N的一维全零数组ACC;
步骤4 forl=1 toKdo
步骤5fori=1 toNdo
步骤6利用式(1)计算第i个学生在考察了第l个知识点的习题中的答题正确率accl(si);
步骤7ACC[i]=accl(si);
步骤8endfor
步骤9利用数组ACC与式(2)计算第l个知识点的上下文因子δl;
步骤10利用式(3)对Q矩阵的第l列进行上下文表示;
步骤11 endfor
步骤12 fori=1 toNdo
步骤13forj=1 toMdo
步骤14ifrij=1 orrij=0
步骤15利用式(4)和式(5)得当前习题向量x;
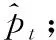
步骤18endif
步骤19endfor
步骤20根据式(14)计算第i个学生的损失函数L;
步骤21while第i个学生的损失函数未收敛do
步骤22利用SGD算法更新参数集合Ф;
步骤23执行步骤12~步骤20;
步骤24endwhile
步骤25 endfor
4 实验与结果分析
为了验证本文方法的合理性与有效性,本文设计实验进行验证。实验将回答以下几个问题:
(1)KTCR方法与现有的一些知识追踪方法相比,性能方面存在哪些优势?
(2)使用KTCR方法得到学生知识状态估计结果的准确性如何?
(3)在真实数据集上,KTCR方法对估计学生知识状态的贡献如何?
在本节中,首先介绍实验所使用的数据集;其次介绍实验设置与基线方法;再次根据所提问题对评价指标进行介绍;最后对实验结果进行分析,并结合案例分析阐释本文方法的合理性与有效性。
4.1 实验数据集描述
实验所用的4个公开数据集分别为:ASSISTment2009(ASSIST2009)、ASSISTment 2015(ASSIST2015)、ASSISTment Challenge(ASSISTChall)和STATICS,其中每个数据集的相关信息如下所示:
(1)ASSIST2009数据集是2009年由ASSISTment在线教育平台所收集的,是知识追踪相关论文中使用最广泛的数据集之一[11]。由于原始数据集中有大量重复的交互记录存在,故在数据预处理时删除了重复部分,最终得到的数据集包含4 417名学生的328 291条做题记录,其中与学生交互的习题来自于124个不同的知识点。
(2)ASSIST2015数据集与ASSIST2009类似,同样来源于ASSISTment在线教育平台。不同的是,该数据集是由平台在2015年收集的,包含19 917名学生的708 631条做题记录,其中知识点个数为100个。
(3)ASSISTChall数据集来自于2017年ASSISTment平台的数据挖掘竞赛,该数据集包含686名学生的942 816条交互记录和102个知识点。
(4)STATICS数据集是从大学的工程力学课程中收集的[6],包括333名学生在来自于1 223个知识点的习题上的189 927条做题记录。
表3总结了上述4个数据集的统计信息。
4.2 实验设置与对比方法
4.2.1 实验设置
实验将4个数据集分别划分为训练集和测试集,抽取其中20%的学生做题记录作为测试集,剩余部分为训练集。为了保证实验结果的可靠性,实验采用5次5折交叉验证法评价KTCR方法的性能。
在KTCR方法的训练阶段,隐含层使用了150个LSTM单元,keep_prob设为0.5,学习率learning_rate设为0.01,训练轮数max_epoch为200,每批数据的大小batch_size设为32。实验使用Xavier[12]中的初始化参数,其对权重初始化的随机值采样于N~(0,std2)。此外,实验所用操作系统为Windows10 64位,显卡为NVIDIA GTX1080-8 GG,内存为16 GB,实验代码通过Python3.6.5由TensorFlow1.10实现。
4.2.2 基线方法
为评估KTCR方法的性能,选取以下2类方法作为基线方法:(1)只考虑学生响应数据,不考虑习题与知识点之间的关联信息,即DKT和DKVMN;(2)融合了习题与知识点之间的关联信息,即 LSTMCQ及KTCR的几种变体方法。具体描述如下:
(1)DKT[5]:实验采用DKT的LSTM实现方法,使用one-hot向量来表示一道习题,向量维度为2×106。当t时刻模型的输入向量为xt=[et,0]T时,表示该题在真实情况下学生回答正确,即rt=1,其中,0表示与et维数相同的全0向量;而当t时刻模型的输入向量为xt=[0,et]T时,则表示该题在真实情况下学生回答错误。
(2)DKVMN[6]:该方法在记忆增强网络MANNs(Memory-Augmented Neural Networks)[13,14]的基础上,结合了BKT和DKT的优点,对学生知识状态进行追踪。
(3)LSTMCQ[3]:该方法在DKT的基础上使用文献[3]中的基于上下文表示方法对Q矩阵进行重表示。
(4)Q-DKT:该方法为KTCR方法的一种变体方法。Q-DKT将习题嵌入向量中习题正确与否的信息用类似DKT中的方法进行表示,并且未使用3.1节中的知识点上下文表示对Q矩阵进行上下文化。在3.2节中提到的KTCR方法在t时刻传递到LSTM中的输入向量为xt=[cqt,rt]T,而对于Q-DKT,t时刻传递到LSTM中的输入向量为xt=[qt,0]T或xt=[0,qt]T,其中0的含义与DKT中的类似,其维度与qt相同。
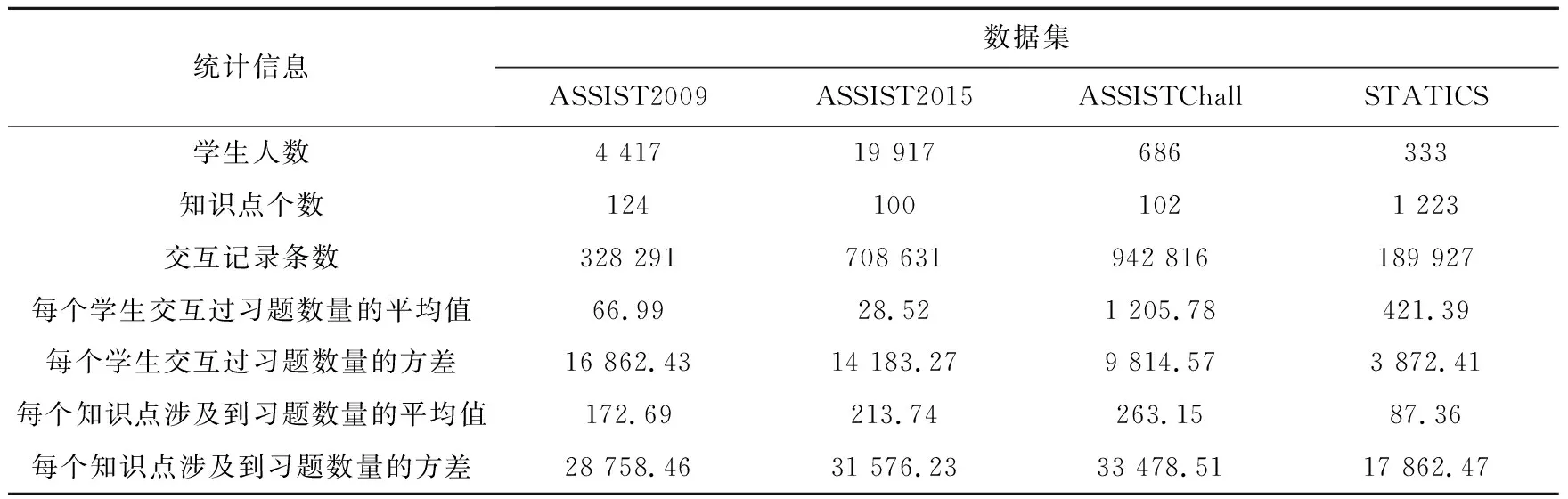
Table 3 Statistics of all datasets
(5)QR-DKT:该方法为KTCR方法的一种变体方法。QR-DKT在Q-DKT的基础上将学生响应数据显式表示,使用未经上下文化的Q矩阵对习题向量进行降维。即t时刻传递到LSTM中的输入向量为xt=[qt,rt]T。
4.3 评价指标
4.3.1 学生答题情况预测
由于无法得到真实情况下学生在知识点上的掌握情况,故对知识追踪方法进行性能评估是很难做到的。之前的很多工作大都是通过预测学生的做题情况来得到追踪结果,通过在此类预测任务上模型的表现,可以间接地从某个层面对知识追踪方法进行评估。考虑到实验数据中使用的所有习题都是客观题,实验从分类和回归2个角度使用评价指标来评估模型预测的学生答题情况,包括准确率Accuracy[15]、均方根误差RMSE[16]和AUC(Area Under ROC),其定义如下所示:
定义1准确率(Accuracy):基于混淆矩阵(如表4所示),Accuracy是分类正确的样本数量占样本总数的比例,如式(15)所示:
(15)

Table 4 Confusion matrix
定义2均方根误差(RMSE):基于学生响应数据与模型预测结果,RMSE的定义如式(16)所示:
(16)

此外,实验还将选用受试者工作特征ROC(Receiver Operating Characteristic)曲线下的面积AUC作为方法性能评价指标之一。选用AUC作为本文方法评价指标的原因有二:(1)AUC作为性能度量指标在机器学习领域凭借其优越性得到了广泛应用;(2)在知识追踪任务中,相关论文均使用AUC作为性能度量指标,因此本文选用AUC来评价性能,易于同其他知识追踪方法进行比较。
4.3.2 学生知识状态估计
除了从预测学生答题情况的层面来评价本文方法外,还引入DOA(Degree of Agreement)[15]作为预测的准确性指标。
定义3一致性(DOA):DOA用来比较方法预测的学生知识状态与学生真实答题情况之间的一致程度,其定义如式(17)所示:
(17)
其中,KSak为第a个学生在第k个知识点上的掌握情况,I(·)为指示函数,qjk为Q矩阵中的第j行第k列中的元素,raj表示第a个学生的真实做题情况。从直觉上来说,如果第a个学生比第b个学生在第k个知识点上的掌握情况更好,那么第a个学生就更有可能比第b个学生答对与第k个知识点相关联的那些习题。DOA值越高,表明模型预测的学生知识状态与实际结果越一致,即预测的学生知识状态更准确。
4.4 实验结果与分析
4.4.1 性能比较
表5显示了在不同数据集上本文KTCR方法与各基线方法的准确率、均方根误差及AUC值。表5中的数值为经过5次5折交叉验证后各方法在4个数据集上的各指标数据平均值。从表5中可以看出:首先,使用Q矩阵作为习题嵌入信息的方法性能基本上优于未使用Q矩阵的方法。这是由于Q矩阵为模型提供了习题与知识点之间的细粒度关联信息,从而在一定程度上提升了方法的性能。其次,在使用Q矩阵的方法中,2种使用不同知识点上下文策略的方法(即本文方法与LSTMCQ方法)性能始终优于另2种方法,这说明对知识点进行基于上下文表示能够使习题向量携带更加丰富的语义信息,使得模型性能有所提高。具体对于LSTMCQ方法而言,由于其对知识点上下文表示的局限性,导致其在数据集ASSIST2009和数据集ASSIST2015上的表现与未使用Q矩阵的2种方法差别不大,即LSTMCQ方法对数据集敏感。相反,由于本文在设计知识点上下文表示策略时,既考虑了在某一知识点上的学生交互人数,又将每个学生交互过的习题数量作为可信度考虑在内,因此KTCR方法在保证了方法有效性的同时,还在不同数据集上具备性能的稳定性。
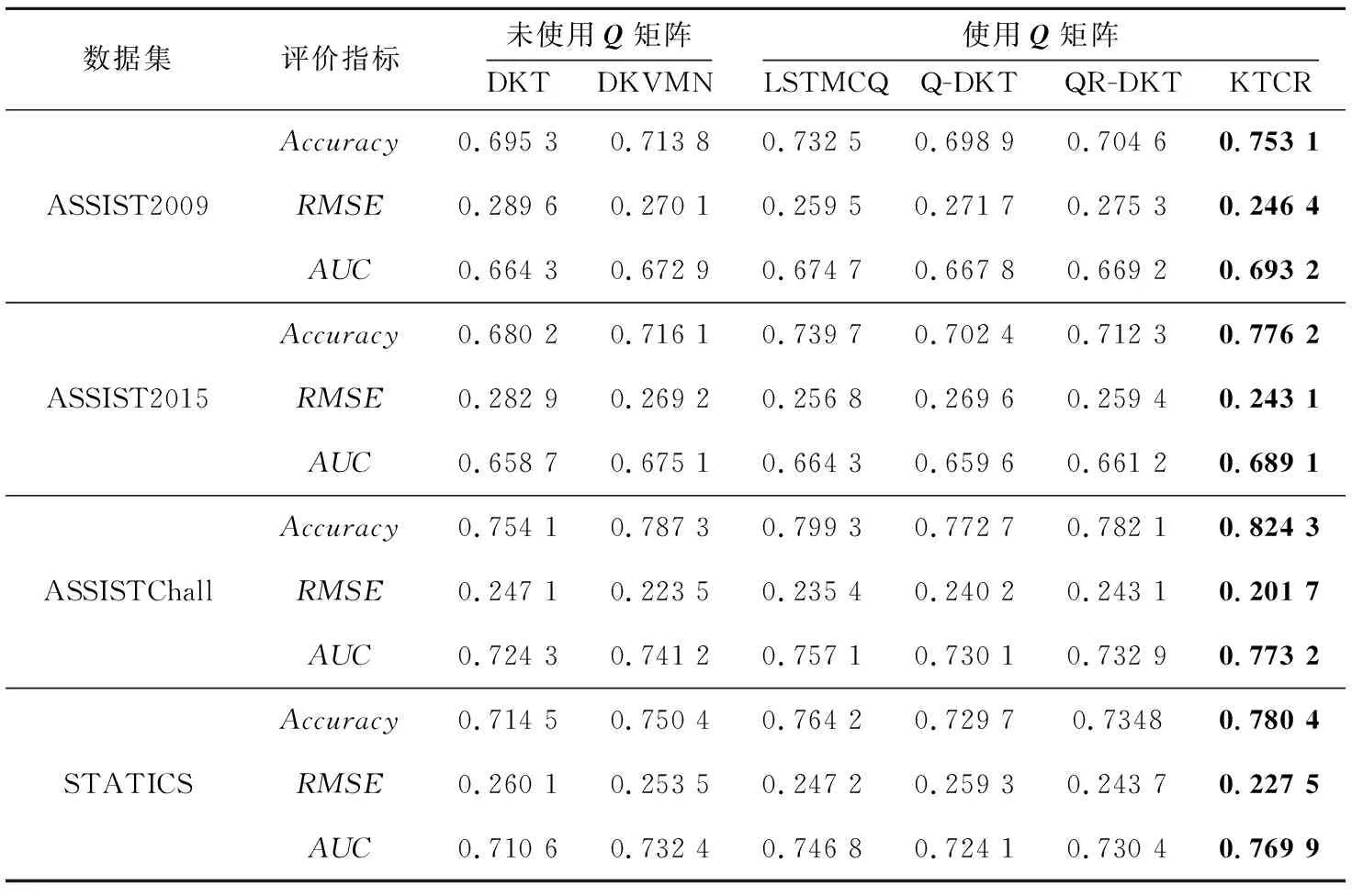
Table 5 Experimental results of student performance prediction
4.4.2 学生知识状态准确性研究
为了评价KTCR方法获取学生知识状态的准确性,本文在所有知识点上对DOA取平均值,结果如图2所示。
Figure 2 DOA results of different methods on four datasets图2 4个数据集上不同方法的DOA值
由于未使用Q矩阵的DKT方法和DKVMN方法得到的学生知识状态无法与真实数据集中的知识点相匹配,因此实验仅将KTCR方法与本文变体方法及LSTMCQ方法从一致性角度进行比较。由图2可知,KTCR方法的DOA显著高于其他基线方法的,说明使用KTCR方法得到的学生知识状态相较于基线方法更准确,与真实情况更一致。与此同时,观察到KTCR和LSTMCQ方法的DOA普遍高于Q-DKT和QR-DKT方法的,这同样说明了知识点的基于上下文表示对获得准确的学生知识状态具有重要作用。
4.5 案例分析
本节通过设计一个案例来分析KTCR方法对估计学生知识状态的贡献。图3给出了基于ASSIST2009数据集的KTCR方法在学生与习题交互序列中捕获编号为80807的学生知识状态的过程案例。由图3中的案例可知,学生在连续回答了5道来自5个不同知识点的习题之后,经过KTCR方法对学生答题序列中学生知识状态的挖掘,最终获取学生在5个知识点上的掌握情况。从图3中左侧的雷达图中观察到该学生在“相似三角形”和“勾股定理”2个知识点上掌握得较好,而对于其余知识点则掌握得较差,此结果与学生答题序列反映出来的信息基本一致。
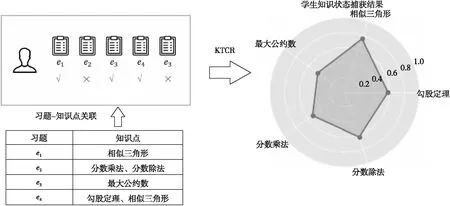
Figure 3 Process of capturing a student’s knowledge state by KTCR图3 KTCR捕获编号为80807的学生知识状态的整体过程
5 结束语
本文针对现有方法未能充分利用习题与知识点之间关联信息的局限性,提出了基于上下文表示的知识追踪方法KTCR。该方法既考虑了习题与知识点之间的关联信息,又综合考虑了学生在学习过程中的复杂学习背景对知识点基于上下文表示。在真实数据集上的大量实验验证了本文KTCR方法的有效性与知识状态追踪结果的可解释性。
