基于转换域与自适应伽马校正的去雾算法*

王 蓉,杨 燕

(兰州交通大学电子与信息工程学院，甘肃 兰州 730070)

1 引言

雾、霾等恶劣天气条件下，由于空气中悬浮的气溶胶、水滴等颗粒会对光线产生散射，导致捕获的室外图像出现对比度降低、颜色失真和细节模糊等降质问题[1]，对户外物体识别、障碍物检测、视频监控和智能运输等计算机视觉系统造成极大影响。因此，对降质图像进行有效的清晰化处理具有重要的研究意义和实际应用价值。

目前，图像去雾算法主要分为3大类：基于图像增强的算法、基于图像复原的算法和基于机器学习的算法。基于图像增强的算法并未考虑图像退化的本质原因，仅通过提高对比度、突出场景特征对降质图像作简单的清晰化处理，极易造成图像过度增强且丢失局部细节，从而不能实现真正意义上的去雾。经典的基于图像增强的算法包括小波变换[2]、直方图均衡化[3]和Retinex算法[4]等。

基于机器学习的算法通过构建网络模型并对其进行训练，进而得到复原的无雾图像。Cai等人[5]提出了一种基于端到端的卷积神经网络架构，通过学习有雾图像与其对应透射率图之间的映射关系来实现场景复原。Ren等人[6]提出了一种多尺度卷积神经网络去雾算法，首先使用粗尺度网络对场景透射率进行粗略估计，再通过另一个细尺度网络进一步优化得到复原图像。Li等人[7]根据重构的大气散射模型提出一种一体化去雾网络AOD-Net(All-in-One Dehazing Netwok)，该网络与大多数分别估计透射率和大气光的模型不同，可通过轻量级卷积神经网络直接生成无雾图像。Qin等人[8]提出了一种端到端的特征融合注意力网络FFA-Net(Feature Fusion Attention Network)，可以有效提取图像特征并直接恢复无雾图像，但对于真实场景有雾图像复原效果并不理想。尽管深度学习是目前各个领域的研究热点，但对于图像去雾而言，由于缺乏大量的真实图像数据集对网络进行训练，导致该类方法在真实场景雾图处理方面效果欠佳，因而在实际应用中具有一定的局限性。

基于图像复原的算法通过分析图像退化机理建立物理模型，利用特定的先验或假设估计模型中的未知参数，实现自然场景的有效复原。Tan[9]基于大量统计信息发现无雾图像对比度远高于有雾图像，进而采取最大化局部对比度来达到去雾的目的，得到的复原图像具有较好的视觉效果，但容易出现过饱和及光晕效应。Fattal[10]假设物体表面阴影与介质传输率局部不相关，通过独立成分分析法实现场景复原，但由于缺乏足够的颜色信息,对于浓雾图像及灰度图像该算法无效。He等人[11]通过观察大量无雾图像统计特性，提出了暗通道先验理论，并结合大气散射模型复原出清晰无雾的图像，但该算法不适用于含有天空等明亮区域的图像，且复原结果在景深突变处易出现光晕及块状伪影。Meng等人[12]提出了一种基于边界约束的正则化去雾算法，以牺牲部分细节为代价来获得较好的复原结果。Zhu等人[13]提出了一种线性颜色衰减先验理论，对雾图景深(指有雾图像的场景深度)进行建模并使用监督方法学习模型参数，能恢复较多的细节信息但去雾不够彻底。

针对上述图像复原算法的不足，本文提出了一种改进算法，在避免暗通道先验算法景深突变处易产生光晕伪影及天空等明亮区域偏色现象的同时，保持复原结果去雾彻底且清晰自然。首先，对大气散射模型作对数变换，结合暗通道先验理论提出对数域正相关关系；然后建立高斯函数进行拟合得到粗级透射率，再利用自适应伽马校正技术与交叉双边滤波操作对透射率进行优化；最后，设定不同尺寸的滤波核执行闭操作，以获得改进后的局部大气光，结合大气散射模型实现无雾图像的有效复原。实验结果表明，本文算法去雾效果较好，能有效地恢复出图像的细节信息。

2 背景

2.1 大气散射模型

在计算机视觉和图像处理领域中，通常以大气散射模型[14,15]为理论基础对雾图形成过程进行描述，如式(1)所示：

I(x)=J(x)t(x)+A(1-t(x))

(1)

其中，I(x)为有雾图像；J(x)为无雾图像；A为大气光；t(x)为场景透射率，表示光线在传播过程中未被散射且到达成像设备的部分。当大气同质时，t(x)可表示为式(2)：

t(x)=e-βd(x),0≤t(x)≤1

(2)

其中，β为大气散射系数,d(x)为场景深度。基于物理模型去雾的关键在于通过估计未知参数A和t(x)，结合大气散射模型从I(x)中恢复出J(x)。显然该复原过程是一个典型的病态问题，因此需要借助一些先验知识或约束条件来达到图像去雾的目的。

2.2 暗通道先验理论

He等人[11]通过对大量户外无雾图像进行统计，得出在无雾图像非天空区域中至少存在一个颜色通道，其像素值很低甚至趋近于0，该通道称为暗通道，用公式可表示为如式(3)所示：

(3)

其中，Jdark(x)称为无雾图像暗通道，Ω(x)是以像素x为中心的邻域窗口，c表示r,g,b通道中的某个颜色通道。假设大气光A为常数，对式(1)两边同时作2次最小值运算可得到式(4)：

(4)

其中，Idark(x)表示有雾图像的暗通道。结合式(3)可得透射率表达式如式(5)所示：

(5)

由于暗通道采用了2次最小值滤波操作，导致恢复图像在景深突变处产生严重的光晕现象，为此He等人[11]引入Soft Matting方法对透射率进行优化,以获得较好的边缘保持特性，但其时间复杂度极高。后来，He等人[16]又提出使用引导滤波技术代替软抠图处理，算法效率得到了很好的提升。

3 本文算法

针对暗通道先验算法在天空等高亮区域透射率估计不准确，以及景深突变处易产生光晕效应等问题，本文提出了一种基于转换域和自适应伽马校正的图像去雾算法，算法流程如图1所示。第1部分是对透射率进行估计，首先，对大气散射模型两边作对数变换，提出一种对数域正相关关系，通过构造高斯函数对其进行拟合得到透射率的粗略估计；然后，将有雾图像转换至HSV色彩空间提取亮度分量，构造自适应伽马校正因子对粗级透射率进行修正，再使用交叉双边滤波得到优化透射率。第2部分是大气光估计，受到局部大气光探索方法的启示，本文分别采用2个不同尺寸的滤波核执行闭操作处理，然后求取二者算术平均值得到均衡后的闭操作结果，从而得到改进后的大气光A。最后，利用大气散射模型得到复原的无雾图像。

Figure 1 Flowchart of the proposed algorithm图1 本文算法流程图

3.1 对数域转换

假设大气光A已知，对式(1)进行变换可得式(6)：

(6)

由于有雾图像I(x)、透射率t(x)及无雾图像J(x)之间必然存在某种相关关系，因此为了便于分析各变量之间的相关性，可对式(6)两边作对数变换，将其转换至对数域实现变量分离，并结合式(5)，得到式(7)：

(7)

大气光A不影响式(7)两边变量之间的相关性，因此基于式(7)，本文提出了一种对数域正相关关系，如式(8)所示：

ln(1-J(x))∝{ln(1-I(x))-ln(1-Idark(x))}

(8)

其中，I(x)和Idark(x)均为已知量。为了方便推导可设定中间变量temp(x)，其表达式如式(9)所示：

temp(x)=ln(1-I(x))-ln(1-Idark(x))

(9)

将temp(x)从对数域转换至标准空间，结合式(8)得到标准域下的正相关关系，如式(10)所示：

1-J(x)∝etemp(x)

(10)

由于高斯函数具有较好的分布特性，并且可以通过调节方差使其函数形状可控[17]，因此本文提出采用均值为1，方差为σ2的高斯函数来拟合式(10)中的正相关关系，从而实现无雾图像的初始估计J0(x),如式(11)所示：

J0(x)=1-e-(1-etemp(x))2/σ2

(11)

Figure 2 Dehazing results with different values of σ图2 不同σ值时的最终复原结果

其中，σ为标准差，其取值大小会影响无雾图像的最终复原质量。图2为选取不同σ值时的最终复原结果对比。从图2b～图2e可以看出，当σ值较小时，复原图像较为自然，但仍有残雾存在；当σ值较大时，图像去雾比较彻底，但又会出现轻微的过饱和现象。通过对大量雾图进行仿真，实验得出当σ取0.6时图像去雾后的复原质量最佳。

上述基于有雾图像及其暗通道估计的初始无雾图像J0(x)存在严重的块状伪影及光晕现象，并不能作为最终的复原结果，此处仍然估计J0(x)的目的在于实现本文透射率的粗略估计。

3.2 粗级透射率

假设大气光A已知，对式(1)两边同时执行最小通道操作，得到最小通道大气散射模型，如式(12)所示：

(12)

对式(12)进行变形得到透射率，如式(13)所示：

(13)

(14)

其中，k为衰减系数，代表有雾图像与其最小通道之间的衰减程度。根据大气成像理论，无雾图像与其最小通道间存在同样的衰减关系，因此可通过该衰减系数对J0(x)作近似衰减，得到式(15)：

(15)

结合式(13)可以得到透射率的粗略估计，如式(16)所示：

(16)

3.3 自适应伽马校正

通过粗级透射率所复原的无雾图像在部分区域出现发黑现象，并且图像整体偏暗。为了克服上述不足，本文使用伽马校正技术对粗级透射率进行修正，如式(17)所示：

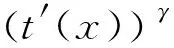
(17)

其中，γ为校正因子。当γ>1时，图像整体灰度值变小，即图像变暗；当γ<1时，图像整体灰度值变大，即图像变亮。为了避免透射率估计不足所引起的图像偏暗，设定γ的取值为[0,1]。然而，对于不同的有雾图像，需分别设置不同的γ值来使复原图像拥有最佳效果，这导致算法存在手动设置参数的缺陷。另外，在图像不同区域均采用所设定值对透射率进行修正，会使得部分区域透射率估计不准确，从而产生颜色失真现象。因此，本文提出采用亮度分量构造自适应伽马校正因子，实现在图像不同区域采用不同的γ值对粗级透射率进行校正，这不仅降低了算法复杂度，而且有效避免了部分区域颜色失真现象。首先，将有雾图像转换至HSV色彩空间以提取亮度分量v(x)，然后对其作如式(18)所示的处理，得到自适应伽马校正因子：

γ=1-α·v(x)

(18)

其中，α为控制参数，控制图像去雾程度，经验取值为0.4。结合式(17)和式(18)得到自适应伽马校正之后的透射率，再利用交叉双边滤波对其作平滑处理，得到优化透射率。

图3为粗级透射率校正前后复原结果对比图。图3b是透射率未校正之前所得的复原结果，可以看出图像中铁轨处发黑严重且复原结果整体偏暗；图3c为自适应伽马校正之后所得的复原结果，局部区域发黑现象明显得到抑制，且复原图像明亮度适宜，去雾效果较好。

Figure 3 Comparison of recovered results before and after transmission correction图3 透射率校正前后复原结果对比

3.4 大气光估计

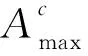
如图4所示，与Sun算法[18]相比，本文大气光估计更为准确且在局部区域内具有更多细节信息。同时，本文算法的复原结果亮度适宜，边缘处没有出现光晕现象，整体效果较好。

Figure 4 Comparison of atmospheric light and recovered results图4 大气光及复原结果对比

3.5图像复原

基于上述内容得出大气光A和优化透射率，将二者代入大气散射模型便可得到最终的复原图像J(x)，如式(19)所示：

(19)

其中，设定t0为透射率的下限值，取值为0.1，目的是为了避免分母趋于0。

4 实验结果与分析

为了验证所提算法的有效性与可行性，本文选取多幅雾霾天气图像进行对比实验，从主观评价和客观评价2方面对算法复原结果进行分析。

4.1 主观评价

主观评价是以人的主观感受为准，存在一定的片面性，但可以直观地反映出图像的复原效果。本文选取6幅具有不同特征的雾天图像作为实验样本，其中包括近景与远景区域、天空与非天空区域、薄雾与浓雾区域。基于这些图像将本文算法与文献[16]中的算法(简称He算法)、文献[12]中的算法(简称Meng算法)、文献[6]中的算法(简称Ren算法)、文献[7]中的算法(简称Li算法)和文献[8]中的算法(简称Qin算法)进行对比，实验结果如图5所示。

Figure 5 Comparison of experimental results图5 实验结果对比

图5a为输入的有雾图像。图5b为He算法中使用暗通道先验算法复原的结果，可以看到雾气基本去除，但在景深突变区域仍存在严重的光晕效应且去雾不够彻底，如第1和第6幅图像。另外，对于包含天空区域的图像透射率估计不准确，导致天空区域出现偏色现象，如第2和第3幅图像。图5c为Meng算法中使用的边界约束算法复原的结果，恢复图像细节明显增多但色彩保真度较差，出现了颜色失真及过饱和现象，尤其在天空及景深变化区域偏色严重，如第2、第3和第6幅图像。图5d为Ren算法中使用多尺度卷积神经网络算法复原的结果，对于薄雾图像去雾比较彻底，但在部分区域仍存在严重的偏色及过饱和现象，如第1和第2幅图像中的树叶和天空区域。图5e为Li算法中使用一体化去雾网络算法复原的结果，存在轻微的过饱和现象，且复原结果整体偏暗，因而视觉效果一般，如第1和第4幅图像。图5f为Qin算法中使用特征融合注意力网络算法复原的结果，恢复图像在天空区域具有较好的表现，但在景深突变处仍有轻微的光晕效应，如第1和第6幅图像。图5g为本文算法复原的结果，整体而言恢复图像去雾彻底，仅在极少区域有残雾现象，并且明亮度适宜，具有良好的色彩保真度。与其它几种算法相比，本文算法抑制了光晕效应及块状伪影的产生，同时能恢复出较多细节信息，如第4和第6幅图像，此外天空区域保持相对较好，没有出现颜色失真现象。

4.2 客观评价

为了使实验对比更加全面有效，本文采用Hautiere等人[20]提出的无参考图像质量评估方法，选取可见边集合数e、平均梯度r、峰值信噪比PSNR(Peak Signal-to-Noise Ratio)及运行时间t作为客观评价指标。其中，峰值信噪比是指有用信号与噪声之间的比值，e和r的值越大也说明算法的复原效果越好，其定义如式(20)和式(21)所示：

(20)

(21)

仍以图5中的6幅有雾图像作为实验样本，采用目前经典的图像去雾算法与本文算法进行客观对比，实验结果如图6所示。从图6a可以看出，相比于其他5种算法，本文算法在可见边指标上取得了最佳效果。图6b为平均梯度，本文算法的该指标性能明显优于He算法、Li算法及Qin算法，但与Meng算法相比略有不足。图6c为峰值信噪比，各算法在该指标上的性能差异不是很大，但整体而言本文算法表现较好。图6d为运行时间，本文算法虽不及He算法，但相比其他4种算法而言时间复杂度较低。综上，与其他经典算法相比，本文算法具有一定的优越性。

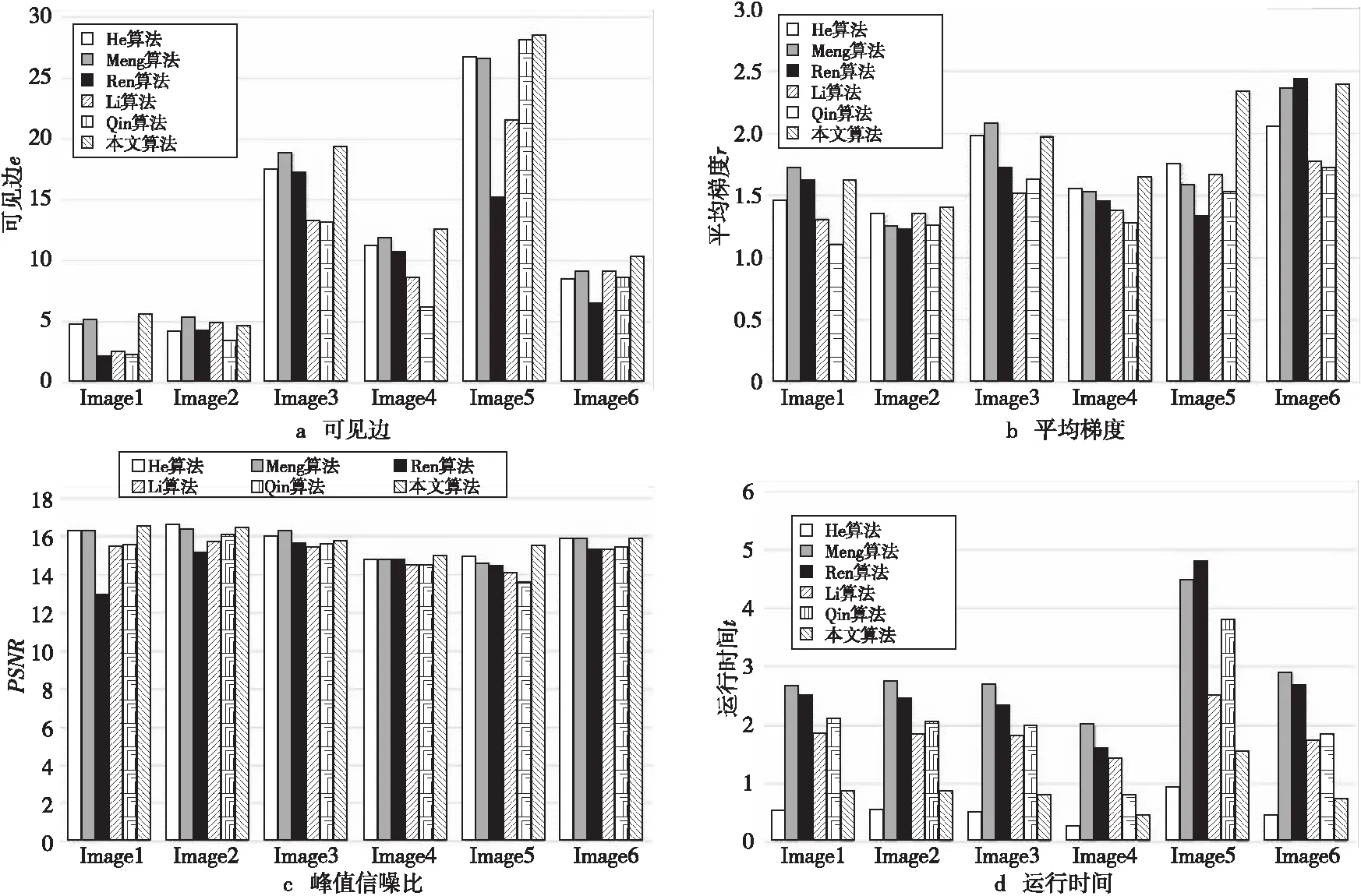
Figure 6 Objective evaluation图6 客观评价

Figure 7 Comparison of experimental results图7 实验结果对比

4.3 测试集验证

除了上述真实场景下的有雾图像对比实验，本文还在合成有雾图像数据集上进行了比较，以进一步验证所提算法的有效性。如图7所示，以随机选取的几幅合成图像作为实验样本，对各算法复原结果进行主观分析，可以看出本文算法在合成图像处理中同样具有较好的复原效果。其中，He算法及Meng算法恢复图像具有明显的过饱和现象，且天空区域偏色严重；Ren算法和Li算法天空区域复原效果自然，但部分区域存在去雾不彻底现象；Qin算法虽去雾彻底，但复原图像整体偏暗，相比之下，本文算法复原结果明亮度适宜，天空区域没有失真现象且整体去雾比较彻底。

在客观评价上，本文采用峰值信噪比PSNR和结构相似性SSIM(Structural SIMilarity)作为评价指标[21]。其中，结构相似性用来衡量2幅图像的相似度，值越大，代表算法性能越好。从表1可以看出，与其他算法相比，本文算法在PSNR指标上取得了最优效果，SSIM指标性能也相对较好，进一步证明了所提算法的有效性。

Table 1 PSNR and SSIM on synthetic hazy images

5 结束语

为了避免暗通道先验算法中存在的光晕效应以及天空等明亮区域颜色失真现象，本文提出了一种基于转换域与自适应伽马校正的图像去雾算法。将大气散射模型转换至对数域提出对数域正相关关系；然后采用高斯函数对其拟合得到粗级透射率，利用亮度分量构造自适应伽马校正因子对粗级透射率进行修正得到优化透射率，并结合改进后的局部大气光得到最终的复原图像。实验结果表明，本文算法复原图像去雾彻底且清晰自然，在保持较好色彩保真度的同时有效地抑制了天空区域偏色及光晕现象。但是，该算法在时间复杂度方面还略有不足，将作为下一步工作进行改进。