基于机器学习的电潜泵工况诊断
2022-09-21王彪韩国庆路鑫谭帅朱志勇梁星原
王彪 韩国庆 路鑫 谭帅 朱志勇 梁星原
中国石油大学(北京)石油工程教育部重点实验室
电参数能够反映电潜泵的实时工作状态,且容易实现监测和收集,因此在油田开发生产过程中,通过电参数对电潜泵的工作状况进行监测和分析的研究较多,常见的有电流卡片方法等。这些方法依赖人工经验,存在人为因素和主观误差。使用机器学习算法可以实现电参数的自动分析,提高效率并降低主观误差。陈治国等[1]提出了基于模式识别的电流卡片特征值的提取方法,给出了人工判断的量化指标;余继华等[2]引入了机器学习,采用神经网络方法识别电流工况,甘露等[3]使用BP算法对神经网络进行了进一步扩充;韩国庆等[4]补充了更多工况类别,进一步扩充了神经网络的适用性;Gupta等[5]使用主成分分析方法讨论了电潜泵工况偏离正常状态时的可视化构建和评判方法;王国辉等[6]基于主成分分析法讨论了电潜泵大数据综合分析预警系统的构建,提出通过对大数据降维实现油井状态描述和监控预警的方法;隋先富等[7]基于主成分分析法,对电潜泵的多维参数进行降维,通过多维参数监测了电潜泵的工作状态改变。前人的研究侧重于通过某一种方法对电潜泵井的生产状态进行描述,认识不断加深,但缺乏从特征提取及处理然后进行分类识别并综合评价的机器学习完整流程,在不同环节中依然保留有人为因素。本研究在前人研究基础上,构建了机器学习的完整流程,通过特征工程对波动的电流数据提取大量的特征信息,然后通过降维算法实现特征描述和可视化,再通过分类算法实现工况诊断并给出具体结论,最后进行分析与评价。使用实际生产时的电流数据实例,通过以上4个部分的流程的综合,实现了对电潜泵工况的快速准确且直观的描述。
1 电流卡片诊断方法及其改进
电流卡片诊断是API于1982年提出的一种电潜泵故障分类方法,其分类的依据是在不同的工况下运行的电潜泵具有不同的电流波动特征[3],例如波动的时间长短、波动的频次大小、电流的峰值与额定值之间的关系等。传统方法受限于技术条件,通过形态来进行模糊识别,具有较强的主观因素,在泵工况识别过程中会导致人为误差[8]。
为了减少误差,学界进行了多方面的研究,各种传感器和数据记录设备的发展,也大大方便了电流参数的量化。传统的电流卡片记录分钟级的电流平均数据,常见的有6 min一个点[9]。随着传感设备和数据记录设备的性能提升,当前油田生产中得到的电流数据可以达到20 s一个点甚至更密。数据记录密度的提升使得电流记录可以体现出有关电泵工作状况的更多信息。此时通过传统的对电泵工作状况改变导致电流波动的机理分析就显得不够精细和迅速。
数据密度的提升带来了更多的电流特征。对于分析而言,这些特征的保留使得挖掘更多的信息成为可能。而采用传统的方法识别,会忽视掉这些特征的细节,这种信息丢失给工况的识别带来了误差。经过稀释的数据可能会淹没一些关键的波动信息,使得一些原本正常的波动变成没有规律的波动,导致局部的信息丢失和整体的信息变异,其中信息丢失是指局部位置的波动峰值或波动周期的消失,信息变异是指整体的波动形态的改变。此外由于稀释算法导致的信息损失,可能使得一些原本存在差异的电流波动图形变得接近,失去其独特性,从而导致不同工况的电流数据被诊断为同一种工况,影响判断的准确性。
为了详细说明局部的信息丢失与整体的信息变异,选取一口气体影响工况井的20 s一个点的高密度实际电流数据,从中取30 min数据作为研究对象,放大并与一种稀释算法和一种间歇采样方法获得的6 min一个点的稀释数据进行特征对比。由图1可看出,高密度实时电流数据反映了某种规律的电流波动,可能与负载的工作情况有关。然而通过传统的均值方法或间歇采样得到的低密度电流数据中产生了相比于原始数据的信息丢失,可能导致生产中的某些关键信息的损失。

图1 电潜泵气体影响工况的高密度实时电流数据与稀释的电流数据特征对比Fig.1 Feature comparison of high-density real-time current data and diluted current data of ESP under the working condition of gas influence
解决此类信息损失的方法是尽可能保留传感器设备传输的原始密度的数据并进行计算和分析,使用合理的方法去除其中包含的噪声,同时减少对原始数据的伤害,而非使用其他方法将数据直接稀释后计算。对于大量数据的处理与分析可以通过使用机器学习方法完成,以实现又快又好的评判效果。
2 机器学习流程
基于电潜泵电流数据的工况识别需要进行包括数据预处理、特征提取、特征降维、分类模型的训练及预测等流程,方法如图2所示。

图2 基于电潜泵电流数据的工况识别流程图Fig.2 Flow chart of working condition recognition with ESP current data
为了减少数据稀释带来的信息损失,需要尽量保留原始的数据密度进行运算。然而更大的数据量导致了计算的困难,也给问题的分析带来了挑战,因此需要实施特征工程从原始的波动信息中提取出关键的有效信息。
2.1 特征工程
特征工程是指将原始数据转化为更好地表达问题本质特征的过程,将这些特征运用到预测模型中,能提高对不可见数据的模型预测精度。特征工程的目标是找到分解和聚合原始数据,以更好地表达问题本质的方法,即发现对因变量y有明显影响作用的自变量特征x。因此,特征工程是数据挖掘模型开发的基础。
归一化过程是对原始数据进行线性变化,使结果落到[0,1]区间,以便消除不同数据量级之间的差别,减少分析误差,转换函数为

在电潜泵电流分析及工况诊断中,对电流的归一化数据进行波形分析,得到时域特征和波形特征作为模型的输入,具体方法如下。
2.1.1 时域特征
(1)特征值1:方差,当前电流值和电流均值之间的偏离程度的度量,定义为

(2)特征值2:均方根值,当一组数据中存在较多0值,即占空比较高时,直接计算其均值不能反映电流强度有效值,均方根值则可以很好地表征电流强度有效值[10],定义为

(3)特征值3:方根幅值,对振幅的变化非常敏感的物理量[11],定义为

式中,Ivar为电流方差,A;Ii为当前电流,A;I为电流均值,A;Irms为电流均方根,A;Ir为电流方根幅值,A。
2.1.2 波形特征
(1)特征值4:峰值因数,表示电源系统能够提供峰值电流能力的指标要求[12],定义为

(2)特征值5:偏度因子,数据分布偏斜方向和程度的度量,是数据分布非对称程度的数字特征[13],负偏度代表统计数据为右偏分布,正偏度代表统计数据为左偏分布,定义为

式中,Cf为峰值因数;Imax为电流最大值,A;Sk为偏度因子。
(3)特征值6:波形因子,用于量化表征波形偏离正弦波形的程度[14],定义为

其中

(4)特征值7:脉冲因子,用于描述信号冲击的指标[15],定义为

(5)特征值8:裕度因子,用来检测信号中有无冲击的指标,常用于监测机械设备的磨损状况[16],定义为

(6)特征值9:峭度,是反映随机变量分布特性的数值统计量,可以在频域内表示一系列瞬态的存在及其位置,消除非平稳信号[17]。定义为

(7)特征值10:峭度因子,表示波形平缓程度,用于描述对振动信号冲击特性的反映[18],定义为

式中,Sf为波形因子;Iarv为整流平均值,A;Ii(t)为随时间变化的电流值,A;Cif为脉冲因子;Cmf为裕度因子;Ck为峭度;Ckf为峭度因子。
通过以上方法对波动的电流数据实施特征工程,即可将波动电流中包含的特征信息尽可能地挖掘出来,以便实施后续的机器学习步骤。特征工程是升维过程,从一维连续时间内的波动中提取出多维特征信息,然后针对这些特征信息展开分析,以数学模型来表达,在特征工程实现过程中提取出的多变量大数据集为研究和应用提供了丰富信息。
2.2 数据降维的聚类算法
在特征工程实现了数据特征的挖掘之后,需要根据挖掘得到的特征值进行处理与分析,处理的过程主要使用聚类算法实现数据降维,以降低计算复杂度。如果采用单独对每个特征值进行分析的低维度分析方法,则分析往往是孤立的,不能实现数据中信息的综合利用,盲目减少分析的特征值会损失很多有用的信息,从而给分析带来误差。因此需要找到一种合理的方法,在减少需要分析的特征值的同时,尽量减少特征值中所包含信息的损失,以实现对所收集数据的全面分析。常用的数据降维方法有很多,本文采用主成分分析法(PCA)去除数据中的噪声,降低算法的计算开销,使得结果更容易可视化并为人所理解[19]。使用主成分分析进行降维是通过线性变化将原始数据变换为一组各维度线性无关的标识,提取数据的主要特征分量。使用主成分分析方法降维可以获得各主成分的变异系数,将这些变异系数按照主成分绘制为柱状图,即为PCA的碎石图,反映降维后的各主成分所保留的原始信息的百分比。根据可接受的保留信息的比率,通过碎石图的累积值可以帮助确定所需达到的维度。
降维的维度确定后,就可以将原本多维空间中的点投射到降维形成的主成分空间中,观察参数的聚集情况。通过对原本数据的所属工况打上颜色标签,可以直观地观察各工况在主成分空间中是否存在特殊的聚集关系,实现聚类结果的可视化。通过对该聚集关系的描述,就可以进行机器学习的下一步流程,建立实现分类任务的机器学习模型。
2.3 基于逻辑回归算法(LR)的模式识别
在完成参数的降维、聚类与可视化后,使用分类算法对本研究中的数据聚集情况进行具体的划分。逻辑回归是当前业界比较常用的机器学习方法,用于估计某种事物的可能性[20]。它与多元线性回归同属一族,即广义线性模型。多元线性回归是直接将特征值和其对应的概率相乘得到一个结果,逻辑回归是在这个结果上加一个逻辑函数,来实现对于事物属于某一类别的可能性估计。逻辑回归的主要思想是在模型训练中,首先得到极大似然函数,然后使用梯度下降法求解函数中参数的近似值。
使用逻辑回归模型根据一个特征值进行二分类问题求解时,由坐标(x,y)确定的每个点代表一个样本,其中y值的0和1代表两种样本标签,x代表样本特征。在分类模型训练过程中,通过采用不同函数对训练样本进行拟合,回归出一个能够描述大多样本特征的函数,该函数就是最终确定的分类模型。对于本任务的多分类回归问题,使用逻辑回归模型可以将一个n分类任务拆分为n个二分类任务。某个分类任务归属于某种类型,则该类型i对应的第i个混淆特征即为1,其余混淆特征为0,通过对每个混淆特征进行二分类,从而实现多分类。
2.4 机器学习算法的评估方法
在多分类任务完成后,对机器学习算法得到的结果评估是机器学习算法完成后的必要流程。对于多分类任务的评估指标包括准确率(Accuracy)、精确率 (Precision)、召回率 (Recall)、和F1分数 (F1-Score)方法等。根据所要处理的问题不同,各种评估指标具有不同的适用性。
准确率是指对于给定的测试数据集,分类器正确分类的样本数与总样本数之比[21]。但当分类任务中不同类型的样本数量差异比较大时,或者分类任务目标不同,准确率未必能够真实地反映分类器的分类效果。为了弥补准确率方面的不足,引入了精确率、召回率和F1分数的概念。以二分类任务为例,定义4种分类状况:真正类(True Positive)、假正类 (False Positive)、假负类 (False Negative)、真负类(True Negative)。
通过以上4种概念定义精确率和召回率。精确
率表示分类器预测为正的样本中有多少个是真实的正样本,召回率表示样本中的正例有多少被正确预测了,两者分别评判了分类器的漏报或误报率。精确率和召回率之间是互相影响的,对于一个案例而言,最好的情况是做到两者都高,但一般情况下精确率高、召回率就低,召回率高、精确率就低。
对于电潜泵的故障诊断而言,既希望召回率高,即减少漏报,避免额外的经济损失,又希望精确率高,即减少误报,避免额外的工作量和人力物力投入。因此,精确率和召回率之间还需要一定的平衡。此时就可以使用F1分数来对两者进行均衡,精确率和召回率越高,则F1分数越高,分类任务越好。
3 案例分析与评价
从A油田电潜泵井数据库中提取了正常工况、泵抽空、过载停泵、频繁短周期运行4种工况的井共计56口,使用前文所述特征工程的方法从56口井的实时电流数据中分别提取10个特征值。各样本井的特征值与工况的对应关系部分示例见表1。

表1 样本的特征值与工况对应关系的部分示例Table 1 A partial example of the correspondence between eigenvalues and working conditions of samples
利用基于皮尔逊相关系数的相关性分析法对这10个特征值和实际工况进行相关性描述,线性正相关性越强,则相关度越接近1,线性负相关性强,则相关度越接近−1。从图3各特征值之间的相关关系,以及各特征值与最终工况的相关关系量化可以直观看出,部分特征值之间存在较强的线性相关性,这说明部分特征值表现的特征是重复的,可以进行适当的降维操作以提取出主要的特征描述方法,降低机器学习的计算量和计算复杂度。且从与工况的关系也可以看出,工况与各个特征值之间均存在较强相关性,这也说明,仅使用单个特征值难以描述对结果的影响。

图3 各特征值和工况彼此之间的相关系数Fig.3 Correlation coefficients of eigenvalues and the working conditions with each other
基于相关性热力图得到的分析结果,其中存在的线性相关性较强的变量需要进行降维以降低计算量并实现可视化。对这些特征值去除工况结论进行无监督的PCA降维聚类,图4的PCA碎石图展示了降维的主成分数量保留原始信息的程度,以各主成分解释的方差比进行量化。
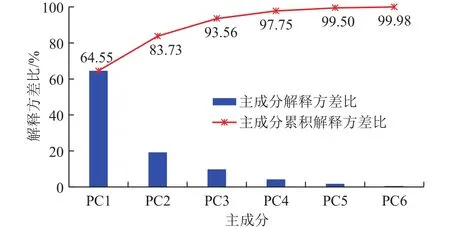
图4 使用PCA降维的碎石图和累积分布图Fig.4 Scree plot and cumulative distribution diagram obtained from dimensionality reduction with PCA
从图4可以看出,PC1对电流特征值所包含信息的保留程度达到64.55%,PC2对电流特征值所包含信息的保留程度达到19.18%,PC1和PC2共同达到的信息保留程度达到83.73%。两个主成分就可以保留80%以上的特征值信息,因此从可视化效果以及计算难度上考虑,可以认为使用两个主成分即可实现对电流特征值的总体描述。
使用降维后的特征值进行二维无监督聚类,观察数据的聚类情况,以便确定使用电流特征值的二维聚类判别电泵工况的实现可行性。二维无监督聚类效果如图5所示。

图5 对电参数特征值进行二维无监督聚类的结果Fig.5 The results of 2-dimensional unsupervised clustering for the eigenvalues of current data
从图5可以看出,上述56口井在主成分分析图中似乎有3到4处较好的聚类。为了确定这种聚类方式是否与各个工况相关,用原本各个电流情况对应的工况作标签来对各聚类点进行颜色和形状的标记,结果如图6所示。

图6 PCA聚类中各点所代表的工况情况Fig.6 The working conditions represented by points in the clustering diagram with PCA
从图6可以看出,电潜泵的电参数特征值进行二维无监督聚类的位置分布情况确实与不同工况有关,因此认为此次聚类效果较好,实现了各个工况的特征分离。从PCA降维的碎石图上看,6个维度的主成分能够描述电流的几乎99.98%的信息。因此根据PCA算法,形成特征值与主成分的系数矩阵热力图,如图7所示。

图7 各特征值与各主成分之间的相关系数Fig.7 Correlation coefficients of each eigenvalue with each principal component
图7中6个主成分与10个特征值的关系的描述为:每一行对应一个主成分,每一列对应一个特征值。以第1行为例,表明第1主成分可使用该行中每格的权重数值与其对应的特征值乘积的累加和表示如下

式中,f1~f10分别表示特征值1至特征值10。
其他主成分的表示方式与第1主成分的表示方式类似。
对主成分与特征值之间关系描述的主要作用是,当新输入一口井的数据并提取特征值后,按照热力图中每个点的系数,即可求取各个主成分值,以便进行后续的机器学习算法。
从图6的工况分布情况来看,PCA聚类在描述各个电泵工况时具有较好的能力,对于新加入的一口井的数据而言,如果提取特征值并降维后分布位置在上述聚簇内部,那么该井所处工况属于该聚簇表示的工况的可能性较大,但如果新加入的一口井处于某两种工况形成的聚簇之间时,对于工况的判别就难以直接描述。此时需要对数据进行机器学习完成分类任务,以进行工况的准确识别和判断,最终实现机器学习的数据处理、训练与预测的闭环。
使用逻辑回归方法对4种工况类型的56口样本井的数据进行学习和预测,测试集占比设置为30%,计算得到准确率0.84,精确率、召回率和F1分数见表2。

表2 使用逻辑回归的机器学习的结果评价Table 2 Results evaluation of ML using LR algorithm
如表2所示,模型最终实现的效果中,4种工况类型的56口井的各评价指标评价结果均达到80%以上,且平均F1分数达到了85%,说明使用电流特征值降维的二维主成分建立的逻辑回归模型在这4种工况类型的56口电泵井的评价中实现了较好的分类效果。
4 结论
(1)与传统的电流特征识别方法相比,基于机器学习的电潜泵电流分析及工况诊断实现了对电流数据的特征提取,将电流波动的形状描述问题转化为基于数据的数学特征量化描述问题,提升了评价的客观性,减少了人为误差。
(2)通过特征工程提取的特征值本身复杂多样,且各个特征值之间可能具有较强的线性相关性,需要对这些数据剔除线性相关变量,保留线性无关变量,以便减少机器学习的输入数据,降低机器学习的模型复杂度。采用PCA方法降维,一方面保留了特征提取中获得的主要特征,另一方面减少了机器学习的输入数据维度,降低了计算复杂度,同时还能通过聚类效果的可视化确定数据特征提取是否满足泵工况描述的要求。使用二维主成分表征的电潜泵工况信息保留程度达到83.73%,降维聚类表现出了良好的工况区分性,为使用逻辑回归方法实施分类任务奠定了基础。
(3)使用降维后的电参数特征数据,建立逻辑回归模型,完成了对电潜泵工况的诊断。对4种工况类型的56口电潜泵井的诊断准确度、精确度、召回率均达到了80%以上,F1分数达到了平均85%的水平,达到了期望的分类识别效果,实现了有效的电潜泵工况诊断。
